LeetCode-994. 腐烂的橘子【广度优先搜索 数组 矩阵】

题目描述：

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

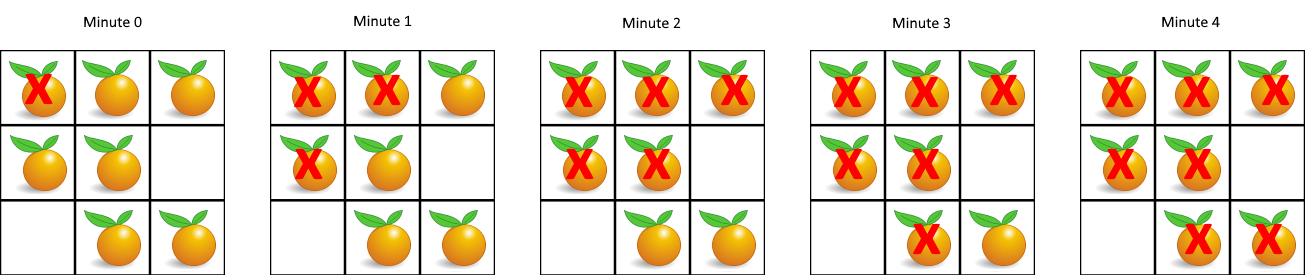
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2

解题思路一：多源广度优先搜索（队列实现）

观察到对于所有的腐烂橘子，其实它们在广度优先搜索上是等价于同一层的节点的。

假设这些腐烂橘子刚开始是新鲜的，而有一个腐烂橘子(我们令其为超级源点)会在下一秒把这些橘子都变腐烂，而这个腐烂橘子刚开始在的时间是 −1 ，那么按照广度优先搜索的算法，下一分钟也就是第 0 分钟的时候，这个腐烂橘子会把它们都变成腐烂橘子，然后继续向外拓展，所以其实这些腐烂橘子是同一层的节点。那么在广度优先搜索的时候，我们将这些腐烂橘子都放进队列里进行广度优先搜索即可，最后每个新鲜橘子被腐烂的最短时间 dis[x][y] 其实是以这个超级源点的腐烂橘子为起点的广度优先搜索得到的结果。

为了确认是否所有新鲜橘子都被腐烂，可以记录一个变量 cnt 表示当前网格中的新鲜橘子数，广度优先搜索的时候如果有新鲜橘子被腐烂，则 cnt-=1 ，最后搜索结束时如果 cntcntcnt 大于 0 ，说明有新鲜橘子没被腐烂，返回 −1 ，否则返回所有新鲜橘子被腐烂的时间的最大值即可，也可以在广度优先搜索的过程中把已腐烂的新鲜橘子的值由 1 改为 2，最后看网格中是否由值为 1 即新鲜的橘子即可。

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        time = 0
        dirs = [[-1, 0], [0, 1], [1, 0], [0, -1]]
        queue = deque()
        # add the rotten orange to the queue
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 2:
                    queue.append((i, j, time))
        # bfs
        while queue:
            x, y, time = queue.popleft()
            for d in dirs:
                nextx = x + d[0]
                nexty = y + d[1]
                if nextx < 0 or nextx >= m or nexty < 0 or nexty >= n:
                    continue
                if grid[nextx][nexty] == 1:
                    grid[nextx][nexty] = 2
                    queue.append((nextx, nexty, time + 1))

        # if there are still fresh oranges, return -1
        for row in grid:
            if 1 in row: return -1
        return time
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

时间复杂度：O(nm)
空间复杂度：O(nm)

解题思路二：哈希表实现，先找出所有腐烂和新鲜橘子的集合{}类似于set()。每剔除一次time+=1

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        row = len(grid)
        col = len(grid[0])
        rotten = {(i, j) for i in range(row) for j in range(col) if grid[i][j] == 2} # 腐烂集合
        fresh = {(i, j) for i in range(row) for j in range(col) if grid[i][j] == 1}  # 新鲜集合
        time = 0
        while fresh:
            if not rotten: return -1
            rotten = {(i + di, j + dj) for i, j in rotten for di, dj in [(0, 1), (0, -1), (1, 0), (-1, 0)] if (i + di, j + dj) in fresh} # 即将腐烂的如果在新鲜的集合中，就将它腐烂
            fresh -= rotten # 剔除腐烂的
            time += 1
        return time
1
2
3
4
5
6
7
8
9
10
11
12
13

时间复杂度：O(nm)
空间复杂度：O(nm)

解题思路三：0

1

时间复杂度：O(n)
空间复杂度：O(n)