看看去年蓝桥考了什么，第十三届蓝桥杯省赛（C/C++ 大学B组）题解_对于 100100 的数据,1≤a,b≤1061≤a,b≤106。

A：九进制转十进制

问题描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

九进制正整数 (2022)9 转换成十进制等于多少？

运行限制

最大运行时间：1s
最大运行内存: 512M

题目思路

这是一道经典的进制转换题目，具体可以点进链接看看这篇文章。进制转换点击这里！！！

代码演示

#include <bits/stdc++.h>
using namespace std;
int main()    
{
	string s ="2022";
	int ans = 0;
	for(int i = 0; i < s.size(); i++) {
		char t = s[i];
		if(t >= '0' && t <= '9') 
			ans = ans * 9 + t - '0';
		else 
			ans = ans * 9 + t - 'a' + 10;
	}
	cout<< ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

B：顺子日期

问题描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

小明特别喜欢顺子。顺子指的就是连续的三个数字：123、456 等。顺子日期指的就是在日期的 yyyymmdd 表示法中，存在任意连续的三位数是一个顺子的日期。

例如 20220123 就是一个顺子日期，因为它出现了一个顺子：123； 而 20221023 则不是一个顺子日期，它一个顺子也没有。

小明想知道在整个 2022 年份中，一共有多少个顺子日期?

运行限制

最大运行时间：1s
最大运行内存: 512M

题目思路

这道题题目很坑，其实含有012的日期也是一个顺子日期。
我们用数组表示日期，遍历每一个月日，当符合顺子日期的定义时，记录一次答案。

代码演示

#include <bits/stdc++.h>
using namespace std;
int date[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};   
int main()
{
    int b[8] = {2,0,2,2};                              
    int sum = 0;
    for (int i = 1; i <= 12; i++) {
        b[4] = i / 10;                
        b[5] = i % 10;               
        for (int j = 1; j <= date[i]; j++) {
            b[6] = j / 10;            
            b[7] = j % 10;          
            if ((b[4] + 1 == b[5] && b[5] + 1 == b[6]) || (b[5] + 1 == b[6] && b[6] + 1 == b[7])) 
                sum++;
            }
        }
    }
    cout << sum << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

C：刷题统计

问题描述

小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天 做 a 道题目, 周六和周日每天做 b 道题目。请你帮小明计算, 按照计划他将在 第几天实现做题数大于等于 n 题?
输入格式

输入一行包含三个整数 a,b 和 n.
输出格式

输出一个整数代表天数。
样例输入

10 20 99
1

样例输出

8
1

评测用例规模与约定

对于 50%50% 的评测用例, 1≤a,b,n≤1061≤a,b,n≤106.

对于 100%100% 的评测用例, 1≤a,b,n≤10181≤a,b,n≤1018.

运行限制

最大运行时间：1s
最大运行内存: 256M

题目思路

先计算出一周刷的题目数量，再计算出剩余题量需要几天。

代码演示

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

ll a,b,n,add,day;
int main() {
	cin >> a >> b >> n;
	int ti = 5 * a + 2 * b;
	ll weak = n / ti;
	ll last = n % ti;
	day += weak * 7;
	int x = 1;
	while(last > 0) {
		if(x % 7 == 6 || x % 7 == 0) {
			last -= b;
		} else {
			last -= a;
		}
		day++;
		x++;
	}
	cout << day;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

D：修剪灌木

问题描述

爱丽丝要完成一项修剪灌木的工作。

有 N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晩会修剪一棵灌 木, 让灌木的高度变为 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始, 每天向右修剪一棵灌木。当修剪了最右侧的灌木后, 她会调转方向, 下一天开 始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。

灌木每天从早上到傍晩会长高 1 厘米, 而其余时间不会长高。在第一天的 早晨, 所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
输入格式

一个正整数 N, 含义如题面所述。
输出格式

输出 N 行, 每行一个整数, 第 i 行表示从左到右第 i 棵树最高能长到多高。
样例输入

3
1

样例输出

4
2
4
1
2
3

评测用例规模与约定

对于 30%30% 的数据, N≤10N≤10.

对于 100%100% 的数据, 1<N≤100001<N≤10000.

运行限制

最大运行时间：1s
最大运行内存: 512M

题目思路

对于左边的灌木来说，长的最高的时候应该是从自己出发向右走再返回自己的长度。
对于正中间的灌木来说，长度最高的时候就是从自己出发再返回。
对于右边的灌木来说，长的最高的时候应该是从自己出发向左走再返回自己的长度。

代码演示

#include <bits/stdc++.h>
using namespace std;

int n;

int main() {
    cin >> n;
    for(int i = 1; i <= n / 2; i++) {
        cout << 2 * n - 2 * i << endl;
    }
    if(n % 2 != 0) {
        cout << n - 1 << endl;
    }
    for (int i = n / 2; i > 0; i--) {
        cout << 2 * n - 2 * i << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

E：X 进制减法

问题描述

进制规定了数字在数位上逢几进一。

X 进制是一种很神奇的进制, 因为其每一数位的进制并不固定！例如说某 种 X 进制数, 最低数位为二进制, 第二数位为十进制, 第三数位为八进制, 则 X 进制数 321 转换为十进制数为 65 。

现在有两个 X 进制表示的整数 A 和 B, 但是其具体每一数位的进制还不确 定, 只知道 A 和 B 是同一进制规则, 且每一数位最高为 N 进制, 最低为二进 制。请你算出 A−B 的结果最小可能是多少。

请注意, 你需要保证 A 和 B 在 X 进制下都是合法的, 即每一数位上的数 字要小于其进制。
输入格式

第一行一个正整数 N, 含义如题面所述。

第二行一个正整数 Ma​, 表示 X 进制数 A 的位数。

第三行 Ma​ 个用空格分开的整数, 表示 X 进制数 A 按从高位到低位顺序各 个数位上的数字在十进制下的表示。

第四行一个正整数 Mb​, 表示 X 进制数 B 的位数。

第五行 Mb​ 个用空格分开的整数, 表示 X 进制数 B 按从高位到低位顺序各 个数位上的数字在十进制下的表示。

请注意, 输入中的所有数字都是十进制的。
输出格式

输出一行一个整数, 表示 X 进制数 A−B 的结果的最小可能值转换为十进 制后再模 1000000007 的结果。
样例输入

11
3
10 4 0
3
1 2 0
1
2
3
4
5

样例输出

94
1

样例说明

当进制为: 最低位 2 进制, 第二数位 5 进制, 第三数位 11 进制时, 减法 得到的差最小。此时 A 在十进制下是 108,B 在十进制下是 14 , 差值是 94。
评测用例规模与约定

对于 30% 的数据, N≤10;Ma,Mb≤8.

对于 100% 的数据, 2≤N≤1000;1≤Ma,Mb≤100000;A≥B.

运行限制

最大运行时间：1s
最大运行内存: 256M

题目思路

首先倒叙存储二进制整数A与B，按照贪心思想，当进制最小时为A-B的最小值，最小进制为max(a[i],b[i]) + 1,若进制比二小则为二进制。获得进制后直接计算十进制数字。

代码演示

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

int n,ma,mb,sa,sb,a[100005],b[100005];
ll ans;
int main() {
    cin >> n >> ma;
    for(int i = ma; i > 0; i--) {
    	cin >> a[i];
	}
	cin >> mb;
	for(int i = mb; i > 0; i--) {
		cin >> b[i];
	}
	int len = max(ma,mb);
	for(int i = len; i > 0 ;i --) {
		int c = max(a[i],b[i]) + 1;
		c = max(2,c);
		ans = (ans * c + a[i] - b[i]) % 1000000007;
	}
	cout << ans ;
    return 0; 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

F：统计子矩阵

问题描述

给定一个 N×M 的矩阵 A, 请你统计有多少个子矩阵 (最小 1×1, 最大 N×M) 满足子矩阵中所有数的和不超过给定的整数 KK ?
输入格式

第一行包含三个整数 N,M 和 K.

之后 N 行每行包含 M 个整数, 代表矩阵 A.
输出格式

一个整数代表答案。
样例输入

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
1
2
3
4

样例输出

19
1

样例说明

满足条件的子矩阵一共有 19 , 包含:

大小为 1×1 的有 10 个。

大小为 1×2 的有 3 个。

大小为 1×3 的有 2 个。

大小为 1×4 的有 1 个。

大小为 2×1 的有 3 个。

评测用例规模与约定

对于 30% 的数据, N,M≤20.

对于 70% 的数据, N,M≤100.

对于 100% 的数据, 1≤N,M≤500;0≤Aij≤1000;1≤K≤250000000

运行限制

最大运行时间：1s
最大运行内存: 256M

题目思路

先用二维前缀和存储矩阵信息，再用双指针来寻找正确答案。用i j分别表示一个区域的左右边界，p q来表示上下两个指针，p从上往下寻找q，一直到大小小于等于k，这时p q这片区域的行数q - p + 1就是子矩阵的个数。

代码演示

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

int n,m,k,a[505][505];
ll ans = 0;
int main() {
	cin >> n >> m >> k;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			cin >> a[i][j];
			a[i][j] =  a[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
		}
	}
    for(int i = 1; i <= m; i++) {
    	for(int j = i; j <= m; j++) {
    		for(int p = 1,q = 1; q <= n; q++) {
    			while(p <= q && a[q][j] - a[q][i - 1] - a[p - 1][j] + a[p - 1][i - 1] > k) {
    				p++;
				}
				if(p <= q) {
					ans +=(q - p + 1);
				}
			}
		}
	}
    cout << ans;
	return 0;
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

G：积木画

问题描述

小明最近迷上了积木画, 有这么两种类型的积木, 分别为 II 型（大小为 2 个单位面积) 和 LL 型 (大小为 3 个单位面积):

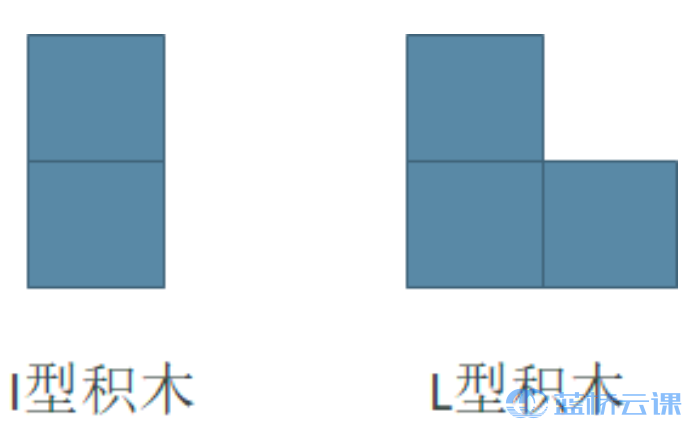
同时, 小明有一块面积大小为 2×N 的画布, 画布由 2×N 个 1×1 区域构 成。小明需要用以上两种积木将画布拼满, 他想知道总共有多少种不同的方式? 积木可以任意旋转, 且画布的方向固定。
输入格式

输入一个整数 N，表示画布大小。
输出格式

输出一个整数表示答案。由于答案可能很大，所以输出其对 1000000007 取模后的值。
样例输入

3
1

样例输出

5
1

样例说明

五种情况如下图所示，颜色只是为了标识不同的积木：

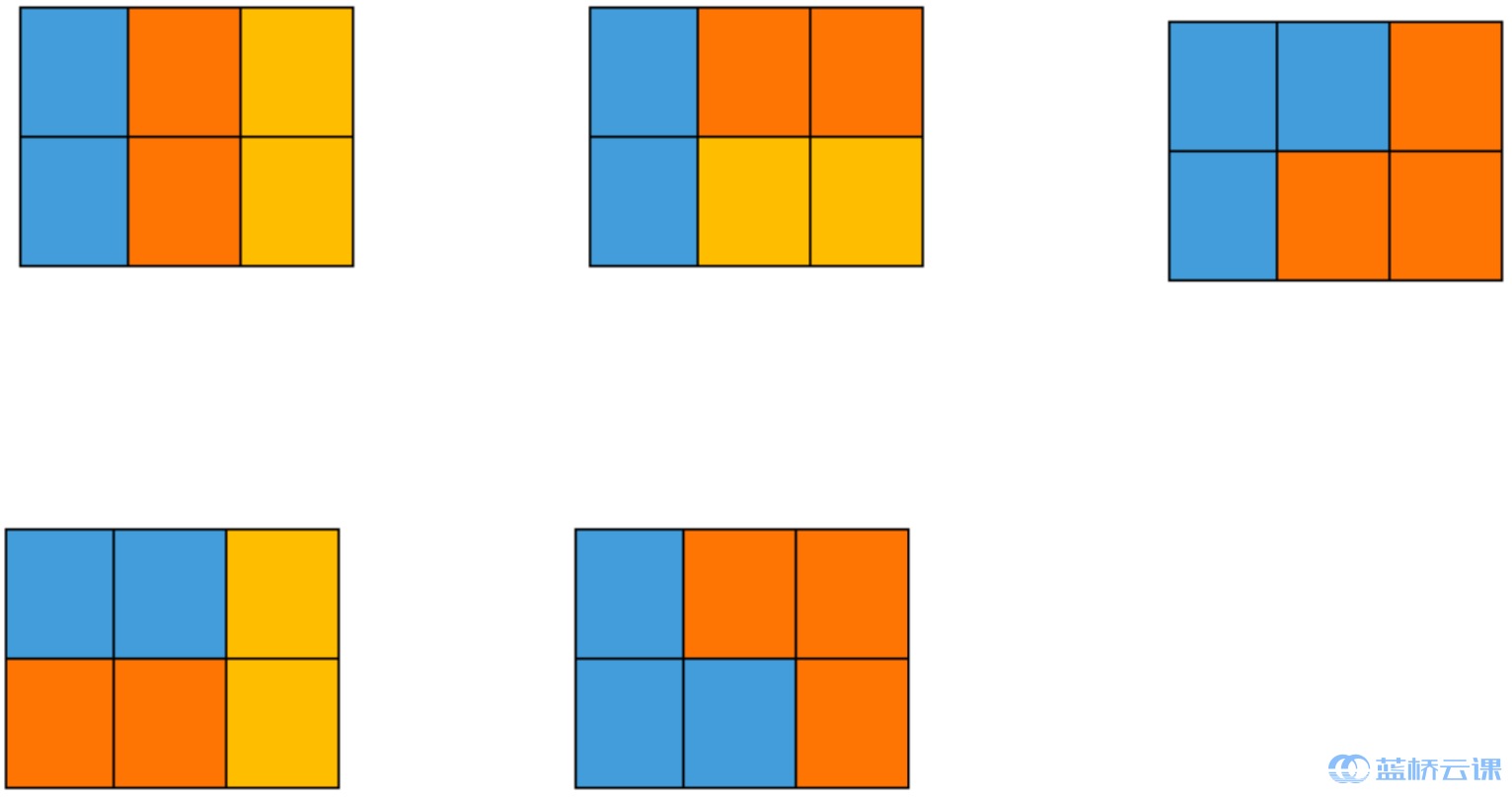
评测用例规模与约定

对于所有测试用例，1≤N≤10000000

题目思路

dp 题目，一共有三种情况，我们把1设为上层不为空，2设为下层不为空，3设成全不为空：

• 1：f[i][1]，这种情况为 f[i] 的上层不为空，可以通过 f[i - 1] 下层不为空和 f[i - 2] 全不为空得来。
• 2：f[i][2]，这种情况为 f[i] 的下层不为空，可以通过 f[i - 1] 上层不为空和 f[i - 2] 全不为空得来。
• 3：f[i][3]，这种情况为 f[i] 的上下层不为空，可以通过 f[i - 1] 上层不为空和 f[i - 1] 全不为空和 f[i - 1]下层不为空和 f[i - 2] 全不为空得来。
  最后输出 f[n] 全不为空就是答案。

代码演示

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
int n, m;
int f[10000005][4];

int main()
{
    cin >> n;
    f[0][3] = 1;
    for (int i = 1; i <= n; i++) {
        f[i][1] = (f[i - 1][2] + f[i - 2][3]) % mod;
        f[i][2] = (f[i - 1][1] + f[i - 2][3]) % mod;
        f[i][3] = ((f[i - 1][3] + f[i - 1][1]) % mod + (f[i - 1][2] + f[i - 2][3]) % mod) % mod;
    }
    cout << f[n][3] % mod;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

H：扫雷

问题描述

小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下, 在一个二维平面上放置着 n 个炸雷, 第 i 个炸雷 (xi,yi,ri) 表示在坐标(xi​,yi​) 处 存在一个炸雷, 它的爆炸范围是以半径为 ri​ 的一个圆。

为了顺利通过这片土地, 需要玩家进行排雷。玩家可以发射 m 个排雷火 箭, 小明已经规划好了每个排雷火箭的发射方向, 第 j 个排雷火箭 (xj,yj,rj) 表 示这个排雷火箭将会在 (xj​,yj​) 处爆炸, 它的爆炸范围是以半径为 rj​ 的一个圆, 在其爆炸范围内的炸雷会被引爆。同时, 当炸雷被引爆时, 在其爆炸范围内的 炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?

你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个 炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
输入格式

输入的第一行包含两个整数 n、m.

接下来的 n 行, 每行三个整数 xi​,yi​,ri​, 表示一个炸雷的信息。

再接下来的 m 行, 每行三个整数 xj​,yj​,rj​, 表示一个排雷火箭的信息。
输出格式

输出一个整数表示答案。
样例输入

2 1
2 2 4
4 4 2
0 0 5
1
2
3
4

样例输出

2
1

样例说明

示例图如下，排雷火箭 1 覆盖了炸雷 1，所以炸雷 1 被排除；炸雷 1 又覆盖了炸雷 2，所以炸雷 2 也被排除。

图片描述

评测用例规模与约定

对于 40 的评测用例: 0≤x,y≤109,0≤n,m≤103,1≤r≤10

对于 100 的评测用例: 0≤x,y≤109,0≤n,m≤5×104,1≤r≤10

运行限制

最大运行时间：1s
最大运行内存: 256M

题目思路

代码演示

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

struct node {
	int x, y, r;
};

int ans = 0;
int n, m;
map<pair<int, int>, int> mp;
set<pair<int, int> > s;
queue<node> q;

int get_len(int x, int y, int i, int j) {
	return (x - i) * (x - i) + (y - j) * (y - j);
}

int main() {
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		int x, y, r;
		cin >> x >> y >> r;
		int tmp = mp[{x, y}] + 100; 
		mp[{x, y}] = max(tmp, tmp / 100 * 100 + r);
	}
	for (int i = 0; i < m; i++) {
		int x, y, r;
		cin >> x >> y >> r;
		q.push(node({ x,y,r }));
	}
	int ans = 0;
	while (q.size()) {
		int xx = q.front().x;
		int yy = q.front().y;
		int rr = q.front().r;
		q.pop();
		for (int i = xx - rr; i <= xx + rr; i++) {
			for (int j = yy - rr; j <= yy + rr; j++) {
				pair<int, int> p(i, j);
				if (s.count(p)) 
					continue;
				if (!mp.count(p))
					continue;
				if (get_len(xx, yy, i, j) > rr*rr) 
					continue;
				s.insert(p);
				q.push(node({ i,j,mp[p] % 100 }));
				ans = ans + mp[p] / 100;
			}
		}
	}
	cout << ans;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

I：李白打酒加强版

问题描述

话说大诗人李白, 一生好饮。幸好他从不开车。

一天, 他提着酒显, 从家里出来, 酒显中有酒 2 斗。他边走边唱:

无事街上走，提显去打酒。 逢店加一倍, 遇花喝一斗。
1

这一路上, 他一共遇到店 N 次, 遇到花 M 次。已知最后一次遇到的是花, 他正好把酒喝光了。

请你计算李白这一路遇到店和花的顺序, 有多少种不同的可能?

注意: 显里没酒 ( 0 斗) 时遇店是合法的, 加倍后还是没酒; 但是没酒时遇 花是不合法的。
输入格式

第一行包含两个整数 N 和 M.
输出格式

输出一个整数表示答案。由于答案可能很大，输出模 1000000007 的结果.
样例输入

5 10
1

样例输出

14
1

样例说明

如果我们用 0 代表遇到花，1 代表遇到店，14 种顺序如下：

010101101000000

010110010010000

011000110010000

100010110010000

011001000110000

100011000110000

100100010110000

010110100000100

011001001000100

100011001000100

100100011000100

011010000010100

100100100010100

101000001010100

评测用例规模与约定

对于 40% 的评测用例: 1≤N,M≤10 。

对于 100%100% 的评测用例: 1≤N,M≤100 。

运行限制

最大运行时间：1s
最大运行内存: 256M

题目思路

动态规划，f[i][j][k] 表示在第 i 个位置，遇到第 j 个花，目前还剩 k 斗酒。
当遇到花时：f[i][j][k] =f[i - 1][j - 1][k + 1];
当遇到酒时：f[i][j][k] = (f[i][j][k] + f[i - 1][j][k / 2]) % mod;

代码演示

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
int n, m;
int f[205][105][105];  
int main() {
    cin >> n >> m;
    f[0][0][2] = 1;
    for (int i = 1; i <= n + m; i++) {
        for (int j = 0; j <= m; j++) {
            for (int k = 0; k <= m; k++) {  
                if(j>=1) 
                	f[i][j][k] =f[i - 1][j - 1][k + 1];
                if (k % 2 == 0)   
                    f[i][j][k] = (f[i][j][k] + f[i - 1][j][k / 2]) % mod;
            }
        }
    }
    cout << f[n + m - 1][m - 1][1];
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

J：砍竹子

问题描述

这天, 小明在砍竹子, 他面前有 n 棵竹子排成一排, 一开始第 i 棵竹子的 高度为 hi​.

他觉得一棵一棵砍太慢了, 决定使用魔法来砍竹子。魔法可以对连续的一 段相同高度的竹子使用, 假设这一段竹子的高度为 H, 那么

用一次魔法可以 把这一段竹子的高度都变为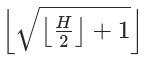

​, 其中 ⌊x⌋ 表示对 x 向下取整。小明想 知道他最少使用多少次魔法可让所有的竹子的高度都变为 1 。
输入格式

第一行为一个正整数 nn, 表示竹子的棵数。

第二行共 nn 个空格分开的正整数 hihi​, 表示每棵竹子的高度。
输出格式

一个整数表示答案。
样例输入

6
2 1 4 2 6 7
1
2

样例输出

5
1

样例说明

其中一种方案：

21426214267
→214262→214222→211222→111222→111111
共需要 5 步完成

评测用例规模与约定

对于 20% 的数据, 保证 n≤1000,hi≤106。 对于 100% 的数据, 保证 n≤2×105,hi≤1018 。

题目思路

代码演示

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
int sum = 0;
vector<int>cnt1;
vector<int>cnt2;
ll cnt(ll h) {
	return sqrtl(h / 2 + 1);
}
int main() {
	int n;
	ll h;
	cin >> n;
	while (n--) {
		cin >> h;
		while (h != 1) {
			cnt2.push_back(h);
			h = cnt(h);
		}
		int i = cnt1.size() - 1, j = cnt2.size() - 1;
		while (i >= 0 && j >= 0 && cnt1[i] == cnt2[j]) i--, j--;
		sum += j + 1;
		cnt1 = cnt2;
		cnt2.clear();
	}
	cout << sum;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29