【C语言】二分查找（含图解）_二分查找c语言

1. 二分查找思想

二分法：二分查找算法是一种在有序数组中查找某一特定元素的搜索算法，其思想就是不断地将有序查找表“一分为二”，逐渐缩小搜索区域，进而找到目标元素。

• 搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜 素过程结束；
• 如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。
• 如果在某一步骤数组 为空，则代表找不到。
• 这种搜索算法每一次比较都使搜索范围缩小一半。折半搜索每次把搜索区域减少一半，时间复杂度为Ο(logn) 。

注：使用二分查找的前提条件是，数组已经是有序的

二分查找图解：以有序数组 {10, 14, 19, 26, 27, 31, 33, 35, 42, 44} 为例，查找元素 33。

初始状态：

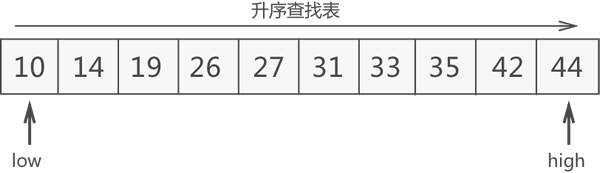
第一轮查找：根据 27<33，可以判定 33 位于 27 右侧的区域，更新搜索区域为元素 27 右侧的区域。

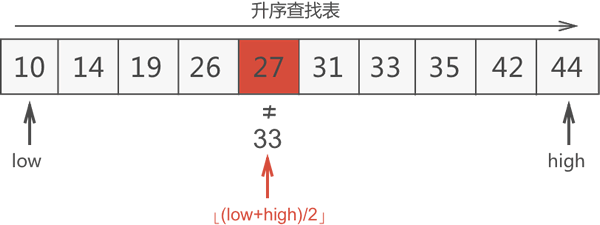
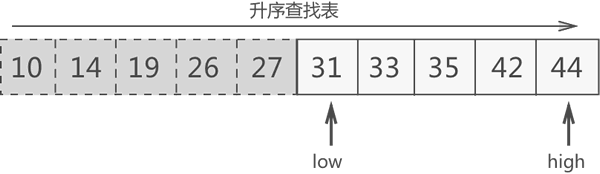
第二轮查找：35>33，可以判定 33 位于 35 左侧的区域，更新搜索区域。

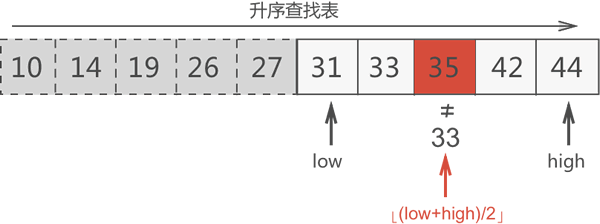
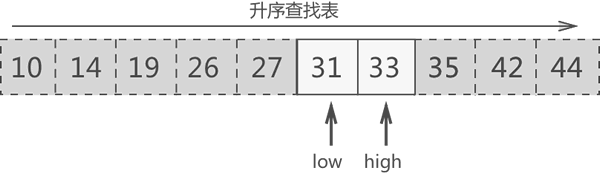
第三轮查找：31<33，可以判定 33 位于 31 右侧的区域，更新搜索区域。

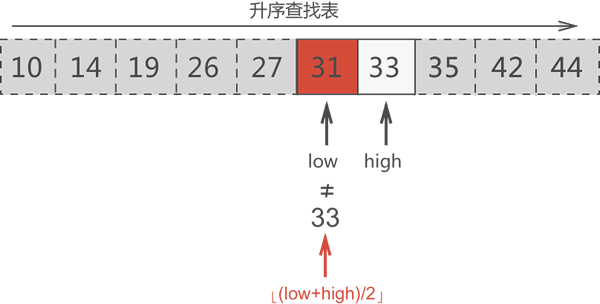
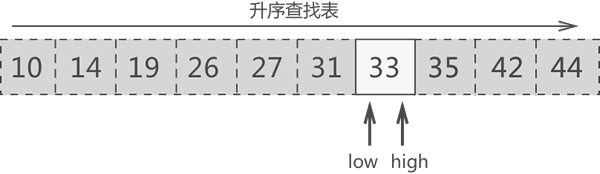
第四轮查找：搜索区域内中间元素的位置是 [(7+7)/2]=7，因此中间元素是 33，此元素就是要找的目标元素。

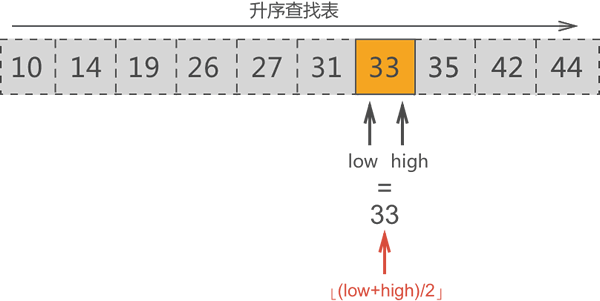
2. 代码实现

2.1 未封装函数

代码实现思路：

• 定义low、high、mid，分别代表最小值、最大值和中间值的下标，并且初始赋值low指向第一个元素，high指向最后一个元素；定义target代表要查找的目标值。
• 进行循环二分查找，循环的条件是左边界还未超过右边界(low <= high)，当左边界超过右边界，说明查找结束了。
• 对比目标值与中间值的大小，如果两者相等说明查找到了（该值的下标就是中间值的下标mid）；如果目标值大于中间值，说明目标值在左半边，此时缩小右边界的范围 (high = mid - 1)重新查找；如果目标值小于中间值，说明目标值在右半边，此时缩小左边界的范围 (low = mid + 1)重新查找。

#include <stdio.h>
#define N 11

int main() 
{
	int a[N] = {1, 5, 8, 11, 19, 22, 31, 35, 40, 49, 50}; // 准备好一个已经排序好的数组
	int low = 0, high = N - 1, mid, target; 
	printf("请输入要查找的值：");
	scanf("%d", &target);
	printf("%d\n", target);
	
	// 当左边界还未超过右边界时，进行二分查找
	while(low <= high)
	{
		mid = (low + high) / 2; // 每次循环重新给mid赋值，改变中间值的下标
		printf("low = %d, high = %d, mid = %d\n", low, high, mid); // 此处打印各个下标值，方便观测下标变化
		// 如果中间值等于目标值，说明查找成功，此时跳出循环
		if(a[mid] == target){
			printf("目标值的下标是%d\n", mid);
			break;
		}
		// 如果中间值大于目标值，说明目标值在左半边，此时改变右边界的下标（缩减右半边）
		if(a[mid] > target)
			high = mid - 1;
		// 如果中间值小于目标值，说明目标值在右半边，此时改变左边界的下标（缩减左半边）
		if(a[mid] < target)
			low = mid + 1;
	}
	
	// 当左边界已经超过右边界时，说明查找已经结束
	if(low > high)
		printf("未找到目标值\n");
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

注：以上代码适用于数组已经是升序排序的情况下。

运行结果如下：

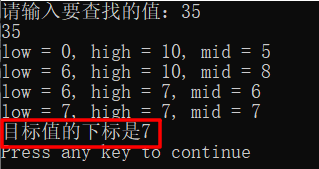
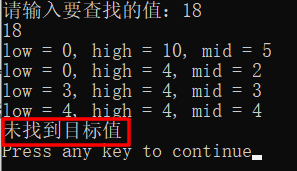
2.2 封装函数（使用while循环）

使用while循环，将二分查找封装成函数，代码如下：

#include <stdio.h>

// 二分查找，找到元素返回索引值，否则返回-1
int binarySearch(int arr[], int len, int target) {
	int low = 0, high = len -1, mid; // 最小值、最大值和中间值的下标
	while(low <= high) {
		mid = (low + high) / 2; // 每次循环重新给mid赋值，改变中间值的下标
		if(arr[mid] == target) { // 如果中间值等于目标值，说明查找成功，返回下标
			return mid;
		} else if(arr[mid] > target) { // 如果中间值大于目标值，说明目标值在左半边，此时缩减右半边
			high = mid -1;
		} else { // 如果中间值小于目标值，说明目标值在右半边，此时缩减左半边
			low = mid + 1;
		}
	}
	return -1;
}

int main() {
	int a[] = {1, 5, 8, 11, 19, 22, 31, 35, 40, 49, 50}; 
	int len = sizeof(a) / sizeof(int);
	int index, target;
	printf("请输入要查找的值：");
	scanf("%d", &target);
	index = binarySearch(a, len, target);
	printf("目标值的下标是%d\n", index);
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

运行结果如下：

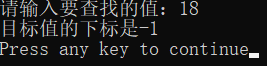
2.3 封装函数（使用递归）

使用递归调用，将二分查找封装成函数，代码如下：

#include <stdio.h>

// 二分查找，找到元素返回索引值，否则返回-1
int binarySearch(int arr[], int low, int high, int target) {
	if(low <= high) {
		int mid = (low + high) / 2; // 每次递归重新给mid赋值，改变中间值的下标
		if(arr[mid] == target) { // 如果中间值等于目标值，说明查找成功，返回下标
			return mid;
		} else if(arr[mid] > target) { // 如果中间值大于目标值，说明目标值在左半边
			high = mid -1;
			return binarySearch(arr, low , high, target); // 继续查找左半边
		} else { // 如果中间值小于目标值，说明目标值在右半边
			low = mid + 1;
			return binarySearch(arr, low , high, target); // 继续查找右半边
		}
	} else {
		return -1;
	}
}

int main() {
	int a[] = {1, 5, 8, 11, 19, 22, 31, 35, 40, 49, 50}; 
	int len = sizeof(a) / sizeof(int);
	int index, target;
	printf("请输入要查找的值：");
	scanf("%d", &target);
	index = binarySearch(a, 0, len-1, target);
	printf("目标值的下标是%d\n", index);
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

注：使用递归查找，值得注意的是，每次递归时，需要缩小查找的范围，也就是每次传入的左右边界发生了改变，因此入参必有 low 和 high，所以此处递归函数的定义是 binarySearch(int arr[], int low, int high, int target)，而不能像之前封装while循环的函数定义 binarySearch(int arr[], int len, int target)