python栈迷宫路径搜索_深度优先搜索（DFS）_栈--深度优先搜索 迷宫

.......................................................................................................................................................... 

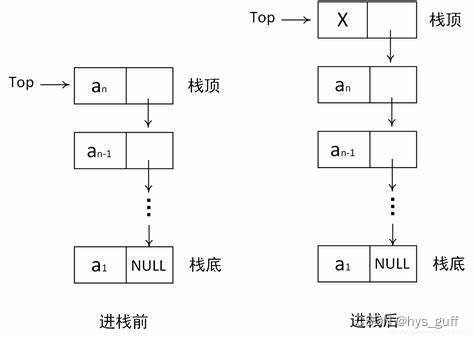
python链栈算法，DFS深度优先搜索

..........................................................................................................................................................  

.......................................................................................................................................................... 

算法通过尝试四个方向（上、下、左、右）来探索迷宫。它使用一个栈来记录当前路径。如果到达终点，它会打印路径并返回True。如果找不到路径，它会打印"走不通！"并返回False。

.......................................................................................................................................................... 

# 1. 当前所在节点四个方向分别为 x+1,y; x-1,y; x,y+1; x,y-1
# 2. 当前节点，也就是栈里的最后一个节点 stack[-1]
# 3. 当走到终点时，就可以输出栈了
# 4. 没走到终点并且下一节点能走时，把该下一节点加入栈并标记为2，表示走过了
# 5. 没走到终点，并且四个节点都不能走时，把该下一节点做个标记，并删除原来的节点（回退）
# 6. 如果一条路都不能走时，就说明没有路可以走了

.......................................................................................................................................................... 

maze = [ [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],        #1就是墙，0就是路
         [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],        #原点在左上角
         [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
         [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
         [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
         [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
         [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
         [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
         [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
         [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
# 1. 当前所在节点四个方向分别为 x+1,y; x-1,y; x,y+1; x,y-1
# 2. 当前节点，也就是栈里的最后一个节点 stack[-1]
# 3. 当走到终点时，就可以输出栈了
# 4. 没走到终点并且下一节点能走时，把该下一节点加入栈并标记为2，表示走过了
# 5. 没走到终点，并且四个节点都不能走时，把该下一节点做个标记，并删除原来的节点（回退）
# 6. 如果一条路都不能走时，就说明没有路可以走了
 
def maze_path(x1, y1, x2, y2):  # 起点终点
    dirs = [
        lambda x, y: (x + 1, y),  #lambda函数对x或y进行加减
        lambda x, y: (x, y + 1),  #g=lambda x:x+1 print(g(1))  #结果为2（匿名函数lambbda用法举例）
        lambda x, y: (x - 1, y),  #如何让二维矩阵产生直角坐标系的效果？-----maze[3][2])前y后x
        lambda x, y: (x, y - 1)
    ]  # 四个方向
    stack = [(x1, y1)]  #
    while len(stack) > 0:
        curNode = stack[-1]     #往前走的那个头的坐标
        if curNode[0] == x1 and curNode[1] == x2:
            # 判断走到终点了
            for p in stack:
                print(p)  # 打印路线
            return True #如果不在这里整一个返回值的话，最下面的“走不通”
        # 尝试四个方向 上：x-1，y 下：x+1,y 左:x,y-1 右： x,y+1
        for dir in dirs:  #for 循环让上下左右每一条路都尝试一下
            nextNode = dir(curNode[0], curNode[1]) #更新前进的头的位置
            if maze[nextNode[0]][nextNode[1]] == 0: #nextNode[0]是curNode[0],curNode[0]是当前结点的x1，curNode[1]是当前结点的y1
                stack.append(nextNode)#只有是0，1才会更新栈顶
                maze[nextNode[0]][nextNode[1]] = 2 #没走到终点并且下一节点能走时，把该下一节点加入栈并标记为2，表示走过了
                break #跳出for循环
        else:   # 如果当前的路线走到死胡同时，把当前节点标记成2，并且出栈
            maze[nextNode[0]][nextNode[1]] = 2 #将零变成二
            stack.pop()
    else:
        print('走不通！')
        return False
 
 
maze_path(1, 4, 8, 7)

.......................................................................................................................................................... 

深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索树或图的算法。它从起始节点开始，沿着一条路径尽可能深入地探索，直到无法继续前进，然后回溯到上一个节点，继续探索其他路径，直到遍历完所有节点。

DFS的基本思想是使用栈来保存待探索的节点。算法的步骤如下：

1. 将起始节点放入栈中。
2. 从栈中弹出一个节点作为当前节点。
3. 检查当前节点是否为目标节点。如果是，则算法结束。
4. 如果当前节点不是目标节点，则将当前节点标记为已访问，并将其未访问的邻居节点（如果有）放入栈中。
5. 重复步骤2-4，直到栈为空或找到目标节点。

DFS的特点是深度优先，即尽可能深入地搜索。它不保证找到最短路径，但可以找到一条路径。在搜索问题中，DFS常用于解决迷宫问题、图的连通性问题、拓扑排序等。

然而，DFS也具有一些缺点。由于其深度优先的特性，它可能陷入无限循环，特别是在存在环的图中。此外，DFS不一定能找到最优解，因为它只关注一条路径，而不是搜索所有可能的路径。

为了应对DFS的缺点，可以使用一些技巧，如设置最大搜索深度、使用剪枝策略、记录已访问节点等。

.......................................................................................................................................................... 

Guff_hys_python数据结构,大数据开发学习,python实训项目-CSDN博客

 ..........................................................................................................................................................