- 1已解决EROR 1064 (42000): You have an error in. your SOL syntax. check the manual that corresponds to yo_you have an error in your sol syntax; check the ma
- 2Hadoop学习日记-HDFS分布式文件存储系统整体概述_namenode和datanode分布式存储
- 3阿里云Big Data - |分层| ODS& DWD& DWS& ADS| 行为数仓_dws表 data
- 4一文读懂非关系型数据库(NoSQL)
- 5百度安全多篇议题入选Blackhat Asia以硬技术发现“芯”问题
- 6Locust性能测试教程_locust 性能测试
- 7Linux 常用命令与教程_/sbin:/usr/sbin:/usr/local/sbin:/root/bin:/usr/loc
- 8论文阅读:(AAAI 2019)M2det: A single-shot object detector based on multi-level feature pyramid network_a detector based on dl
- 9LCD1602命令代码整合
- 10基于JAVA高考志愿辅助填报系统
【数据结构】图(Graph)
赞
踩
| 线性表 | 树 | 图 | |
|---|---|---|---|
| 数据元素 | 元素 | 结点 | 顶点 |
| 空 | 空表 | 空树 | 至少有一个顶点(有穷非空) |
| 元素关系 | 线性 | 层次 | 边 |
概念
图:由顶点的 有穷非空 集合和顶点之间的连线(边)的集合组成。通常表示为 G=(V, E),其中 G 表示一个图,V(G)和E(G) 分别代表图 G 中的顶点集合和边集合。
注意:图不可以为空,换句话说,顶点集合 V 不可以为空集。而边集合 E 可以为空
无向图:图中任意两个顶点之间的边都是无方向的边。
对于无向图,只要两个顶点之间有一条边,则这两个顶点之间可以互相到达。
此外,无向图的边是对称的。
下图中,连接顶点 A 与 B 之间的边因为不存在方向问题,因此可以表示为无序对 (A,B) 或者 (B,A)。
注意:这里用的是
( )表示无向边。
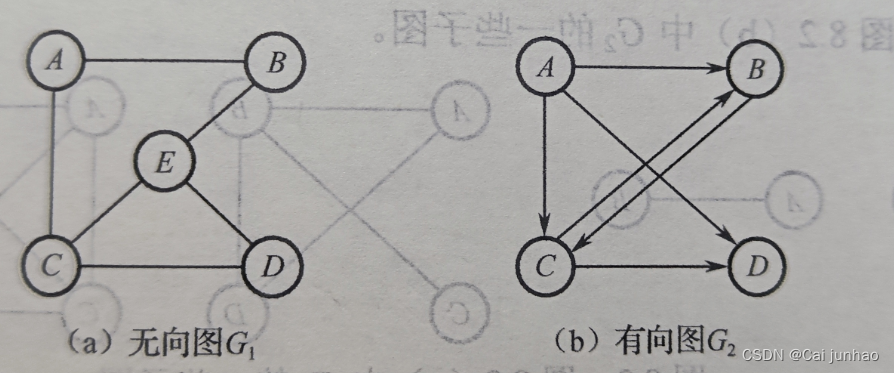
有向图:图中任意两个顶点之间的边都是有方向的边 。
在上图中,顶点 A 到 B 之间存在一条有向边(从 A 指向 B 的箭头),这表示从顶点 A 可以到达顶点 B,但因为顶点 B 到顶点 A 之间并不存在有向边,所以从顶点 B 不可以到达顶点 A。
顶点 A 到顶点 B 的有向边(箭头)就是弧。箭头开始的顶点 A 叫 弧尾,箭头指向的顶点 B 叫 弧头。这条弧可以用 <A,B> 表示,注意这里用的是 尖括号 表示有向边。另外还需要注意方向,不可以写成 <B,A>。
简单图:图中若不存在 顶点到其自身 的边,并且同一条边 不会重复 出现。
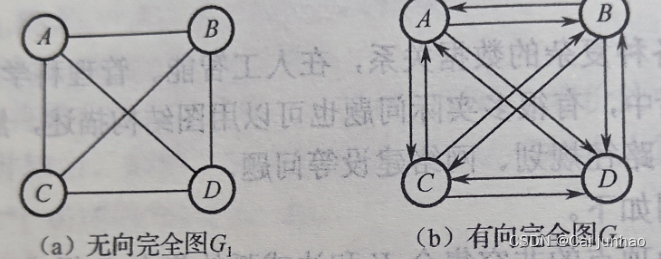
无向完全图:在无向图中,如果任意两个顶点之间都存在边 。
含有 n 个顶点的无向完全图有 n ( n − 1 ) / 2 n(n−1)/2n(n−1)/2 条边
有向完全图:在有向图中,如果任意两个顶点之间都存在方向相反的两条弧。
含有 n 个顶点的有向完全图有 n ( n − 1 ) n(n-1)n(n−1) 条边
稀疏图与稠密图:有很少条边或者弧的图为稀疏图,反之为稠密图。
回路(环):把第一个顶点和最后一个顶点相同的路径。
简单回路 / 简单环:除第一个顶点和最后一个顶点,其余顶点不重复出现的回路。
简单路径:在路径序列中顶点不重复出现的路径。
路径长度:路径上的边或弧的数目。
度:与顶点v相关联的边的数目。
出度:以v为起点的弧的数目
入度:以v为终点的弧的数目
顶点v的度是其入度和出度之和。
一个具有n个顶点,e条边或弧的图,所有顶点的度之和是边数的2倍。
连通:若从u到v存在路径,则称u到v是连通的。
连通图:V(G)中每对不同顶点u和v都连通的图。
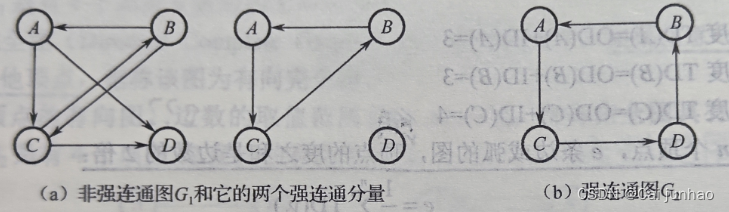
连通分量:无向图中的极大连通子图。
强连通图:有向图中,堆V(G)中每对不同的顶点u,v都存在从u到v及从v到u的路径。
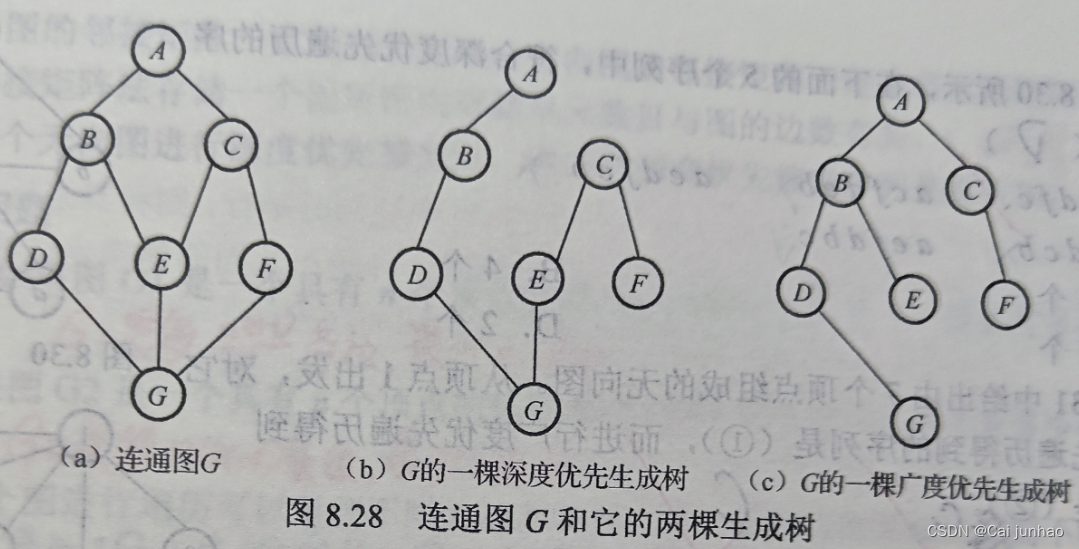
生成树:是连通图的最小连通子图,含有图中全部n个结点,但只有n-1条边。在生成树中添加一条边之后,必然会形成回路或环。
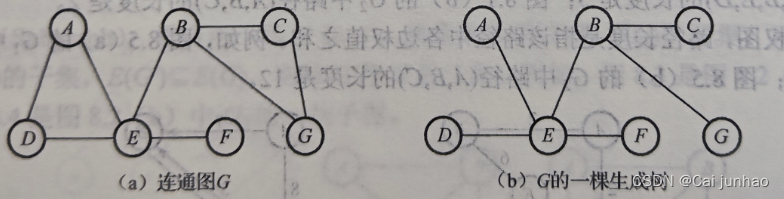
子图:有两个图G和G*,满足V(G*)是V(G)的子集,E(G*)是E(G)的子集,则称G*是G的子图。
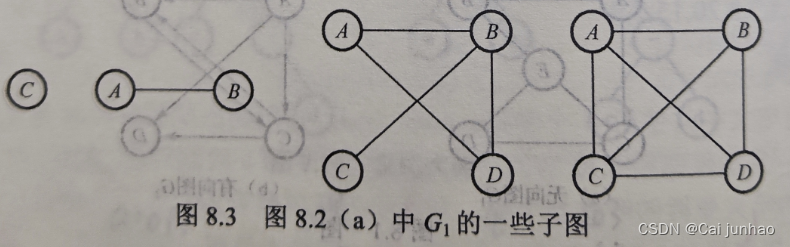
有向树:只有一个顶点的入度为0,其余顶点的入度为1的有向图。
有向树是弱连通图。
具体的概念可以看这篇:图 —— 基础概念详解
图的存储方式
除了要存储各个顶点本身的数据信息外,还要存储边的信息。
邻接矩阵
邻接矩阵表示法
存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵A是一个n ∗ n的方阵,定义为:
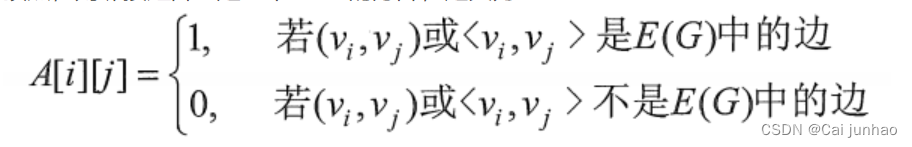
(1)无向图的邻接矩阵
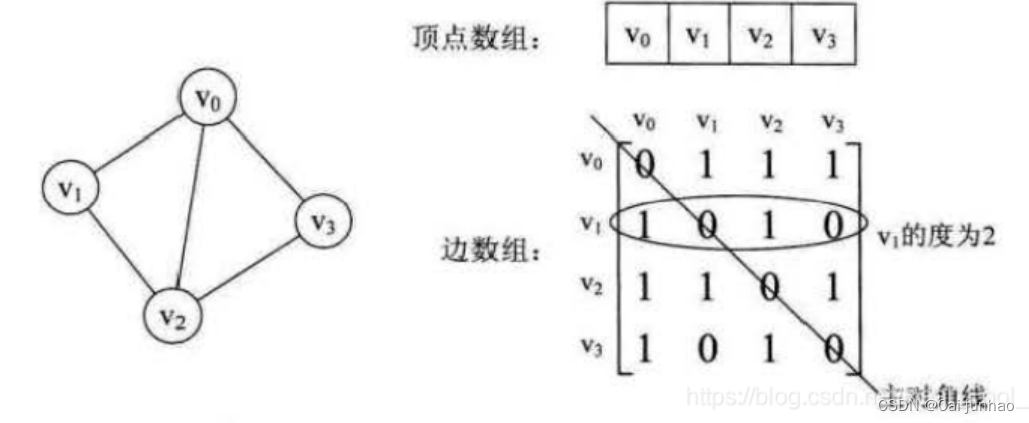
特点:
• 无向图的邻接矩阵一定是一个对称矩阵。 因此,在实际存储邻接矩阵时只需存储上(或下)三角矩阵的元素。
• 第 i 行(或第 i 列)非零元素的个数,是第 i 个顶点的度
(2)有向图的邻接矩阵
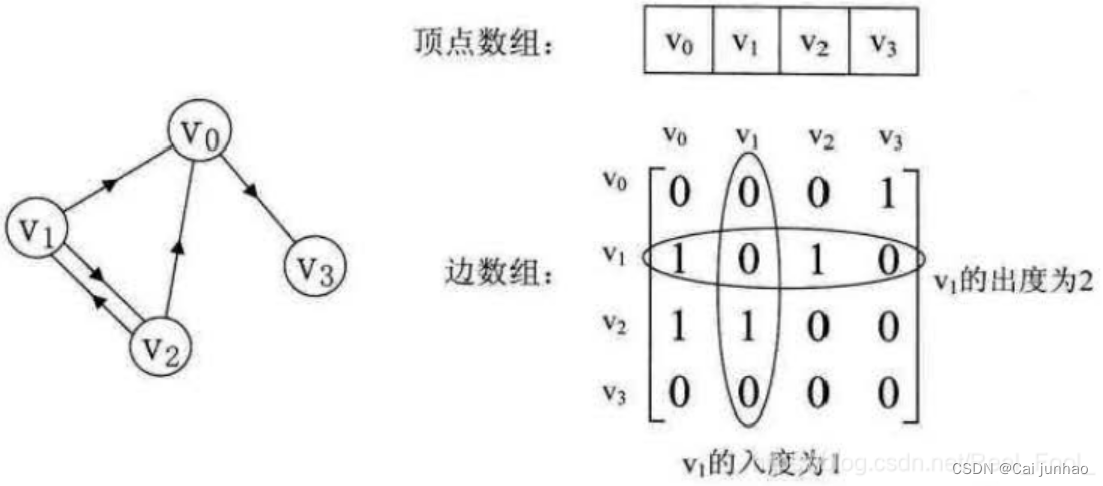
特点:
• 主对角线上数值依然为0,但矩阵并不一定对称。
• 第 i 行非零元素的个数,是第 i 个顶点的出度
• 第 i 列非零元素的个数,是第 i 个顶点的入度
(3)网的邻接矩阵
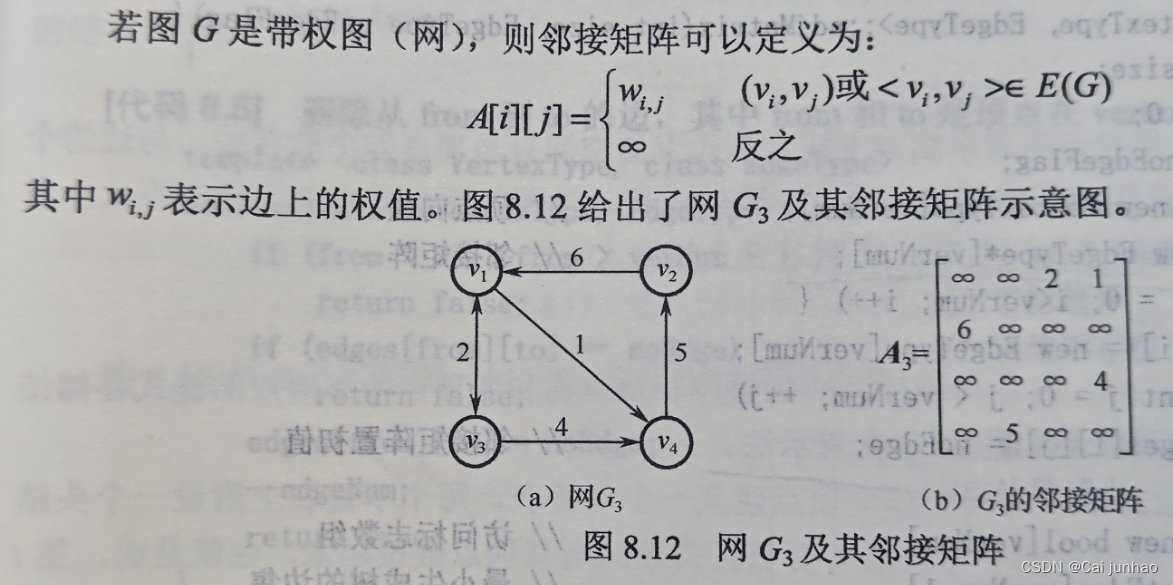
邻接矩阵表示法的特点
(1)图的邻接矩阵表示是唯一的。
(2)含有n个顶点的图,其邻接矩阵的空间代价是O(n2),与图的顶点数相关,与边数无关。
邻接表
邻接表表示法
邻接表:将图的顶点的顺序存储结构和各顶点的邻接点的链式存储结构相结合的存储方式,类似于数的孩子链表法。
边表:为图中每个顶点建立一个单链表,每个单链表上附设有一个头结点。
图的边表结点:邻接点域 to 表示与顶点 i 相邻接的顶点在顶点向量中的序号
顶点表:每个链表设立一个头结点,头结点有2个域。数据域vertex存储结点 i 的数据信息,指针域firstEdge指向 i 的第一个邻接点。

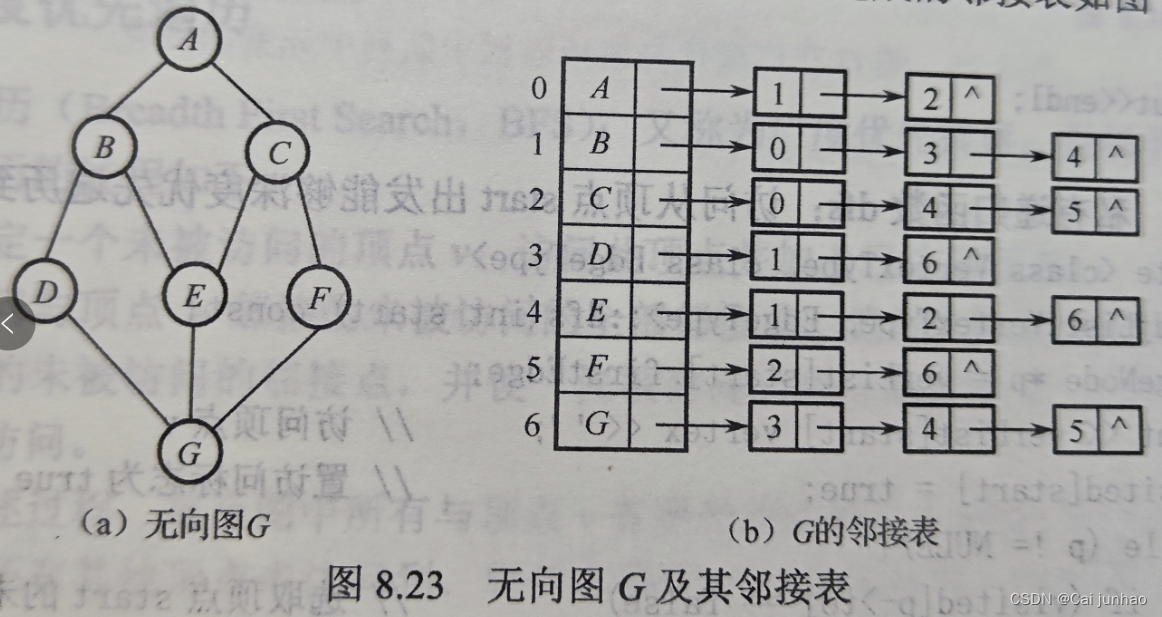
无向图及其邻接表示意图如下。第i个边表中结点的个数等于顶点vi的度。
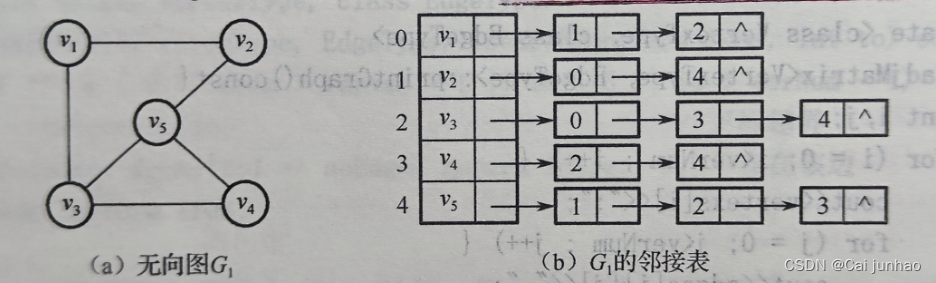
有向图及其邻接表示意图如下。第i个边表中结点的个数等于顶点vi的出度,若要求顶点vi的入度,则需遍历整个邻接表。
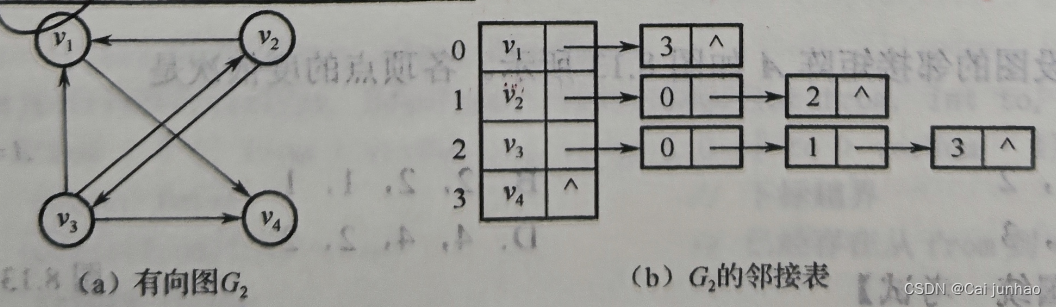
邻接表表示法的特点
(1)图的邻接表表示不唯一.
(2)邻接表的空间代价是O(n+e),内存=结点数+边数。
(3)在边稀疏的情况下,用邻接表表示比用邻接矩阵更节约空间。
(4)在邻接表上容易找到任意顶点的第一个邻接点和下一个邻接点,但要判定任意两个顶点vi,vj之间是否有边或弧相连,这需要遍历第i个或第j个链表,在这方面不如邻接矩阵方便。
(5)邻接表是图的标准存储方式。
邻接表表示法的定义与实现
一个图的邻接表存储结构可描述如下,edgeNode为边表结点类型,verNode为顶点结点类型:
#ifndef _ADJ_LIST_GRAGH_H_ #define _ADJ_LIST_GRAGH_H_ #include "graph.h" template <class VertexType, class EdgeType> class adjList :public graph<VertexType,EdgeType> { private: struct edgeNode { // 边表结点类型 int to; // 边的终点编号(在顶边表中的下标) EdgeType weight; // 边上的权值 edgeNode *next; // 指向下一个边表结点 edgeNode(){ } // 无参构造函数 edgeNode(int t, EdgeType w, edgeNode *n = NULL){ to = t; weight = w; next = n; } }; struct verNode{ // 顶点结点类型 VertexType vertex; // 顶点信息 edgeNode *firstEdge; // 指向第一个邻接点的指针 verNode(edgeNode *h = NULL) { firstEdge = h; } }; verNode *verList; // 顶点表 int *topOrder; //保存拓扑排序,用于求关键路径 void dfs(int start) const; // 从start号顶点出发深度优先遍历图 public: adjList(int size); ~adjList(); void createGraph(const VertexType V[],const EdgeType E[]); void printGraph()const; // 输出图 bool searchEdge(int from, int to) const; // 查找边 bool insertEdge(int from, int to, EdgeType w); // 插入一条边 bool removeEdge(int from, int to); // 删除一条边 void dfsTraverse() const; // 调用私有dfs深度优先遍历图 void bfsTraverse() const; // 广度优先遍历图 };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
查找
查找图中是否存在from到to的边,其中from和to是顶点在verList数组中的下标。
template <class VertexType, class EdgeType>
bool adjList<VertexType, EdgeType>::searchEdge(int from, int to) const{
if (from < 0 || from > this->verNum - 1 || to < 0 || to > this->verNum-1)
return false; //下标越界
edgeNode *p = verList[from].firstEdge;
while (p != NULL && p->to != to) {
p = p->next;
}
if (p ==NULL) return false; //该边不存在
else return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
插入
在图中插入从from到to的边,其中from和to是顶点在verList数组中的下标。
由于每个顶点的单链表中均无头结点,故插入边表结点时要对首元结点单独处理。
插入边可分为三种情况:
(1)当该边已经存在且权值为w时,返回false
(2)当该边不存在时,置该边的权值为w,边数计数器增大,返回true.
(3)当该边已经存在且权值不等于w时,更新边的权值为w,返回true.
template <class VertexType, class EdgeType> bool adjList<VertexType, EdgeType>::insertEdge(int from, int to, EdgeType w){ if (from < 0 || from >this->verNum - 1 || to < 0 || to > this->verNum - 1) return false; edgeNode *p = verList[from].firstEdge; edgeNode *pre; edgeNode *s; while (p != NULL && p->to < to) { //查找插入位置,单链表按to的值有序 pre = p; p = p->next; } if (p != NULL && p->to == to) { //该边已经存在 if (p->weight != w) p->weight = w; //修改权值 else return false; } else { s = new edgeNode(to,w,p); if (p == verList[from].firstEdge) //插入为首元结点 verList[from].firstEdge = s; else pre->next = s; //在链表其他位置上插入结点 this->edgeNum++; //新增一条边,边数+1 } return true; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
删除
删除从from到to的边,其中from和to是顶点在vertexs数组中的下标。由于每个顶点的单链表中均无头结点,故删除边表结点时要对首元结点单独处理。
template <class VertexType, class EdgeType> bool adjList<VertexType, EdgeType>::removeEdge(int from, int to){ if (from < 0 || from > this->verNum - 1 || to < 0 || to > this->verNum - 1) return false; //下标越界 edgeNode *p = verList[from].firstEdge; edgeNode *pre = NULL; while (p != NULL && p->to < to) { //查找边 pre = p; p = p->next; } if ( (p ==NULL) || (p->to > to)) //该边不存在 return false; if (p->to == to) { //该边存在 if (p == verList[from].firstEdge) { //该边是边表中的首元结点 verList[from].firstEdge = p->next; } else { pre->next = p->next; } delete p; this->edgeNum--; return true; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
其它
构造函数
template <class VertexType, class EdgeType>
adjList<VertexType, EdgeType>::adjList(int size){
this->verNum = size;
this->edgeNum = 0;
verList = new verNode[size];
this->visited = new bool[this->verNum];
TE = new mstEdge[this->verNum - 1];
topOrder = new int[this->verNum];
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
析构函数
template <class VertexType, class EdgeType> adjList<VertexType, EdgeType>::~adjList(){ int i; edgeNode *p; for (i = 0;i < this->verNum;i++) { //释放边表 while ( (p = verList[i].firstEdge) != NULL) { //释放第i个单链表 verList[i].firstEdge = p->next; delete p; } } delete[] verList; //释放顶点表 delete[] this->visited; delete[] TE; delete[] topOrder; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
创建图
其中V为顶点数组,E为经过降维的邻接矩阵。
template <class VertexType, class EdgeType>
void adjList<VertexType, EdgeType>::createGraph(const VertexType V[],const EdgeType E[]){
int i, j;
for (i = 0;i < this->verNum;i++) {
verList[i].vertex = V[i];
}
for (i = 0;i < this->verNum;i++) {
for (j = 0;j < this->verNum;j++) {
if (E[i * this->verNum + j] > 0) {
insertEdge(i,j,E[i * this->verNum + j]); //插入边按to值有序
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
输出图
template <class VertexType, class EdgeType>
void adjList<VertexType, EdgeType>::printGraph()const{
int i;
for (i = 0; i<this->verNum ; i++) {
cout<<verList[i].vertex<<":";
edgeNode *p = verList[i].firstEdge;
while (p != NULL){ // 查找顶点v未被访问的临接点
cout << verList[p->to].vertex <<","<<p->weight<< ' '; // 访问顶点p->to
p = p->next;
}
cout<<endl;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
图的遍历
对于给定图G=(V,E),从顶点v出发,按照某种次序访问G中的所有顶点,使每个顶点倍访问一次且仅被访问一次。
有两种遍历图的方法:圣都优先遍历和广度优先遍历。它们对有向图和无向图都适用。
深度优先遍历(DFS)
又称深度优先搜索,类似于树的前序遍历,尽可能先对纵深方向进行搜索。
遍历过程:
(1)选定一个未被访问的顶点v,访问此顶点并加上已访问标志。
(2)依次选顶点v的未被访问的邻接点出发,深度优先遍历图
(3)重复上述过程,直到所有和顶点v有路径相通的顶点都被访问到。
(4)如果还有顶点未被访问,则从步骤一开始。
深度优先遍历图的公共接口函数:
template <class VertexType, class EdgeType> void adjList<VertexType, EdgeType>::dfsTraverse() const{ int i; int count = 0; for (i = 0;i < this->verNum;i++) { this->visited[i] = false; } for (i = 0;i < this->verNum;i++) { if (!this->visited[i]) { dfs(i); count++; } } cout<<endl; cout<<"无向图连通分量个数:"<<count<<endl; // 无向图中,count为连通分量个数 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
基于邻接表的私有递归函数dfs
访问从顶点start出发能够深度优先遍历到的所有顶点。
基于邻接表的深度优先遍历算法,时间复杂度O(n+e)
基于邻接矩阵的深度优先遍历算法,时间复杂度O(n2)
template <class VertexType, class EdgeType>
void adjList<VertexType, EdgeType>::dfs(int start) const{
edgeNode *p = verList[start].firstEdge;
cout << verList[start].vertex << ' ';
this->visited[start] = true;
while (p != NULL) {
if (this->visited[p->to] == false) {
dfs(p->to);
}
p = p->next;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
广度优先遍历(BFS)
又称广度优先搜索,类似于树的层次遍历。
遍历过程如下:
(1)选定一个未被访问的顶点v,访问此顶点并加上已访问标志。
(2)依次访问与顶点v的未被访问的全部邻接点,然后从这些访问过的琳邻接点出发依次访问它们各自的未被访问的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。
(3)重复上述过程,直到所有和顶点v有路径相通的顶点都被访问到。
(4)如果还有顶点未被访问,则从步骤一开始。
对于步骤二,确定访问的顺序的过程如下:
(1)初始化一个队列。
(2)遍历从某个未被访问过的顶点开始,访问这个顶点并加上已访问标志,然后将该结点入队。
(3)在队列不空的情况下,反复进行如下操作:队头元素出队,访问该元素的所有未被访问的邻接点并加上已访问标识,再将这些邻接点依次入队。一直到队列为空。
(4)若图中还有未被访问的顶点,说明图不是连通图,则再选择任意一个未被访问过的顶点。
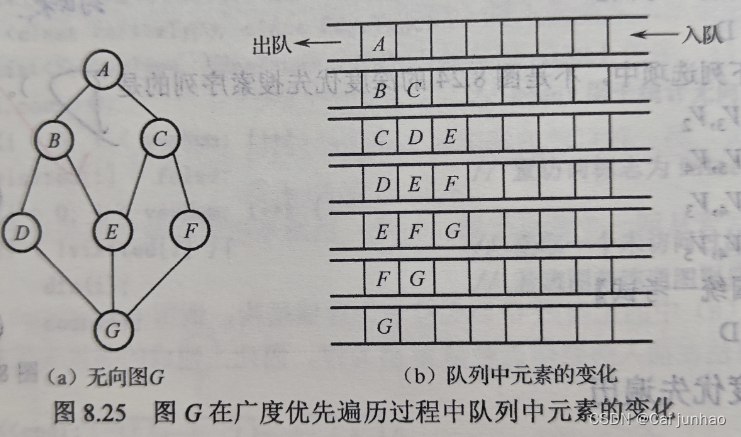
基于邻接表的广度优先遍历:
template <class VertexType, class EdgeType> void adjList<VertexType, EdgeType>::bfsTraverse()const{ int v, i; int count = 0; // 置访问标志为false queue<int> q; edgeNode *p; for (i = 0;i < this->verNum;i++) { this->visited[i] = false; } for (i = 0;i < this->verNum;i++) { if (this->visited[i] == true) continue; cout << verList[i].vertex << ' '; //访问顶点i this->visited[i] = true; //置访问标志位true q.push(i); //顶点i入队 count++; while (!q.empty()) { v = q.front(); //顶点v出队 q.pop(); p = verList[v].firstEdge; //查找顶点v未被访问的邻接点 while (p != NULL) { if (this->visited[p->to] == false) { //访问顶点v未被访问的邻接点 cout << verList[p->to].vertex << ' '; //访问顶点p->to this->visited[p->to] = true; //置访问标志位true q.push(p->to); //顶点p->to入队 } p = p->next; } } } cout<< endl; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
基于邻接表的广度优先遍历算法,时间复杂度O(n+e)
基于邻接矩阵的广度优先遍历算法,时间复杂度O(n2)
图的连接分量和生成树
生成树
一个连通图的生成树是一个极小连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。
在生成树中添加一条边之后,必定会形成回路或环。
一个连通图的生成树并不是唯一的,除非原图本身就是一颗树。
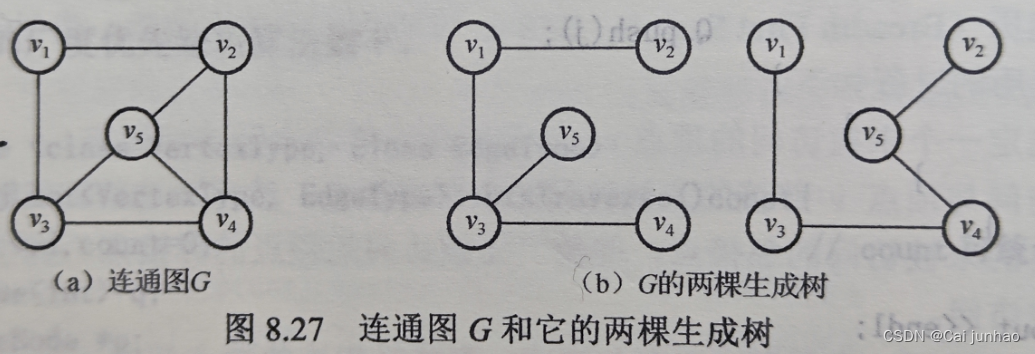
无向图G是连通图,对其进行遍历操作,如果将每次途中路过的结点和边记录下来,就得到一个子图,该子图为以源点为根生成树。
DFS和BFS都可用来测试无向图的连通性。
生成森林
若无向图G是非连通图,对其进行遍历操作,如果将每次途中路过的结点和边记录下来,就得到多颗树,从而构成森林。

习题(含408)
1.【408】若无向图G=(V,E)中含7个顶点,要保证图G在任何情况下都是连通的,求需要的边数。
当其中6个顶点构成无向完全图时,再增加一条边与第7个顶点相连,则这个含有7个顶点的无向图G在任何情况下都是连通的。
6 x (6-1) / 2 +1=16
2.【408】下列关于无向连通图特性,正确是()
A.所有顶点的度之和为偶数
B.边数大于顶点个数减1
C.至少有一个顶点的度为1
无向连通图的边数大于等于顶点个数减1.选A
3.【408】在有向图的邻接表存储结构中,顶点v在链表中出现的次数是()
A.顶点v的度
B.顶点v的出度
C.顶点v的入度
D.依附于顶点v的边数
选C
4.图的BFS生成树的树高比DFS生成树的树高 小或相等 (√)
5.一个有n个结点的连通无向图,其边的个数至少为();要连通具有n个结点的有向图,至少有()条边。
A.n-1
B.n
C.n+1
D.nlogn
选A;B
6.一个有n个结点的图,最少有()个连通分量,最多有()个连通分量。
A.0
B.1
C.n-1
D.n
选B;D
7.G是一个非连通无向图,共有28条边,求该图至少的顶点数。
在含有n个顶点的无向连通图中,边数e<=[n(n-1)]/2
当e=28时,n=8,又因为时非连通,n=9
8.n个结点的无向图,若不允许结点到自身的边,也不允许结点到结点的多重边,且边的总数为n(n-1)/2,则该无向图一定是连通图。 (√)
9.最小连通图就是最小生成树,有n-1条边。 (√)
10.若图G1是一个n个顶点的连通无向图,则图G1最多有[n(n-1)]/2条边,最少有n-1条边。
若图G2是一个n个顶点的强连通有向图,则图G1最多有n(n-1)条边,最少有n条边。
(√)