python+numpy实现DNN神经网络框架(底层原理)_python ndn

前言:

有什么写的不对的地方请大家在评论区指出来,我会及时改正,或是有什么疑问,我也会及时解答

 

1.开始架构之前我先简单介绍一下神经网络

          网络结构是输入层->隐藏层->隐藏层->···->隐藏层->输出层，在每一层中，我会首先计算Z = np.dot(W,A) + b，这叫做【linear_forward】，然后再计算relu(Z) 或者 sigmoid(Z)，这叫做【linear_activation_forward】，合并起来就是这一层的计算方法，所以每一层的计算都有这两个步骤，计算误差,然后就开始反向传播(计算出每一层w的导数),最后更新每一层参数信息

你也可以参照下图：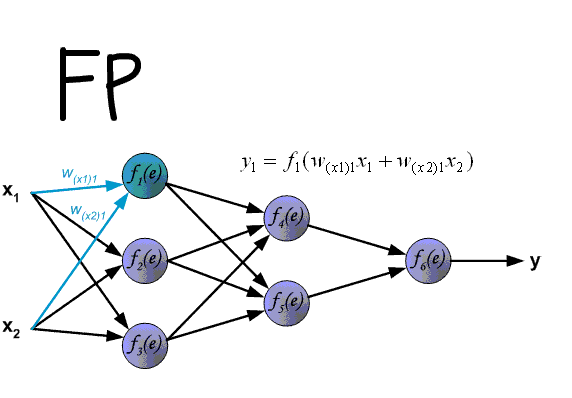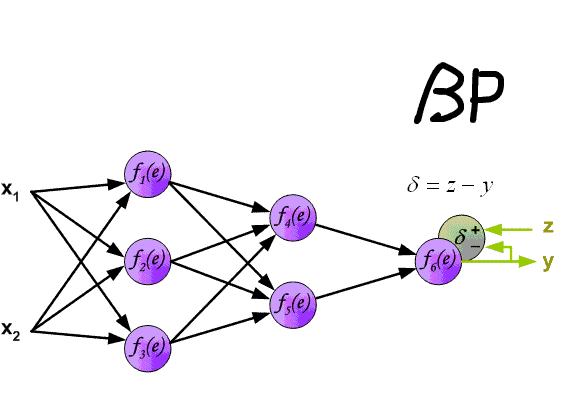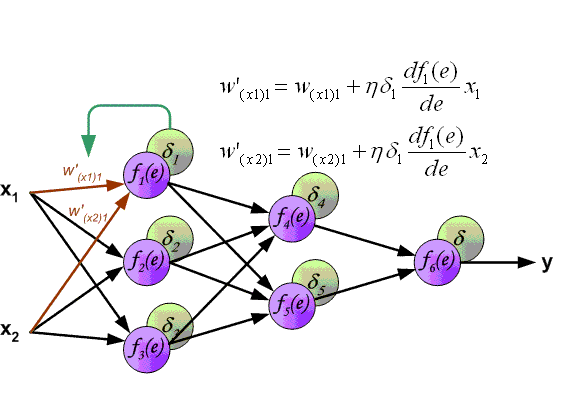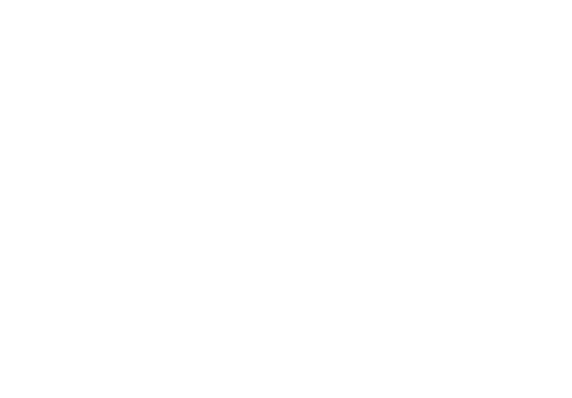 

2.下面开始手写底层代码

2.1 初始化每一层的W,b

       根据上的步骤我们先要把网络架构出来隐藏层层数,宽度,向前传输的公式是Z = np.dot(W,A) + b,我们根据这个公式定义矩阵和W,b,由公式np.dot(W,A)  得到W的形状就必须为(n,X.shape[0])n为该层的宽度,得到的节点结果就是(n,X.shape[1]),矩阵相加第一个维度要必须一样,所以b的形状就为(n,1),得到结果Z,Z经过激活函数变化后不会改变形状依然是(n,Xshape[1]),下一层隐藏层W形状就为(m,n)m为该层的宽度,b的形状为(m,1),依次类推,最后一层要和y的形状一样所以最后一个隐藏层的形状要为(Y.shape[0],上一层宽度),b的形状(Yshape[0],1),知道这样的规律后我们就可以写神经网络了

矩阵乘积如下图

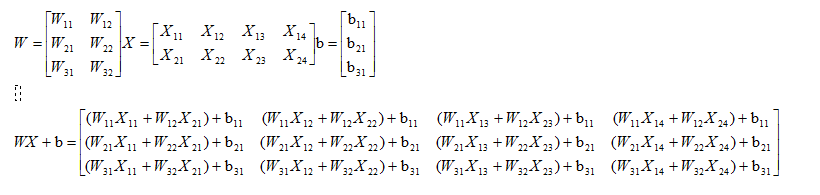
首先,我们创建一个列表来定义深度和宽度,列表的长度就是深度,列表里面的每一个值就是我们要定义的宽度

layers_dims = [X.shape[0],3,4,5,Y.shape[0]]

这个列表的意思就是 有3个隐藏层,3,4,5分别代表每一个隐藏层的宽度,下面就开始初始化我们每一层的W和b值

def initialize_parameters_deep(layers_dims):
    """
    此函数是为了初始化多层网络参数而使用的函数。
    参数：
        layers_dims - 包含我们网络中每个图层的节点数量的列表
    返回：
        parameters - 包含参数“W1”，“b1”，...，“WL”，“bL”的字典：
                     Wi - 权重矩阵，维度为（layers_dims [i]，layers_dims [i-1]）
                     bi - 偏向量，维度为（layers_dims [i]，1）
    """
    import numpy as np
    parameters={}
    L=len(layers_dims)
    for i in range(1,L):
        parameters["W"+str(i)]=np.random.normal(size=(layers_dims[i],layers_dims[i-1]))
        parameters["b"+str(i)]=np.zeros((layers_dims[i],1))
    
    return parameters

测试一下打印一下W,b的形状看一下对不对

X = np.array([[1,2,3,4],[5,6,7,8]])
Y = np.array([[0,1]])
layers_dims = [X.shape[0],3,4,5,Y.shape[0]]
parameters = initialize_parameters_deep(layers_dims)
L = len(layers_dims)
for i in range(1,L):
    print("W",i,"shape:",parameters["W"+str(i)].shape)
    print("b",i,"shape:",parameters["b"+str(i)].shape)
 
打印结果为:
W1 shape: (3, 2)
b1 shape: (3, 1)
W2 shape: (4, 3)
b2 shape: (4, 1)
W3 shape: (5, 4)
b3 shape: (5, 1)
W4 shape: (1, 5)
b4 shape: (1, 1)

layers_dims大家可以自己改变数值,和长度

2.2 向前传播

      向前传播我们从公式下手比较容易  每一层的的计算公式是一样的  Z= np.dot(W,A_prev) + b  A是前一层的值,W,b是对应当前层的值,A=激活函数(Z) 计算出来的A就是当前层的值,根据公式写代码

激活函数公式入下图

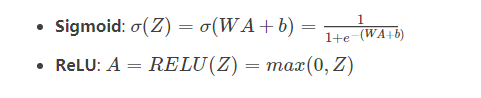
def sigmoid(Z):
    return 1/(1+np.exp(-Z))
 
 
def linear_activation_forward(A_prev,W,b,activation):
    """
    实现LINEAR-> ACTIVATION 这一层的前向传播
    参数：
        A_prev - 来自上一层（或输入层）的激活，维度为(上一层的节点数量，示例数）
        W - 权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小）
        b - 偏向量，numpy阵列，维度为（当前层的节点数量，1）
        activation - 选择在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
    返回：
        A - 激活函数的输出，也称为激活后的值
    """
    Z = np.dot(W,A_prev)+b
    if activation == "relu": 
        A = np.where(Z>0,Z,0)
    elif activation == "sigmoid":
        A = sigmoid(Z)
    
    return A

公式定义完了,就可以计算每一层的值一步一步的向前传播了,因为后面要向后传播求导,所以这里求出来的每一层的A我们都要记录一下

def L_model_forward(X,parameters):
    """
    实现[LINEAR-> RELU] *（L-1） - > LINEAR-> SIGMOID计算前向传播，也就是多层网络的前向传播，为后面每一层都执行LINEAR和ACTIVATION
    参数：
        X - 数据，numpy数组，维度为（输入节点数量，示例数）
        parameters - initialize_parameters_deep（）的输出
    返回：
        AL - 最后的激活值
        caches - 包含参数“A1”，“A2”，...，“AL”，”的字典
    """
    A = X
    cache={}
    L = len(parameters) // 2
    for i in range(1,L):
        A = linear_activation_forward(A,parameters["W"+str(i)],parameters["b"+str(i)],"relu")
        cache["A"+str(i)]=A
    A = linear_activation_forward(A,parameters["W"+str(L)],parameters["b"+str(L)],"sigmoid")
    cache["A"+str(L)]=A
    return cache

2.3计算成本

我们已经把这模型的前向传播部分完成了，我们需要计算成本（误差），以确定它到底有没有在学习，成本的计算公式如下： 

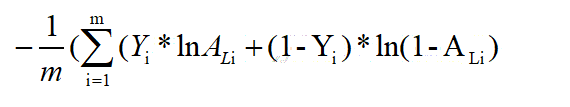
代码如下

def compute_cost(AL,Y):
    """
    成本函数。
    参数：
        AL - 与标签预测相对应的概率向量，维度为（1，示例数量）
        Y - 标签向量（例如：如果不是猫，则为0，如果是猫则为1），维度为（1，数量）
    返回：
        cost - 交叉熵成本
    """
    m = Y.shape[1]
    cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m
 
    cost = np.squeeze(cost)
 
    return cost

 

2.4反向传播

反向传播用于计算相对于参数的损失函数的梯度,下面就是求导了,我们一个一个的来求导,先是cost的导数:

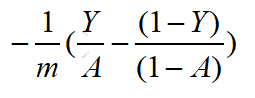
激活函数的导数 :

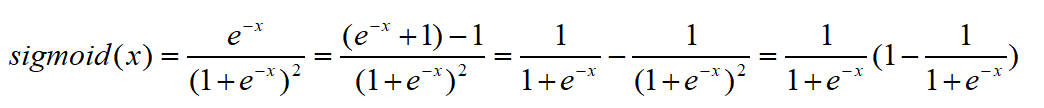
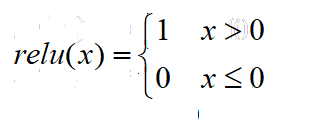
由上面的推导可得第一个倒数信息dZ:

 

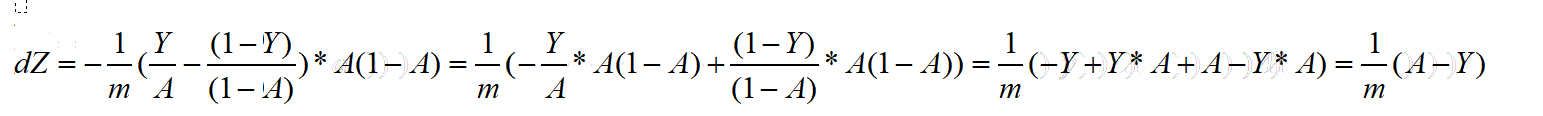
之前记录 的每个节点A值现在就要都用上了

A=WA(i-1)-b

dW=dZ*A

db=dZ

def linear_activation_backward(X,parameters,cache):
    """
    实现LINEAR-> ACTIVATION层的后向传播。
    参数：
         cache - 我们存储的用于有效计算反向传播的值的元组（值为linear_cache，activation_cache）
         activation - 要在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
    返回：
         dA_prev - 相对于激活（前一层i-1）的成本梯度值，与A_prev维度相同
         dW - 相对于W（当前层i）的成本梯度值，与W的维度相同
         db - 相对于b（当前层i）的成本梯度值，与b的维度相同
    """
    grads={}
    L=len(cache)
    dZ = cache["A"+str(L)] - Y
    for i in range(1,L):
        dW = (1 / m) * (np.dot(dZ, cache["A"+str(L-i)].T))
        db = (1 / m) * (np.sum(dZ, axis=1, keepdims=True))
        dZ =(np.dot(parameters["W"+str(L-i+1)].T,dZ))*np.where(cache["A"+str(L-i)] > 0, 1, 0)
        grads["dW"+str(L-i)]=dW
        grads["db"+str(L-i)]=db
    dW = (1 / m) * (np.dot(dZ, X.T))
    db = (1 / m) * (np.sum(dZ, axis=1, keepdims=True))
    grads["dW"+str(L-i-1)]=dW
    grads["db"+str(L-i-1)]=db
 
    return grads

2.5更新参数

我们把向前向后传播都完成了，现在我们就开始更新参数

def update_parameters(parameters, grads, learning_rate):
    """
    使用梯度下降更新参数
    参数：
     parameters - 包含你的参数的字典
     grads - 包含梯度值的字典，是L_model_backward的输出
    返回：
     parameters - 包含更新参数的字典
                   参数[“W”+ str（i）] = ...
                   参数[“b”+ str（i）] = ...
    """
    L = len(parameters) // 2 #整除
    for i in range(L):
        parameters["W" + str(i + 1)] = parameters["W" + str(i + 1)] - learning_rate * grads["dW" + str(i)]
        parameters["b" + str(i + 1)] = parameters["b" + str(i + 1)] - learning_rate * grads["db" + str(i )]
 
    return parameters

3.已经全部推完了

 

我把它封装成了一个class 

#!usr/bin/env python
#-*- coding:utf-8 _*-
 
import numpy as np
 
 
class Net(object):
 
    def __init__(self, X, Y, layers_dims, learning_rate, num_iterations, num_display, num_learn_rate=None,
                 learn_decline_rate=0.1,lambd=0.001):
 
        """
        X - 训练参数
        Y - 目标值
        layers_dims - 包含我们网络中每个图层的节点数量的列表 ,例如 [X.shape[0],3,5,Y.shape[0]]  两个隐藏层 宽度分别是3,5
        learning_rate - 学习率
        num_iterations - 迭代次数
        num_display - 每迭代多少次显示cost
        num_learn_rate - 每迭代多少次下降学习,默认None,不下降
        learn_decline_rate - 学习率下降比例 默认0.1
        
        lambd - 正则权重,默认0.001
        parameters - 包含参数“W1”，“b1”，...，“WL”，“bL”的字典：
                     Wi - 权重矩阵，维度为（layers_dims [i]，layers_dims [i-1]）
                     bi - 偏向量，维度为（layers_dims [i]，1）
        caches - 包含参数 "A1","A2",...,"AL"的字典
                Ai - 每个节点值
        grads - 包含参数“dW1”，“db1”，...，“dWL”，“dbL”的字典：
                dWi - 相对于Wi的成本梯度值，与Wi的维度相同
                dbi - 相对于bi的成本梯度值，与bi的维度相同
        L - 网络结构的深度
        """
        self.X = X
        self.Y = Y
        self.m = self.Y.shape[1]
        self.learning_rate = learning_rate
        self.layers_dims = layers_dims
        self.L = len(self.layers_dims)
        self.num_iterations = num_iterations
        self.num_display = num_display
        self.num_learn_rate = num_learn_rate
        self.learn_decline_rate = learn_decline_rate
        self.parameters = {}
        self.cache = {}
        self.grads = {}
        self.cost = 0.0
        self.lambd = lambd
        
    def softmax(self,Z):
        Z = Z - np.max(Z)
        exp_Z = np.exp(Z)
        softmax_Z = exp_Z / np.sum(exp_Z)
        return softmax_Z
    
    def sigmoid(self, Z):
        return np.float32(1 / (1 + np.exp(-Z)))
 
    def initialize_parameters_deep(self):
        """
        此函数是为了初始化多层网络参数而使用的函数。
        """
 
        for i in range(1, self.L):
            self.parameters["W" + str(i)] =np.float32 (np.random.normal(size=(self.layers_dims[i], self.layers_dims[i - 1])))
            self.parameters["b" + str(i)] =np.float32 (np.zeros((self.layers_dims[i], 1)))
 
    def linear_activation_forward(self, A_prev, W, b, activation):
        """
        实现LINEAR-> ACTIVATION 这一层的前向传播
        参数：
            A_prev - 来自上一层（或输入层）的激活，维度为(上一层的节点数量，示例数）
            W - 权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小）
            b - 偏向量，numpy阵列，维度为（当前层的节点数量，1）
            activation - 选择在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】
        返回：
            A - 激活函数的输出，也称为激活后的值
        """
        Z = np.dot(W, A_prev) + b
        assert (Z.shape == (W.shape[0], A_prev.shape[1]))
        if activation == "relu" :
            A = np.where(Z > 0, Z, 0)
        elif activation == "sigmoid" :
            A = self.sigmoid(Z)
        elif activation == "tanh" :
            A = np.tanh(Z)
        elif activation == "softmax" :
            A = self.softmax_x(Z)
        return A
 
    def L_model_forward(self):
        """
        实现[LINEAR-> RELU] *（L-1） - > LINEAR-> SIGMOID计算前向传播，也就是多层网络的前向传播，为后面每一层都执行LINEAR和ACTIVATION
        """
        A = self.X
        for i in range(1, self.L - 1):
            A = self.linear_activation_forward(A, self.parameters["W" + str(i)], self.parameters["b" + str(i)], "relu")
            self.cache["A" + str(i)] = np.float32(A)
        A = self.linear_activation_forward(A, self.parameters["W" + str(self.L - 1)],
                                           self.parameters["b" + str(self.L - 1)], "softmax")
        self.cache["A" + str(self.L - 1)] = np.float32(A)
 
    def regularization_2(self):
        L2_regularization_cost = 0.0
        for i in range(1,self.L):
            L2_regularization_cost += np.nansum(np.square(self.parameters["W"+str(i)])) 
        
        return L2_regularization_cost
        
    def pre_model_forward(self, per_X):
        """
        实现[LINEAR-> RELU] *（L-1） - > LINEAR-> SIGMOID计算前向传播，也就是多层网络的前向传播，为后面每一层都执行LINEAR和ACTIVATION
        """
        A = per_X
        for i in range(1, self.L - 1):
            A = self.linear_activation_forward(A, self.parameters["W" + str(i)], self.parameters["b" + str(i)], "relu")
            self.cache["A" + str(i)] = np.float32(A)
        A = self.linear_activation_forward(A, self.parameters["W" + str(self.L - 1)],
                                           self.parameters["b" + str(self.L - 1)], "sigmoid")
        self.cache["A" + str(self.L - 1)] = np.float32(A)
 
    def compute_cost(self):
        """
        实施定义的成本函数。
        返回：
            cost - 交叉熵成本
        """
 
        m = self.Y.shape[1]
#         self.cost = -np.sum(self.Y * np.log(self.cache["A" + str(self.L - 1)]) + (1 - self.Y) * np.log(1 - self.cache["A" + str(self.L - 1)])) / m
        self.cost = (-np.nansum(np.multiply(np.log(self.cache["A" + str(self.L - 1)]),self.Y)\
                            + np.multiply(np.log(1 - self.cache["A" + str(self.L - 1)]), 1 - self.Y)) / m)
        self.cost = np.squeeze(self.cost)
        L2_regularization_cost = self.regularization_2()
        self.cost += self.lambd * L2_regularization_cost / (2*m)
        self.cost = np.float32(self.cost)
 
    def linear_activation_backward(self):
        """
        实现LINEAR-> ACTIVATION层的后向传播。
        """
        m = self.Y.shape[1]
        dZ = self.cache["A" + str(self.L - 1)] - self.Y
        for i in range(1, self.L - 1):
            dW = (1 / self.m) * (np.dot(dZ, self.cache["A" + str(self.L - i - 1)].T)) \
            + ((self.lambd*self.parameters["W" + str(self.L - i )])/m)
            db = (1 / self.m) * (np.sum(dZ, axis=1, keepdims=True))
            dZ = (np.dot(self.parameters["W" + str(self.L - i)].T, dZ)) * np.where( \
                self.cache["A" + str(self.L - i - 1)] > 0, 1, 0)
            self.grads["dW" + str(self.L - i - 1)] = np.float32(dW)
            self.grads["db" + str(self.L - i - 1)] = np.float32(db)
        dW = (1 / self.m) * (np.dot(dZ.astype(np.float32), self.X.T)) \
        + ((self.lambd*self.parameters["W" + str(self.L - i - 1)])/m)
        db = (1 / self.m) * (np.sum(dZ.astype(np.float32), axis=1, keepdims=True))
        self.grads["dW" + str(self.L - i - 2)] = np.float32(dW)
        self.grads["db" + str(self.L - i - 2)] = np.float32(db)
 
    def update_parameters(self):
        """
        使用梯度下降更新参数
        """
        L = len(self.parameters) // 2  # 整除
        for i in range(L):
            self.parameters["W" + str(i + 1)] = self.parameters["W" + str(i + 1)].astype(np.float32) - self.learning_rate * self.grads[
                "dW" + str(i)]
            self.parameters["b" + str(i + 1)] = self.parameters["b" + str(i + 1)].astype(np.float32) - self.learning_rate * self.grads[
                "db" + str(i)]
 
    def run(self):
 
        self.initialize_parameters_deep()
 
        for j in range(self.num_iterations + 1):
            self.L_model_forward()
            self.compute_cost()
            self.linear_activation_backward()
            self.update_parameters()
 
            if self.num_learn_rate and j % self.num_learn_rate == 0 and j:
                print("当前学习率:",self.learning_rate)
                self.learning_rate -= np.multiply(self.learning_rate , self.learn_decline_rate)
                print("下降后学习率:",self.learning_rate)
                
 
            if j % self.num_display == 0:
                print("第", j, "次迭代,cost值为:" + str(self.cost))
 
    def predict(self, per_X):
        """
        返回
            predictions - 我们模型预测的向量
         """
        self.pre_model_forward(per_X)
        self.predictions = np.round(self.cache["A" + str(self.L - 1)])
 
        return self.predictions

有什么不对的地方还请多多指正