【Leetcode】547.省份数量（中等）_有 n (1 <= n <= 100)个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城

一、题目

1、题目描述

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例1：

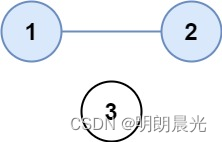
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2
1
2

示例2：

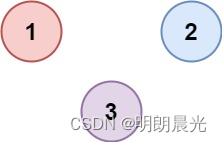
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3
1
2

2、基础框架

1

3、原题链接

547. 省份数量

二、解题报告

1、思路分析

   使用并查集将连通的岛屿放到同一个集合中，最后只需要确定集合的数量即可

2、时间复杂度

3、代码详解

C++ 版

写法一：完全利用了并查集的按秩合并和路径压缩

class Solution {
public:
    class UnionFind {
    public:
        vector<int> parents; //记录每个元素的父亲
        vector<int> size; //记录代表元素所在集合的元素个数
        vector<int> help; //辅助数组，用于路径压缩
        int sets; //集合个数

        UnionFind(int n) {
            parents.resize(n);
            size.resize(n);
            help.resize(n);
            sets = n;
            for (int i = 0; i < n; i++) {
                parents[i] = i;
                size[i] = 1;
            }
        }

        int find(int i) {
            int hi = 0;
            while (i != parents[i]) {
                help[hi++] = i;
                i = parents[i];
            }

            for (hi--; hi >= 0; hi--) { //路径压缩
                parents[help[hi]] = i;
            }

            return i;
        }

        void  myUnion(int i, int j) {
            int fi = find(i), fj = find(j);
            if (fi != fj) { //按秩合并，将集合中元素少的代表节点挂到集合中元素多的代表节点
                if (size[fi] >= size[fj]) {
                    parents[fj] = fi;
                    size[fi] += size[fj]; 
                } else {
                    parents[fi] = fj;
                    size[fj] += size[fi];
                }
                sets--;
            }
        }

        int setSize() {
            return sets;
        }

    };

    int findCircleNum(vector<vector<int>>& isConnected) {
        UnionFind *uf = new UnionFind(isConnected.size());
        for (int i = 0; i < isConnected.size(); i++) {
            for (int j = i + 1; j < isConnected.size(); j++) {
                if (isConnected[i][j] == 1) {
                    uf->myUnion(i, j);
                }
            }
        }
        return uf->setSize();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

写法二：只使用了并查集的路径压缩，并没有用到按秩合并

class Solution {
public:
    int find(vector<int> &parents, int i) {
        return parents[i] == i ? i : parents[i] = find(parents, parents[i]);
    }

    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();

        int ans = n;
        vector<int> parents(n);

        for (int i = 0; i < n; i++) {
            parents[i] = i; //初始化，每个元素都在单独的集合中
        }

        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (isConnected[i][j] == 1) {
                    int fi = find(parents, i), fj = find(parents, j);
                    if (fi != fj) { //没有按秩合并
                        parents[fi] = fj;
                        ans--;
                    }
                }
            }
        }

        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

Java 版

// 本题为leetcode原题
// 测试链接：https://leetcode.com/problems/friend-circles/
public class FriendCircles {

	public static int findCircleNum(int[][] M) {
		int N = M.length;
		// {0} {1} {2} {N-1}
		UnionFind unionFind = new UnionFind(N);
		for (int i = 0; i < N; i++) {
			for (int j = i + 1; j < N; j++) {
				if (M[i][j] == 1) { // i和j互相认识
					unionFind.union(i, j);
				}
			}
		}
		return unionFind.sets();
	}

	public static class UnionFind {
		// parent[i] = k ： i的父亲是k
		private int[] parent;
		// size[i] = k ： 如果i是代表节点，size[i]才有意义，否则无意义
		// i所在的集合大小是多少
		private int[] size;
		// 辅助结构
		private int[] help;
		// 一共有多少个集合
		private int sets;

		public UnionFind(int N) {
			parent = new int[N];
			size = new int[N];
			help = new int[N];
			sets = N;
			for (int i = 0; i < N; i++) {
				parent[i] = i;
				size[i] = 1;
			}
		}

		// 从i开始一直往上，往上到不能再往上，代表节点，返回
		// 这个过程要做路径压缩
		private int find(int i) {
			int hi = 0;
			while (i != parent[i]) {
				help[hi++] = i;
				i = parent[i];
			}
			for (hi--; hi >= 0; hi--) {
				parent[help[hi]] = i;
			}
			return i;
		}

		public void union(int i, int j) {
			int f1 = find(i);
			int f2 = find(j);
			if (f1 != f2) {
				if (size[f1] >= size[f2]) {
					size[f1] += size[f2];
					parent[f2] = f1;
				} else {
					size[f2] += size[f1];
					parent[f1] = f2;
				}
				sets--;
			}
		}

		public int sets() {
			return sets;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74