数据结构与算法1：算法效率（时间复杂度和空间复杂度）

算法效率

算法效率分为两种：第一种是时间效率，第二种是空间效率，时间效率称为时间复杂度，而空间效率被称作空间复杂度。时间复杂度主要衡量一个算法的运行速度，而空间复杂度衡量一个算法所需要的额外空间。

大O渐进表示法：

1. 用常数1取代运行时间中的所有加法常数
2. 在修改后的运行次数函数中，只保留最高阶项
3. 如果最高阶项存在且不是1，则去除与这个项目相乘的常数

时间复杂度：算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

题目1：

题目2：

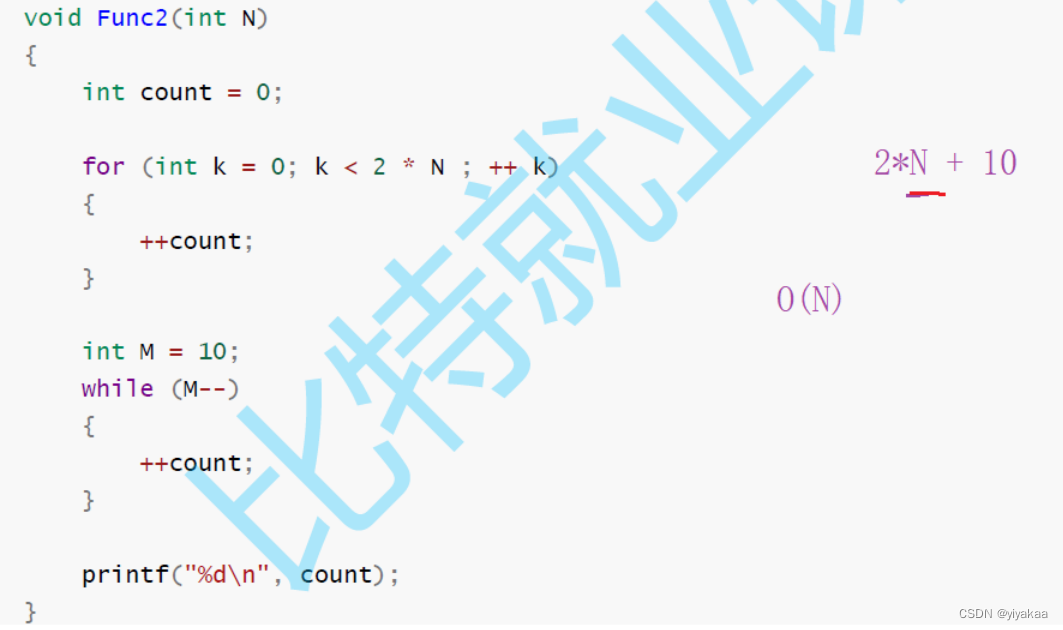
题目3：

题目4：

题目5：

另外有些算法的时间复杂度存在最好、最坏和平均情况：
最坏情况:任意输入规模的最大运行次数（上界） O(N)
平均情况：任意输入规模的期望运行次数 O(N/2)
最好情况：任意输出规模的最小运行次数（下界）O(1)
例如：在一个长度为N数组中搜索一个数据x
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到
在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

题目6：冒泡排序的时间复杂度，每一趟会逐渐减1，相当于等差数列，等差数列求和后，找影响变化最大的，所以是O(N^2)

并不是一层循环就是O(N），两次循环就是O(N^2)，具体要看程序

问题7：

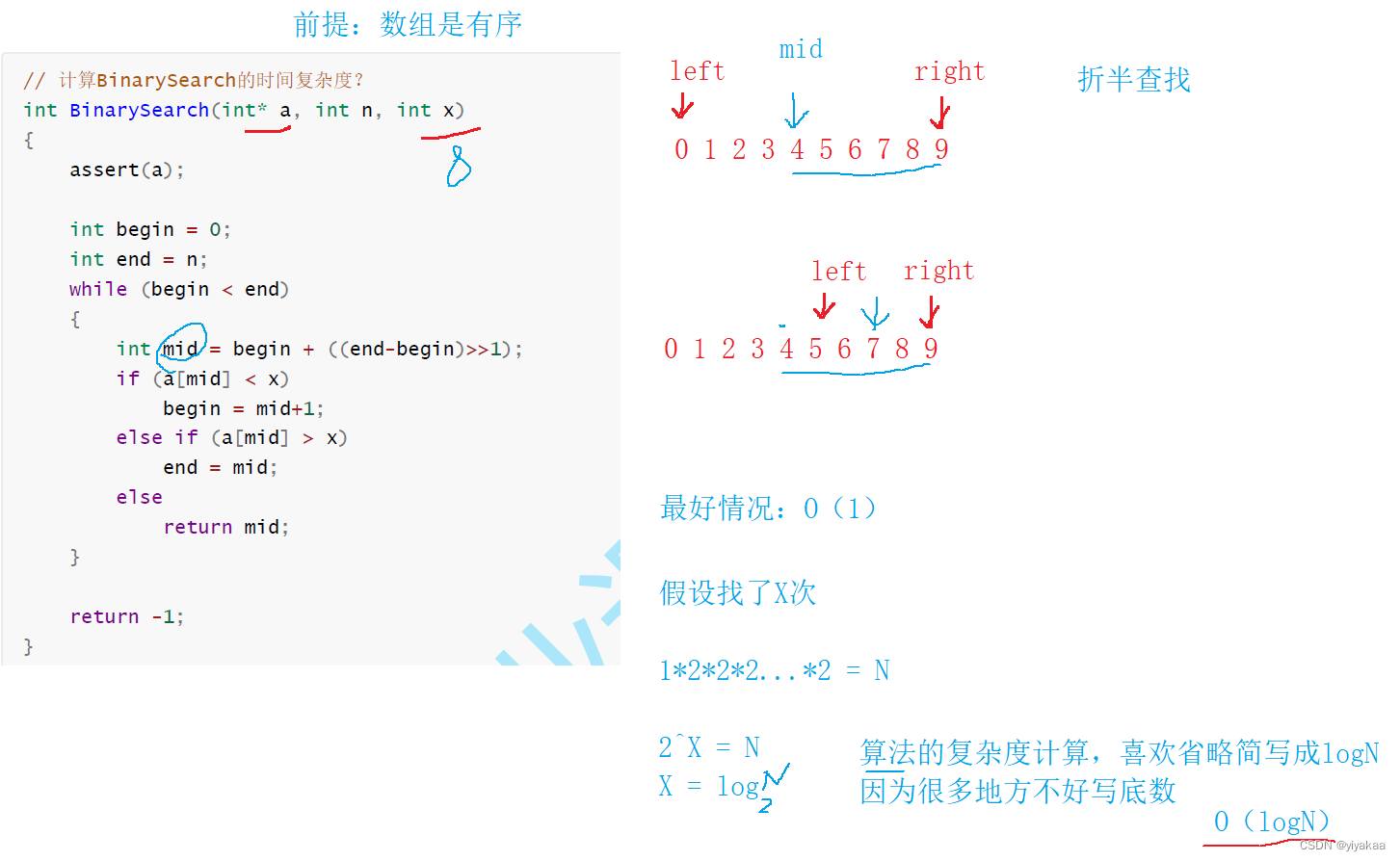
问题8：

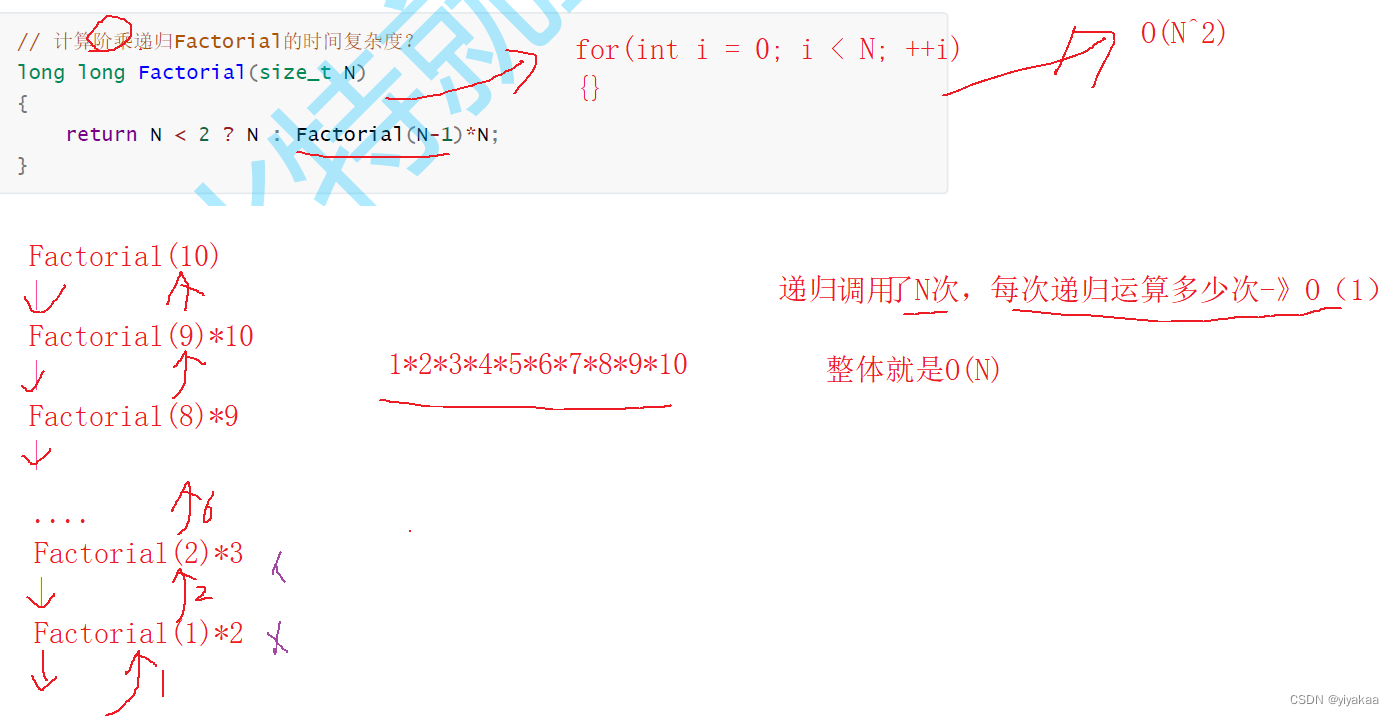
问题9：使用二分查找，在一个中国14亿排序后人中找一个人，31次也能找到

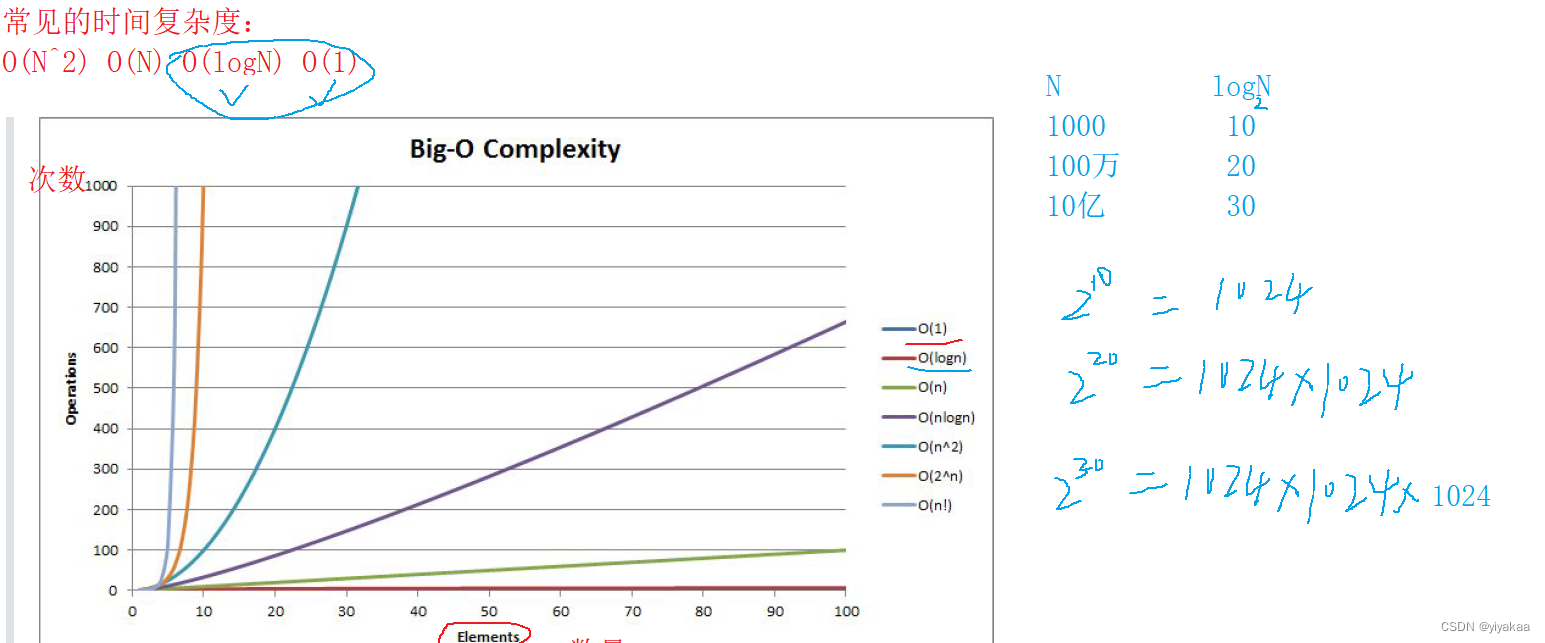
空间复杂度：是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度不是程序占用了多少bytes的空间，所以空间复杂度算的是变量的个数。

问题1：

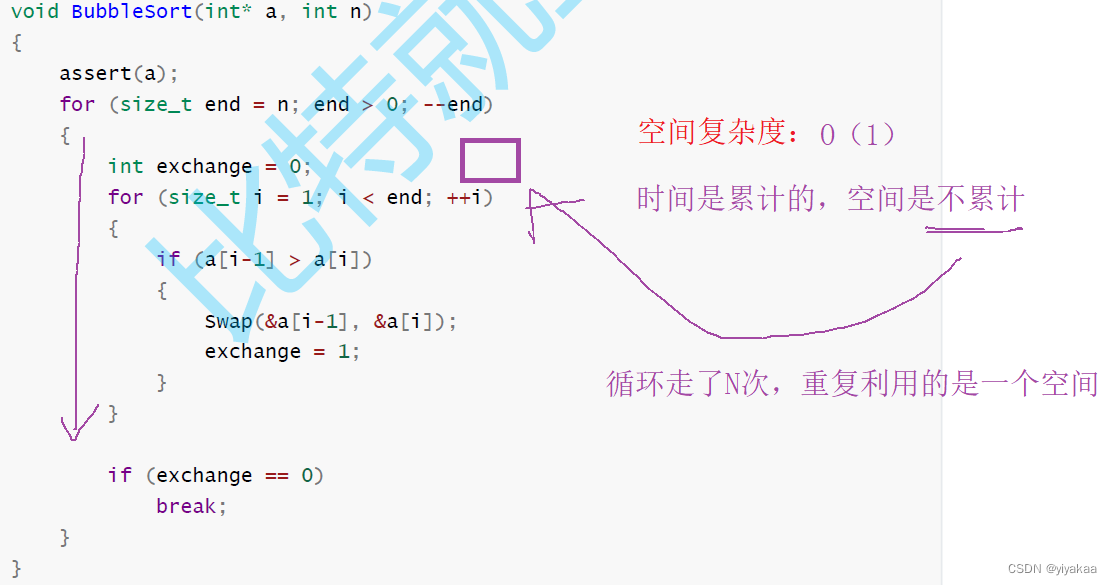
问题2：开辟了n+1个空间

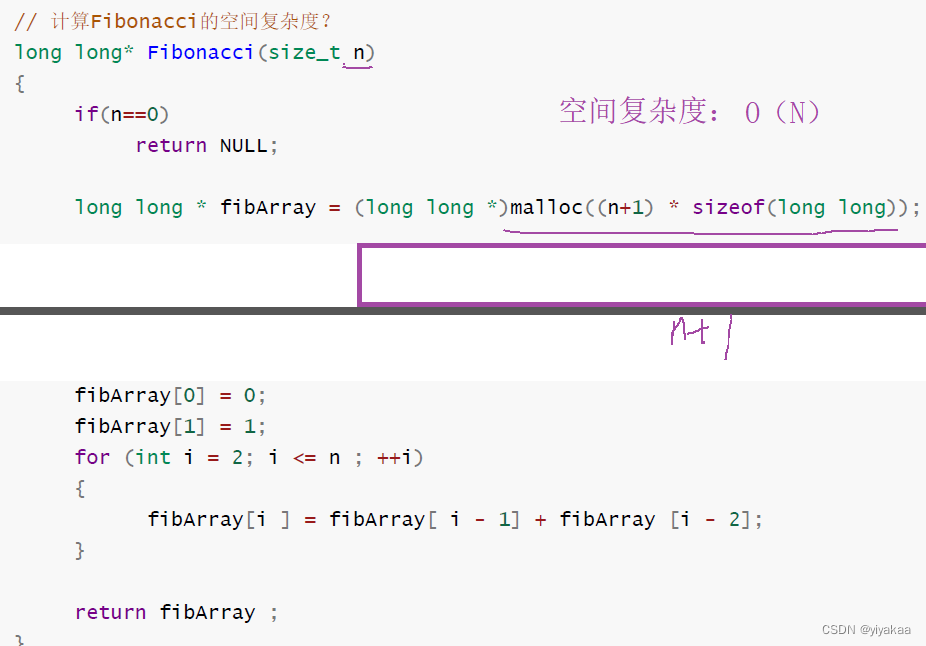
问题3：调用了N层，下去的时候没有销毁，上来的时候才销毁

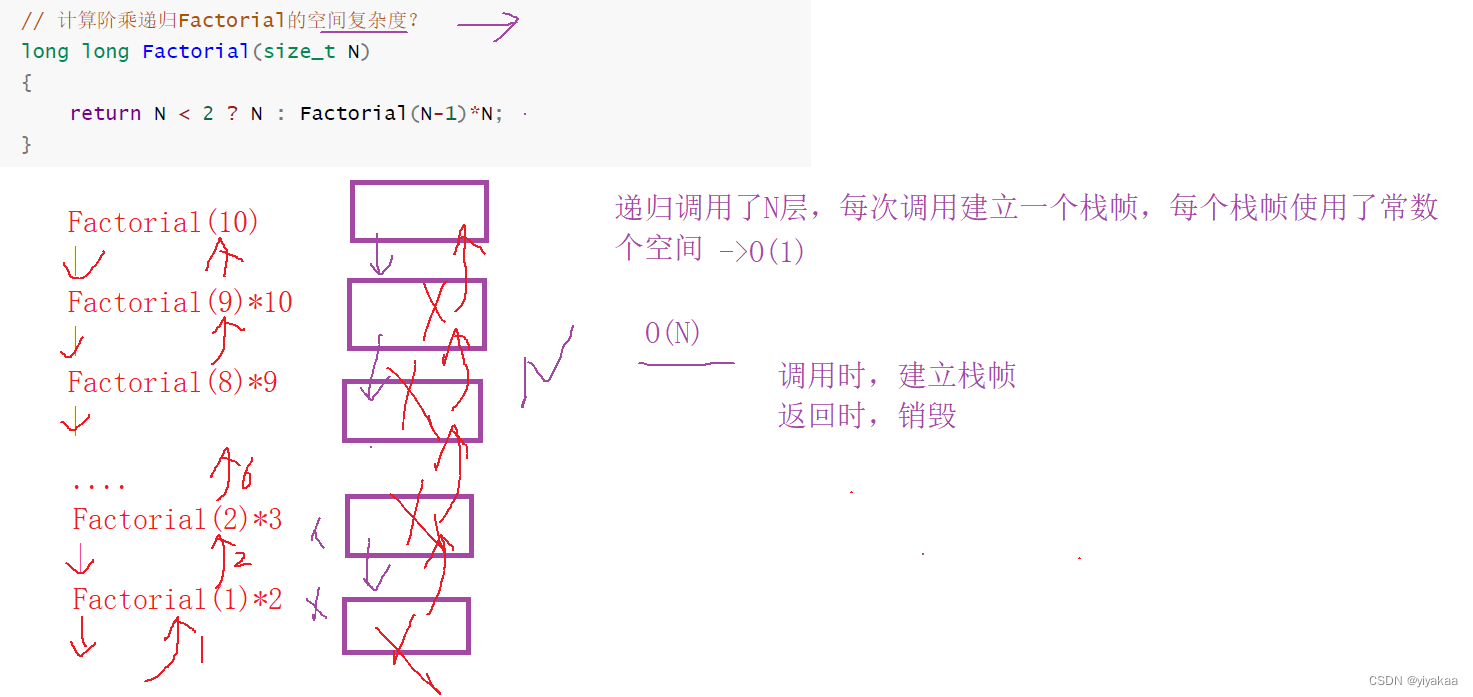
算法1：

数组nums包含从0到n的所有整数，但其中缺了一个，请编写代码找出那个缺失的整数。在O(n)时间内完成
思路一：把0-n加到一起结果是ret1，再把数组中数加到一起ret2，ret1-ret2就是要找的数。
思路二：数组中数依次跟0-N的所有异或，最后剩下的数据就是缺的那个数字
（按位异或，相同为0，相异为1），

int search(int arr[],int len) {
	int x = 0;
	for (int i = 0; i < len;i++) {
		x ^= arr[i];
	}
	for (int j = 0; j < len + 1; j++) {
		x ^= j;
	}
	return x;
}
int main() {
	int arr[] = {9,6,4,2,3,5,7,0,1};
	int len = sizeof(arr) / sizeof(arr[0]);
	int ret = search(arr, len);
	printf("%d\n", ret);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

算法2：

旋转数组：给定一个数组，将数组中的元素向右移动k个位置，其中k是非负数
输入：nums = [1,2,3,4,5,6,7], k=3
输出：[5,6,7,1,2,3,4]
向右旋转1步：[7,1,2,3,4,5,6]
向右旋转2步：[6,7,1,2,3,4,5]
向右旋转3步：[5,6,7,1,2,3,4]

思路1：但是这种方法给一个大数组通不过测试用例

int* search(int arr[],int len,int k) {
	int* x = arr;
	for (int i = 0; i < k;i++) {
		int tmp = arr[len - 1];
		for (int end = len - 2; end >= 0; end--) {
			arr[end + 1] = arr[end];
		}
		arr[0] = tmp;
	}
	return x;
}
int main() {
	int arr[] = {1,2,3,4,5,6,7};
	int k = 3;
	int len = sizeof(arr) / sizeof(arr[0]);
	int* ret = search(arr, len, k);
	for (int i = 0; i < len; i++) {
		printf("%d ", ret[i]);
	}
	return 0;
}

//可以不用传回来值，因为是传址的

void search(int arr[], int len, int k) {

	for (int i = 0; i < k; i++) {
		int tmp = arr[len - 1];
		for (int end = len - 2; end >= 0; end--) {
			arr[end + 1] = arr[end];
		}
		arr[0] = tmp;
	}
}
int main() {
	int arr[] = { 1,2,3,4,5,6,7 };
	int k = 3;
	int len = sizeof(arr) / sizeof(arr[0]);
	search(arr, len, k);
	for (int i = 0; i < len; i++) {
		printf("%d ", arr[i]);
	}
	return 0;
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

思路2：三次逆置解决问题

void search(int arr[],int left,int right) {
	while (left<right) {
		int tmp = arr[right];
		arr[right] = arr[left];
		arr[left] = tmp;
		left++;
		right--;
	}
}
int main() {
	int arr[] = { 1,2,3,4,5,6,7 };
	int k = 3;
	int len = sizeof(arr) / sizeof(arr[0]);
	search(arr,0,len-k-1);
	search(arr, len-k, len - 1);
	search(arr, 0, len - 1);
	for (int i = 0; i < len; i++) {
		printf("%d ", arr[i]);
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21