Halcon中旋转、标定、位姿矩阵的说明_vectortohommat2d

旋转矩阵

对于视觉算法工程师而言，理解矩阵的数学,物理原理十分重要，大多数人对矩阵的理解仅限于解析数学公式上面，其实这跟国内的线性代数教材有关，推荐大家去网上找麻省理工的线性代数公开课看看，从物理应用的角度去讲线性代数，相信你会有更对的收获。本篇博客主要讲解halcon中牵扯到的旋转矩阵说明，也有助于大家理解仿射变换，坐标系转换，标定等等。

Halcon中的HomMat2D

在halcon中牵扯到矩阵转换的有两个方面，在一个坐标系内旋转变换（仿射变换），在两个坐标系之间的转换。

vector_angle_to_rigid (0,0,0,5,5,rad(30), HomMat2D)
1

这里就代表一个坐标系（在halcon中就是对某个图像的像素坐标系旋转等做变换），像素坐标系的原点从（0，0）平移到了（5，5），同时坐标系一开始与水平方向的夹角是0度，逆时针旋转了30度。

打开halcon的数据窗口，观察这时候的HomMat2D的值可以看到

这里便是我们常见的旋转和平移的齐次坐标矩阵。这里的5是0到5的相对平移。

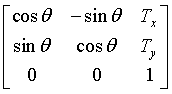
那这个旋转矩阵在halcon中怎么用呢？我用以下几个例子说明帮助大家理解。

vector_angle_to_rigid (0,0,0,5,5,rad(30), HomMat2D)
affine_trans_image (Image, ImageAffinTrans, HomMat2D, 'constant', 'false')
1
2

这个齐次坐标矩阵使图像发生了旋转和坐标系原点的平移

之前像素坐标系的原点在左上角（0，0）处平移到了（5，5）处，图像逆时针旋转了30度
那么如果是顺时针旋转30度呢？只需要更改下顺序即可

//逆时针30度
vector_angle_to_rigid (0,0,0,5,5,rad(30), HomMat2D)
//顺时针30度
vector_angle_to_rigid (0, 0, rad(30), 5, 5, 0, HomMat2D)
1
2
3
4

那么还有个问题？旋转问题需要确定两点，那就是旋转中心和旋转角度，假如说在当前像素坐标系下我只需要将图像绕某一点旋转，如（300，400）逆时针旋转30度，只需要

vector_angle_to_rigid (300, 400, 0, 300, 400, rad(30), HomMat2D)
1

这样的话，就没有发生相对位移，只有相对旋转了30度
同样的，HomMat2D不仅仅应用在图像的旋转上，还可以对区域，像素点进行旋转

vector_angle_to_rigid (0,0,0,5,5,rad(30), HomMat2D)
//对区域进行转换
affine_trans_region (Region, RegionAffineTrans, HomMat2D, 'nearest_neighbor')
//对像素点进行转换，从（64，64）变换到（QX,QY）
affine_trans_point_2d (HomMat2D, 64, 64, Qx, Qy)
1
2
3
4
5

当然，生成HomMat2D矩阵的算子不只一种，其余还可以生成矩阵的算子有

//生成一个单位矩阵，表示什么也不做
hom_mat2d_identity (HomMat2DIdentity)
//在单位矩阵的基础上增加旋转角度和旋转中心
hom_mat2d_rotate (HomMat2DIdentity, rad(30), 0, 0, HomMat2DRotate)
//在单位矩阵的基础上增加平移，坐标原点从（0，0）到了（1，1）
hom_mat2d_translate (HomMat2DIdentity, 1, 1, HomMat2DTranslate)
1
2
3
4
5
6

以上都是在同一个坐标系下hommat2d矩阵代表的意义。那么从数学的角度如何说明呢？
AX=B
HomMat2D便是X，A是Image，与HomMat2D相乘后变成了ImageAffines
A也可以是区域，也可以是原像素点（1，1）

HomMat2D也可以是两个坐标系之间的关系，这时候 ，HomMat2D便不仅仅是旋转矩阵了，在手眼标定的过程中，利用现有的图像像素坐标点和机器人坐标点，便可以求出HomMat2D

上图是九点标定的示意图，同一个物体，在像素坐标系下是（PX,PY）,在机器人坐标系下是(QX,QY).
同一个物体，在不同的坐标系下坐标数值不同，那么两个坐标系之间的转换关系便是HomMat2D

Px:=[1,2,3,4,5,6,7,8,9]
Py:=[1,2,3,4,5,6,7,8,9]
Qx:=[10,20,30,40,50,60,70,80,90]
Qy:=[10,20,30,40,50,60,70,80,90]
vector_to_hom_mat2d (Px, Py, Qx, Qy, HomMat2D)
1
2
3
4
5

总共有9个点，在像素坐标系下是（1，1），（2，2）…在机器人坐标系下是（10，10），（20，20）…根据已知的9个点，便可以求出来HomMat2D
接下来便可以根据HomMat2D将像素坐标系下的点转换成机器人坐标系下的点

vector_to_hom_mat2d (Px, Py, Qx, Qy, HomMat2D)
//将像素坐标系下的（64，64）转化成机器人坐标系下的（QX1,QY1）
affine_trans_point_2d (HomMat2D, 64, 64, Qx1, Qy1)
1
2
3

这时候的数学原理AX=B
X是HomMat2D,代表两个像素坐标系下的转换矩阵
A代表像素坐标系下的点，B代表机器人坐标系下的点

Halcon中的HomMat3D

同样的，HomMat3D可以是一个像素坐标系下的旋转平移关系，也可以代表两个坐标系之间的关系。不同的是，这时候不是二维坐标系，而是三维坐标系。HomMat2D是3乘3的齐次坐标矩阵，HomMat3D是4*乘4的齐次坐标矩阵。

//生成单位矩阵
hom_mat3d_identity (HomMat3DIdentity)
//在单位矩阵的基础上，绕x轴旋转30度
hom_mat3d_rotate (HomMat3DIdentity, rad(30), 'x', 0, 0, 0, HomMat3DRotate)
1
2
3
4

之前说过，九点标定只是手眼标定中一项，是平面之间的手眼标定，求3D图像和实际3维空间中知道高度信息的物体之间的手眼标定关系，便可以使用

vector_to_hom_mat3d ('rigid', Px, Py, Pz, Qx, Qy, Qz, HomMat3D)
1

Halcon中的位姿pose

在halcon中，两个矩阵之间的转换关系不仅仅可以用HomMat3D表示，也可以用位姿pose表示。具体位姿是什么（欧拉角，旋转方法等…大家自行百度机器人学的内容）

//将齐次坐标系转换为位姿
hom_mat3d_to_pose (HomMat3D, Pose)
//将位姿转换为齐次坐标系
pose_to_hom_mat3d (Pose, HomMat3D)
//更改位姿的表达类型
convert_pose_type (Pose, 'Rp+T', 'gba', 'point', PoseOut)
1
2
3
4
5
6

所以在看Halcon相关手眼标定例程中，有时候用位姿pose表示，有时候用HomMat3D表示，其物理原理是一样的，只不过是数学表达方式不同

这里使用HomMat3D代表的4乘4的齐次坐标矩阵

转化成用Pose表示后，便是6乘1的矩阵类型

结束语

在仿射变换，手眼标定的过程中经常遇到矩阵，结合矩阵的数学原理和Halcon实际的物理变换有助于理解这个过程，对于提高Halcon学习十分重要，大家一定要多仔细研究。