- 1关于jsonobject类型的Null值怎么判断的问题,JSONObject$Null_jsonobject判断null
- 2INTELLIJ IDEA 项目(初始化/删除) GIT_idea删除git信息
- 3逻辑思维训练1200题-蓝桥杯计算思维参考_蓝桥杯计算思维u8
- 4优化算法|遗传算法求解作业车间调度问题(Python)_python实现遗传算法车间调度求解的代码
- 5mysql8 Incorrect datetime value: '0000-00-00 00:00:00'_mysql-connector-java-8.0.22 incorrect datetime val
- 6几道数据结构选择题_数据结构多选题
- 7唯一索引 oracle 空值,pgsql 组合唯一约束或唯一索引 null失效的情况
- 8【米哈游】2024秋招接近尾声,还没投递的抓紧上车啦!_深圳欣锐科技 计算机硕士 知乎
- 9FPGA实现的高效CIC滤波器:内插滤波器与数字信号多采样率处理_高效 数字滤波
- 10解决Win10找不到msvcp140_atomic_wait.dl文件_msvcp140-atomic-wait.dll
【Matlab群体智能算法第二期】基于反向学习的改进粒子群算法(含matlab代码)_粒子群算法改进matlab
赞
踩
0.前言
上一篇文章主要对传统粒子群算法原理及matlab代码进行讲解,该篇文章为上述文章的延续,主要讲述粒子群算法后续变体版本及matlab代码复现。上篇文章链接如下:https://blog.csdn.net/hbdlhy/article/details/130798548?spm=1001.2014.3001.5501
当前针对启发式算法改进主要分为:种群初始化改进、种群更新迭代改进等方向,本期主要讲解种群初始化方向改进策略。
1.传统粒子群算法种群初始化
在传统粒子群算法中,种群位置初始化主要采用随机数的方式,matlab代码如下:
- %N为种群数量;D为例粒子维度
- x=rand(N,D)
上述方式能够为粒子群算法的初始种群提供初始随机位置,但当求解含粒子边界约束的优化问题时,可能导致初始时刻生成的多数粒子种群均不满足边界约束,从而降低算法寻优效率。因此引入边界范围的种群初始化方式被广泛应用于初始种群生成中,其matlab代码如下:
- %含边界约束的种群初始化方式
- %Ub为粒子上界、Lb为粒子下界
- x=Lb+rand(N,D).*(Ub-Lb);
采用上述方式生成初始种群后,能够满足所生成的种群解均满足粒子边界约束,这极大的提升了算法求解含边界约束问题的效率。
2.基于反向学习策略的种群初始化
尽管上述初始化方法能够一定程度上提升粒子群算法的求解效率,但根据概率论相关理论,在没有先验知识优化问题的情况下,相较于引入两个独立的随机解,一个随机解与其对应的反向解更有可能出现在全局最优解附近,因此反向学习策略具有加速算法收敛的潜能。
反向学习策略步骤如下:
(1)生成初始种群解的位置X,如式(1):
(2)根据式(2)生成初始种群X的反向种群,如下所示:
(3)将反向种群与初始种群合并,组成新种群,并依据适应度函数值,取前N个种群作为最终初始化后粒子群算法的初始种群解。其中,N为粒子群算法种群数量。
根据上述步骤,基于反向学习的种群初始化代码如下(matlab):
- function [Best_f,X_new]=OBL_main(N,D,Lb,Ub)
-
- %% 基于反向学习的种群初始化
- % N=30;%种群数量
- % D=3;%粒子维度
-
- %生成随机初始种群
- % Lb=[-5,-5,-5];%种群解的下限
- % Ub=[5,5,5];%种群解的上限
- X=Lb+rand(N,D).*(Ub-Lb);
-
- %生成反向学习种群
- X_obl=rand(N,D).*(Lb+Ub)-X;
-
- %合并种群
- X_total=[X;X_obl];
-
- %根据目标函数值选取最终初始种群
- fit=[];
- for L=1:size(X_total,1)
- fit(1,L)=fitness_obl(X_total(L,:));
- end
-
- %对目标函数值进行升序
- [B,I] = sort(fit);
-
- %获取前N个适应度函数值最优的种群为反向学习后的最终初始种群
- Best_x=I(1,1:N);
- Best_f=B(1,1:N);
- X_new=X_total(Best_x,:);
(反向学习策略代码与2024年1月16日更新,原版代码生成反向种群时误写成(Lb-Ub),现已经改正,抱歉!)
3.基于反向学习的粒子群算法
结合第2部分反向学习内容,现将反向学习策略与粒子群算法相结合,具体代码如下:
- %% 基于反向学习策略的改进粒子群算法主程序
- clc;
- clear all;
- close all
- %% 算法基本参数设置
- c1=2; %学习因子1
- c2=2;%学习因子2
- w=0.7;%惯性权重
- MaxDT=500;%最大迭代次数
- D=3;%搜索空间维数(未知数个数)
- N=30;%初始化群体个体数目
- Lb=[-100,-100,-100];%种群解的下限
- Ub=[100,100,100];%种群解的上限
- Vmax=[1,1,1];%速度上限
- Vmin=[-1,-1,-1];%速度下限
-
- %% 基于反向学习策略的种群初始化
- [Best_f,pop]=OBL_main(N,D,Lb,Ub);
- V=rand(N,D);
- %计算各个粒子的适应度值并初始化Pi和Pg
- [fitnessgbest bestindex]=min(Best_f);
- gbest=pop(bestindex,:);
- pbest=pop;
- fitnesspbest=Best_f;
-
- %% 粒子群算法更新迭代部分
- for i=1:MaxDT
- for j=1:N
- %种群更新
- V(j,:)=w*V(j,:)+c1*rand*(pbest(j,:)-pop(j,:))+c2*rand*(gbest-pop(j,:));
- %更新速度边界检查
- I=V(j,:)<Vmin;
- V(j,I)=Vmin(I);
- U=V(j,:)>Vmax;
- V(j,U)=Vmax(U);
- pop(j,:)=pop(j,:)+V(j,:);
- %粒子边界检查
- PI=pop(j,:)<Lb;
- pop(j,PI)=Lb(PI);
- PU=pop(j,:)>Ub;
- pop(j,PU)=Ub(PU);
- %计算更新后种群的适应度函数值
- Best_f(j)=fitness_obl(pop(j,:));
-
- %个体极值更新
- if Best_f(j)<fitnesspbest(j)
- pbest(j,:)=pop(j,:);
- fitnesspbest(j)=Best_f(j);
- end
-
- %全局极值更新
- if Best_f(j)<fitnessgbest
- gbest=pop(j,:);
- fitnessgbest=Best_f(j);
- end
-
- end
- %记录粒子全局最优解
- Fgbest(i)=fitnessgbest;
-
- end
- %% 结果可视化
- figure
- plot(Fgbest)
- title(['适应度曲线 ' '终止次数=' num2str(MaxDT)]);
- xlabel('进化代数');
- ylabel('适应度')
其中目标函数fitness_obl的matlab代码如下:
- function f=fitness_obl(x)
-
- f=sum((x+0.5).^2);
4.改进后寻优结果对比
本次测试采用fitness_obl目标函数进行,大家也可自行尝试采用其他目标函数,算法在不同目标函数下所呈现的寻优能力有一定差别。测试过程中分别对该目标函数运行10次,并记录算法改进前后最好、最差及目标函数的均值,具体结果如下:
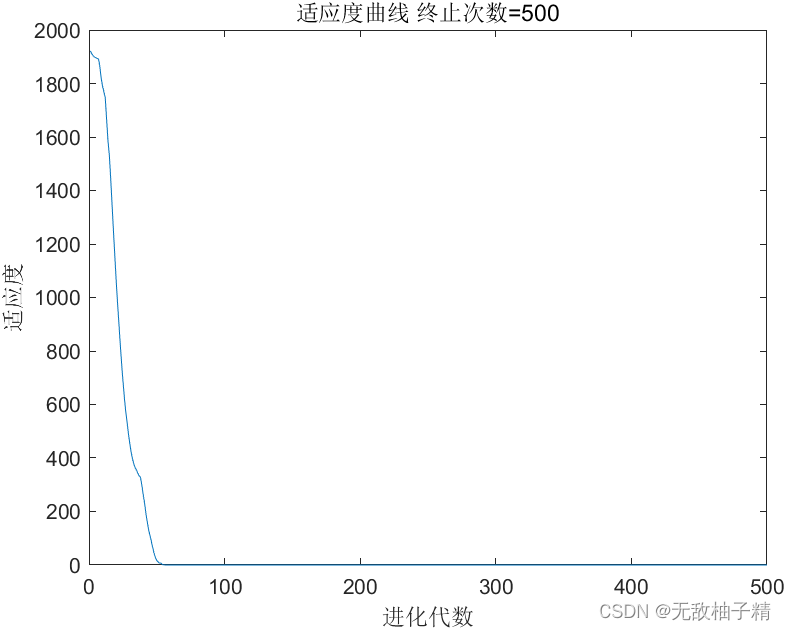
图1 基于反向学习的粒子群算法适应度曲线
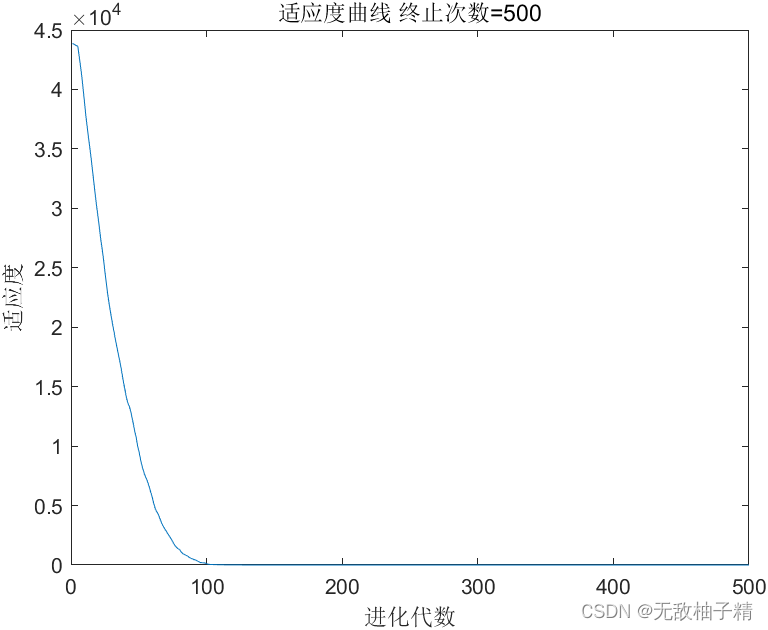
图2标准粒子群算法适应度曲线
从上述第二代曲线能够看出,采用反向学习后,粒子群算法的收敛速度更快,求解效率更高,能够通过更少的迭代步骤实现更高精度的求解。在该迭代过程中,基于反向学习的粒子群算法最优适应度值为3.3588*e-31,而标准粒子群算法的最有适应度值为0.0831。由此可见改进后算法的寻优能力更好,收敛速度更快。
为了进一步证明改进后算法的稳定性及寻优结果的可靠性,分别对算法改进前后运行10次,结果如下:
| 运行次数 | 基于反向学习改进后 | 标准粒子群算法 |
| 1 | 3.36E-31 | 0.0831 |
| 2 | 1.82E-29 | 0.0547 |
| 3 | 1.85E-32 | 0.0294 |
| 4 | 2.74E-29 | 0.0119 |
| 5 | 3.08E-33 | 0.0477 |
| 6 | 2.28E-29 | 0.0399 |
| 7 | 7.67E-31 | 0.0459 |
| 8 | 2.90E-31 | 0.0235 |
| 9 | 1.26E-31 | 0.0043 |
| 10 | 1.39E-31 | 0.0532 |
| 均值 | 7.01E-30 | 0.03936 |
| 最小值 | 3.08149E-33 | 0.0043 |
| 最大值 | 2.73883E-29 | 0.0831 |
根据上述结果可知,采用反向学习策略后,能够较好的提升粒子群算法的寻优能力及寻优精度,提升算法求解效率。
5.后续改进
本部分仅对种群初始化部分进行介绍,后续该部分将继续对对立学习策略、混沌映射等改进策略进行讲解。在种群更行迭代部分,对t分布自适应变异、Levy飞行策略等改进方法进行讲解,感谢大家耐心阅读,本文代码改进部分均为作者自身复现,谢绝转载,严禁以此进行二次售卖。
作者主要更新方向为:
(1)智能算法复现及改进;
(2)微电网/综合能源系统容量配置、优化调度等方向
(3)时间序列预测(机器学习、深度学习方向)
欢迎大家相互交流,另作者水平有限,难免存在疏忽之处,若有错误请大家指正,谢谢。


