决策树C4.5算法

决策树-C4.5

前面的ID3算法已经介绍了决策树的基本概念。C4.5算法在ID3算法上做了提升，使用信息增益比来构造决策树，且有剪枝功能防止过拟合，本模块将以C4.5算法介绍决策树的构造策略。

欠拟合：训练得到的模型在训练集集测试中表现就很差，准确度很低。
过拟合：训练得到的模型在训练集表现很好，但在测试集表现很差。

信息增益比：特征A对训练集D的信息增益比定义为特征A的信息增益与训练集D对于A的信息熵之比。
$$信息增益比Gain（D,A）=\frac{info（D,A）}{H(D,A)}$$

公式在ID3算法中

剪枝：在决策树对训练集的预测误差和数的复杂度之间找到一个平衡。剪枝算法的功能是输入生成的决策树和参数，输出剪枝后的决策树。包括先剪枝和后剪枝。

1. 先剪枝：提前停止树的构建而对树”剪枝“，提前停止的策略有定义一个树的深度，到达指定深度自动停止构造；
2. 后剪枝：先构造完整的子树，对于决策树中那些置信度不够（信息增益比较低）的子树用叶子节点（类别）代替。

决策树构造策略

1. 计算训练集得出每个特征的信息增益比
2. 选取当下的最大信息增益比的特征作为决策树头节点，由该特征的不同属性划分为不同子树
3. 去除该特征后计算在满足该属性的情况下剩下的N个特征的信息增益比，并继续划分子树
4. 据此递归所有特征划分完成，每个子树结束后都有对应类别。

以图中西瓜数据集（D）描述构造决策树原理

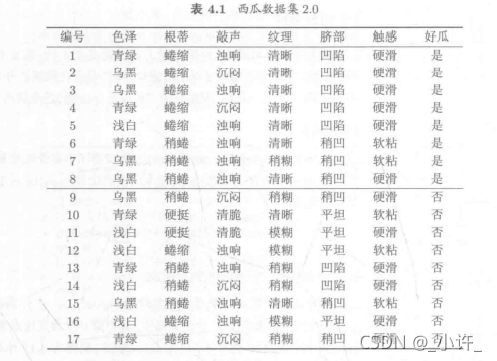
根据公式计算个特征的信息增益：info(D,色泽)=0.109 ，info(D,根蒂)=0.143，info(D,敲声)=0.141，info(D，纹理)=0.381，info(D,脐部)=0.289，info(D,触感)=0.006

再计算信息增益比:$$Gain(D,色泽)=\frac{info（D，色泽）}{H(D,色泽)}=\frac{info(D,色泽)}{-(\frac{6}{17}{\log }_2\frac{6}{17}+\frac{6}{17}{\log }_2\frac{5}{17}+\frac{5}{17}{\log }_2\frac{5}{17})}=0.069$$

再计算其他的值Gain（D，根蒂）=0.046，Gain（D，敲声）=0.051，Gain（D，纹理）=0.043，Gain（D，脐部）=0.072，Gain（D，触感）=0.028

第一次计算可知Gain(D,肚部)=0.072最大作为决策树根节点，构造决策树：

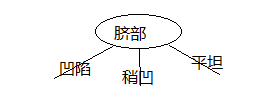
然后再脐部凹陷，脐部稍凹，脐部平坦的条件下再计算除脐部外的其他特征的信息增益比，继续递归构造子树。

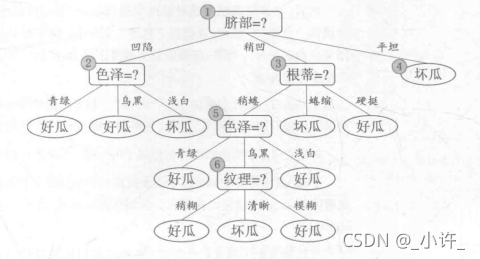
C4.5算法实现构造决策树：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import tree  #导入树库可视化决策树
from sklearn.tree import DecisionTreeClassifier   #导入决策树模型

#加载数据集
iris=load_iris()

#划分数据集和测试集
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,test_size=0.3)

#构造决策树模型
decision_tree=DecisionTreeClassifier(criterion="entropy",max_depth=5)  #criterionz指定节点特征选择基准entropy是ID3,c4.5;gini是CART算法 #decision_tree是常用的剪枝参数

#训练决策树
decision_tree=decision_tree.fit(x_train,y_train)

score=decision_tree.score(x_test,y_test)
print(score)
结果：
0.8666666666666667

可视化决策树：
print(tree.plot_tree(decision_tree))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// graphviz 库可视化树
import graphviz    
graph = tree.export_graphviz(decision_tree, out_file=None)
graph = graphviz.Source(graph)
graph
1
2
3
4
5