时序预测 | Transformer时间序列预测 Matlab代码_matlab实现transformer预测

---

效果一览

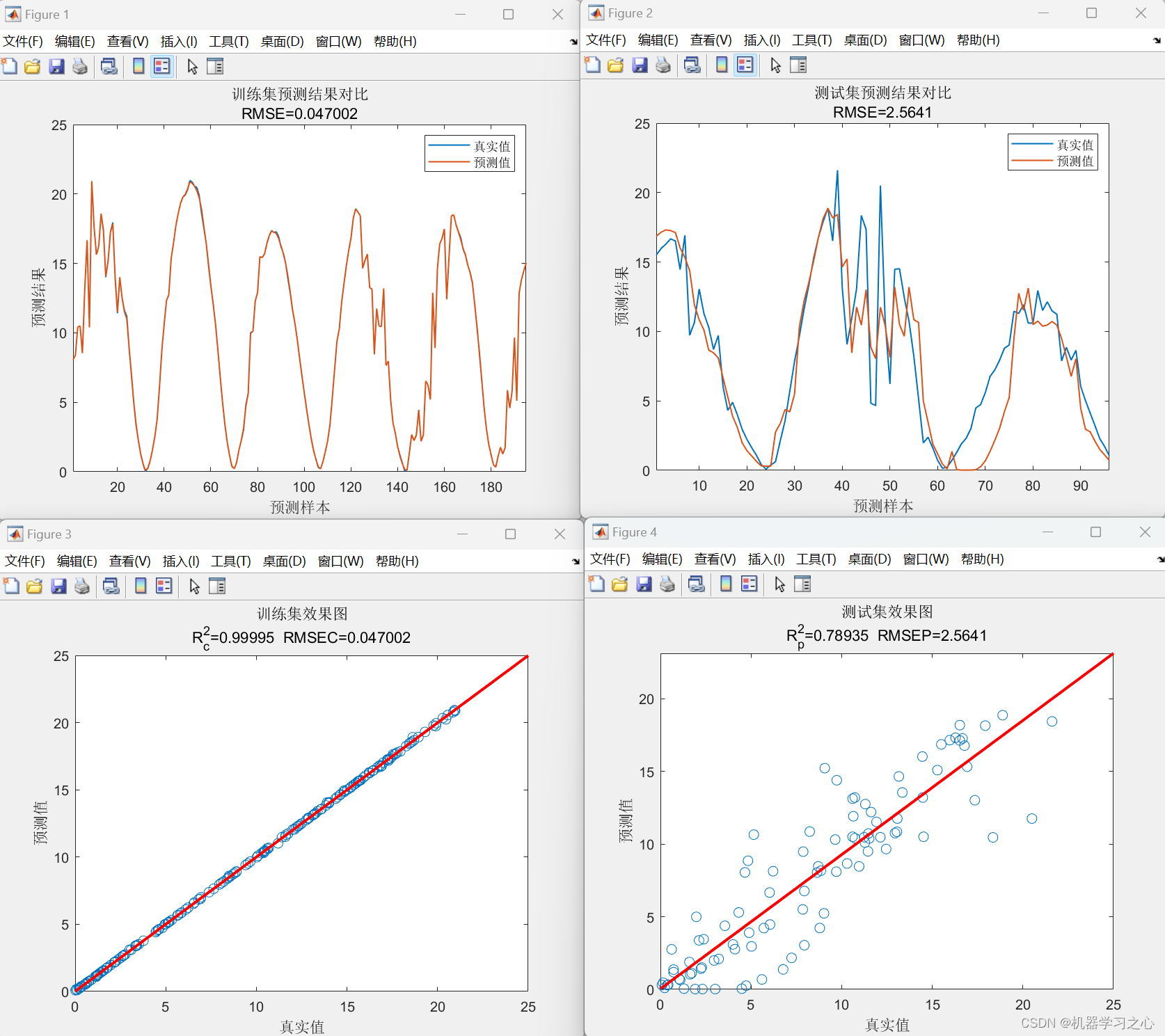
文章概述

1.时序预测 | Transformer时间序列预测 Matlab代码
2.单变量时间序列预测；
3.多指标评价，评价指标包括：R2、MAE、MBE等，代码质量极高；
4.excel数据，方便替换，运行环境2020及以上。
长期以来，时间序列预测一直使用统计方法（例如，自回归综合移动平均（ARIMA，指数平滑和结构模型）。一般来说，统计方法中使用的参数模型需要大量的领域专业知识来构建。为了减轻这种负担，许多机器学习技术，如梯度推进回归树（gradient boosting Retression tree，GBRT）得到了应用，它以数据驱动的方式学习时间序列的时间动态。然而，这些方法仍然需要手动特征工程和模型设计。深度神经网络（DNN）可以子鄂东从大量数据中获得的强大表示学习能力，出现了各种基于深度学习的TSF解决方案，在许多情况下取得了比传统技术更好的预测精度。
基于递归神经网络（RNN）的方法和基于卷积神经网络（CNN）的方法也被应用到TSF任务上。基于RNN的TSF方法属于迭代多步（IMS）预测。根据解码器是否以自回归方式实现，基于CNN的TSF方法即存在迭代多步（IMS）预测技术，也存在直接多步骤（DMS）预测技术。
Transformer可以说是最成功的序列建模架构，它在各种人工智能应用中表现出无与伦比的性能，如自然语言处理、语音识别和运动分析。最近，出现了很多基于Transformer的时间序列分析的工作。其中TSF任务的一些优秀的工作包括：LogTrans（NeurIPS 2019），Informer（AAAI 2021最佳论文），Autoformer（NeurIPS 2021），Pyraformer（ICLR 2022 ORAL），以及最近的FEDformer（ICML 2022)。

源码设计

%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% CSDN博主机器学习之心
%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  数据集分析
outdim = 1;                                  % 最后一列为输出
             % 输入特征维度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);

%save BP T_train T_test T_sim1 T_sim2
%%  相关指标计算
%  R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test  - T_sim2)^2 / norm(T_test  - mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

%  MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;
mae2 = sum(abs(T_sim2 - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));

disp(['训练集数据的MAPE为：', num2str(MAPE1)])
disp(['测试集数据的MAPE为：', num2str(MAPE2)])

%  MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;
mbe2 = sum(T_sim2 - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

%均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;

disp(['训练集数据的MSE为：', num2str(mse1)])
disp(['测试集数据的MSE为：', num2str(mse2)])


%%  绘图
figure
plot(1: M, T_train, '-', 1: M, T_sim1, '-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])


figure
plot(1: N, T_test, '-', 1: N, T_sim2, '-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])

%% 绘制线性拟合图
%% 训练集拟合效果图
figure
plot(T_train,T_sim1,'o','Markersize',7);
xlabel('真实值')
ylabel('预测值')
string = {'训练集效果图';['R^2_c=' num2str(R1)  '  RMSEC=' num2str(error1) ]};
title(string)
hold on ;h=lsline;
set(h,'LineWidth',2,'LineStyle','-','Color',[1 0 0])
%% 预测集拟合效果图
figure
plot(T_test,T_sim2,'o','Markersize',7);
xlabel('真实值')
ylabel('预测值')
string1 = {'测试集效果图';['R^2_p=' num2str(R2)  '  RMSEP=' num2str(error2) ]};
title(string1)
hold on ;h=lsline();

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115

参考资料

[1] Eric A. Wan, Rudolph van der Merwe. The Unscented Kalman Filter for Nonlinear Estimation. Oregon Graduate Institute of Science & Technology, Feb 2000
[2] carbon_emission_prediction_and_forecast