Practical Lessons from Predicting Clicks on Ads at Facebook

 

Xinran He, Junfeng Pan, Ou Jin, Tianbing Xu, Bo Liu ⇤ , Tao Xu ⇤ , Yanxin Shi ⇤ ,
Antoine Atallah ⇤ , Ralf Herbrich ⇤ , Stuart Bowers, Joaquin Quiñonero Candela
Facebook
1601 Willow Road, Menlo Park, CA, United States
{panjunfeng, oujin, joaquinq, sbowers}@fb.com

---

ABSTRACT

Online advertising allows advertisers to only bid and pay for measurable user responses, such as clicks on ads. As a consequence, click prediction systems are central to most on-
line advertising systems. With over 750 million daily active users and over 1 million active advertisers, predicting clicks on Facebook ads is a challenging machine learning task. In this paper we introduce a model which combines decision
trees with logistic regression, outperforming either of these methods on its own by over 3%, an improvement with sig-nificant impact to the overall system performance. We then
explore how a number of fundamental parameters impact the final prediction performance of our system. Not surpris-ingly, the most important thing is to have the right features:
those capturing historical information about the user or ad dominate other types of features. Once we have the right features and the right model (decisions trees plus logistic re-gression), other factors play small roles (though even small improvements are important at scale). Picking the optimal handling for data freshness, learning rate schema and data sampling improve the model slightly, though much less than adding a high-value feature, or picking the right model to begin with.

1. INTRODUCTION

 

Digital advertising is a multi-billion dollar industry and is
growing dramatically each year. In most online advertising
platforms the allocation of ads is dynamic, tailored to user
interests based on their observed feedback. Machine learn-
ing plays a central role in computing the expected utility
of a candidate ad to a user, and in this way increases the
⇤ BL works now at Square, TX and YS work now at Quora,
AA works in Twitter and RH works now at Amazon.
Permission to make digital or hard copies of all or part of
this work for personal or classroom use is granted without
fee provided that copies are not made or distributed for
profit or commercial advantage and that copies bear this
notice and the full citation on the first page. Copyrights for
components of this work owned by others than ACM must
be honored. Abstracting with credit is permitted. To copy
otherwise, or republish, to post on servers or to redistribute
to lists, requires prior specific permission and/or a fee.
Request permissions from Permissions@acm.org.
ADKDD’14, August 24 - 27 2014, New York, NY, USA
Copyright 2014 ACM 978-1-4503-2999-6/14/08$15.00.
http://dx.doi.org/10.1145/2648584.2648589
e?ciency of the marketplace.
The 2007 seminal papers by Varian [11] and by Edelman et
al. [4] describe the bid and pay per click auctions pioneered
by Google and Yahoo! That same year Microsoft was also
building a sponsored search marketplace based on the same
auction model [9]. The e?ciency of an ads auction depends
on the accuracy and calibration of click prediction. The
click prediction system needs to be robust and adaptive, and
capable of learning from massive volumes of data. The goal
of this paper is to share insights derived from experiments
performed with these requirements in mind and executed
against real world data.
In sponsored search advertising, the user query is used to
retrieve candidate ads, which explicitly or implicitly are
matched to the query. At Facebook, ads are not associated
with a query, but instead specify demographic and interest
targeting. As a consequence of this, the volume of ads that
are eligible to be displayed when a user visits Facebook can
be larger than for sponsored search.
In order tackle a very large number of candidate ads per
request, where a request for ads is triggered whenever a user
visits Facebook, we would first build a cascade of classifiers
of increasing computational cost. In this paper we focus on
the last stage click prediction model of a cascade classifier,
that is the model that produces predictions for the final set
of candidate ads.
We find that a hybrid model which combines decision trees
with logistic regression outperforms either of these methods
on their own by over 3%. This improvement has significant
impact to the overall system performance. A number of
fundamental parameters impact the final prediction perfor-
mance of our system. As expected the most important thing
is to have the right features: those capturing historical in-
formation about the user or ad dominate other types of fea-
tures. Once we have the right features and the right model
(decisions trees plus logistic regression), other factors play
small roles (though even small improvements are important
at scale). Picking the optimal handling for data freshness,
learning rate schema and data sampling improve the model
slightly, though much less than adding a high-value feature,
or picking the right model to begin with.
We begin with an overview of our experimental setup in Sec-
tion 2. In Section 3 we evaluate di↵erent probabilistic linear
classifiers and diverse online learning algorithms. In the con-
text of linear classification we go on to evaluate the impact
of feature transforms and data freshness. Inspired by the
practical lessons learned, particularly around data freshness
and online learning, we present a model architecture that in-
corporates an online learning layer, whilst producing fairly
compact models. Section 4 describes a key component re-
quired for the online learning layer, the online joiner, an
experimental piece of infrastructure that can generate a live
stream of real-time training data.
Lastly we present ways to trade accuracy for memory and
compute time and to cope with massive amounts of training
data. In Section 5 we describe practical ways to keep mem-
ory and latency contained for massive scale applications and
in Section 6 we delve into the tradeo↵ between training data
volume and accuracy.

2. EXPERIMENTAL SETUP

In order to achieve rigorous and controlled experiments, we
prepared o✏ine training data by selecting an arbitrary week
of the 4th quarter of 2013. In order to maintain the same
training and testing data under di↵erent conditions, we pre-
pared o✏ine training data which is similar to that observed
online. We partition the stored o✏ine data into training and
testing and use them to simulate the streaming data for on-
line training and prediction. The same training/testing data
are used as testbed for all the experiments in the paper.
Evaluation metrics: Since we are most concerned with
the impact of the factors to the machine learning model,
we use the accuracy of prediction instead of metrics directly
related to profit and revenue. In this work, we use Normal-
ized Entropy (NE) and calibration as our major evaluation
metric.
Normalized Entropy or more accurately, Normalized Cross-
Entropy is equivalent to the average log loss per impression
divided by what the average log loss per impression would
be if a model predicted the background click through rate
(CTR) for every impression. In other words, it is the pre-
dictive log loss normalized by the entropy of the background
CTR. The background CTR is the average empirical CTR
of the training data set. It would be perhaps more descrip-
tive to refer to the metric as the Normalized Logarithmic
Loss. The lower the value is, the better is the prediction
made by the model. The reason for this normalization is
that the closer the background CTR is to either 0 or 1, the
easier it is to achieve a better log loss. Dividing by the en-
tropy of the background CTR makes the NE insensitive to
the background CTR. Assume a given training data set has
N examples with labels y i 2 {?1,+1} and estimated prob-
ability of click p i where i = 1,2,...N. The average empirical
CTR as p

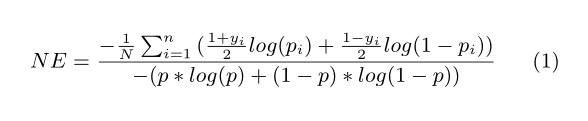
NE is essentially a component in calculating Relative Infor-mation Gain (RIG) and RIG = 1 - NE

Figure 1: Hybrid model structure. Input features
are transformed by means of boosted decision trees.
The output of each individual tree is treated as a
categorical input feature to a sparse linear classifier.
Boosted decision trees prove to be very powerful
feature transforms.

 Calibration is the ratio of the average estimated CTR and
empirical CTR. In other words, it is the ratio of the number
of expected clicks to the number of actually observed clicks.
Calibration is a very important metric since accurate and
well-calibrated prediction of CTR is essential to the success
of online bidding and auction. The less the calibration di↵ers
from 1, the better the model is. We only report calibration
in the experiments where it is non-trivial.
Note that, Area-Under-ROC (AUC) is also a pretty good
metric for measuring ranking quality without considering
calibration. In a realistic environment, we expect the pre-
diction to be accurate instead of merely getting the opti-
mal ranking order to avoid potential under-delivery or over-
delivery. NE measures the goodness of predictions and im-
plicitly reflects calibration. For example, if a model over-
predicts by 2x and we apply a global multiplier 0.5 to fix
the calibration, the corresponding NE will be also improved
even though AUC remains the same. See [12] for in-depth
study on these metrics.

3. PREDICTION MODEL STRUCTURE

In this section we present a hybrid model structure: the
concatenation of boosted decision trees and of a probabilis-
tic sparse linear classifier, illustrated in Figure 1. In Sec-
tion 3.1 we show that decision trees are very powerful input
feature transformations, that significantly increase the ac-
curacy of probabilistic linear classifiers. In Section 3.2 we
show how fresher training data leads to more accurate pre-
dictions. This motivates the idea to use an online learning
method to train the linear classifier. In Section 3.3 we com-
pare a number of online learning variants for two families of
probabilistic linear classifiers.
The online learning schemes we evaluate are based on the
Stochastic Gradient Descent (SGD) algorithm [2] applied to
sparse linear classifiers. After feature transformation, an
ad impression is given in terms of a structured vector x =
(e i 1 ,...,e i n ) where e i is the i-th unit vector and i 1 ,...,i n
are the values of the n categorical input features. In the
training phase, we also assume that we are given a binary
label y 2 {+1,?1} indicating a click or no-click.
Given a labeled ad impression (x,y), let us denote the linear
combination of active weights as

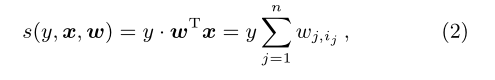
 where w is the weight vector of the linear click score.
In the state of the art Bayesian online learning scheme for
probit regression (BOPR) described in [7] the likelihood and
prior are given by

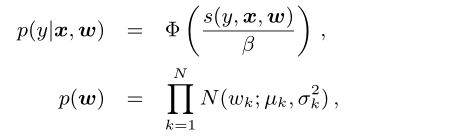
 where ?(t) is the cumulative density function of standard
normal distribution and N(t) is the density function of the
standard normal distribution. The online training is achieved
through expectation propagation with moment matching.
The resulting model consists of the mean and the variance
of the approximate posterior distribution of weight vector
w. The inference in the BOPR algorithm is to compute
p(w|y,x) and project it back to the closest factorizing Gaus-
sian approximation of p(w). Thus, the update algorithm
can be solely expressed in terms of update equations for all
means and variances of the non-zero components x (see [7]):

 Here, the corrector functions v and w are given by v(t) :=
N(t)/?(t) and w(t) := v(t)·[v(t)+t]. This inference can be
viewed as an SGD scheme on the belief vectors µ and ?.
We compare BOPR to an SGD of the likelihood function

 where sigmoid(t) = exp(t)/(1 + exp(t)). The resulting al-
gorithm is often called Logistic Regression (LR). The infer-
ence in this model is computing the derivative of the log-
likelihood and walk a per-coordinate depending step size in
the direction of this gradient:

 

 where g is the log-likelihood gradient for all non-zero com-
ponents and given by g(s) := [y(y + 1)/2 ? y · sigmoid(s)].
Note that (3) can be seen as a per-coordinate gradient de-
scent like (6) on the mean vector µ where the step-size ⌘ i j
is automatically controlled by the belief uncertainty ?. In
Subsection 3.3 we will present various step-size functions ⌘
and compare to BOPR.
Both SGD-based LR and BOPR described above are stream
learners as they adapt to training data one by one.

3.1 Decision tree feature transforms

 

There are two simple ways to transform the input features
of a linear classifier in order to improve its accuracy. For
continuous features, a simple trick for learning non-linear
transformations is to bin the feature and treat the bin in-
dex as a categorical feature. The linear classifier e↵ectively
learns a piece-wise constant non-linear map for the feature.
It is important to learn useful bin boundaries, and there are
many information maximizing ways to do this.
The second simple but e↵ective transformation consists in
building tuple input features. For categorical features, the
brute force approach consists in taking the Cartesian prod-
uct, i.e. in creating a new categorical feature that takes
as values all possible values of the original features. Not
all combinations are useful, and those that are not can be
pruned out. If the input features are continuous, one can do
joint binning, using for example a k-d tree.
We found that boosted decision trees are a powerful and very
convenient way to implement non-linear and tuple transfor-
mations of the kind we just described. We treat each indi-
vidual tree as a categorical feature that takes as value the
index of the leaf an instance ends up falling in. We use 1-
of-K coding of this type of features. For example, consider
the boosted tree model in Figure 1 with 2 subtrees, where
the first subtree has 3 leafs and the second 2 leafs. If an
instance ends up in leaf 2 in the first subtree and leaf 1 in
second subtree, the overall input to the linear classifier will
be the binary vector [0,1,0,1,0], where the first 3 entries
correspond to the leaves of the first subtree and last 2 to
those of the second subtree. The boosted decision trees we
use follow the Gradient Boosting Machine (GBM) [5], where
the classic L 2 -TreeBoost algorithm is used. In each learn-
ing iteration, a new tree is created to model the residual
of previous trees. We can understand boosted decision tree
based transformation as a supervised feature encoding that
converts a real-valued vector into a compact binary-valued
vector. A traversal from root node to a leaf node represents
a rule on certain features. Fitting a linear classifier on the
binary vector is essentially learning weights for the set of
rules. Boosted decision trees are trained in a batch manner.
We carry out experiments to show the e↵ect of including tree
features as inputs to the linear model. In this experiment
we compare two logistic regression models, one with tree fea-
ture transforms and the other with plain (non-transformed)
features. We also use a boosted decision tree model only for
comparison. Table 1 shows the results.
Tree feature transformations help decrease Normalized En-
tropy by more more than 3.4% relative to the Normalized
Entropy of the model with no tree transforms. This is a
very significant relative improvement. For reference, a typ-
ical feature engineering experiment will shave o↵ a couple
of tens of a percent of relative NE. It is interesting to see 
that the LR and Tree models used in isolation have compa-
rable prediction accuracy (LR is a bit better), but that it is
their combination that yield an accuracy leap. The gain in
prediction accuracy is significant; for reference, the majority
of feature engineering experiments only manage to decrease
Normalized Entropy by a fraction of a percentage.

 3.2 Data freshness

 Click prediction systems are often deployed in dynamic envi-
ronments where the data distribution changes over time. We
study the e↵ect of training data freshness on predictive per-
formance. To do this we train a model on one particular day
and test it on consecutive days. We run these experiments
both for a boosted decision tree model, and for a logisitic
regression model with tree-transformed input features.
In this experiment we train on one day of data, and evaluate
on the six consecutive days and compute the normalized
entropy on each. The results are shown on Figure 2.
Prediction accuracy clearly degrades for both models as the
delay between training and test set increases. For both mod-
els it can been seen that NE can be reduced by approxi-
mately 1% by going from training weekly to training daily.
These findings indicate that it is worth retraining on a daily
basis. One option would be to have a recurring daily job that
retrains the models, possibly in batch. The time needed to
retrain boosted decision trees varies, depending on factors
such as number of examples for training, number of trees,
number of leaves in each tree, cpu, memory, etc. It may take
more than 24 hours to build a boosting model with hundreds
of trees from hundreds of millions of instances with a sin-
gle core cpu. In a practical case, the training can be done
within a few hours via su?cient concurrency in a multi-core
machine with large amount of memory for holding the whole
training set. In the next section we consider an alternative.
The boosted decision trees can be trained daily or every cou-
ple of days, but the linear classifier can be trained in near
real-time by using some flavor of online learning.

In terms of (6), we explore the following choices:

 The first three schemes set learning rates individually per
feature. The last two use the same rate for all features. All
the tunable parameters are optimized by grid search (optima
detailed in Table 2.)
We lower bound the learning rates by 0.00001 for continuous
learning. We train and test LR models on same data with
the above learning rate schemes. The experiment results are
shown in Figure 3.
From the above result, SGD with per-coordinate learning
rate achieves the best prediction accuracy, with a NE al-
most 5% lower than when using per weight learning rate,

 Figure 3: Experiment result for di↵erent learning
rate schmeas for LR with SGD. The X-axis cor-
responds to di↵erent learning rate scheme. We
draw calibration on the left-hand side primary y-
axis, while the normalized entropy is shown with
the right-hand side secondary y-axis.

which performs worst. This result is in line with the conclu-
sion in [8]. SGD with per-weight square root and constant
learning rate achieves similar and slightly worse NE. The
other two schemes are significant worse than the previous
versions. The global learning rate fails mainly due to the
imbalance of number of training instance on each features.
Since each training instance may consist of di↵erent fea-
tures, some popular features receive much more training in-
stances than others. Under the global learning rate scheme,
the learning rate for the features with fewer instances de-
creases too fast, and prevents convergence to the optimum
weight. Although the per-weight learning rates scheme ad-
dresses this problem, it still fails because it decreases the
learning rate for all features too fast. Training terminates
too early where the model converges to a sub-optimal point.
This explains why this scheme has the worst performance
among all the choices.
It is interesting to note that the BOPR update equation
(3) for the mean is most similar to per-coordinate learning
rate version of SGD for LR. The e↵ective learning rate for
BOPR is specific to each coordinate, and depends on the
posterior variance of the weight associated to each individual
coordinate, as well as the “surprise” of label given what the
model would have predicted [7].
We carry out an experiment to compare the prediction per-
formance of LR trained with per-coordinate SGD and BOPR.
We train both LR and BOPR models on the same training
Ranker'
Online'Joiner' Trainer'
features {x}
clicks {y}
models
{x, y}
ads
Figure 4: Online Learning Data/Model Flows.
data and evaluate the prediction performance on the next
day. The result is shown in Table 3.
Table 3: Per-coordinate online LR versus BOPR
Model Type NE (relative to LR)
LR 100% (reference)
BOPR 99.82%
Perhaps as one would expect, given the qualitative similarity
of the update equations, BOPR and LR trained with SGD
with per-coordinate learning rate have very similar predic-
tion performance in terms of both NE and also calibration
(not shown in the table).
One advantages of LR over BOPR is that the model size
is half, given that there is only a weight associated to each
sparse feature value, rather than a mean and a variance. De-
pending on the implementation, the smaller model size may
lead to better cache locality and thus faster cache lookup. In
terms of computational expense at prediction time, the LR
model only requires one inner product over the feature vec-
tor and the weight vector, while BOPR models needs two
inner products for both variance vector and mean vector
with the feature vector.
One important advantage of BOPR over LR is that being a
Bayesian formulation, it provides a full predictive distribu-
tion over the probability of click. This can be used to com-
pute percentiles of the predictive distribution, which can be
used for explore/exploit learning schemes [3].

4. ONLINE DATA JOINER

The previous section established that fresher training data
results in increased prediction accuracy. It also presented a
simple model architecture where the linear classifier layer is
trained online.
This section introduces an experimental system that gener-
ates real-time training data used to train the linear classi-
fier via online learning. We will refer to this system as the
“online joiner” since the critical operation it does is to join
labels (click/no-click) to training inputs (ad impressions) in
an online manner. Similar infrastructure is used for stream
learning for example in the Google Advertising System [1].
The online joiner outputs a real-time training data stream
to an infrastructure called Scribe [10]. While the positive
labels (clicks) are well defined, there is no such thing as a
“no click” button the user can press. For this reason, an
impression is considered to have a negative no click label if
the user did not click the ad after a fixed, and su?ciently
long period of time after seeing the ad. The length of the
waiting time window needs to be tuned carefully.
Using too long a waiting window delays the real-time train-
ing data and increases the memory allocated to bu↵ering
impressions while waiting for the click signal. A too short
time window causes some of the clicks to be lost, since the
corresponding impression may have been flushed out and la-
beled as non-clicked. This negatively a↵ects“click coverage,”
the fraction of all clicks successfully joined to impressions.
As a result, the online joiner system must strike a balance
between recency and click coverage.
Not having full click coverage means that the real-time train-
ing set will be biased: the empirical CTR that is somewhat
lower than the ground truth. This is because a fraction
of the impressions labeled non-clicked would have been la-
beled as clicked if the waiting time had been long enough.
In practice however, we found that it is easy to reduce this
bias to decimal points of a percentage with waiting window
sizes that result in manageable memory requirements. In
addition, this small bias can be measured and corrected for.
More study on the window size and e?ciency can be found
at [6]. The online joiner is designed to perform a distributed
stream-to-stream join on ad impressions and ad clicks uti-
lizing a request ID as the primary component of the join
predicate. A request ID is generated every time a user per-
forms an action on Facebook that triggers a refresh of the
content they are exposed to. A schematic data and model
flow for the online joiner consequent online learning is shown
in Figure 4. The initial data stream is generated when a user
visits Facebook and a request is made to the ranker for can-
didate ads. The ads are passed back to the user’s device
and in parallel each ad and the associated features used in
ranking that impression are added to the impression stream.
If the user chooses to click the ad, that click will be added
to the click stream. To achieve the stream-to-stream join
the system utilizes a HashQueue consisting of a First-In-
First-Out queue as a bu↵er window and a hash map for fast
random access to label impressions. A HashQueue typically
has three kinds of operations on key-value pairs: enqueue,
dequeue and lookup. For example, to enqueue an item, we
add the item to the front of a queue and create a key in the
hash map with value pointing to the item of the queue.
Only after the full join window has expired will the labelled
impression be emitted to the training stream. If no click was
joined, it will be emitted as a negatively labeled example.
In this experimental setup the trainer learns continuously
from the training stream and publishes new models period-
ically to the Ranker. This ultimately forms a tight closed
loop for the machine learning models where changes in fea-
ture distribution or model performance can be captured,
learned on, and rectified in short succession.
One important consideration when experimenting with a
real-time training data generating system is the need to
build protection mechanisms against anomalies that could
corrupt the online learning system. Let us give a simple
example. If the click stream becomes stale because of some
data infrastructure issue, the online joiner will produce train-
ing data that has a very small or even zero empirical CTR.
As a consequence of this the real-time trainer will begin to
incorrectly predict very low, or close to zero probabilities of
click. The expected value of an ad will naturally depend on
the estimated probability of click, and one consequence of
incorrectly predicting very low CTR is that the system may
show a reduced number of ad impressions. Anomaly detec-
tion mechanisms can help here. For example, one can auto-
matically disconnect the online trainer from the online joiner
if the real-time training data distribution changes abruptly.

5. CONTAININGMEMORYANDLATENCY
5.1 Number of boosting trees

 The more trees in the model the longer the time required to
make a prediction. In this part, we study the e↵ect of the
number of boosted trees on estimation accuracy.
We vary the number of trees from 1 to 2,000 and train the
models on one full day of data, and test the prediction per-
formance on the next day. We constrain that no more than
12 leaves in each tree. Similar to previous experiments,
we use normalized entropy as an evaluation metric. The
experimental results are shown in Figure 5. Normalized

en-tropy decreases as we increase the number of boosted trees.
However, the gain from adding trees yields diminishing re-
turn. Almost all NE improvement comes from the first 500
trees. The last 1,000 trees decrease NE by less than 0.1%.
Moreover, we see that the normalized entropy for submodel
2 begins to regress after 1,000 trees. The reason for this phe-
nomenon is overfitting. Since the training data for submodel
2 is 4x smaller than that in submodel 0 and 1.

5.2 Boosting feature importance

Feature count is another model characteristic that can influ-
ence trade-o↵s between estimation accuracy and computa-
tion performance. To better understand the e↵ect of feature
count we first apply a feature importance to each feature.
In order to measure the importance of a feature we use the
statistic Boosting Feature Importance, which aims to cap-
ture the cumulative loss reduction attributable to a feature.
In each tree node construction, a best feature is selected and
split to maximize the squared error reduction. Since a fea-
ture can be used in multiple trees, the (Boosting Feature
Importance) for each feature is determined by summing the
total reduction for a specific feature across all trees.
Typically, a small number of features contributes the major-
ity of explanatory power while the remaining features have
only a marginal contribution. We see this same pattern
when plotting the number of features versus their cumu-
lative feature importance in Figure 6.

 Figure 7: Results for Boosting model with top fea-
tures. We draw calibration on the left-hand side pri-
mary y-axis, while the normalized entropy is shown
with the right-hand side secondary y-axis.

In this part, we study how the performance of the system
depends on the two types of features. Firstly we check the
relative importance of the two types of features. We do so by
sorting all features by importance, then calculate the per-
centage of historical features in first k-important features.
The result is shown in Figure 8. From the result, we can see

that historical features provide considerably more explana-
tory power than contextual features. The top 10 features or-
dered by importance are all historical features. Among the
top 20 features, there are only 2 contextual features despite
historical feature occupying roughly 75% of the features in
this dataset. To better understand the comparative value of
the features from each type in aggregate we train two Boost-
ing models with only contextual features and only historical
features, then compare the two models with the complete
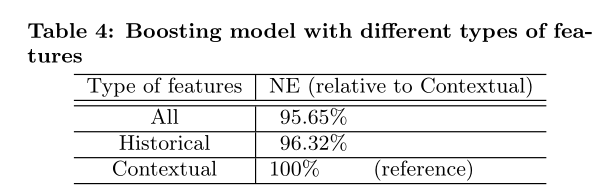
model with all features. The result is shown in Table 4.

 From the table, we can again verify that in aggregate his-
torical features play a larger role than contextual features.

Without only contextual features, we measure 4.5% loss in
prediction accuracy. On the contrary, without contextual
features, we su↵er less than 1% loss in prediction accuracy.
It should be noticed that contextual features are very im-
portant to handle the cold start problem. For new users and
ads, contextual features are indispensable for a reasonable
click through rate prediction.
In next step, we evaluate the trained models with only his-
torical features or contextual features on the consecutive
weeks to test the feature dependency on data freshness. The
result is shown in Figure 9.

 

 From the figure, we can see that the model with contextual
features relies more heavily on data freshness than historical
features. It is in line with our intuition, since historical fea-
tures describe long-time accumulated user behaviour, which
is much more stable than contextual features.
6. COPINGWITHMASSIVETRAININGDATA

A full day of Facebook ads impression data can contain a
huge amount of instances. Note that we are not able to
reveal the actual number as it is confidential. But a small
fraction of a day’s worth of data can have many hundreds of
millions of instances. A common technique used to control
the cost of training is reducing the volume of training data.
In this section we evaluate two techniques for down sampling
data, uniform subsampling and negative down sampling. In
each case we train a set of boosted tree models with 600 trees
and evaluate these using both calibration and normalized
entropy.

6.1 Uniform subsampling

Uniform subsampling of training rows is a tempting ap-
proach for reducing data volume because it is both easy
to implement and the resulting model can be used with-
out modification on both the subsampled training data and
non-subsampled test data. In this part, we evaluate a set
of roughly exponentially increasing subsampling rates. For
each rate we train a boosted tree model sampled at that
rate from the base dataset. We vary the subsampling rate
in {0.001,0.01,0.1,0.5,1}.
The result for data volume is shown in Figure 10. It is in

 Figure 10: Experiment result for data volume. The
X-axis corresponds to number of training instances.
We draw calibration on the left-hand side primary
y-axis, while the normalized entropy is shown with
the right-hand side secondary y-axis.

line with our intuition that more data leads to better per-
formance. Moreover, the data volume demonstrates dimin-
ishing return in terms of prediction accuracy. By using only
10% of the data, the normalized entropy is only a 1% reduc-
tion in performance relative to the entire training data set.
The calibration at this sampling rate shows no performance
reduction.

6.2 Negative down sampling

Class imbalance has been studied by many researchers and
has been shown to have significant impact on the perfor-
mance of the learned model. In this part, we investigate the
use of negative down sampling to solve the class imbalance
problem. We empirically experiment with di↵erent negative
down sampling rate to test the prediction accuracy of the
learned model. We vary the rate in {0.1,0.01,0.001,0.0001}.
The experiment result is shown in Figure 11.
From the result, we can see that the negative down sam-
pling rate has significant e↵ect on the performance of the
trained model. The best performance is achieved with neg-
ative down sampling rate set to 0.025.

6.3 Model Re-Calibration

Negative downsampling can speed up training and improve
model performance. Note that, if a model is trained in a data
Figure 11: Experiment result for negative down
sampling. The X-axis corresponds to di↵erent nega-
tive down sampling rate. We draw calibration on the
left-hand side primary y-axis, while the normalized
entropy is shown with the right-hand side secondary
y-axis.

set with negative downsampling, it also calibrates the pre-
diction in the downsampling space. For example, if the aver-
age CTR before sampling is 0.1% and we do a 0.01 negative
downsampling, the empirical CTR will become roughly 10%.
We need to re-calibrate the model for live tra?c experiment
and get back to the 0.1% prediction with q = p/(p+(1-p)/w)
where p is the prediction in downsampling space and w the
negative downsampling rate.

7. DISCUSSION

We have presented some practical lessons from experiment-
ing with Facebook ads data. This has inspired a promising
hybrid model architecture for click prediction.
• Data freshness matters. It is worth retraining at least
daily. In this paper we have gone further and discussed
various online learning schemes. We also presented
infrastructure that allows generating real-time training
data.
• Transforming real-valued input features with boosted
decision trees significantly increases the prediction ac-
curacy of probabilistic linear classifiers. This motivates
a hybrid model architecture that concatenates boosted
decision trees and a sparse linear classifier.
• Best online learning method: LR with per-coordinate
learning rate, which ends up being comparable in per-
formance with BOPR, and performs better than all
other LR SGD schemes under study. (Table 4, Fig 12)
We have described tricks to keep memory and latency con-
tained in massive scale machine learning applications
• We have presented the tradeo↵ between the number of
boosted decision trees and accuracy. It is advantageous
to keep the number of trees small to keep computation
and memory contained.
• Boosted decision trees give a convenient way of doing
feature selection by means of feature importance. One
can aggressively reduce the number of active features
whilst only moderately hurting prediction accuracy.
• We have analyzed the e↵ect of using historical fea-
tures in combination with context features. For ads
and users with history, these features provide superior
predictive performance than context features.
Finally, we have discussed ways of subsampling the training
data, both uniformly but also more interestingly in a biased
way where only the negative examples are subsampled.

8. REFERENCES

[1] R. Ananthanarayanan, V. Basker, S. Das, A. Gupta,
H. Jiang, T. Qiu, A. Reznichenko, D. Ryabkov,
M. Singh, and S. Venkataraman. Photon:
Fault-tolerant and scalable joining of continuous data
streams. In SIGMOD, 2013.
[2] L. Bottou. Online algorithms and stochastic
approximations. In D. Saad, editor, Online Learning
and Neural Networks. Cambridge University Press,
Cambridge, UK, 1998. revised, oct 2012.
[3] O. Chapelle and L. Li. An empirical evaluation of
thompson sampling. In Advances in Neural
Information Processing Systems, volume 24, 2012.
[4] B. Edelman, M. Ostrovsky, and M. Schwarz. Internet
advertising and the generalized second price auction:
Selling billions of dollars worth of keywords. In
American Economic Review, volume 97, pages
242–259, 2007.
[5] J. H. Friedman. Greedy function approximation: A
gradient boosting machine. Annals of Statistics,
29:1189–1232, 1999.
[6] L. Golab and M. T. ¨ Ozsu. Processing sliding window
multi-joins in continuous queries over data streams. In
VLDB, pages 500–511, 2003.
[7] T. Graepel, J. Qui˜ nonero Candela, T. Borchert, and
R. Herbrich. Web-scale bayesian click-through rate
prediction for sponsored search advertising in
Microsoft’s Bing search engine. In ICML, pages 13–20,
2010.
[8] H. B. McMahan, G. Holt, D. Sculley, M. Young,
D. Ebner, J. Grady, L. Nie, T. Phillips, E. Davydov,
D. Golovin, S. Chikkerur, D. Liu, M. Wattenberg,
A. M. Hrafnkelsson, T. Boulos, and J. Kubica. Ad
click prediction: a view from the trenches. In KDD,
2013.
[9] M. Richardson, E. Dominowska, and R. Ragno.
Predicting clicks: Estimating the click-through rate
for new ads. In WWW, pages 521–530, 2007.
[10] A. Thusoo, S. Antony, N. Jain, R. Murthy, Z. Shao,
D. Borthakur, J. Sarma, and H. Liu. Data
warehousing and analytics infrastructure at facebook.
In SIGMOD, pages 1013–1020, 2010.
[11] H. R. Varian. Position auctions. In International
Journal of Industrial Organization, volume 25, pages
1163–1178, 2007.
[12] J. Yi, Y. Chen, J. Li, S. Sett, and T. W. Yan.
Predictive model performance: O✏ine and online
evaluations. In KDD, pages 1294–1302, 2013.

https://zhuanlan.zhihu.com/p/34770123

https://zhuanlan.zhihu.com/p/20596989

https://t.cj.sina.com.cn/articles/view/5901272611/15fbe462301900lf9i

https://blog.csdn.net/lilyth_lilyth/article/details/48032119