Learning C++ No.27 【布隆过滤器实战】

引言

北京时间：2023/5/31/22:02，昨天的计算机导论考试，三个字，哈哈哈，摆烂，大致题目都是一些基础知识，但是这些基础知识都是非常非常理论的知识，理论的我一点不会，像什么操作系统的分类，什么IP地址的计算，什么网络协议，反正是什么都不会，而且还有什么填空题，像什么秘钥什么什么鬼的，具体我不太记得清了，反正听都没听说过，哈哈哈！最烦人的题目还属是IP地址，计算什么子网个数，什么什么地址，反正一点不会，要不是有考一些进制转换和有关硬件方面的知识，可能连50分都考不到，总体来说，在我东扯西扯的情况下，应该勉勉强强有个60分吧！谁让我就算是考前最后一分钟都没打算复习一点，何谈整个学期都没听过这个课，真的抽象，莫名不以为耻，反以为荣，哈哈哈，无所谓啦！不重要，重要的是该篇博客要学习的新知识，有关布隆过滤器和哈希切分的知识！go，go，go

什么是布隆过滤器

现在写博客的状态，没有之前那么好，不然现在肯定得给你们来一个长篇大论，再而引出话题，哈哈哈！同理，和之前一样，认识一个新事物最快的方法就是通过图示，所以当我们开始想要去了解布隆过滤器时，如下图所示：

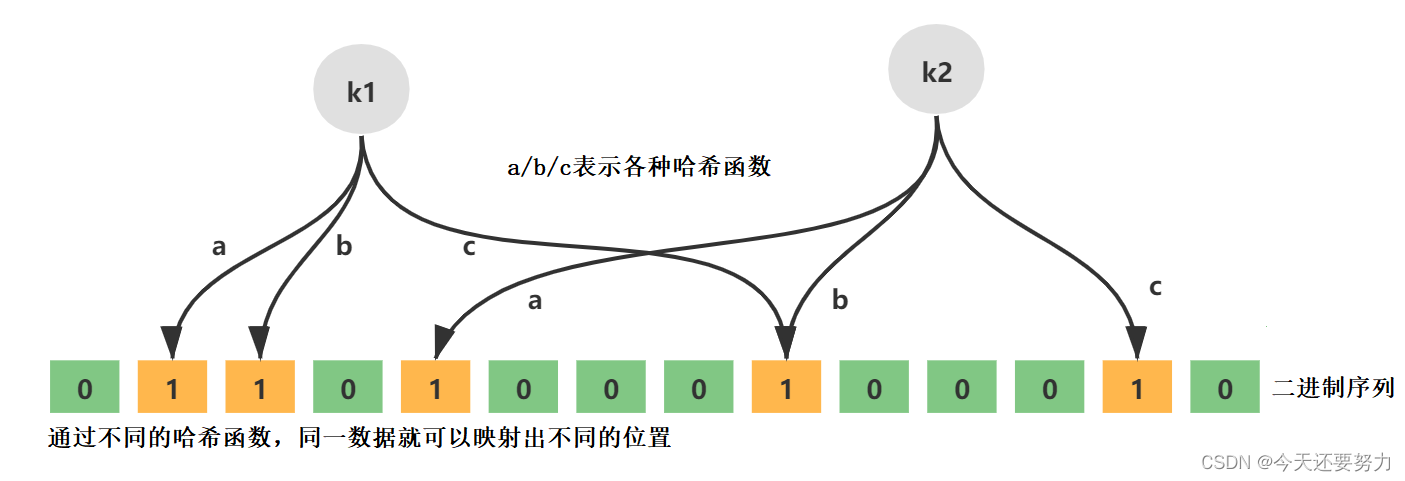
注意：此时该结构叫布隆过滤器，不再是位图结构，虽然布隆过滤器本质上就是位图结构和哈希表的一个结合

如上图所示，搞懂布隆过滤器最大的问题不是搞懂上图表示的含义，而是搞懂，为什么需要按照上图的方式来设计，也就是应了古人所说的，对一个新知识，我们不仅要知其然，更要知其所以然，充分表明，咱的博客绝对不是水文，不像是有的文章，一上来就是布隆过滤器的概念，由谁谁谁几几年提出，有什么优点，什么用途之类的，哈哈哈，还得是咱，直接跟你聊所以然，哈哈哈，如下：就是为什么我们要设计出该结构，而不是继续使用位图结构或者哈希表来映射数据

首先解决上述两个问题，为什么不直接使用哈希表或位图结构解决上述对应数据存储的问题，为什么不使用哈希表，这里我就不多说了，简简单单，在学习位图结构的时候，我们就已经知道了，当然这也就是我们为什么需要学习位图结构的原因，因为使用哈希表（开散列）去存储数据的话，那么一个结点不仅有对应的数据，还要有对应的指针，这样就会导致一个结点所占的字节数很大，也就是使用哈希表存储一个数据需要使用的内存很大，所以当我们需要存储大量的数据（几十亿），那么此时使用哈希表就不再合适，所以当我们要存储几十亿个数据时，第一时间需要考虑使用的就是位图结构或者布隆过滤器，那么具体什么时候使用位图结构，什么时候使用布隆过滤器呢？如下：

本质原因是被储存数据类型原因，在之前学习位图结构时，我们默认存储的类型是整形，当时并没有考虑别的类型，经典的就是字符串类型，此时当我们考虑到字符串类型时，就会发现，位图结构的缺点，一般只能映射整形，为什么只能映射整形呢？本质还是为了减少冲突，也就是（重点）：如果你是整形，那么无论是数据个数还是数据长度，都是固定的，一个整形数据根据对应的映射函数就只能计算出一个比特位位置，除非你是神仙，否则你永远不可能让两个不同的整形数据映射到同一个比特位上，可是，如果此时数据不是整形，而是字符串类型，那么就非常的不友好，特别是中文情况下，先看英文，如果是一个英文字符串，假如字符串长度为n，那么很容易就可以知道，此时该字符串有26^n种可能，多的不说，少的不唠，如果n为6，那么就有3亿多种组合，如果为7，那么就是神仙都算不明白（大概5万多亿），何谈中文，虽然无论是英文还是中文，日常常用的组合是在一定范围内的，但是这种情况是存在的，那么我们就需要解决

可能上述讲了这么多，你们都还没有发现问题是什么，本质问题其实上述已经很清晰了，就是整形由于固定，所以在根据映射函数映射对应比特位时，不可能存在两个不同的整形，映射到同一个位置，但是由于字符串类型（英/中）拥有的组合类型极大（本质是由于字符串本身的不确定性和长度不固定性所导致），所以此时两个不同的数据出现映射到同一个比特位的概率就会非常大，类似于哈希冲突，但又不是哈希冲突，哈希冲突是两个相似却不相同的数据映射到了同一位置，而此时的位冲突是两个不同的数据，由于根据映射函数计算出的哈希值相同，导致映射在了二进制序列某一个唯一的位上，此时该位置不像是哈希表中的位置一样，可以使用指针将数据链接起来，而是直接实打实的就是冲突了，也就是这个比特位代表的就不再是某一个特定的数据，而是两个或者很多个数据，并且具体是什么数据，这个是不可控的，导致我们完全懵逼，所以对应这种场景，我们就需要解决，如下：

简简单单，成功引出话题，为什么设计出上图所示结构（布隆过滤器），本质还是那个道理，减少冲突，提高发生冲突时，解决冲突的效率，也就是如上图所示结构，一个数据使用不同哈希函数映射多个位置，不再是像位图结构，一个数据只映射一个位置，这也就是位图结构和布隆过滤器最大的区别，可能这样说，大家还存在一定的疑问，就是为什么一个数据映射了多个位置后，数据直接冲突的概率就会降低呢？因为我们要明白，一个数据无论是存在位图结构中，还是布隆过滤器中，只有当它对应通过哈希函数映射的比特位被置成1，才表示该数据是存在的，如果是位图结构只映射一个比特位，那么这个比特位被其它数据映射的可能性就很大，但是如果一个数据同时映射多个位置，只有当对应通过不同哈希函数映射的比特位同时被置成1，那么此时才能表示该数据存在，哪怕是其中有一个或者两个比特位被其它冲突数据置成了1，只要不是对应全部比特位被置成1，那么此时程序也还是合理的，不存在冲突问题，所以综上所述：同时映射多个位置的方法，可以大大的降低数据冲突的概率，如下图所示：

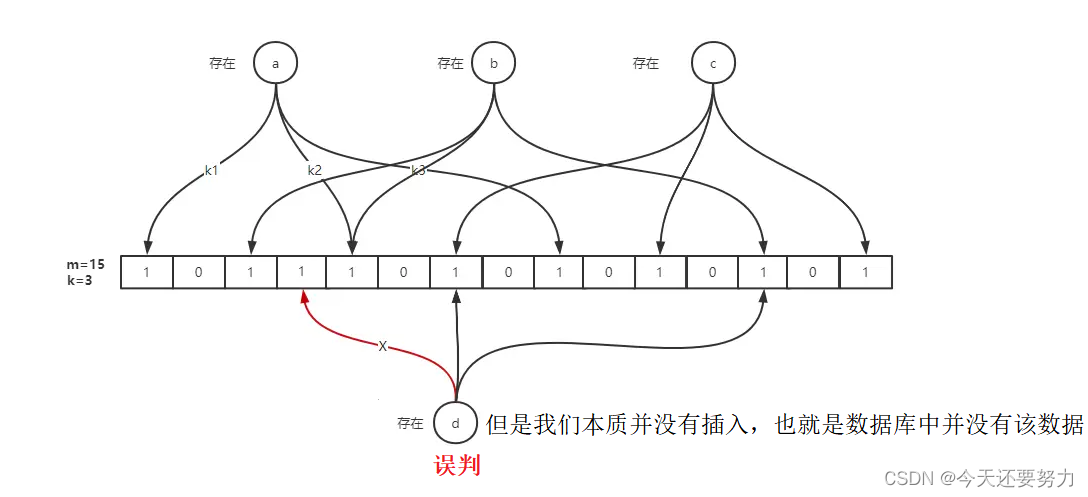
再次强调： 所以只有当该数据存在的情况，此时才有可能存在误判，并且此时存在两种可能，一种是该数据确实在布隆过滤器中，另一种是该数据不在布隆过滤器中，但由于别的数据和该数据哈希值发生冲突，导致在映射比特位的时候，将该数据对应的全部比特位置成了1，从而导致误判，也就是不存在变成了存在，当然，在我们的布隆过滤器面前，误判的概率相对于位图结构，可以说降低了非常多，所以这种误判此时我们是接受的，并且是合理的，当然，如果遇到这种情况，此时最好的解决方法就是进行二次验证，通过向数据库中查询，判断该数据是否真正存在

总：一个数据在二进制序列上映射的位越多，那么冲突的概率就越低，但，这样会导致需要的二进制序列越长，也就是使用的空间越多

所以如何控制一个数据在二进制序列上映射的位，当然也就是哈希函数的个数，从而实现空间节约的情况下让误判率最低呢？如下图所示：

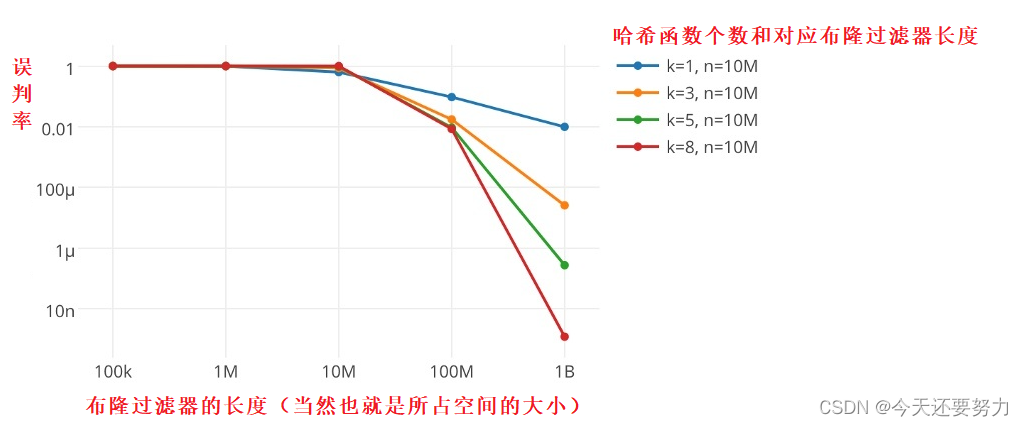
通过上图，此时我们可以发现，在一定的数据范围内，哈希函数的个数和布隆过滤器的长度（空间的大小）之间存在一定的关系，可以让误判率达到最低，如下公式所示：

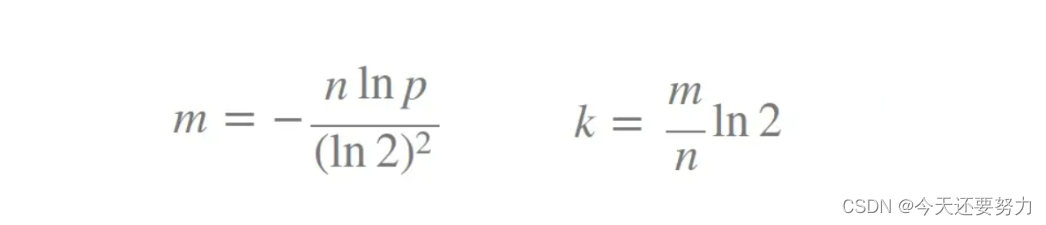
其中n表示插入元素个数 m表示布隆过滤器的长度 k表示哈希函数的个数 p为误判率

所以此时如果我们使用三个布隆过滤器，那么，可以得到一个数据个数和布隆过滤器长度之间的关系，4.3n = m，也就是表示当我们想要让一个数据可以使用哈希哈数映射三个比特位，并且让误判率达到最低，耗费的空间达到最小，那么此时布隆过滤器的长度就需要是数据个数的4.3倍，也就是4.3n个比特位，只要这样，才可以将布隆过滤器的性能给拉满，将效率提升到最高

布隆过滤器简易代码实现

搞定了上述有关哈希函数个数和布隆过滤器长度之间的关系，那么我们就可以正式通过代码来实现一下布隆过滤器啦！当然同理上述所说，此时我们使用的是3个哈希函数，具体哈希函数如下：

上述就是三个哈希函数，实现的目的就是为了减少哈希冲突（当然前提，通过映射将对应哈希值转换成整形），具体实现原理是通过一定的数学公式得出，感兴趣的同学可以参考下述链接：哈希函数详解

其次搞定了有关哈希函数的知识，此时就是布隆过滤器长度的问题，由于我们同理上述所说，使用的是3个哈希函数，所以此时布隆过滤器和插入元素的个数之间的关系是4.3n = m，也就是需要开辟的空间大小是4.3倍的比特位，所以代码如下所示：

当然由于布隆过滤器本质上还是一个位图结构，只不过此时利用了哈希表的特性，所以我们是通过封装 bitmap 实现，具体代码如下所示：本质上代码实现和上述的原理是一致的，就是让一个数据通过不同的哈希函数去映射多个位置而已，如下代码所示：

同理检查一个数据是否存在布隆过滤器中，如下代码所示：

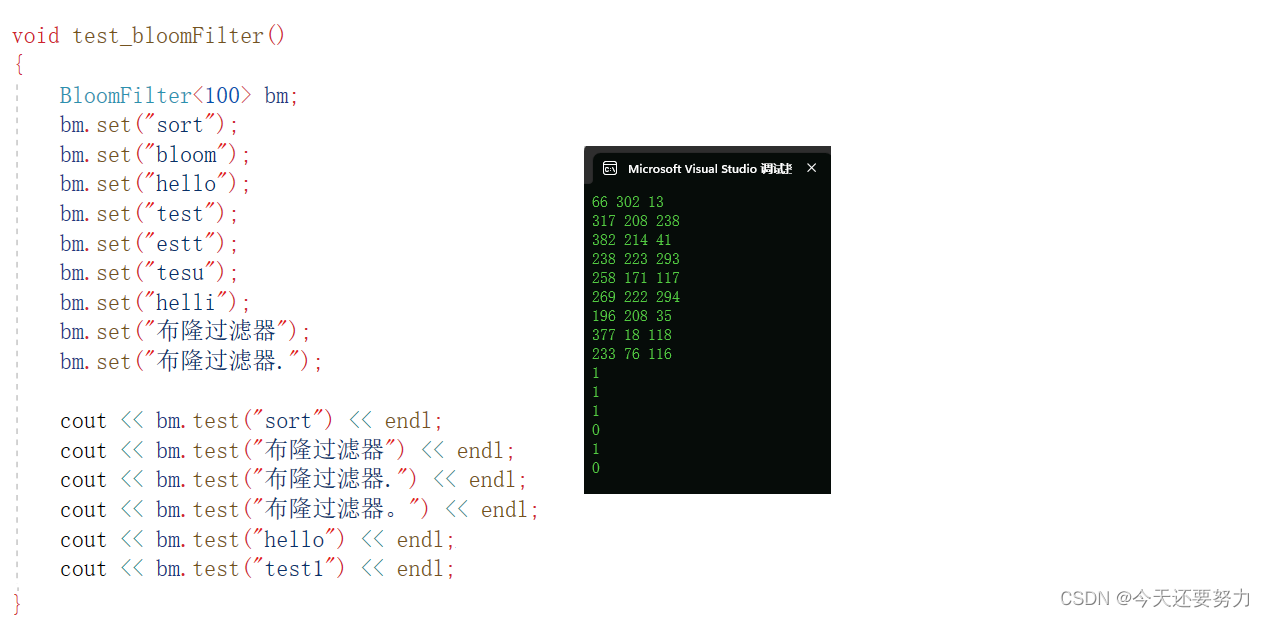
测试代码如下：

布隆过滤器使用场景

搞定了上述布隆过滤器简易代码实现的问题，布隆过滤器的基本知识我们就学习完啦！接下来就是讲讲在实际生活中，那些场景下需要使用到布隆过滤器，并且使用布隆过滤器可以解决那些实际问题，如下：

布隆过滤器基本使用场景：
利用布隆过滤器减少磁盘 IO 或者网络请求，因为一旦一个值必定不存在的话，我们可以不用进行后续昂贵的查询请求，或者是将布隆过滤器结合数据库索引使用，可以加速向数据库的查询操作，提升查询效率，或者是那些能容忍误判的场景，例如：判断一个昵称是否使用过，因为只有当误判的时候才需要去访问数据库，如果根本就不存在，那么就可以直接使用，不需要进行后序操作，当然也就是不需要频繁访问数据库，这样效率就大大提高（因为数据库中的数据本质是存储在磁盘或者固态硬盘中）

布隆过滤器解决实际问题：
给定两个文件，分别有100亿个query（字符串数据），我们只有1G内存，如何找到两个文件的交集？
同理之前学习位图结构时，解决海量数据问题的思路，只不过此时不是整形，而是字符串类型而已，原理：先把其中一个文件中的所有数据映射进布隆过滤器，然后遍历另一个文件（调用test）判断是否是交集，也就是判断该文件数据对应哈希值在二进制序列上映射的位，在布隆过滤器中是否已经存在，如果存在，此时该数据就是交集，反之不是，同理，许多类似的海量数据处理问题都一样，这里不一一讲解，反正布隆过滤器在数据映射和判断是否重复方面（前提非整形），都有着得天独厚的优势

什么是哈希切分

但是使用布隆过滤器处理上述问题，该方法的效率非常的低，具体原因就是遍历效率很低，所以此时我们使用下述方法：当然也就是我们将要重点讲解的哈希切分的方法，这样可以高效率的解决上述两个文件找交集的问题，本质从名字（哈希切分）就可以看出，是一个和哈希映射有关的方法，具体如下：

具体原理：将其中一个文件（A）通过哈希函数分成若干个小文件，如：i = hashfunc(query)%1000 ，此时我们就将其中一个文件给切分成了1000个小文件，同理，另一个文件（B）也切分成若干个小文件，然后两个文件寻找交集数据的时候，只要让A文件中的某一个小文件去和B文件中对应的小文件匹配就行，具体如下图所示：

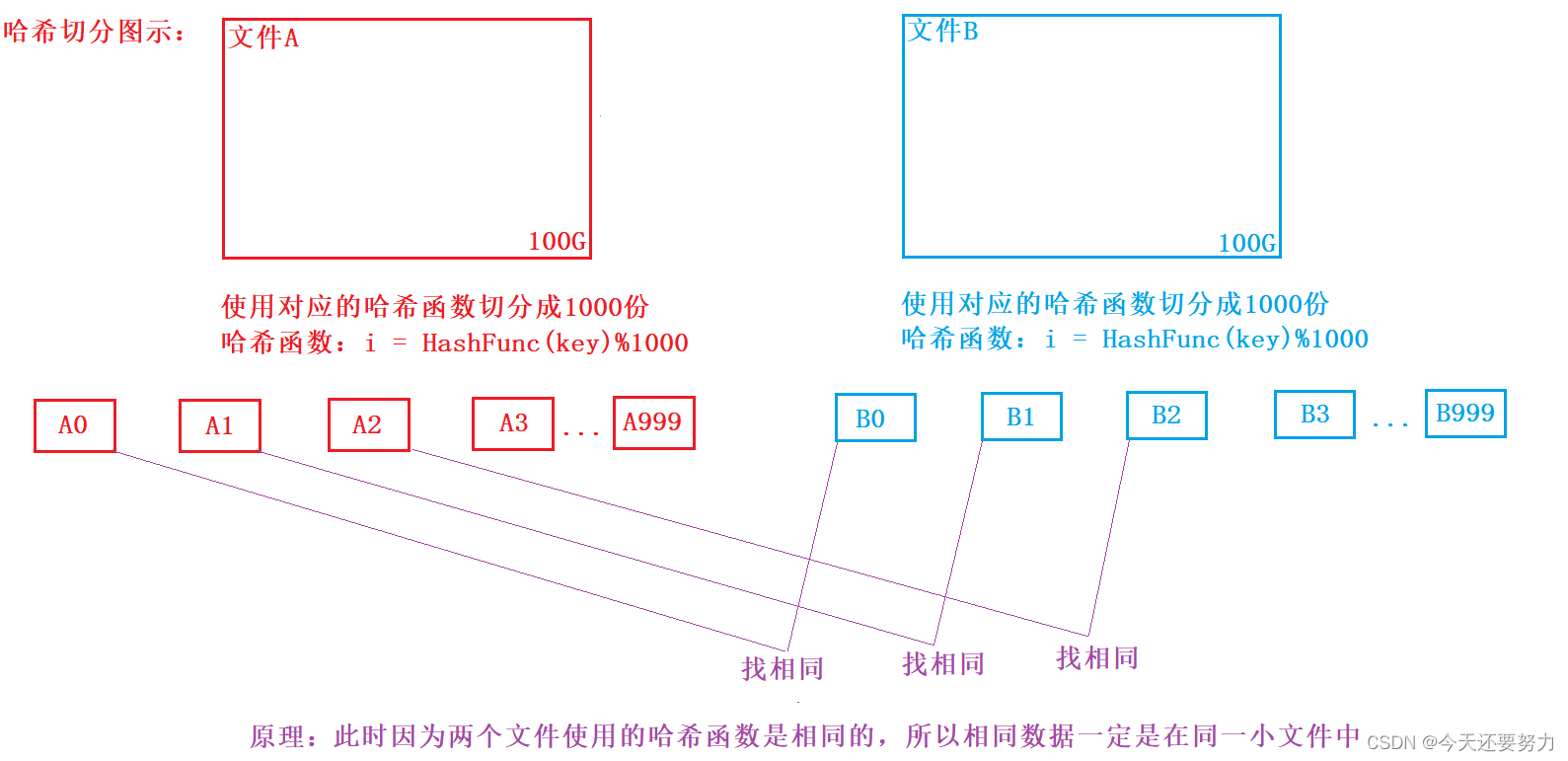
如上图所示，此时就是让两个文件中的数据，根据对应同一个哈希函数，算出对应的哈希地址（i），然后将数据对应数据存储在该哈希地址对应的小文件中（具体可以使用vector存储），然后让对应哈希地址的小文件进行数据匹配就行，例如上图所示的A0和B0相匹配，A1和B1相匹配，具体原理：同理上图，因为两个文件使用的哈希函数是相同的，所以只要是相同的数据，就一定在同类型哈希地址对应的小文件中，进而就可以找到交集，并且明白：由于我们已经进行了哈希切分，大文件变成了小文件，那么此时所需要的内存就变小了，那么最终比较的时候，就可以直接放到内存中去比较，而不需要通过位图的方式去比较，从而使得效率大大提高，但，此时使用该方法（哈希切分）会面临一个问题，如下：

也就是当文件A或者文件B当中有大量的重复数据时，这样就会导致某一个小文件中的数据量非常多，那么导致该小文件的大小超过内存大小，导致无法存储在内存，最终无法进行数据匹配，找到交集，具体解决方法如下： 在进行哈希切分时，一定要记录每一个小文件的大小，如果该小文件太大，此时就进行区分，看该小文件中的数据是大量的重复数据，还是大量的非重复数据，如果是大量的非重复数据，那么就进行二次切分，如果是大量的重复数据，那么就需要进行去重处理，区分方法： 使用一个unordered_set，依次读取小文件，插入unordered_set中，如果整个小文件都可以成功插入（return false在这里不表示失败），那么此时表示的就是该小文件中都是重复数据，如果不可以成功插入(数据太大，内存不够)，那么就表示该小文件中都是非重复数据，此时就去重，因为：如果是大量重复，那么此时在unordered_set中会直接去重，所以就可以插入成功，如果是大量不重复，那么就会导致插入数据时，内存不够，导致插入unordered_set失败

扩展

如何让布隆过滤器使支持删除元素的操作：
将对应的比特位改成引用计数，此时对应的比特位就不是一个比特位，而是一个计数器，同理，0就是没有映射，1就是一个数据映射该位置，2就是两个数据映射该位置，3就是三个数据映射该位置，通常的布隆过滤器只使用一个比特位来表示元素是否存在于集合中，它通过哈希函数将元素映射到多特位上，并将这些比特位的值都设置为1。在查询操作中，如果对应位置的比特位都为1，则该元素可能存在于集合中；否则，该元素一定不存在于集合中。因此，标准布隆过滤器可以高效地检测某个元素是否属于集合，但不支持删除元素操作，计数型布隆过滤器在比特位的基础上，对每个位置使用一个计数器来记录元素出现的次数。当需要添加某个元素时，各个哈希函数计算出的哈希值所对应的位置上的计数值都会加1；当需要删除某个元素时，对应位置上的计数值都会减1。在检查某个元素是否存在时，需要检查各个哈希函数计算出的哈希值所对应的位置上的计数值是否都大于等于1，并且明白，此时的计数器可以是一个数组，也叫计数器数组，同理，此时计算出了对应数据的哈希值之后，不是在对应的比特位上置1，而是在对应的数组下标中进行++操作，如果该位置被映射一次，那么就是1，被映射两次，那么就++两次，也就是2，所以明白，计数器类型的布隆过滤器使用的是数组形式，内存需求就会非常高，类似于计数排序的实现思路

总结：最近的学习效率较低，不知道为什么，反正没有以前的干劲了，但是不怕，充分反省和利用好时间，减少摆烂就行，加油啦！

布隆过滤器简易代码如下：

template<size_t N, class K = string, class Hash1 = BKDRHash, class Hash2 = APHash, class Hash3 = DJBHash>//给定三个函数模板
class BloomFilter
{
public:
	void set(const K& key)
	{
		size_t len = N * _x;
		size_t hash1 = Hash1()(key) % len;
		_bm.set(hash1);

		size_t hash2 = Hash2()(key) % len;
		_bm.set(hash2);
		size_t hash3 = Hash3()(key) % len;
		_bm.set(hash3);                 
		cout << hash1 << " " << hash2 << " " << hash3 << endl;
	}

	bool test(const K& key)
	{
		size_t len = N * _x;
		size_t hash1 = Hash1()(key) % len;
		if (_bm.test(hash1) == 0)
		{
			return false;//是0表示不在，就返回false
		}

		size_t hash2 = Hash2()(key) % len;
		if (_bm.test(hash2) == 0)
		{
			return false;
		}

		size_t hash3 = Hash3()(key) % len;
		if (_bm.test(hash3) == 0)
		{
			return false;
		}

		return true;
	}
	
private:         
	static const size_t _x = 4;
	bitmap<N*_x> _bm;          
};                             
void test_bloomFilter()        
{
	BloomFilter<100> bm;
	bm.set("sort");
	bm.set("bloom");
	bm.set("hello");
	bm.set("test");
	bm.set("estt");
	bm.set("tesu");
	bm.set("helli");
	bm.set("布隆过滤器");
	bm.set("布隆过滤器.");

	cout << bm.test("sort") << endl;
	cout << bm.test("布隆过滤器") << endl;
	cout << bm.test("布隆过滤器.") << endl;
	cout << bm.test("布隆过滤器。") << endl;
	cout << bm.test("hello") << endl;
	cout << bm.test("test1") << endl;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66