- 1python中print输出浮点数保留几位小数_print('%.2f'%x)
- 2bootstrap dialog对话框,完成操作提示框
- 3细说数字化转型之:为什么要数字化?
- 4Django问题:cannot import name ‘url‘ from ‘django.conf.urls‘解决方法_cannot import name 'url' from 'django.conf.urls
- 5CV笔记——(第八讲)深度学习中的优化策略详解(含dropout与迁移学习讲解)_深度学习 z字型
- 6Python安装教程(2023最新)_pathon 安装指南
- 7阿里云centos7安装Nginx_阿里云安装nginx
- 8Qt Designer 最新中文手册文档(Qt6)_pyqt6 designer 详解
- 9Cloud Computing 云计算基础_云计算基础(云计算基本概念,虚拟化、容器化、分 布式计算、分布式存储等)
- 10RC522(RFID射频模块)读卡ID的简单应用_typea 寻卡 0x52 0x26
机器学习基础-监督学习与无监督学习
赞
踩
机器学习基础-监督学习与无监督学习
机器学习(Machine Learning)主要研究计算机系统对特定任务的性能,逐步进行改善的算法和统计模型。
通过输入海量数据对模型进行训练,使模型掌握数据所蕴含的潜在规律,进而对新输入的数据进行准确的分类和预测。
机器学习主要包括:有监督学习,无监督学习及强化学习,神经网络与深度学习,集成学习。
我们主要介绍和学习的是监督学习和无监督学习。

无监督学习算法采用一组仅包含输入的数据,通过寻找数据内在结构进行样本点的分组或聚类。该算法从没有被分类和测试的数据中去学习,无监督学习不是响应反馈,而是识别数据中的共性特征,对于一个新数据,可以通过判断其中是否存在这种特征,来做出相应的反馈。
无监督学习的核心应用是统计学中的密度估计和聚类分析。

监督学习算法构建了包含输入和所需输出的一组数据的数学模型,这些数据称为训练数据,由一组训练样本组成。
监督学习主要包含分类和回归,当输入为离散值时候,使用分类算法,当输入为连续值时,使用回归算法。
相似度学习是和分类与回归都密切相关的监督机器学习,它的目的是使用相似性函数从样本中进行学习,这个函数可以度量两个样本的相似度或关联度。
监督学习的三要素:模型,策略,算法。

如下图所示:监督学习过程,类似于求解二元一次方程,输入数据进行求解,求解完成,带入新数据进行预测,和房屋售卖情况预测也类似,通过大量数据进行训练,待模型成熟,输入新数据进行预测。

模型评估策略和模型选择
训练集:输入到模型中对模型进行训练的数据集合。
测试集:模型训练完成后测试训练效果的数据集合。
损失函数:用来恒衡量模型预测误差的大小。
定义:选取模型f为决策函数,对于给定的输入参数x,f(x)为预测结果,y为真实值,f(x)与y之间肯会存在偏差,我们使用损失函数来度量预测偏差的程度,记作L(y,f(x))
损失函数是系数的函数,损失函数值越小,误差越小,模型越好。
对于0-1损失函数,只要有偏差,则损失函数为1,当且仅当预测值和真实值相等的时候,损失函数为0.
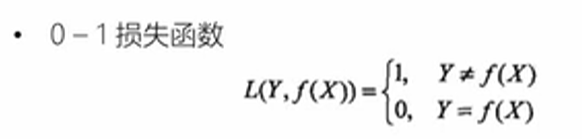
平方损失函数,真实值与预测值之差的平方。
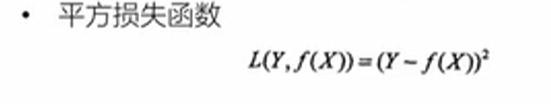
绝对损失函数,真实值与预测值之差的绝对值。
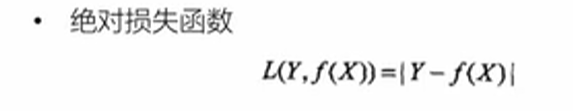
对数损失函数,对条件概率进行取对数。
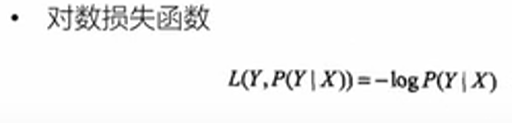
经验风险:模型f(x)关于训练集数据的平均损失函数称为经验风险,公式入戏:
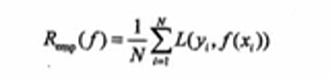
经验风险最小化(ERM),该策略认为经验风险最小的模型就是最优模型,当样本足够大的时候ERM有很好的学习效果,当样本比较小的时候,ERM就会出现一些问题。
训练误差:关于训练集的平均损失,训练误差的大小可以用来判定给定的问题是否容易学习。
测试误差:关于测试集的平均损失,真正的反映了模型对未知事物的预测能力,这种能力称为泛化能力。
过拟合:模型在训练集效果很好,学习的太彻底,以至于把噪声数据也学习到了,到测试集效果比较差,模型的预测能力不足,即泛化能力差。
欠拟合:模型对特征的学习不够,在训练集的表现就很不好。
我们观察如下图,10个样本点,用一个M次数多项式拟合函数进行拟合,当次数M等于0或者1的时候,我们称为欠拟合,当次数M等于3的时候,我们称为合适拟合,当M等于9的时候,我们称为过拟合。

如下图所示,当模型的复杂度越大,训练误差就会逐渐减小,趋近于0,而测试误差会先减小到最小值,然后增大。故模型的复杂度并不是越大越好,当模型的复杂度过大就会发生过拟合。

正则化:在ERM的基础上,为防止过拟合提出来的策略,在经验风险上加上表示模型复杂度的正则化项,也称为惩罚项。
结构风险最小化的典型实现就是正则化,如下图公式所示,第一项是经验风险,第二项是正则化项,正则化项可以去不同的形式。
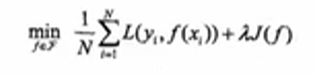
数据集的划分:如果样本充足,一种简单的方法就是将数据集分成三部分,即训练集,验证集和测试集。
训练集用于训练模型,验证集用于模型选择,测试集用于预测评估。
当数据量不足,可以重复利用数据,做交叉验证。
1-简单交叉验证:数据随机的分成两部分,如70%作为训练集,剩下30%作为测试集,训练集训练得到不同模型,测试集进行测试得到最优模型。
2-S折交叉验证:将数据分成S个互不相交,大小相同的数据集,S-1个做训练集,剩下的1个做测试集
监督学习问题主要划分成两类,即分类问题和回归问题。
分类问题预测数据属于哪一类别,即离散问题。
回归问题根据数据预测一个数值,即连续问题。回归问题的学习等价于函数拟合。
例如:对于房屋售卖的预测,通过给定大量数据去训练模型预测房屋能否卖出去,这就是一个典型的分类问题,结果就两种可能,即能卖出去(1)或者卖不出去(0)。
再例如:对房屋的售卖价格进行预测,或者对于卖出的概率进行预测,都是回归问题,因为结果为一个连续的数值,而不是离散的0或者1。
回归问题
回归问题的分类
按照输入变量的个数,分为一元回归和多元回归
按照模型的类型,分为线性回归和非线性回归
回归学习的损失函数选为平方损失函数,回归问题可以用最小二乘法来求解。
梯度下降算法
梯度下降是常用的一阶优化方法,是求解无约束优化最简单,最经典的方法之一。
梯度方法:函数变化增长最快的方向,即变量沿此方向变化时,函数增长最快。
负梯度方向:函数变化减少最快的方向,即变量沿此方向变化时,函数减少最快。
损失函数是系数的函数,如果系数沿着损失函数的负梯度变化,此时损失函数减少最快,能够以最快速度下降到最小值。
如下图所示,沿着负梯度方向迭代,迭代后的参数使得损失函数更小。

梯度下降一般找到是局部最优解,未必是全局最优解。


