- 1安装docker compose_安装docker-compose
- 2【UE4】如何获取/下载虚幻4(Unreal Engine4)源码
- 3利用Pytorch实现ResNet网络
- 4python中使用多进程multiprocessing并获取子进程的返回值_multiprocessing开启另一线程进行实例化对象怎么返回到主线程
- 5Maven 仓库国内镜像源收藏_maven 厂库国内镜像
- 6【批处理脚本】-2.1-测试IP连接命令ping_批处理获取ip是否通
- 7学习笔记8-python skimage图像处理(实例演示-代码讲解)_rough-wall.png墙壁图像处理skimage
- 83D Gaussian Splatting的使用_训练3d gaussian splatting模型步骤
- 9mvn offline 离线安装依赖和生成jar包
- 10windows安装pip工具_qlyd1yvx
Leetcode 968 监控二叉树
赞
踩
理解题意:
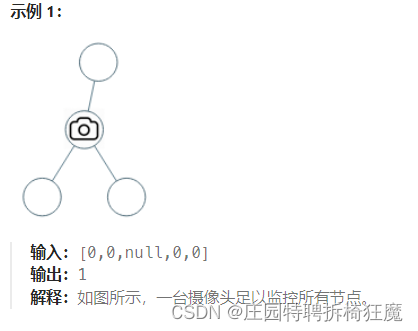
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。什么是监控?
目标:最少的摄像头数目监控所有节点。
解题思路:
采用贪心的思路来解题。首先明确局部最优解和全局最优解。
全局最优解:最少的摄像头监控所有节点
局部最优解:尽可能用中间的节点来监控周围节点,来达到较少摄像头的目的。——即摄像头放在叶子节点,只能覆盖其父节点。而摄像头放根节点,只能覆盖左右孩子,但是中间节点至少可以覆盖:父节点+左右孩子,三个节点。
两端的节点主要是最上面的跟节点和最下面的叶子节点。
根节点只有一个,所以尽可能从叶子节点上节省摄像头。在一条链路上,两个摄像头之间可以间隔两个节点。一个覆盖节点和摄像头间隔一个节点。
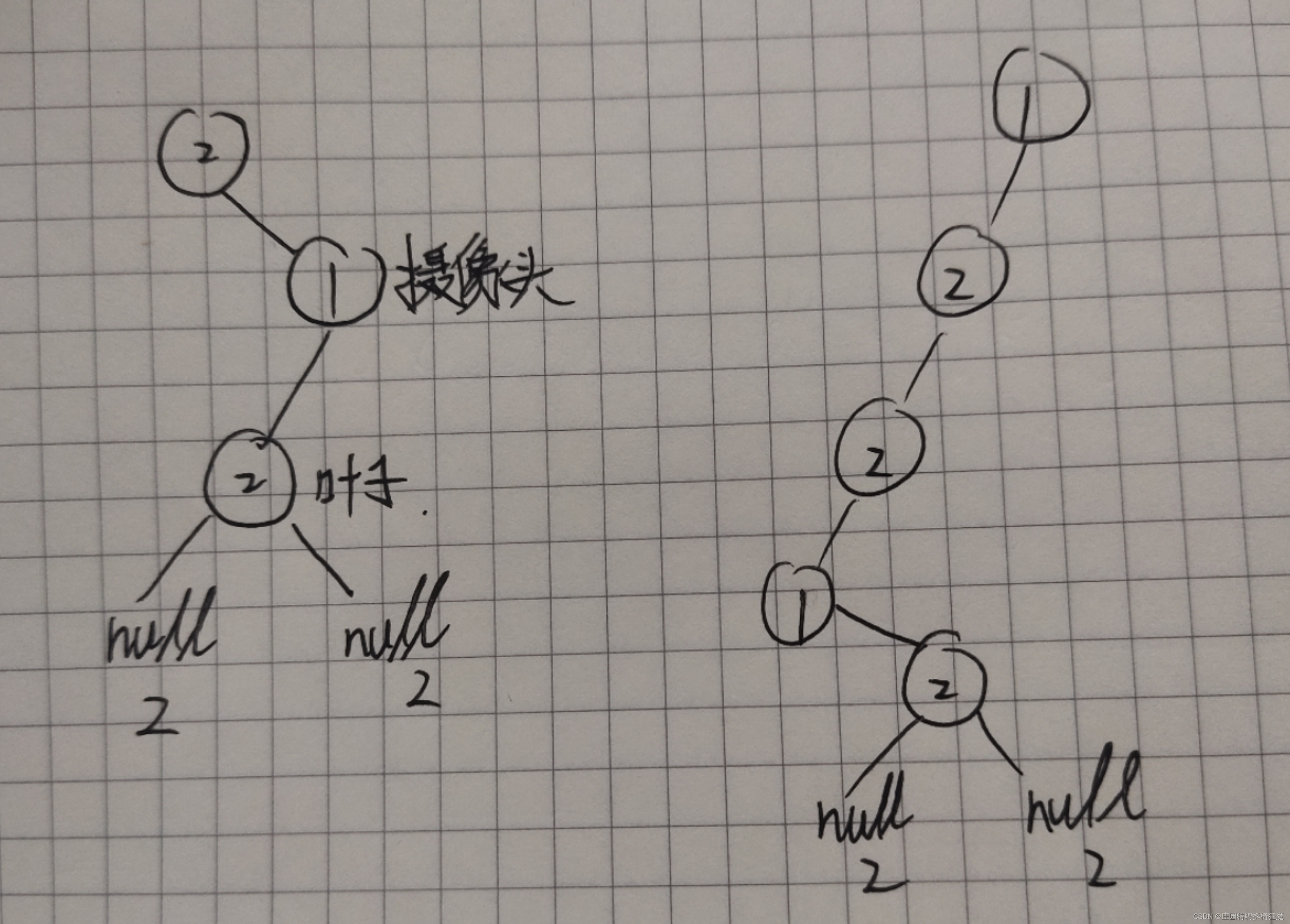
分情况讨论:节点的状态分为:0未覆盖、1摄像头、2已覆盖
注意:null节点的状态应为2.
1.左孩子|右孩子有一个0状态,则父节点一定要设置摄像头(状态1)来保证全覆盖。
2.左右孩子没有0状态,且左右孩子有一个摄像头,则父节点状态一定为覆盖(状态2)
3.左右孩子都是已覆盖状态,则当前节点的父节点一定有一个摄像头(状态1),来保证覆盖当前节点(状态2)的同时覆盖更多的情感。
从叶子节点开始遍历各个节点的状态,并统计摄像头的个数。
其中总是通过左右孩子确定当前节点,则采用后续遍历:左右中
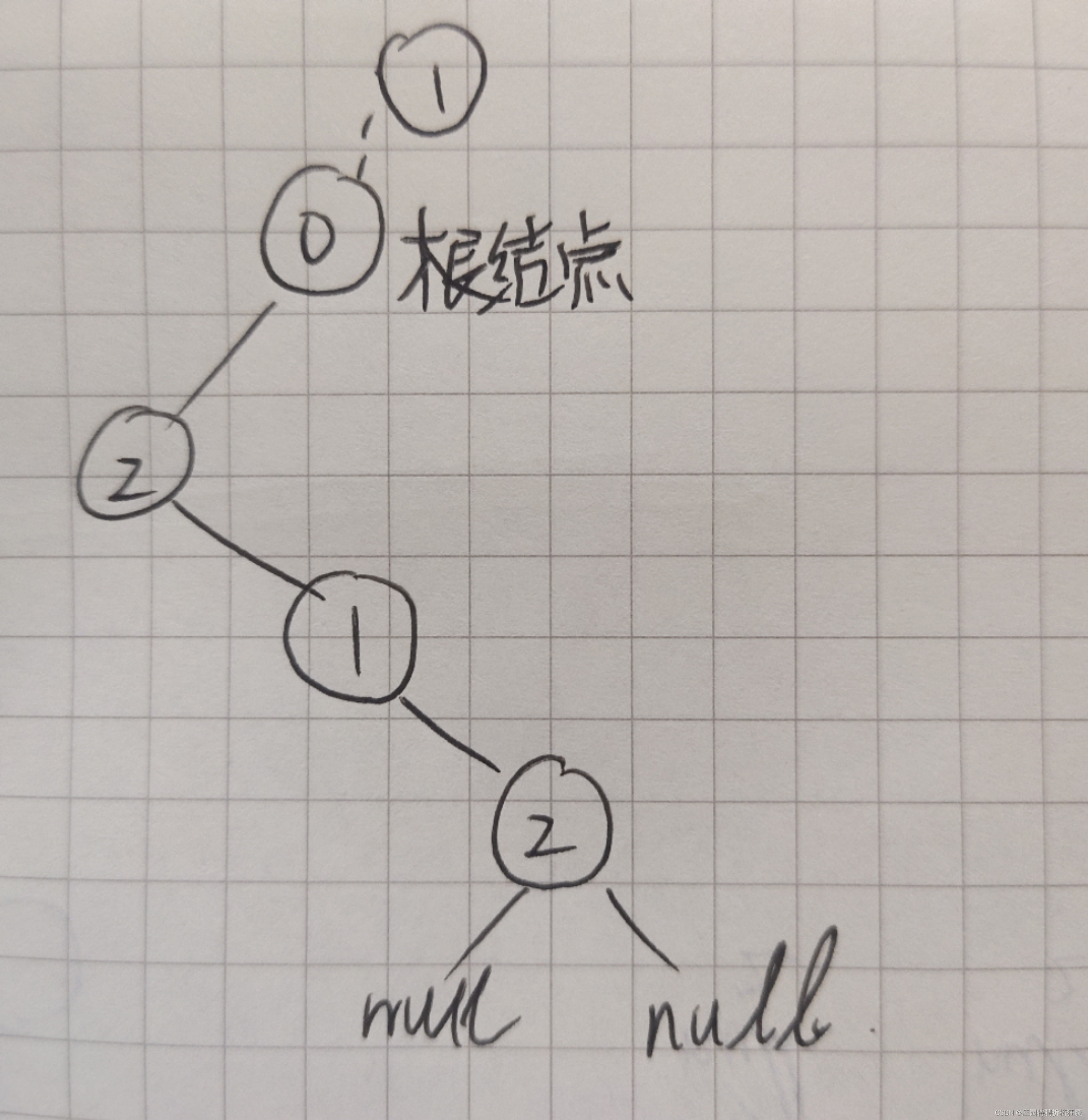
特别注意:
根节点左孩子被覆盖,按照规律若根节点有父节点应在其父节点上设置摄像头,但是根节点没有父节点,所以导致最终结束遍历时,根节点未覆盖(状态1)
所以遍历结束后应判断根节点是否为0状态,是则需要在根节点再设置一个摄像头。摄像头数目+1.
1.贪心解题
- int count=0;
- public int minCameraCover(TreeNode root) {
- int result=traversal(root);
- if(result==0) count++;
- return count;
- }
- //总是返回节点状态
- int traversal(TreeNode root){
- if(root==null) return 2;
- //后续遍历
- int left=traversal(root.left);
- int right=traversal(root.right);
- //中间状态
- if(left==0||right==0){
- count++;
- return 1;
- }
- if(left==1||right==1) return 2;
- if(left==2&&right==2) return 0;
- return -1;
- }

2.分析
时间复杂度:O(n) 遍历所有节点
空间复杂度:O(n)