蚁群算法——路径规划_蚁群算法路径规划

作者：很楠不爱3 | 2024-04-22 23:17:17

踩

蚁群算法路径规划

文章目录

参考资料
1. 简介
2. 基本思想
3. 算法精讲
4. 算法步骤
5. python实现

参考资料

1. 简介

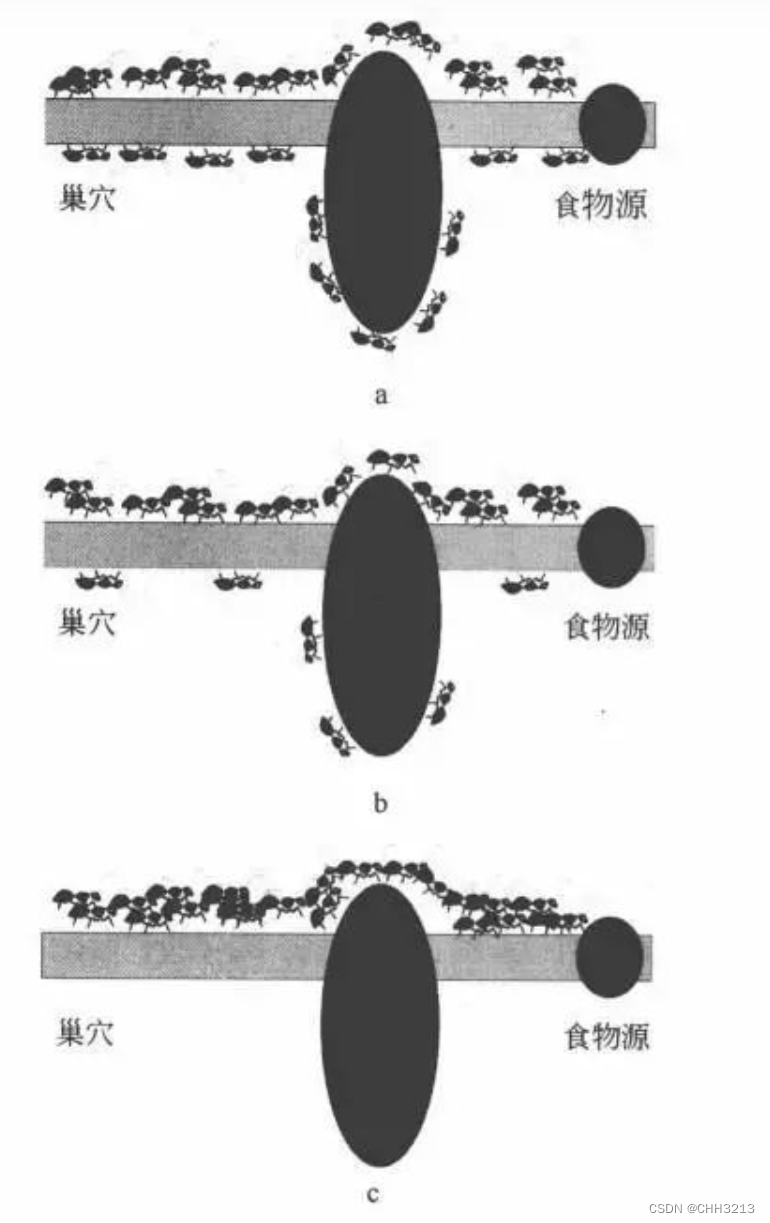
蚁群算法（Ant Colony Algorithm, ACO）于1991年首次提出，该算法模拟了自然界中蚂蚁的觅食行为。蚂蚁在寻找食物源时，会在其经过的路径上释放一种信息素，并能够感知其它蚂蚁释放的信息素。信息素浓度的大小表征路径的远近， 信息素浓度越高，表示对应的路径距离越短。通常，蚂蚁会以较大的概率优先选择信息素浓度较高的路径，并释放一定量的信息素，以增强该条路径上的信息素浓度，这样，会形成一个正反馈。最终，蚂蚁能够找到一条从巢穴到食物源的最佳路径，即距离最短。

2. 基本思想

用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。
路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多。
最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。

3. 算法精讲

不失一般性，我们定义一个具有N个节点的有权图

    G
   
   
    =
   
   
    (
   
   
    N
   
   
    ,
   
   
    A
   
   
    )
   
  
  
   G=(N,A)
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span style="margin-right: 0.10903em;" class="mord mathdefault">N</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathdefault">A</span><span class="mclose">)</span></span></span></span></span>，其中N表示节点集合<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    N
   
   
    =
   
   
    
     1
    
    
     ,
    
    
     2
    
    
     ,
    
    
     .
    
    
     .
    
    
     .
    
    
     ,
    
    
     n
    
   
  
  
   N={1,2,...,n}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span style="margin-right: 0.10903em;" class="mord mathdefault">N</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.83888em; vertical-align: -0.19444em;"></span><span class="mord"><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">.</span><span class="mord">.</span><span class="mord">.</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathdefault">n</span></span></span></span></span></span>，A表示边，<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    A
   
   
    =
   
   
    
     (
    
    
     i
    
    
     ,
    
    
     j
    
    
     )
    
    
     ∣
    
    
     i
    
    
     ,
    
    
     j
    
    
     ∈
    
    
     N
    
   
  
  
   A={(i,j)|i,j\in N}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault">A</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mopen">(</span><span class="mord mathdefault">i</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span><span class="mclose">)</span><span class="mord">∣</span><span class="mord mathdefault">i</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.277778em;"></span><span style="margin-right: 0.10903em;" class="mord mathdefault">N</span></span></span></span></span></span>。节点之间的距离（权重）设为<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    (
   
   
    
     d
    
    
     
      i
     
     
      j
     
    
   
   
    
     )
    
    
     
      n
     
     
      ×
     
     
      n
     
    
   
  
  
   (d_{ij})_{n\times n}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mclose"><span class="mclose">)</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.258331em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">n</span><span class="mbin mtight">×</span><span class="mord mathdefault mtight">n</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.208331em;"><span class=""></span></span></span></span></span></span></span></span></span></span>，<strong>目标函数</strong>即最小化起点到终点的距离之和。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161

设整个蚂蚊群体中蚂蚊的数量为

      m
     
    
    
     m
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord mathdefault">m</span></span></span></span></span>, 路径节点的数量为 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      n
     
    
    
     n
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord mathdefault">n</span></span></span></span></span>, 节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
    
    
     i
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span> 与节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      j
     
    
    
     j
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span> 之间的相互距离为 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       d
      
      
       
        i
       
       
        j
       
      
     
     
      (
     
     
      i
     
     
      ,
     
     
      j
     
     
      =
     
     
      1
     
     
      ,
     
     
      2
     
     
      ,
     
     
      …
     
     
      ,
     
     
      n
     
     
      )
     
     
      ,
     
     
      t
     
    
    
     d_{i j}(i, j=1,2, \ldots, n), t
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">i</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathdefault">n</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathdefault">t</span></span></span></span></span>时刻节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
    
    
     i
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span> 与节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      j
     
    
    
     j
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span> 连接路径上的信息素浓度为 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       τ
      
      
       
        i
       
       
        j
       
      
     
     
      (
     
     
      t
     
     
      )
     
    
    
     \tau_{i j}(t)
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">t</span><span class="mclose">)</span></span></span></span></span> 。初始时刻, 各个节点间连接路径上的信息素浓度相同, 不妨设为<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       τ
      
      
       
        i
       
       
        j
       
      
     
     
      (
     
     
      0
     
     
      )
     
     
      =
     
     
      
       τ
      
      
       0
      
     
    
    
     \tau_{i j}(0)=\tau_{0}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord">0</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.58056em; vertical-align: -0.15em;"></span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.301108em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">0</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>。</p> </li><li> <p>蚂蚁 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      k
     
     
      (
     
     
      k
     
     
      =
     
     
      1
     
     
      ,
     
     
      2
     
     
      ,
     
     
      …
     
     
      ,
     
     
      m
     
     
      )
     
    
    
     k(k=1,2, \ldots, m)
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="mopen">(</span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathdefault">m</span><span class="mclose">)</span></span></span></span></span> 根据各个节点间连接路径上的信息素浓度决定其下一个访问节点, 设 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       P
      
      
       
        i
       
       
        j
       
      
      
       k
      
     
     
      (
     
     
      t
     
     
      )
     
    
    
     P_{i j}^{k}(t)
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.24388em; vertical-align: -0.394772em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">P</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.849108em;"><span class="" style="top: -2.44134em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.394772em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">t</span><span class="mclose">)</span></span></span></span></span> 表示 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      t
     
    
    
     t
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.61508em; vertical-align: 0em;"></span><span class="mord mathdefault">t</span></span></span></span></span> 时刻蚂蚊 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      k
     
    
    
     k
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span> 从节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
    
    
     i
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span> 转移到节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      j
     
    
    
     j
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span> 的概率, 其计算公式如下:<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
       
        
         
          
           P
          
          
           
            i
           
           
            j
           
          
          
           k
          
         
         
          =
         
         
          
           {
          
          
           
            
             
              
               
                
                 
                  
                   [
                  
                  
                   
                    τ
                   
                   
                    
                     i
                    
                    
                     j
                    
                   
                  
                  
                   (
                  
                  
                   t
                  
                  
                   )
                  
                  
                   ]
                  
                 
                 
                  α
                 
                
                
                 ⋅
                
                
                 
                  
                   [
                  
                  
                   
                    η
                   
                   
                    
                     i
                    
                    
                     j
                    
                   
                  
                  
                   (
                  
                  
                   t
                  
                  
                   )
                  
                  
                   ]
                  
                 
                 
                  β
                 
                
               
               
                
                 
                  ∑
                 
                 
                  
                   s
                  
                  
                   ∈
                  
                  
                   
                    &nbsp;allow&nbsp;
                   
                   
                    k
                   
                  
                 
                
                
                 
                  
                   [
                  
                  
                   
                    τ
                   
                   
                    
                     i
                    
                    
                     s
                    
                   
                  
                  
                   (
                  
                  
                   t
                  
                  
                   )
                  
                  
                   ]
                  
                 
                 
                  α
                 
                
                
                 ⋅
                
                
                 
                  
                   [
                  
                  
                   
                    η
                   
                   
                    
                     i
                    
                    
                     s
                    
                   
                  
                  
                   (
                  
                  
                   t
                  
                  
                   )
                  
                  
                   ]
                  
                 
                 
                  β
                 
                
               
              
             
            
            
             
              
               
                s
               
               
                ∈
               
               
                
                 &nbsp;allow&nbsp;
                
                
                 k
                
               
              
             
            
           
           
            
             
              
               0
              
             
            
            
             
              
               
                s
               
               
                ∉
               
               
                
                 &nbsp;allow&nbsp;
                
                
                 k
                
               
              
             
            
           
          
         
        
       
       
       
        
         (1)
        
       
      
     
     
       \tag{1} P_{i j}^{k}= <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-1-Frame" tabindex="0" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mrow><mo>{</mo><mtable columnalign=&quot;left left&quot; rowspacing=&quot;.2em&quot; columnspacing=&quot;1em&quot; displaystyle=&quot;false&quot;><mtr><mtd><mfrac><mrow><msup><mrow><mo>[</mo><mrow><msub><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy=&quot;false&quot;>(</mo><mi>t</mi><mo stretchy=&quot;false&quot;>)</mo></mrow><mo>]</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>&amp;#x03B1;</mi></mrow></msup><mo>&amp;#x22C5;</mo><msup><mrow><mo>[</mo><mrow><msub><mi>&amp;#x03B7;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy=&quot;false&quot;>(</mo><mi>t</mi><mo stretchy=&quot;false&quot;>)</mo></mrow><mo>]</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>&amp;#x03B2;</mi></mrow></msup></mrow><mrow><munder><mo>&amp;#x2211;</mo><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>s</mi><mo>&amp;#x2208;</mo><msub><mtext>&amp;#xA0;allow&amp;#xA0;</mtext><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>k</mi></mrow></msub></mrow></munder><msup><mrow><mo>[</mo><mrow><msub><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>s</mi></mrow></msub><mo stretchy=&quot;false&quot;>(</mo><mi>t</mi><mo stretchy=&quot;false&quot;>)</mo></mrow><mo>]</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>&amp;#x03B1;</mi></mrow></msup><mo>&amp;#x22C5;</mo><msup><mrow><mo>[</mo><mrow><msub><mi>&amp;#x03B7;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>s</mi></mrow></msub><mo stretchy=&quot;false&quot;>(</mo><mi>t</mi><mo stretchy=&quot;false&quot;>)</mo></mrow><mo>]</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>&amp;#x03B2;</mi></mrow></msup></mrow></mfrac></mtd><mtd><mi>s</mi><mo>&amp;#x2208;</mo><msub><mtext>&amp;#xA0;allow&amp;#xA0;</mtext><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>k</mi></mrow></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mi>s</mi><mo>&amp;#x2209;</mo><msub><mtext>&amp;#xA0;allow&amp;#xA0;</mtext><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>k</mi></mrow></msub></mtd></mtr></mtable><mo fence=&quot;true&quot; stretchy=&quot;true&quot; symmetric=&quot;true&quot;></mo></mrow></math>" role="presentation" style="position: relative;"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-1" style="width: 100%; display: inline-block; min-width: 15.847em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.432em, 1015.54em, 6.381em, -999.997em); top: -4.655em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-2"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.432em, 1015.54em, 6.381em, -999.997em); top: -4.655em; left: 50%; margin-left: -7.743em;"><span class="mrow" id="MathJax-Span-3"><span class="mo" id="MathJax-Span-4" style="vertical-align: 2.078em;"><span style="display: inline-block; position: relative; width: 0.914em; height: 0px;"><span style="position: absolute; font-family: MathJax_Size4; top: -3.085em; left: 0em;">⎧<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; font-family: MathJax_Size4; top: -1.263em; left: 0em;">⎩<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; font-family: MathJax_Size4; top: -1.921em; left: 0em;">⎨<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mtable" id="MathJax-Span-5" style="padding-right: 0.154em; padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 14.329em; height: 0px;"><span style="position: absolute; clip: rect(2.23em, 1008.46em, 5.976em, -999.997em); top: -4.452em; left: 0em;"><span style="display: inline-block; position: relative; width: 8.457em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(2.382em, 1008.46em, 5.115em, -999.997em); top: -4.604em; left: 0em;"><span class="mtd" id="MathJax-Span-6"><span class="mrow" id="MathJax-Span-7"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.382em, 1008.46em, 5.115em, -999.997em); top: -3.997em; left: 50%; margin-left: -4.25em;"><span class="mfrac" id="MathJax-Span-8"><span style="display: inline-block; position: relative; width: 8.203em; height: 0px; margin-right: 0.104em; margin-left: 0.104em;"><span style="position: absolute; clip: rect(3.091em, 1005.01em, 4.457em, -999.997em); top: -4.705em; left: 50%; margin-left: -2.529em;"><span class="mrow" id="MathJax-Span-9"><span style="display: inline-block; position: relative; width: 5.014em; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1005.01em, 4.457em, -999.997em); top: -3.997em; left: 0em;"><span class="msubsup" id="MathJax-Span-10"><span style="display: inline-block; position: relative; width: 2.331em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1001.88em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mrow" id="MathJax-Span-11"><span class="mo" id="MathJax-Span-12" style=""><span><span style="font-size: 70.7%; font-family: MathJax_Main;">[</span></span></span><span class="mrow" id="MathJax-Span-13"><span class="msubsup" id="MathJax-Span-14"><span style="display: inline-block; position: relative; width: 0.762em; height: 0px;"><span style="position: absolute; clip: rect(3.546em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-15" style="font-size: 70.7%; font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.895em; left: 0.306em;"><span class="texatom" id="MathJax-Span-16"><span class="mrow" id="MathJax-Span-17"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.36em, 4.255em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-18" style="font-size: 50%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-19" style="font-size: 50%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-20" style="font-size: 70.7%; font-family: MathJax_Main;">(</span><span class="mi" id="MathJax-Span-21" style="font-size: 70.7%; font-family: MathJax_Math-italic;">t</span><span class="mo" id="MathJax-Span-22" style="font-size: 70.7%; font-family: MathJax_Main;">)</span></span><span class="mo" id="MathJax-Span-23" style=""><span><span style="font-size: 70.7%; font-family: MathJax_Main;">]</span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -4.351em; left: 1.926em;"><span class="texatom" id="MathJax-Span-24"><span class="mrow" id="MathJax-Span-25"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.647em, 1000.31em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-26" style="font-size: 50%; font-family: MathJax_Math-italic;">α</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-27" style="font-size: 70.7%; font-family: MathJax_Main;">⋅</span><span class="msubsup" id="MathJax-Span-28"><span style="display: inline-block; position: relative; width: 2.534em; height: 0px;"><span style="position: absolute; clip: rect(3.242em, 1002.03em, 4.457em, -999.997em); top: -3.997em; left: 0em;"><span class="mrow" id="MathJax-Span-29"><span class="mo" id="MathJax-Span-30" style="vertical-align: 0em;"><span><span style="font-size: 70.7%; font-family: MathJax_Size1;">[</span></span></span><span class="mrow" id="MathJax-Span-31"><span class="msubsup" id="MathJax-Span-32"><span style="display: inline-block; position: relative; width: 0.762em; height: 0px;"><span style="position: absolute; clip: rect(3.546em, 1000.36em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-33" style="font-size: 70.7%; font-family: MathJax_Math-italic;">η<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.794em; left: 0.357em;"><span class="texatom" id="MathJax-Span-34"><span class="mrow" id="MathJax-Span-35"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.36em, 4.255em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-36" style="font-size: 50%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-37" style="font-size: 50%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-38" style="font-size: 70.7%; font-family: MathJax_Main;">(</span><span class="mi" id="MathJax-Span-39" style="font-size: 70.7%; font-family: MathJax_Math-italic;">t</span><span class="mo" id="MathJax-Span-40" style="font-size: 70.7%; font-family: MathJax_Main;">)</span></span><span class="mo" id="MathJax-Span-41" style="vertical-align: 0em;"><span><span style="font-size: 70.7%; font-family: MathJax_Size1;">]</span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -4.402em; left: 2.179em;"><span class="texatom" id="MathJax-Span-42"><span class="mrow" id="MathJax-Span-43"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.31em, 4.255em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-44" style="font-size: 50%; font-family: MathJax_Math-italic;">β<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.141em, 1008.1em, 4.559em, -999.997em); top: -3.389em; left: 50%; margin-left: -4.047em;"><span class="mrow" id="MathJax-Span-45"><span style="display: inline-block; position: relative; width: 8.102em; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1008.1em, 4.559em, -999.997em); top: -3.997em; left: 0em;"><span class="munderover" id="MathJax-Span-46"><span style="display: inline-block; position: relative; width: 3.04em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1000.71em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-47" style="font-size: 70.7%; font-family: MathJax_Size1; vertical-align: 0em;">∑</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.794em; left: 0.762em;"><span class="texatom" id="MathJax-Span-48"><span class="mrow" id="MathJax-Span-49"><span style="display: inline-block; position: relative; width: 2.281em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1002.28em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-50" style="font-size: 50%; font-family: MathJax_Math-italic;">s</span><span class="mo" id="MathJax-Span-51" style="font-size: 50%; font-family: MathJax_Main;">∈</span><span class="msubsup" id="MathJax-Span-52"><span style="display: inline-block; position: relative; width: 1.673em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1001.27em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mtext" id="MathJax-Span-53" style="font-size: 50%; font-family: MathJax_Main;">&nbsp;allow&nbsp;</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 1.369em;"><span class="texatom" id="MathJax-Span-54"><span class="mrow" id="MathJax-Span-55"><span style="display: inline-block; position: relative; width: 0.256em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.26em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-56" style="font-size: 50%; font-family: MathJax_Math-italic;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-57" style="padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 2.331em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1001.88em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mrow" id="MathJax-Span-58"><span class="mo" id="MathJax-Span-59" style="font-size: 70.7%; font-family: MathJax_Main;">[</span><span class="mrow" id="MathJax-Span-60"><span class="msubsup" id="MathJax-Span-61"><span style="display: inline-block; position: relative; width: 0.762em; height: 0px;"><span style="position: absolute; clip: rect(3.546em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-62" style="font-size: 70.7%; font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.895em; left: 0.306em;"><span class="texatom" id="MathJax-Span-63"><span class="mrow" id="MathJax-Span-64"><span style="display: inline-block; position: relative; width: 0.408em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.41em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-65" style="font-size: 50%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-66" style="font-size: 50%; font-family: MathJax_Math-italic;">s</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-67" style="font-size: 70.7%; font-family: MathJax_Main;">(</span><span class="mi" id="MathJax-Span-68" style="font-size: 70.7%; font-family: MathJax_Math-italic;">t</span><span class="mo" id="MathJax-Span-69" style="font-size: 70.7%; font-family: MathJax_Main;">)</span></span><span class="mo" id="MathJax-Span-70" style="font-size: 70.7%; font-family: MathJax_Main;">]</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -4.351em; left: 1.977em;"><span class="texatom" id="MathJax-Span-71"><span class="mrow" id="MathJax-Span-72"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.647em, 1000.31em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-73" style="font-size: 50%; font-family: MathJax_Math-italic;">α</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-74" style="font-size: 70.7%; font-family: MathJax_Main;">⋅</span><span class="msubsup" id="MathJax-Span-75"><span style="display: inline-block; position: relative; width: 2.331em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1001.93em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mrow" id="MathJax-Span-76"><span class="mo" id="MathJax-Span-77" style=""><span><span style="font-size: 70.7%; font-family: MathJax_Main;">[</span></span></span><span class="mrow" id="MathJax-Span-78"><span class="msubsup" id="MathJax-Span-79"><span style="display: inline-block; position: relative; width: 0.812em; height: 0px;"><span style="position: absolute; clip: rect(3.546em, 1000.36em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-80" style="font-size: 70.7%; font-family: MathJax_Math-italic;">η<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.794em; left: 0.357em;"><span class="texatom" id="MathJax-Span-81"><span class="mrow" id="MathJax-Span-82"><span style="display: inline-block; position: relative; width: 0.408em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.41em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-83" style="font-size: 50%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-84" style="font-size: 50%; font-family: MathJax_Math-italic;">s</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-85" style="font-size: 70.7%; font-family: MathJax_Main;">(</span><span class="mi" id="MathJax-Span-86" style="font-size: 70.7%; font-family: MathJax_Math-italic;">t</span><span class="mo" id="MathJax-Span-87" style="font-size: 70.7%; font-family: MathJax_Main;">)</span></span><span class="mo" id="MathJax-Span-88" style=""><span><span style="font-size: 70.7%; font-family: MathJax_Main;">]</span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -4.351em; left: 2.027em;"><span class="texatom" id="MathJax-Span-89"><span class="mrow" id="MathJax-Span-90"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.495em, 1000.31em, 4.255em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-91" style="font-size: 50%; font-family: MathJax_Math-italic;">β<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(0.863em, 1008.2em, 1.217em, -999.997em); top: -1.263em; left: 0em;"><span style="display: inline-block; overflow: hidden; vertical-align: 0em; border-top: 1.3px solid; width: 8.203em; height: 0px;"></span><span style="display: inline-block; width: 0px; height: 1.066em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.192em, 1000.46em, 4.154em, -999.997em); top: -2.63em; left: 0em;"><span class="mtd" id="MathJax-Span-101"><span class="mrow" id="MathJax-Span-102"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.46em, 4.154em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.251em;"><span class="mn" id="MathJax-Span-103" style="font-family: MathJax_Main;">0</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.457em;"></span></span><span style="position: absolute; clip: rect(2.534em, 1004.86em, 5.723em, -999.997em); top: -3.997em; left: 9.469em;"><span style="display: inline-block; position: relative; width: 4.862em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.141em, 1004.86em, 4.305em, -999.997em); top: -4.604em; left: 0em;"><span class="mtd" id="MathJax-Span-92"><span class="mrow" id="MathJax-Span-93"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1004.86em, 4.305em, -999.997em); top: -3.997em; left: 50%; margin-left: -2.427em;"><span class="mi" id="MathJax-Span-94" style="font-family: MathJax_Math-italic;">s</span><span class="mo" id="MathJax-Span-95" style="font-family: MathJax_Main; padding-left: 0.256em;">∈</span><span class="msubsup" id="MathJax-Span-96" style="padding-left: 0.256em;"><span style="display: inline-block; position: relative; width: 3.242em; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1002.53em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mtext" id="MathJax-Span-97" style="font-family: MathJax_Main;">&nbsp;allow&nbsp;</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 2.787em;"><span class="texatom" id="MathJax-Span-98"><span class="mrow" id="MathJax-Span-99"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-100" style="font-size: 70.7%; font-family: MathJax_Math-italic;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.141em, 1004.86em, 4.356em, -999.997em); top: -2.63em; left: 0em;"><span class="mtd" id="MathJax-Span-104"><span class="mrow" id="MathJax-Span-105"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1004.86em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -2.427em;"><span class="mi" id="MathJax-Span-106" style="font-family: MathJax_Math-italic;">s</span><span class="mo" id="MathJax-Span-107" style="font-family: MathJax_Main; padding-left: 0.256em;">∉</span><span class="msubsup" id="MathJax-Span-108" style="padding-left: 0.256em;"><span style="display: inline-block; position: relative; width: 3.242em; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1002.53em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mtext" id="MathJax-Span-109" style="font-family: MathJax_Main;">&nbsp;allow&nbsp;</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 2.787em;"><span class="texatom" id="MathJax-Span-110"><span class="mrow" id="MathJax-Span-111"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-112" style="font-size: 70.7%; font-family: MathJax_Math-italic;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-113"></span></span><span style="display: inline-block; width: 0px; height: 4.66em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.66em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.65em; border-left: 0px solid; width: 0px; height: 3.824em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mfrac><mrow><msup><mrow><mo>[</mo><mrow><msub><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo></mrow><mo>]</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mi>α</mi></mrow></msup><mo>⋅</mo><msup><mrow><mo>[</mo><mrow><msub><mi>η</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo></mrow><mo>]</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mi>β</mi></mrow></msup></mrow><mrow><munder><mo>∑</mo><mrow class="MJX-TeXAtom-ORD"><mi>s</mi><mo>∈</mo><msub><mtext>&nbsp;allow&nbsp;</mtext><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msub></mrow></munder><msup><mrow><mo>[</mo><mrow><msub><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>s</mi></mrow></msub><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo></mrow><mo>]</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mi>α</mi></mrow></msup><mo>⋅</mo><msup><mrow><mo>[</mo><mrow><msub><mi>η</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>s</mi></mrow></msub><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo></mrow><mo>]</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mi>β</mi></mrow></msup></mrow></mfrac></mtd><mtd><mi>s</mi><mo>∈</mo><msub><mtext>&nbsp;allow&nbsp;</mtext><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msub></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mi>s</mi><mo>∉</mo><msub><mtext>&nbsp;allow&nbsp;</mtext><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msub></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-1">\begin{cases}\frac{\left[\tau_{i j}(t)\right]^{\alpha} \cdot\left[\eta_{i j}(t)\right]^{\beta}}{\sum_{s \in \text { allow }_{k}}\left[\tau_{i s}(t)\right]^{\alpha} \cdot\left[\eta_{i s}(t)\right]^{\beta}} & s \in \text { allow }_{k} \\ 0 & s \notin \text { allow }_{k}\end{cases}</script> 
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28222em; vertical-align: -0.383108em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">P</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.899108em;"><span class="" style="top: -2.453em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.383108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 3.60004em; vertical-align: -1.55002em;"></span><span class="minner"><span class="mopen"><span class="delimsizing mult"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.05002em;"><span class="" style="top: -2.49999em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎩</span></span></span><span class="" style="top: -3.15001em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎨</span></span></span><span class="" style="top: -4.30002em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎧</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.55002em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mtable"><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.96564em;"><span class="" style="top: -3.96564em;"><span class="pstrut" style="height: 3.15624em;"></span><span class="mord"><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.15624em;"><span class="" style="top: -2.56478em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mop mtight"><span class="mop op-symbol small-op mtight" style="position: relative; top: -0.000005em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.17459em;"><span class="" style="top: -2.17856em; margin-left: 0em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">s</span><span class="mrel mtight">∈</span><span class="mord mtight"><span class="mord text mtight"><span class="mord mtight">&nbsp;allow&nbsp;</span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.3448em;"><span class="" style="top: -2.3448em; margin-right: 0.1em;"><span class="pstrut" style="height: 2.69444em;"></span><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.34964em;"><span class=""></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.571181em;"><span class=""></span></span></span></span></span></span><span class="minner mtight"><span class="minner mtight"><span class="mopen mtight delimcenter" style="top: 0em;"><span class="mtight">[</span></span><span class="mord mtight"><span style="margin-right: 0.1132em;" class="mord mathdefault mtight">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.328086em;"><span class="" style="top: -2.357em; margin-left: -0.1132em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mord mathdefault mtight">s</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span><span class="mopen mtight">(</span><span class="mord mathdefault mtight">t</span><span class="mclose mtight">)</span><span class="mclose mtight delimcenter" style="top: 0em;"><span class="mtight">]</span></span></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.704686em;"><span class="" style="top: -2.89714em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span style="margin-right: 0.0037em;" class="mord mathdefault mtight">α</span></span></span></span></span></span></span></span></span><span class="mbin mtight">⋅</span><span class="minner mtight"><span class="minner mtight"><span class="mopen mtight delimcenter" style="top: 0em;"><span class="mtight">[</span></span><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">η</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.328086em;"><span class="" style="top: -2.357em; margin-left: -0.03588em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mord mathdefault mtight">s</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.143em;"><span class=""></span></span></span></span></span></span><span class="mopen mtight">(</span><span class="mord mathdefault mtight">t</span><span class="mclose mtight">)</span><span class="mclose mtight delimcenter" style="top: 0em;"><span class="mtight">]</span></span></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.893171em;"><span class="" style="top: -2.89714em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span style="margin-right: 0.05278em;" class="mord mathdefault mtight">β</span></span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.50732em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="minner mtight"><span class="minner mtight"><span class="mopen mtight delimcenter" style="top: 0em;"><span class="mtight">[</span></span><span class="mord mtight"><span style="margin-right: 0.1132em;" class="mord mathdefault mtight">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.328086em;"><span class="" style="top: -2.357em; margin-left: -0.1132em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.281886em;"><span class=""></span></span></span></span></span></span><span class="mopen mtight">(</span><span class="mord mathdefault mtight">t</span><span class="mclose mtight">)</span><span class="mclose mtight delimcenter" style="top: 0em;"><span class="mtight">]</span></span></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.738543em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span style="margin-right: 0.0037em;" class="mord mathdefault mtight">α</span></span></span></span></span></span></span></span></span><span class="mbin mtight">⋅</span><span class="minner mtight"><span class="minner mtight"><span class="mopen mtight delimcenter" style="top: 0em;"><span class="mtight">[</span></span><span class="mord mtight"><span style="margin-right: 0.03588em;" class="mord mathdefault mtight">η</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.328086em;"><span class="" style="top: -2.357em; margin-left: -0.03588em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.281886em;"><span class=""></span></span></span></span></span></span><span class="mopen mtight">(</span><span class="mord mathdefault mtight">t</span><span class="mclose mtight">)</span><span class="mclose mtight delimcenter" style="top: 0em;"><span class="mtight">]</span></span></span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.927029em;"><span class="" style="top: -2.931em; margin-right: 0.0714286em;"><span class="pstrut" style="height: 2.5em;"></span><span class="sizing reset-size3 size1 mtight"><span class="mord mtight"><span style="margin-right: 0.05278em;" class="mord mathdefault mtight">β</span></span></span></span></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.835047em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span><span class="" style="top: -2.1226em;"><span class="pstrut" style="height: 3.15624em;"></span><span class="mord"><span class="mord">0</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.46564em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 1em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.96564em;"><span class="" style="top: -3.96564em;"><span class="pstrut" style="height: 3.15624em;"></span><span class="mord"><span class="mord mathdefault">s</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mord"><span class="mord text"><span class="mord">&nbsp;allow&nbsp;</span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -2.1226em;"><span class="pstrut" style="height: 3.15624em;"></span><span class="mord"><span class="mord mathdefault">s</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel"><span class="mord"><span class="mrel">∈</span></span><span class="mord"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.75em;"><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class="llap"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="inner"><span class="mord"><span class="mord">/</span><span class="mspace" style="margin-right: 0.0555556em;"></span></span></span><span class="fix"></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.25em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mord"><span class="mord text"><span class="mord">&nbsp;allow&nbsp;</span></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.46564em;"><span class=""></span></span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span><span class="tag"><span class="strut" style="height: 3.60004em; vertical-align: -1.55002em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">1</span></span><span class="mord">)</span></span></span></span></span></span></span></p> <p>其中,</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611

        η
       
       
        
         i
        
        
         j
        
       
      
      
       (
      
      
       t
      
      
       )
      
     
     
      \eta_{i j}(t)
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">η</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">t</span><span class="mclose">)</span></span></span></span></span> 为<strong>启发函数</strong>, <span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
        η
       
       
        
         i
        
        
         j
        
       
      
      
       (
      
      
       t
      
      
       )
      
      
       =
      
      
       1
      
      
       /
      
      
       
        d
       
       
        
         i
        
        
         j
        
       
      
     
     
      \eta_{i j}(t)=1 / d_{i j}
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">η</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">t</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord">1</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>, 表示蚂蚊从节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       i
      
     
     
      i
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span> 转移到节点 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       j
      
     
     
      j
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span> 的期望程度，</li><li><span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       a
      
      
       l
      
      
       l
      
      
       o
      
      
       
        w
       
       
        k
       
      
      
       (
      
      
       k
      
      
       =
      
      
       1
      
      
       ,
      
      
       2
      
      
       ,
      
      
       …
      
      
       ,
      
      
       m
      
      
       )
      
     
     
      allow_{k}(k=1,2, \ldots, m)
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault">a</span><span style="margin-right: 0.01968em;" class="mord mathdefault">l</span><span style="margin-right: 0.01968em;" class="mord mathdefault">l</span><span class="mord mathdefault">o</span><span class="mord"><span style="margin-right: 0.02691em;" class="mord mathdefault">w</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: -0.02691em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord mathdefault">m</span><span class="mclose">)</span></span></span></span></span> 为蚂蚁<span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       k
      
     
     
      k
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>待访问节点的集合。开始时, <span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       a
      
      
       l
      
      
       l
      
      
       o
      
      
       
        w
       
       
        k
       
      
     
     
      allow_{k}
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.84444em; vertical-align: -0.15em;"></span><span class="mord mathdefault">a</span><span style="margin-right: 0.01968em;" class="mord mathdefault">l</span><span style="margin-right: 0.01968em;" class="mord mathdefault">l</span><span class="mord mathdefault">o</span><span class="mord"><span style="margin-right: 0.02691em;" class="mord mathdefault">w</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: -0.02691em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>中有(n-1)个元素,即包括除了蚂蚁<span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       k
      
     
     
      k
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>出发节点的其它所有节点。随着时间的推进, allow <span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
       
        k
       
      
     
     
      _{k}
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.486108em; vertical-align: -0.15em;"></span><span class="mord"><span class=""></span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span> 中的元素不断减少, 直至为空, 即表示所有的节点均访问完毕。</li><li><span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       α
      
     
     
      \alpha
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span></span></span> 为<strong>信息素重要程度因子</strong>, 其值越大, 蚂蚁选择之前走过的路径可能性就越大,搜索路径的随机性减弱, 其值越小,蚁群搜索范围就会减少,容易陷入局部最优。一般取值范围为<span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       [
      
      
       0
      
      
       ,
      
      
       5
      
      
       ]
      
     
     
      [0,5]
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">5</span><span class="mclose">]</span></span></span></span></span>。</li><li><span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       β
      
     
     
      \beta
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.88888em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05278em;" class="mord mathdefault">β</span></span></span></span></span> 为<strong>启发函数重要程度因子</strong>, 其值越大, 表示启发函数在转移中的作用越大, 即蚂蚊会以较大的摡率转移到距离短的节点，蚁群就越容易选择局部较短路径,这时算法的收敛速度是加快了，但是随机性却不高，容易得到局部的相对最优。一般取值范围为<span class="katex--inline"><span class="katex"><span class="katex-mathml">
   
    
     
      
       [
      
      
       0
      
      
       ,
      
      
       5
      
      
       ]
      
     
     
      [0,5]
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">5</span><span class="mclose">]</span></span></span></span></span>。</li></ul> </li><li> <p>计算完节点间的转移概率后，采用与遗传算法中一样的<strong>轮盘赌方法</strong>选择下一个待访问的节点。</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305

依据轮盘赌法来选择下一个待访问的节点，而不是直接按概率大小选择，是因为这样可以扩大搜索范围，进而寻找全局最优，避免陷入局部最优。

首先计算每个个体的累积概率

       q
      
      
       j
      
     
    
    
     q_{j}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span> ，如下式:<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
       
        
         
          
           q
          
          
           j
          
         
         
          =
         
         
          
           ∑
          
          
           
            j
           
           
            =
           
           
            1
           
          
          
           l
          
         
         
          
           P
          
          
           
            i
           
           
            j
           
          
          
           k
          
         
        
       
       
       
        
         (2)
        
       
      
     
     
       \tag{2} q_{j}=\sum_{j=1}^{l} P_{i j}^{k} 
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 3.24989em; vertical-align: -1.41378em;"></span><span class="mop op-limits"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.83611em;"><span class="" style="top: -1.87233em; margin-left: 0em;"><span class="pstrut" style="height: 3.05em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span><span class="mrel mtight">=</span><span class="mord mtight">1</span></span></span></span><span class="" style="top: -3.05001em;"><span class="pstrut" style="height: 3.05em;"></span><span class=""><span class="mop op-symbol large-op">∑</span></span></span><span class="" style="top: -4.30001em; margin-left: 0em;"><span class="pstrut" style="height: 3.05em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.01968em;" class="mord mathdefault mtight">l</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.41378em;"><span class=""></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span style="margin-right: 0.13889em;" class="mord mathdefault">P</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.899108em;"><span class="" style="top: -2.453em; margin-left: -0.13889em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.383108em;"><span class=""></span></span></span></span></span></span></span><span class="tag"><span class="strut" style="height: 3.24989em; vertical-align: -1.41378em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">2</span></span><span class="mord">)</span></span></span></span></span></span></span><br> <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       q
      
      
       j
      
     
    
    
     q_{j}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span> 相当于转盘上的跨度，跨度越大的区域越容易选到，<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      l
     
    
    
     l
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.01968em;" class="mord mathdefault">l</span></span></span></span></span>代表下一步可选路径的数量。<br> 之后随机生成一个 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      (
     
     
      0
     
     
      ，
     
     
      1
     
     
      )
     
    
    
     (0 ， 1)
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">0</span><span class="mord cjk_fallback">，</span><span class="mord">1</span><span class="mclose">)</span></span></span></span></span> 的小数<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      r
     
    
    
     \mathrm{r}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord"><span class="mord mathrm">r</span></span></span></span></span></span>，比较所有 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       q
      
      
       j
      
     
    
    
     q_{j}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span> 与 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      r
     
    
    
     \mathrm{r}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord"><span class="mord mathrm">r</span></span></span></span></span></span> 的大小，选出大于 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      r
     
    
    
     r
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span></span></span></span></span> 的最小的那个 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       q
      
      
       j
      
     
     
      ，
     
    
    
     q_{j} ，
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mord cjk_fallback">，</span></span></span></span></span> 该 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       q
      
      
       j
      
     
    
    
     q_{j}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.716668em; vertical-align: -0.286108em;"></span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span> 对应的索引 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      j
     
    
    
     j
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span>即为第 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      k
     
    
    
     \mathrm{k}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord"><span class="mord mathrm">k</span></span></span></span></span></span> 只蚂蚁在第<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
    
    
     i
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span>条路径时下一步要选择的目标点。<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
       
        
         
          
           
            
             
              r
             
             
              =
             
             
              rand
             
             
              ⁡
             
             
              (
             
             
              0
             
             
              ,
             
             
              1
             
             
              )
             
            
           
          
         
         
          
           
            
             
              j
             
             
              =
             
             
              index
             
             
              ⁡
             
             
              
               {
              
              
               min
              
              
               ⁡
              
              
               
                [
               
               
                
                 q
                
                
                 j
                
               
               
                &gt;
               
               
                r
               
               
                ]
               
              
              
               }
              
             
            
           
          
         
        
       
       
       
        
         (3)
        
       
      
     
     
       \tag{3} <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-2-Frame" tabindex="0" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mtable rowspacing=&quot;3pt&quot; columnspacing=&quot;1em&quot; displaystyle=&quot;true&quot;><mtr><mtd><mi>r</mi><mo>=</mo><mi>rand</mi><mo>&amp;#x2061;</mo><mo stretchy=&quot;false&quot;>(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo stretchy=&quot;false&quot;>)</mo></mtd></mtr><mtr><mtd><mi>j</mi><mo>=</mo><mi>index</mi><mo>&amp;#x2061;</mo><mrow><mo>{</mo><mrow><mo movablelimits=&quot;true&quot; form=&quot;prefix&quot;>min</mo><mrow><mo>[</mo><mrow><msub><mi>q</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>j</mi></mrow></msub><mo>&amp;gt;</mo><mi>r</mi></mrow><mo>]</mo></mrow></mrow><mo>}</mo></mrow></mtd></mtr></mtable></math>" role="presentation" style="position: relative;"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-114" style="width: 100%; display: inline-block; min-width: 10.33em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.382em, 1010.08em, 5.115em, -999.997em); top: -3.997em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-115"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.382em, 1010.08em, 5.115em, -999.997em); top: -3.997em; left: 50%; margin-left: -5.06em;"><span class="mtable" id="MathJax-Span-116" style="padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 9.975em; height: 0px;"><span style="position: absolute; clip: rect(2.432em, 1009.92em, 5.115em, -999.997em); top: -3.997em; left: 0em;"><span style="display: inline-block; position: relative; width: 9.975em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.091em, 1005.88em, 4.407em, -999.997em); top: -4.655em; left: 0em;"><span class="mtd" id="MathJax-Span-117"><span class="mrow" id="MathJax-Span-118"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1005.88em, 4.407em, -999.997em); top: -3.997em; left: 50%; margin-left: -2.984em;"><span class="mi" id="MathJax-Span-119" style="font-family: MathJax_Math-italic;">r</span><span class="mo" id="MathJax-Span-120" style="font-family: MathJax_Main; padding-left: 0.256em;">=</span><span class="mi" id="MathJax-Span-121" style="font-family: MathJax_Main; padding-left: 0.256em;">rand</span><span class="mo" id="MathJax-Span-122"></span><span class="mo" id="MathJax-Span-123" style="font-family: MathJax_Main;">(</span><span class="mn" id="MathJax-Span-124" style="font-family: MathJax_Main;">0</span><span class="mo" id="MathJax-Span-125" style="font-family: MathJax_Main;">,</span><span class="mn" id="MathJax-Span-126" style="font-family: MathJax_Main; padding-left: 0.154em;">1</span><span class="mo" id="MathJax-Span-127" style="font-family: MathJax_Main;">)</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.091em, 1009.92em, 4.457em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-128"><span class="mrow" id="MathJax-Span-129"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1009.92em, 4.457em, -999.997em); top: -3.997em; left: 50%; margin-left: -5.009em;"><span class="mi" id="MathJax-Span-130" style="font-family: MathJax_Math-italic;">j</span><span class="mo" id="MathJax-Span-131" style="font-family: MathJax_Main; padding-left: 0.256em;">=</span><span class="mi" id="MathJax-Span-132" style="font-family: MathJax_Main; padding-left: 0.256em;">index</span><span class="mo" id="MathJax-Span-133"></span><span class="mrow" id="MathJax-Span-134"><span class="mo" id="MathJax-Span-135" style=""><span style="font-family: MathJax_Main;">{</span></span><span class="mrow" id="MathJax-Span-136"><span class="mo" id="MathJax-Span-137" style="font-family: MathJax_Main;">min</span><span class="mrow" id="MathJax-Span-138" style="padding-left: 0.154em;"><span class="mo" id="MathJax-Span-139" style=""><span style="font-family: MathJax_Main;">[</span></span><span class="mrow" id="MathJax-Span-140"><span class="msubsup" id="MathJax-Span-141"><span style="display: inline-block; position: relative; width: 0.812em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.46em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-142" style="font-family: MathJax_Math-italic;">q<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.458em;"><span class="texatom" id="MathJax-Span-143"><span class="mrow" id="MathJax-Span-144"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-145" style="font-size: 70.7%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-146" style="font-family: MathJax_Main; padding-left: 0.256em;">&gt;</span><span class="mi" id="MathJax-Span-147" style="font-family: MathJax_Math-italic; padding-left: 0.256em;">r</span></span><span class="mo" id="MathJax-Span-148" style=""><span style="font-family: MathJax_Main;">]</span></span></span></span><span class="mo" id="MathJax-Span-149" style=""><span style="font-family: MathJax_Main;">}</span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.03em; border-left: 0px solid; width: 0px; height: 2.584em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable rowspacing="3pt" columnspacing="1em" displaystyle="true"><mtr><mtd><mi>r</mi><mo>=</mo><mi>rand</mi><mo>⁡</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mn>1</mn><mo stretchy="false">)</mo></mtd></mtr><mtr><mtd><mi>j</mi><mo>=</mo><mi>index</mi><mo>⁡</mo><mrow><mo>{</mo><mrow><mo movablelimits="true" form="prefix">min</mo><mrow><mo>[</mo><mrow><msub><mi>q</mi><mrow class="MJX-TeXAtom-ORD"><mi>j</mi></mrow></msub><mo>&gt;</mo><mi>r</mi></mrow><mo>]</mo></mrow></mrow><mo>}</mo></mrow></mtd></mtr></mtable></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-2">\begin{gathered} r=\operatorname{rand}(0,1) \\ j=\operatorname{index}\left\{\min \left[q_{j}>r\right]\right\} \end{gathered}</script> 
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 3em; vertical-align: -1.25em;"></span><span class="mord"><span class="mtable"><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.75em;"><span class="" style="top: -3.91em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mop"><span class="mord mathrm">r</span><span class="mord mathrm">a</span><span class="mord mathrm">n</span><span class="mord mathrm">d</span></span><span class="mopen">(</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">1</span><span class="mclose">)</span></span></span><span class="" style="top: -2.41em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mop"><span class="mord mathrm">i</span><span class="mord mathrm">n</span><span class="mord mathrm">d</span><span class="mord mathrm">e</span><span class="mord mathrm">x</span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;">{<!-- --></span><span class="mop">min</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;">[</span><span class="mord"><span style="margin-right: 0.03588em;" class="mord mathdefault">q</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">&gt;</span><span class="mspace" style="margin-right: 0.277778em;"></span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mclose delimcenter" style="top: 0em;">]</span></span><span class="mclose delimcenter" style="top: 0em;">}</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.25em;"><span class=""></span></span></span></span></span></span></span></span><span class="tag"><span class="strut" style="height: 3em; vertical-align: -1.25em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">3</span></span><span class="mord">)</span></span></span></span></span></span></span></p> </li><li> <p>在蚂蚁释放信息素的同时，各个节点间连接路径上的信息素逐渐消失,设参数<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      ρ
     
     
      (
     
     
      0
     
     
      &lt;
     
     
      ρ
     
     
      &lt;
     
     
      1
     
     
      ，
     
     
      一
     
     
      般
     
     
      取
     
     
      值
     
     
      为
     
     
      0.1
     
    
    
     \rho(0&lt;\rho&lt;1，一般取值为0.1
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault">ρ</span><span class="mopen">(</span><span class="mord">0</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">&lt;</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.73354em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">ρ</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">&lt;</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.64444em; vertical-align: 0em;"></span><span class="mord">1</span><span class="mord cjk_fallback">，</span><span class="mord cjk_fallback">一</span><span class="mord cjk_fallback">般</span><span class="mord cjk_fallback">取</span><span class="mord cjk_fallback">值</span><span class="mord cjk_fallback">为</span><span class="mord">0</span><span class="mord">.</span><span class="mord">1</span></span></span></span></span>~<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      0.99
     
     
      )
     
    
    
     0.99)
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">9</span><span class="mord">9</span><span class="mclose">)</span></span></span></span></span>表示 <strong>信息素的挥发程度</strong>。当所有的蚂蚁完成一次循环后，各个节点间链接路径上的信息素浓度需进行更新，计算公式为<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
       
        
         
          {
         
         
          
           
            
             
              
               
                τ
               
               
                
                 i
                
                
                 j
                
               
              
              
               (
              
              
               t
              
              
               +
              
              
               1
              
              
               )
              
              
               =
              
              
               (
              
              
               1
              
              
               −
              
              
               ρ
              
              
               )
              
              
               
                τ
               
               
                
                 i
                
                
                 j
                
               
              
              
               (
              
              
               t
              
              
               )
              
              
               +
              
              
               Δ
              
              
               
                τ
               
               
                
                 i
                
                
                 j
                
               
              
             
            
           
          
          
           
            
             
              
               Δ
              
              
               
                τ
               
               
                
                 i
                
                
                 j
                
               
              
              
               =
              
              
               
                ∑
               
               
                
                 k
                
                
                 =
                
                
                 1
                
               
               
                n
               
              
              
               Δ
              
              
               
                τ
               
               
                
                 i
                
                
                 j
                
               
               
                k
               
              
             
            
           
          
         
        
       
       
       
        
         (4)
        
       
      
     
     
       \tag{4} \left\{<span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-3-Frame" tabindex="0" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mtable columnalign=&quot;left&quot; rowspacing=&quot;4pt&quot; columnspacing=&quot;1em&quot;><mtr><mtd><msub><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy=&quot;false&quot;>(</mo><mi>t</mi><mo>+</mo><mn>1</mn><mo stretchy=&quot;false&quot;>)</mo><mo>=</mo><mo stretchy=&quot;false&quot;>(</mo><mn>1</mn><mo>&amp;#x2212;</mo><mi>&amp;#x03C1;</mi><mo stretchy=&quot;false&quot;>)</mo><msub><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy=&quot;false&quot;>(</mo><mi>t</mi><mo stretchy=&quot;false&quot;>)</mo><mo>+</mo><mi mathvariant=&quot;normal&quot;>&amp;#x0394;</mi><msub><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow></msub></mtd></mtr><mtr><mtd><mi mathvariant=&quot;normal&quot;>&amp;#x0394;</mi><msub><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow></msub><mo>=</mo><munderover><mo>&amp;#x2211;</mo><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>k</mi><mo>=</mo><mn>1</mn></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>n</mi></mrow></munderover><mi mathvariant=&quot;normal&quot;>&amp;#x0394;</mi><msubsup><mi>&amp;#x03C4;</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>i</mi><mi>j</mi></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>k</mi></mrow></msubsup></mtd></mtr></mtable></math>" role="presentation" style="position: relative;"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-150" style="width: 100%; display: inline-block; min-width: 13.873em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.23em, 1013.57em, 5.318em, -999.997em); top: -3.997em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-151"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.23em, 1013.57em, 5.318em, -999.997em); top: -3.997em; left: 50%; margin-left: -6.781em;"><span class="mtable" id="MathJax-Span-152" style="padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 13.418em; height: 0px;"><span style="position: absolute; clip: rect(2.281em, 1013.42em, 5.318em, -999.997em); top: -3.997em; left: 0em;"><span style="display: inline-block; position: relative; width: 13.418em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.091em, 1013.42em, 4.457em, -999.997em); top: -4.857em; left: 0em;"><span class="mtd" id="MathJax-Span-153"><span class="mrow" id="MathJax-Span-154"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1013.42em, 4.457em, -999.997em); top: -3.997em; left: 50%; margin-left: -6.68em;"><span class="msubsup" id="MathJax-Span-155"><span style="display: inline-block; position: relative; width: 1.066em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-156" style="font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.104em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.458em;"><span class="texatom" id="MathJax-Span-157"><span class="mrow" id="MathJax-Span-158"><span style="display: inline-block; position: relative; width: 0.559em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-159" style="font-size: 70.7%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-160" style="font-size: 70.7%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-161" style="font-family: MathJax_Main;">(</span><span class="mi" id="MathJax-Span-162" style="font-family: MathJax_Math-italic;">t</span><span class="mo" id="MathJax-Span-163" style="font-family: MathJax_Main; padding-left: 0.205em;">+</span><span class="mn" id="MathJax-Span-164" style="font-family: MathJax_Main; padding-left: 0.205em;">1</span><span class="mo" id="MathJax-Span-165" style="font-family: MathJax_Main;">)</span><span class="mo" id="MathJax-Span-166" style="font-family: MathJax_Main; padding-left: 0.256em;">=</span><span class="mo" id="MathJax-Span-167" style="font-family: MathJax_Main; padding-left: 0.256em;">(</span><span class="mn" id="MathJax-Span-168" style="font-family: MathJax_Main;">1</span><span class="mo" id="MathJax-Span-169" style="font-family: MathJax_Main; padding-left: 0.205em;">−</span><span class="mi" id="MathJax-Span-170" style="font-family: MathJax_Math-italic; padding-left: 0.205em;">ρ</span><span class="mo" id="MathJax-Span-171" style="font-family: MathJax_Main;">)</span><span class="msubsup" id="MathJax-Span-172"><span style="display: inline-block; position: relative; width: 1.066em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-173" style="font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.104em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.458em;"><span class="texatom" id="MathJax-Span-174"><span class="mrow" id="MathJax-Span-175"><span style="display: inline-block; position: relative; width: 0.559em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-176" style="font-size: 70.7%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-177" style="font-size: 70.7%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-178" style="font-family: MathJax_Main;">(</span><span class="mi" id="MathJax-Span-179" style="font-family: MathJax_Math-italic;">t</span><span class="mo" id="MathJax-Span-180" style="font-family: MathJax_Main;">)</span><span class="mo" id="MathJax-Span-181" style="font-family: MathJax_Main; padding-left: 0.205em;">+</span><span class="mi" id="MathJax-Span-182" style="font-family: MathJax_Main; padding-left: 0.205em;">Δ</span><span class="msubsup" id="MathJax-Span-183"><span style="display: inline-block; position: relative; width: 1.066em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-184" style="font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.104em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.458em;"><span class="texatom" id="MathJax-Span-185"><span class="mrow" id="MathJax-Span-186"><span style="display: inline-block; position: relative; width: 0.559em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-187" style="font-size: 70.7%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-188" style="font-size: 70.7%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(2.989em, 1007.6em, 4.609em, -999.997em); top: -3.288em; left: 0em;"><span class="mtd" id="MathJax-Span-189"><span class="mrow" id="MathJax-Span-190"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.989em, 1007.6em, 4.609em, -999.997em); top: -3.997em; left: 50%; margin-left: -3.794em;"><span class="mi" id="MathJax-Span-191" style="font-family: MathJax_Main;">Δ</span><span class="msubsup" id="MathJax-Span-192"><span style="display: inline-block; position: relative; width: 1.066em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-193" style="font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.104em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.458em;"><span class="texatom" id="MathJax-Span-194"><span class="mrow" id="MathJax-Span-195"><span style="display: inline-block; position: relative; width: 0.559em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-196" style="font-size: 70.7%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-197" style="font-size: 70.7%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-198" style="font-family: MathJax_Main; padding-left: 0.256em;">=</span><span class="munderover" id="MathJax-Span-199" style="padding-left: 0.256em;"><span style="display: inline-block; position: relative; width: 2.382em; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1001.01em, 4.407em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-200" style="font-family: MathJax_Size1; vertical-align: 0em;">∑</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.546em, 1000.51em, 4.154em, -999.997em); top: -4.452em; left: 1.066em;"><span class="texatom" id="MathJax-Span-201"><span class="mrow" id="MathJax-Span-202"><span style="display: inline-block; position: relative; width: 0.408em; height: 0px;"><span style="position: absolute; clip: rect(3.546em, 1000.41em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-203" style="font-size: 70.7%; font-family: MathJax_Math-italic;">n</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.344em, 1001.37em, 4.154em, -999.997em); top: -3.693em; left: 1.066em;"><span class="texatom" id="MathJax-Span-204"><span class="mrow" id="MathJax-Span-205"><span style="display: inline-block; position: relative; width: 1.268em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1001.22em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-206" style="font-size: 70.7%; font-family: MathJax_Math-italic;">k</span><span class="mo" id="MathJax-Span-207" style="font-size: 70.7%; font-family: MathJax_Main;">=</span><span class="mn" id="MathJax-Span-208" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mi" id="MathJax-Span-209" style="font-family: MathJax_Main; padding-left: 0.154em;">Δ</span><span class="msubsup" id="MathJax-Span-210"><span style="display: inline-block; position: relative; width: 1.066em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-211" style="font-family: MathJax_Math-italic;">τ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.104em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.344em, 1000.46em, 4.154em, -999.997em); top: -4.351em; left: 0.61em;"><span class="texatom" id="MathJax-Span-212"><span class="mrow" id="MathJax-Span-213"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-214" style="font-size: 70.7%; font-family: MathJax_Math-italic;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.394em, 1000.61em, 4.305em, -999.997em); top: -3.693em; left: 0.458em;"><span class="texatom" id="MathJax-Span-215"><span class="mrow" id="MathJax-Span-216"><span style="display: inline-block; position: relative; width: 0.559em; height: 0px;"><span style="position: absolute; clip: rect(3.394em, 1000.51em, 4.305em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-217" style="font-size: 70.7%; font-family: MathJax_Math-italic;">i</span><span class="mi" id="MathJax-Span-218" style="font-size: 70.7%; font-family: MathJax_Math-italic;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.237em; border-left: 0px solid; width: 0px; height: 2.946em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable columnalign="left" rowspacing="4pt" columnspacing="1em"><mtr><mtd><msub><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy="false">(</mo><mi>t</mi><mo>+</mo><mn>1</mn><mo stretchy="false">)</mo><mo>=</mo><mo stretchy="false">(</mo><mn>1</mn><mo>−</mo><mi>ρ</mi><mo stretchy="false">)</mo><msub><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow></msub><mo stretchy="false">(</mo><mi>t</mi><mo stretchy="false">)</mo><mo>+</mo><mi mathvariant="normal">Δ</mi><msub><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow></msub></mtd></mtr><mtr><mtd><mi mathvariant="normal">Δ</mi><msub><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow></msub><mo>=</mo><munderover><mo>∑</mo><mrow class="MJX-TeXAtom-ORD"><mi>k</mi><mo>=</mo><mn>1</mn></mrow><mrow class="MJX-TeXAtom-ORD"><mi>n</mi></mrow></munderover><mi mathvariant="normal">Δ</mi><msubsup><mi>τ</mi><mrow class="MJX-TeXAtom-ORD"><mi>i</mi><mi>j</mi></mrow><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msubsup></mtd></mtr></mtable></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-3">\begin{array}{l} \tau_{i j}(t+1)=(1-\rho) \tau_{i j}(t)+\Delta \tau_{i j} \\ \Delta \tau_{i j}=\sum_{k=1}^{n} \Delta \tau_{i j}^{k} \end{array}</script>\right. 
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.44388em; vertical-align: -0.97194em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">{<!-- --></span></span><span class="mord"><span class="mtable"><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.47194em;"><span class="" style="top: -3.63194em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">t</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mord">1</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mord mathdefault">ρ</span><span class="mclose">)</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault">t</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span><span class="" style="top: -2.42283em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -0.000005em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.804292em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span><span class="mrel mtight">=</span><span class="mord mtight">1</span></span></span></span><span class="" style="top: -3.2029em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">n</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.849108em;"><span class="" style="top: -2.44134em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.394772em;"><span class=""></span></span></span></span></span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.97194em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span></span></span><span class="mclose nulldelimiter"></span></span></span><span class="tag"><span class="strut" style="height: 2.44388em; vertical-align: -0.97194em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">4</span></span><span class="mord">)</span></span></span></span></span></span></span><br> 其中，<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      Δ
     
     
      
       τ
      
      
       
        i
       
       
        j
       
      
      
       k
      
     
    
    
     \Delta \tau_{i j}^{k}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.24388em; vertical-align: -0.394772em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.849108em;"><span class="" style="top: -2.44134em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.394772em;"><span class=""></span></span></span></span></span></span></span></span></span></span>表示第<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      k
     
    
    
     k
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span></span></span></span></span>只蚂蚁在节点<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
    
    
     i
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span>与节点<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      j
     
    
    
     j
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span>连接路径上释放的信息素浓度；<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      Δ
     
     
      
       τ
      
      
       
        i
       
       
        j
       
      
     
    
    
     \Delta \tau_{i j}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.969438em; vertical-align: -0.286108em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>表示所有蚂蚁在节点<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
    
    
     i
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span></span></span></span></span>与节点<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      j
     
    
    
     j
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.85396em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05724em;" class="mord mathdefault">j</span></span></span></span></span>连接路径上释放的信息素浓度之和。</p> </li><li> <p>蚂蚁信息素更新的模型包括蚁周模型（<a href="https://so.csdn.net/so/search?q=Ant&amp;spm=1001.2101.3001.7020" target="_blank" class="hl hl-1" data-report-click="{&quot;spm&quot;:&quot;1001.2101.3001.7020&quot;,&quot;dest&quot;:&quot;https://so.csdn.net/so/search?q=Ant&amp;spm=1001.2101.3001.7020&quot;,&quot;extra&quot;:&quot;{\&quot;searchword\&quot;:\&quot;Ant\&quot;}&quot;}" data-tit="Ant" data-pretit="ant">Ant</a>-Cycle模型）、蚁量模型（Ant-Quantity模型）、蚁密模型（Ant-Density模型）等。</p> <p>区别：</p> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738

蚁周模型利用的是全局信息，即蚂蚁完成一个循环后更新所有路径上的信息素；
蚁量和蚁密模型利用的是局部信息，即蚂蚁完成一步后更新路径上的信息素。

信息素增量不同信息素更新时刻不同信息素更新形式不同

蚁周模型

	信息素增量不同	信息素更新时刻不同	信息素更新形式不同
蚁周模型	信息素增量为 Q / L k Q/L_k </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault">Q</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>,它只与搜索路线有关与具体的路径(i,j)无关</td><td align="center">在第k只蚂蚁完成一次路径搜索后,对线路上所有路径进行信息素的更新</td><td align="center">信息素增量与本次搜索的整体线路有关,因此属于全局信息更新</td></tr><tr><td align="center">蚁量模型</td><td align="center">信息素增量为<span class="katex--inline"><span class="katex"><span class="katex-mathml"> Q / d i j Q/d_{ij} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord mathdefault">Q</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>,与路径(i,j)的长度有关</td><td align="center">在蚁群前进过程中进行，蚂蚁每完成一步移动后更新该路径上的信息素</td><td align="center">利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新</td></tr><tr><td align="center">蚁密模型</td><td align="center">信息素增量为固定值Q</td><td align="center">在蚁群前进过程中进行，蚂蚁每完成一步移动后更新该路径上的信息素</td><td align="center">利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新</td></tr></tbody></table></div><p>蚁周模型的<span class="katex--inline"><span class="katex"><span class="katex-mathml"> Δ τ i j k \Delta \tau_{i j}^{k} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.24388em; vertical-align: -0.394772em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.849108em;"><span class="" style="top: -2.44134em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.394772em;"><span class=""></span></span></span></span></span></span></span></span></span></span>计算公式如下<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml"> Δ τ i j k = { Q / L k ,  第  k  只蚂蚁从城市  i  访问城市  j 0 ,  其他  (5) \tag{5} \Delta \tau_{i j}^{k}= <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-4-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mo>/</mo></mrow><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msub><mo>,</mo></mtd><mtd><mtext>&#xA0;&#x7B2C;&#xA0;</mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">k</mi></mrow><mtext>&#xA0;&#x53EA;&#x8682;&#x8681;&#x4ECE;&#x57CE;&#x5E02;&#xA0;</mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">i</mi></mrow><mtext>&#xA0;&#x8BBF;&#x95EE;&#x57CE;&#x5E02;&#xA0;</mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">j</mi></mrow></mtd></mtr><mtr><mtd><mn>0</mn><mo>,</mo></mtd><mtd><mtext>&#xA0;&#x5176;&#x4ED6;&#xA0;</mtext></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-219" style="width: 100%; display: inline-block; min-width: 13.114em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.382em, 1012.86em, 5.115em, -999.997em); top: -3.997em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-220"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.382em, 1012.86em, 5.115em, -999.997em); top: -3.997em; left: 50%; margin-left: -6.427em;"><span class="mrow" id="MathJax-Span-221"><span class="mo" id="MathJax-Span-222" style="vertical-align: 0em;"><span style="font-family: MathJax_Size3;">{</span></span><span class="mtable" id="MathJax-Span-223" style="padding-right: 0.154em; padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 11.798em; height: 0px;"><span style="position: absolute; clip: rect(2.534em, 1002.63em, 5.014em, -999.997em); top: -3.997em; left: 0em;"><span style="display: inline-block; position: relative; width: 2.686em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.091em, 1002.63em, 4.407em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-224"><span class="mrow" id="MathJax-Span-225"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1002.63em, 4.407em, -999.997em); top: -3.997em; left: 50%; margin-left: -1.364em;"><span class="mi" id="MathJax-Span-226" style="font-family: MathJax_Math-italic;">Q</span><span class="texatom" id="MathJax-Span-227"><span class="mrow" id="MathJax-Span-228"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1000.46em, 4.407em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.251em;"><span class="mo" id="MathJax-Span-229" style="font-family: MathJax_Main;">/</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="msubsup" id="MathJax-Span-230"><span style="display: inline-block; position: relative; width: 1.116em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.66em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-231" style="font-family: MathJax_Math-italic;">L</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.661em;"><span class="texatom" id="MathJax-Span-232"><span class="mrow" id="MathJax-Span-233"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-234" style="font-size: 70.7%; font-family: MathJax_Math-italic;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-235" style="font-family: MathJax_Main;">,</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.192em, 1000.71em, 4.356em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-250"><span class="mrow" id="MathJax-Span-251"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.71em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.402em;"><span class="mn" id="MathJax-Span-252" style="font-family: MathJax_Main;">0</span><span class="mo" id="MathJax-Span-253" style="font-family: MathJax_Main;">,</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(2.483em, 1008.05em, 5.014em, -999.997em); top: -3.997em; left: 3.698em;"><span style="display: inline-block; position: relative; width: 8.102em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.04em, 1008.05em, 4.356em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-236"><span class="mrow" id="MathJax-Span-237"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1008.05em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -4.047em;"><span class="mtext" id="MathJax-Span-238" style="font-family: MathJax_Main;"> <span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">第</span> </span><span class="texatom" id="MathJax-Span-239"><span class="mrow" id="MathJax-Span-240"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-241" style="font-family: MathJax_Main;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="mtext" id="MathJax-Span-242" style="font-family: MathJax_Main;"> <span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">只</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">蚂</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">蚁</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">从</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">城</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">市</span> </span><span class="texatom" id="MathJax-Span-243"><span class="mrow" id="MathJax-Span-244"><span style="display: inline-block; position: relative; width: 0.256em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.26em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-245" style="font-family: MathJax_Main;">i</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="mtext" id="MathJax-Span-246" style="font-family: MathJax_Main;"> <span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">访</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">问</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">城</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">市</span> </span><span class="texatom" id="MathJax-Span-247"><span class="mrow" id="MathJax-Span-248"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.21em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-249" style="font-family: MathJax_Main;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.04em, 1001.27em, 4.356em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-254"><span class="mrow" id="MathJax-Span-255"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1001.27em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.757em;"><span class="mtext" id="MathJax-Span-256" style="font-family: MathJax_Main;"> <span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">其</span><span style="font-family: STIXGeneral, "Arial Unicode MS", serif; font-size: 98%; font-style: normal; font-weight: normal;">他</span> </span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-257"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.03em; border-left: 0px solid; width: 0px; height: 2.533em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mo>/</mo></mrow><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msub><mo>,</mo></mtd><mtd><mtext> 第 </mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">k</mi></mrow><mtext> 只蚂蚁从城市 </mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">i</mi></mrow><mtext> 访问城市 </mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">j</mi></mrow></mtd></mtr><mtr><mtd><mn>0</mn><mo>,</mo></mtd><mtd><mtext> 其他 </mtext></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-4">\begin{cases}Q / L_{k}, & \text { 第 } \mathrm{k} \text { 只蚂蚁从城市 } \mathrm{i} \text { 访问城市 } \mathrm{j} \\ 0, & \text { 其他 }\end{cases}</script> </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28222em; vertical-align: -0.383108em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.899108em;"><span class="" style="top: -2.453em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.383108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 3.00003em; vertical-align: -1.25003em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size4">{<!-- --></span></span><span class="mord"><span class="mtable"><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord mathdefault">Q</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">0</span><span class="mpunct">,</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 1em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord"> </span><span class="mord cjk_fallback">第</span><span class="mord"> </span></span><span class="mord"><span class="mord mathrm">k</span></span><span class="mord text"><span class="mord"> </span><span class="mord cjk_fallback">只蚂蚁从城市</span><span class="mord"> </span></span><span class="mord"><span class="mord mathrm">i</span></span><span class="mord text"><span class="mord"> </span><span class="mord cjk_fallback">访问城市</span><span class="mord"> </span></span><span class="mord"><span class="mord mathrm">j</span></span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord"> </span><span class="mord cjk_fallback">其他</span><span class="mord"> </span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span><span class="tag"><span class="strut" style="height: 3.00003em; vertical-align: -1.25003em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">5</span></span><span class="mord">)</span></span></span></span></span></span></span><br> 式中<span class="katex--inline"><span class="katex"><span class="katex-mathml"> Q Q </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">Q</span></span></span></span></span>为信息素常数（一个正的常数），表示蚂蚁循环一次所释放的信息素总量。<span class="katex--inline"><span class="katex"><span class="katex-mathml"> L k L_{k} </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.83333em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>为第k只蚂蚁经过路径的总长度。</p> </li></ul> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225

信息素增量为

         Q
        
        
         /
        
        
         
          L
         
         
          k
         
        
       
       
        Q/L_k
       
      
     </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault">Q</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>,它只与搜索路线有关与具体的路径(i,j)无关</td><td align="center">在第k只蚂蚁完成一次路径搜索后,对线路上所有路径进行信息素的更新</td><td align="center">信息素增量与本次搜索的整体线路有关,因此属于全局信息更新</td></tr><tr><td align="center">蚁量模型</td><td align="center">信息素增量为<span class="katex--inline"><span class="katex"><span class="katex-mathml">
     
      
       
        
         Q
        
        
         /
        
        
         
          d
         
         
          
           i
          
          
           j
          
         
        
       
       
        Q/d_{ij}
       
      
     </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.03611em; vertical-align: -0.286108em;"></span><span class="mord mathdefault">Q</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">d</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.311664em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.286108em;"><span class=""></span></span></span></span></span></span></span></span></span></span>,与路径(i,j)的长度有关</td><td align="center">在蚁群前进过程中进行，蚂蚁每完成一步移动后更新该路径上的信息素</td><td align="center">利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新</td></tr><tr><td align="center">蚁密模型</td><td align="center">信息素增量为固定值Q</td><td align="center">在蚁群前进过程中进行，蚂蚁每完成一步移动后更新该路径上的信息素</td><td align="center">利用蚂蚁所走路径上的信息进行更新,因此属于局部信息更新</td></tr></tbody></table></div><p>蚁周模型的<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      Δ
     
     
      
       τ
      
      
       
        i
       
       
        j
       
      
      
       k
      
     
    
    
     \Delta \tau_{i j}^{k}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.24388em; vertical-align: -0.394772em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.849108em;"><span class="" style="top: -2.44134em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.394772em;"><span class=""></span></span></span></span></span></span></span></span></span></span>计算公式如下<br> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
   
    
     
      
       
       
        
         
          Δ
         
         
          
           τ
          
          
           
            i
           
           
            j
           
          
          
           k
          
         
         
          =
         
         
          
           {
          
          
           
            
             
              
               
                Q
               
               
                /
               
               
                
                 L
                
                
                 k
                
               
               
                ,
               
              
             
            
            
             
              
               
                &nbsp;第&nbsp;
               
               
                k
               
               
                &nbsp;只蚂蚁从城市&nbsp;
               
               
                i
               
               
                &nbsp;访问城市&nbsp;
               
               
                j
               
              
             
            
           
           
            
             
              
               
                0
               
               
                ,
               
              
             
            
            
             
              
               &nbsp;其他&nbsp;
              
             
            
           
          
         
        
       
       
       
        
         (5)
        
       
      
     
     
       \tag{5} \Delta \tau_{i j}^{k}= <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-4-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mrow><mo>{</mo><mtable columnalign=&quot;left left&quot; rowspacing=&quot;.2em&quot; columnspacing=&quot;1em&quot; displaystyle=&quot;false&quot;><mtr><mtd><mi>Q</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>/</mo></mrow><msub><mi>L</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi>k</mi></mrow></msub><mo>,</mo></mtd><mtd><mtext>&amp;#xA0;&amp;#x7B2C;&amp;#xA0;</mtext><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi mathvariant=&quot;normal&quot;>k</mi></mrow><mtext>&amp;#xA0;&amp;#x53EA;&amp;#x8682;&amp;#x8681;&amp;#x4ECE;&amp;#x57CE;&amp;#x5E02;&amp;#xA0;</mtext><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi mathvariant=&quot;normal&quot;>i</mi></mrow><mtext>&amp;#xA0;&amp;#x8BBF;&amp;#x95EE;&amp;#x57CE;&amp;#x5E02;&amp;#xA0;</mtext><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mi mathvariant=&quot;normal&quot;>j</mi></mrow></mtd></mtr><mtr><mtd><mn>0</mn><mo>,</mo></mtd><mtd><mtext>&amp;#xA0;&amp;#x5176;&amp;#x4ED6;&amp;#xA0;</mtext></mtd></mtr></mtable><mo fence=&quot;true&quot; stretchy=&quot;true&quot; symmetric=&quot;true&quot;></mo></mrow></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-219" style="width: 100%; display: inline-block; min-width: 13.114em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.382em, 1012.86em, 5.115em, -999.997em); top: -3.997em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-220"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.382em, 1012.86em, 5.115em, -999.997em); top: -3.997em; left: 50%; margin-left: -6.427em;"><span class="mrow" id="MathJax-Span-221"><span class="mo" id="MathJax-Span-222" style="vertical-align: 0em;"><span style="font-family: MathJax_Size3;">{</span></span><span class="mtable" id="MathJax-Span-223" style="padding-right: 0.154em; padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 11.798em; height: 0px;"><span style="position: absolute; clip: rect(2.534em, 1002.63em, 5.014em, -999.997em); top: -3.997em; left: 0em;"><span style="display: inline-block; position: relative; width: 2.686em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.091em, 1002.63em, 4.407em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-224"><span class="mrow" id="MathJax-Span-225"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1002.63em, 4.407em, -999.997em); top: -3.997em; left: 50%; margin-left: -1.364em;"><span class="mi" id="MathJax-Span-226" style="font-family: MathJax_Math-italic;">Q</span><span class="texatom" id="MathJax-Span-227"><span class="mrow" id="MathJax-Span-228"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1000.46em, 4.407em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.251em;"><span class="mo" id="MathJax-Span-229" style="font-family: MathJax_Main;">/</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="msubsup" id="MathJax-Span-230"><span style="display: inline-block; position: relative; width: 1.116em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.66em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-231" style="font-family: MathJax_Math-italic;">L</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -3.845em; left: 0.661em;"><span class="texatom" id="MathJax-Span-232"><span class="mrow" id="MathJax-Span-233"><span style="display: inline-block; position: relative; width: 0.357em; height: 0px;"><span style="position: absolute; clip: rect(3.344em, 1000.36em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-234" style="font-size: 70.7%; font-family: MathJax_Math-italic;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-235" style="font-family: MathJax_Main;">,</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.192em, 1000.71em, 4.356em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-250"><span class="mrow" id="MathJax-Span-251"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.71em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.402em;"><span class="mn" id="MathJax-Span-252" style="font-family: MathJax_Main;">0</span><span class="mo" id="MathJax-Span-253" style="font-family: MathJax_Main;">,</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(2.483em, 1008.05em, 5.014em, -999.997em); top: -3.997em; left: 3.698em;"><span style="display: inline-block; position: relative; width: 8.102em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.04em, 1008.05em, 4.356em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-236"><span class="mrow" id="MathJax-Span-237"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1008.05em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -4.047em;"><span class="mtext" id="MathJax-Span-238" style="font-family: MathJax_Main;">&nbsp;<span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">第</span>&nbsp;</span><span class="texatom" id="MathJax-Span-239"><span class="mrow" id="MathJax-Span-240"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-241" style="font-family: MathJax_Main;">k</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="mtext" id="MathJax-Span-242" style="font-family: MathJax_Main;">&nbsp;<span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">只</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">蚂</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">蚁</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">从</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">城</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">市</span>&nbsp;</span><span class="texatom" id="MathJax-Span-243"><span class="mrow" id="MathJax-Span-244"><span style="display: inline-block; position: relative; width: 0.256em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.26em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-245" style="font-family: MathJax_Main;">i</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="mtext" id="MathJax-Span-246" style="font-family: MathJax_Main;">&nbsp;<span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">访</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">问</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">城</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">市</span>&nbsp;</span><span class="texatom" id="MathJax-Span-247"><span class="mrow" id="MathJax-Span-248"><span style="display: inline-block; position: relative; width: 0.306em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.21em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-249" style="font-family: MathJax_Main;">j</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.04em, 1001.27em, 4.356em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-254"><span class="mrow" id="MathJax-Span-255"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1001.27em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.757em;"><span class="mtext" id="MathJax-Span-256" style="font-family: MathJax_Main;">&nbsp;<span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">其</span><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">他</span>&nbsp;</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-257"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.03em; border-left: 0px solid; width: 0px; height: 2.533em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mi>Q</mi><mrow class="MJX-TeXAtom-ORD"><mo>/</mo></mrow><msub><mi>L</mi><mrow class="MJX-TeXAtom-ORD"><mi>k</mi></mrow></msub><mo>,</mo></mtd><mtd><mtext>&nbsp;第&nbsp;</mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">k</mi></mrow><mtext>&nbsp;只蚂蚁从城市&nbsp;</mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">i</mi></mrow><mtext>&nbsp;访问城市&nbsp;</mtext><mrow class="MJX-TeXAtom-ORD"><mi mathvariant="normal">j</mi></mrow></mtd></mtr><mtr><mtd><mn>0</mn><mo>,</mo></mtd><mtd><mtext>&nbsp;其他&nbsp;</mtext></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-4">\begin{cases}Q / L_{k}, & \text { 第 } \mathrm{k} \text { 只蚂蚁从城市 } \mathrm{i} \text { 访问城市 } \mathrm{j} \\ 0, & \text { 其他 }\end{cases}</script> 
     
    
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28222em; vertical-align: -0.383108em;"></span><span class="mord">Δ</span><span class="mord"><span style="margin-right: 0.1132em;" class="mord mathdefault">τ</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.899108em;"><span class="" style="top: -2.453em; margin-left: -0.1132em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span style="margin-right: 0.05724em;" class="mord mathdefault mtight">j</span></span></span></span><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.383108em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 3.00003em; vertical-align: -1.25003em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size4">{<!-- --></span></span><span class="mord"><span class="mtable"><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord mathdefault">Q</span><span class="mord">/</span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mpunct">,</span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">0</span><span class="mpunct">,</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 1em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">&nbsp;</span><span class="mord cjk_fallback">第</span><span class="mord">&nbsp;</span></span><span class="mord"><span class="mord mathrm">k</span></span><span class="mord text"><span class="mord">&nbsp;</span><span class="mord cjk_fallback">只蚂蚁从城市</span><span class="mord">&nbsp;</span></span><span class="mord"><span class="mord mathrm">i</span></span><span class="mord text"><span class="mord">&nbsp;</span><span class="mord cjk_fallback">访问城市</span><span class="mord">&nbsp;</span></span><span class="mord"><span class="mord mathrm">j</span></span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">&nbsp;</span><span class="mord cjk_fallback">其他</span><span class="mord">&nbsp;</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span><span class="tag"><span class="strut" style="height: 3.00003em; vertical-align: -1.25003em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">5</span></span><span class="mord">)</span></span></span></span></span></span></span><br> 式中<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      Q
     
    
    
     Q
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">Q</span></span></span></span></span>为信息素常数（一个正的常数），表示蚂蚁循环一次所释放的信息素总量。<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       L
      
      
       k
      
     
    
    
     L_{k}
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.83333em; vertical-align: -0.15em;"></span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span></span></span></span></span>为第k只蚂蚁经过路径的总长度。</p> </li></ul> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225

4. 算法步骤

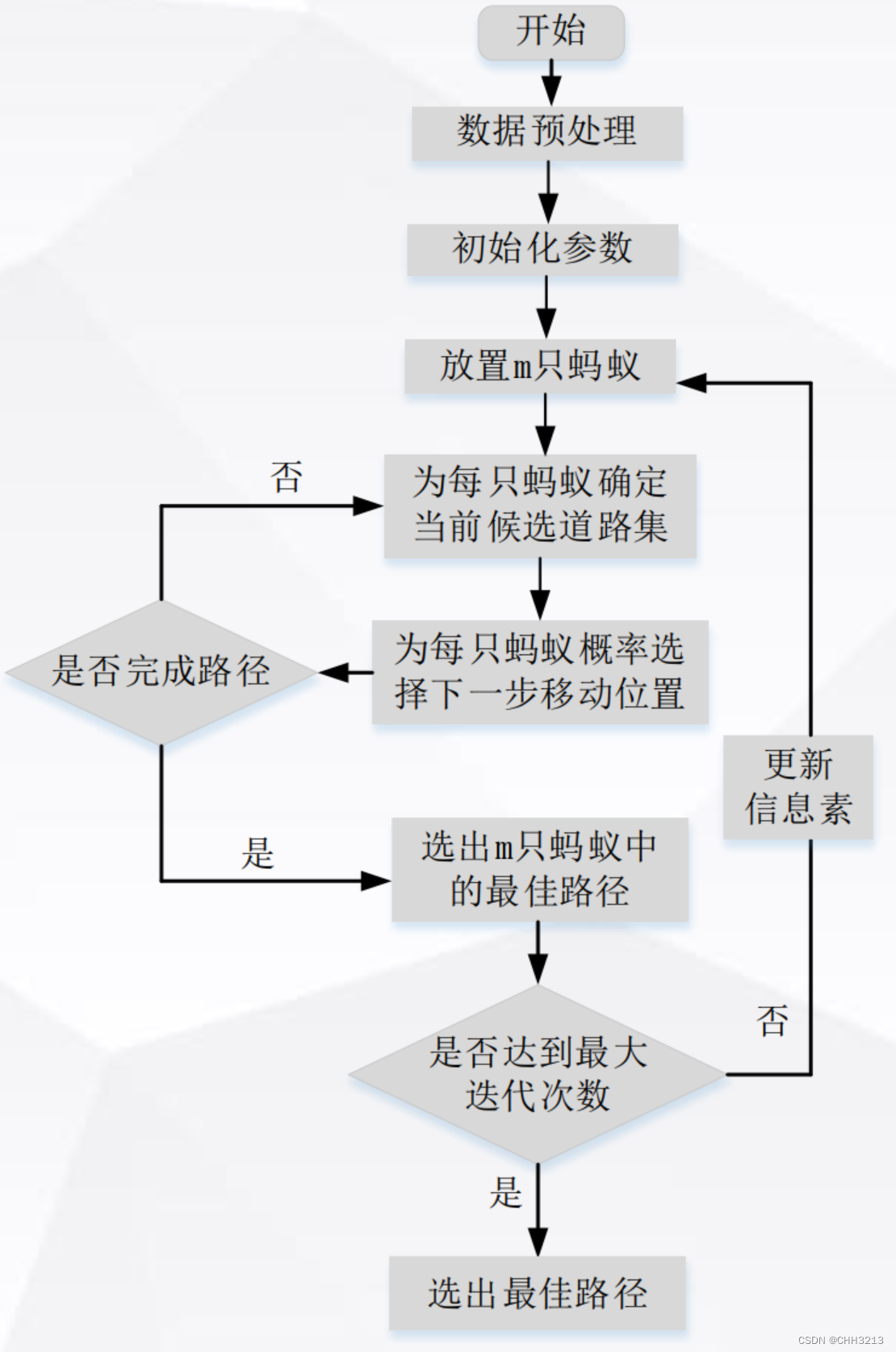
对相关参数进行初始化，如蚁群规模（蚂蚁数量）

      m
     
    
    
     m
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span class="mord mathdefault">m</span></span></span></span></span>、信息素重要程度因子<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      α
     
    
    
     \alpha
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.43056em; vertical-align: 0em;"></span><span style="margin-right: 0.0037em;" class="mord mathdefault">α</span></span></span></span></span>、启发函数重要程度因子<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      β
     
    
    
     \beta
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.88888em; vertical-align: -0.19444em;"></span><span style="margin-right: 0.05278em;" class="mord mathdefault">β</span></span></span></span></span>、信息素挥发因子<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      ρ
     
    
    
     \rho
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.625em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">ρ</span></span></span></span></span>、信息素常数<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      Q
     
    
    
     Q
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.87777em; vertical-align: -0.19444em;"></span><span class="mord mathdefault">Q</span></span></span></span></span>、最大迭代次数<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
     
      t
     
     
      e
     
     
      r
     
     
      m
     
     
      a
     
     
      x
     
    
    
     itermax
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span><span class="mord mathdefault">t</span><span class="mord mathdefault">e</span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mord mathdefault">m</span><span class="mord mathdefault">a</span><span class="mord mathdefault">x</span></span></span></span></span>。</p> </li><li> <p>构建解空间，将各个蚂蚁随机地置于不同的出发点，为每只蚂蚁确定当前候选道路集</p> </li><li> <p>更新信息素计算每个蚂蚁经过路径长度<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      
       L
      
      
       k
      
     
     
      (
     
     
      k
     
     
      =
     
     
      1
     
     
      ,
     
     
      2
     
     
      ,
     
     
      …
     
     
      ，
     
     
      m
     
     
      )
     
    
    
     L_k(k=1,2,…，m)
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathdefault">L</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.336108em;"><span class="" style="top: -2.55em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span style="margin-right: 0.03148em;" class="mord mathdefault mtight">k</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span style="margin-right: 0.03148em;" class="mord mathdefault">k</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="minner">…</span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord cjk_fallback">，</span><span class="mord mathdefault">m</span><span class="mclose">)</span></span></span></span></span>，记录当前迭代次数中的最优解（最短路径）。同时，对各个节点连接路径上信息素浓度进行更新。</p> </li><li> <p>判断是否终止若<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
     
      t
     
     
      e
     
     
      r
     
     
      &lt;
     
     
      i
     
     
      t
     
     
      e
     
     
      r
     
     
      m
     
     
      a
     
     
      x
     
    
    
     iter&lt;itermax
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69862em; vertical-align: -0.0391em;"></span><span class="mord mathdefault">i</span><span class="mord mathdefault">t</span><span class="mord mathdefault">e</span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">&lt;</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span><span class="mord mathdefault">t</span><span class="mord mathdefault">e</span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mord mathdefault">m</span><span class="mord mathdefault">a</span><span class="mord mathdefault">x</span></span></span></span></span>，则令<span class="katex--inline"><span class="katex"><span class="katex-mathml">
  
   
    
     
      i
     
     
      t
     
     
      e
     
     
      r
     
     
      =
     
     
      i
     
     
      t
     
     
      e
     
     
      r
     
     
      +
     
     
      1
     
    
    
     iter=iter+1
    
   
  </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.65952em; vertical-align: 0em;"></span><span class="mord mathdefault">i</span><span class="mord mathdefault">t</span><span class="mord mathdefault">e</span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mspace" style="margin-right: 0.277778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.277778em;"></span></span><span class="base"><span class="strut" style="height: 0.74285em; vertical-align: -0.08333em;"></span><span class="mord mathdefault">i</span><span class="mord mathdefault">t</span><span class="mord mathdefault">e</span><span style="margin-right: 0.02778em;" class="mord mathdefault">r</span><span class="mspace" style="margin-right: 0.222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.222222em;"></span></span><span class="base"><span class="strut" style="height: 0.64444em; vertical-align: 0em;"></span><span class="mord">1</span></span></span></span></span>，清空蚂蚁经过路径的记录表，并返回步骤2；否则，终止计算，输出最优解。</p> </li></ol> 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223

5. python实现

使用蚁群算法解决旅行商问题（TSP），代码来自博客。

import numpy as np
import matplotlib.pyplot as plt
1
2

# 城市坐标(52个城市)
coordinates = np.array([[565.0,575.0],[25.0,185.0],[345.0,750.0],[945.0,685.0],[845.0,655.0],
[880.0,660.0],[25.0,230.0],[525.0,1000.0],[580.0,1175.0],[650.0,1130.0],
[1605.0,620.0],[1220.0,580.0],[1465.0,200.0],[1530.0, 5.0],[845.0,680.0],
[725.0,370.0],[145.0,665.0],[415.0,635.0],[510.0,875.0],[560.0,365.0],
[300.0,465.0],[520.0,585.0],[480.0,415.0],[835.0,625.0],[975.0,580.0],
[1215.0,245.0],[1320.0,315.0],[1250.0,400.0],[660.0,180.0],[410.0,250.0],
[420.0,555.0],[575.0,665.0],[1150.0,1160.0],[700.0,580.0],[685.0,595.0],
[685.0,610.0],[770.0,610.0],[795.0,645.0],[720.0,635.0],[760.0,650.0],
[475.0,960.0],[95.0,260.0],[875.0,920.0],[700.0,500.0],[555.0,815.0],
[830.0,485.0],[1170.0, 65.0],[830.0,610.0],[605.0,625.0],[595.0,360.0],
[1340.0,725.0],[1740.0,245.0]])

def getdistmat(coordinates):
num = coordinates.shape[0]
distmat = np.zeros((52, 52))
for i in range(num):
for j in range(i, num):
distmat[i][j] = distmat[j][i] = np.linalg.norm(
coordinates[i] - coordinates[j])
return distmat

# #//初始化
distmat = getdistmat(coordinates)
numant = 45 ##// 蚂蚁个数
numcity = coordinates.shape[0] ##// 城市个数
alpha = 1 ##// 信息素重要程度因子
beta = 5 ##// 启发函数重要程度因子
rho = 0.1 ##// 信息素的挥发速度
Q = 1 ##//信息素释放总量
iter = 0##//循环次数
itermax = 200#//循环最大值
etatable = 1.0 / (distmat + np.diag([1e10] numcity)) #// 启发函数矩阵，表示蚂蚁从城市i转移到矩阵j的期望程度
pheromonetable = np.ones((numcity, numcity)) #// 信息素矩阵
pathtable = np.zeros((numant, numcity)).astype(int) #// 路径记录表
distmat = getdistmat(coordinates) #// 城市的距离矩阵
lengthaver = np.zeros(itermax) #// 各代路径的平均长度
lengthbest = np.zeros(itermax) #// 各代及其之前遇到的最佳路径长度
pathbest = np.zeros((itermax, numcity)) #// 各代及其之前遇到的最佳路径长度
#//核心点-循环迭代
while iter < itermax:
#// 随机产生各个蚂蚁的起点城市
if numant <= numcity:
#// 城市数比蚂蚁数多
pathtable[:, 0] = np.random.permutation(range(0, numcity))[:numant]
else:
#// 蚂蚁数比城市数多，需要补足
pathtable[:numcity, 0] = np.random.permutation(range(0, numcity))[:]
pathtable[numcity:, 0] = np.random.permutation(range(0, numcity))[
:numant - numcity]
length = np.zeros(numant) # 计算各个蚂蚁的路径距离
for i in range(numant):
visiting = pathtable[i, 0] # 当前所在的城市
unvisited = set(range(numcity)) # 未访问的城市,以集合的形式存储{}
unvisited.remove(visiting) # 删除元素；利用集合的remove方法删除存储的数据内容
for j in range(1, numcity): # 循环numcity-1次，访问剩余的numcity-1个城市
# 每次用轮盘法选择下一个要访问的城市
listunvisited = list(unvisited)
probtrans = np.zeros(len(listunvisited))
for k in range(len(listunvisited)):
probtrans[k] = np.power(pheromonetable[visiting][listunvisited[k]], alpha)
np.power(etatable[visiting][listunvisited[k]], beta)
cumsumprobtrans = (probtrans / sum(probtrans)).cumsum()
cumsumprobtrans -= np.random.rand()
k = listunvisited[(np.where(cumsumprobtrans > 0)[0])[0]]
# 元素的提取（也就是下一轮选的城市）
pathtable[i, j] = k # 添加到路径表中（也就是蚂蚁走过的路径)
unvisited.remove(k) # 然后在为访问城市set中remove（）删除掉该城市
length[i] += distmat[visiting][k]
visiting = k
# 蚂蚁的路径距离包括最后一个城市和第一个城市的距离
length[i] += distmat[visiting][pathtable[i, 0]]
# 包含所有蚂蚁的一个迭代结束后，统计本次迭代的若干统计参数
lengthaver[iter] = length.mean()
if iter 0:
lengthbest[iter] = length.min()
pathbest[iter] = pathtable[length.argmin()].copy()
else:
if length.min() > lengthbest[iter - 1]:
lengthbest[iter] = lengthbest[iter - 1]
pathbest[iter] = pathbest[iter - 1].copy()
else:
lengthbest[iter] = length.min()
pathbest[iter] = pathtable[length.argmin()].copy()
# 更新信息素
changepheromonetable = np.zeros((numcity, numcity))
for i in range(numant):
for j in range(numcity - 1):
changepheromonetable[pathtable[i, j]][pathtable[i, j + 1]] += Q / distmat[pathtable[i, j]][
pathtable[i, j + 1]] # 计算信息素增量
changepheromonetable[pathtable[i, j + 1]][pathtable[i, 0]] += Q / distmat[pathtable[i, j + 1]][pathtable[i, 0]]
pheromonetable = (1 - rho) * pheromonetable +
changepheromonetable # 计算信息素公式
if iter%300:
print(“iter(迭代次数):”, iter)
iter += 1 # 迭代次数指示器+1

# 做出平均路径长度和最优路径长度
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(12, 10))
axes[0].plot(lengthaver, ‘k’, marker=u’‘)
axes[0].set_title(‘Average Length’)
axes[0].set_xlabel(u’iteration’)

axes[1].plot(lengthbest, ‘k’, marker=u’‘)
axes[1].set_title(‘Best Length’)
axes[1].set_xlabel(u’iteration’)
fig.savefig(‘average_best.png’, dpi=500, bbox_inches=‘tight’)
plt.show()

# 作出找到的最优路径图
bestpath = pathbest[-1]
plt.plot(coordinates[:, 0], coordinates[:, 1], ‘r.’, marker=u’ $\cdot$ ’)
plt.xlim([-100, 2000])
plt.ylim([-100, 1500])

for i in range(numcity - 1):
m = int(bestpath[i])
n = int(bestpath[i + 1])
plt.plot([coordinates[m][0], coordinates[n][0]], [
coordinates[m][1], coordinates[n][1]], ‘k’)
plt.plot([coordinates[int(bestpath[0])][0], coordinates[int(n)][0]],
[coordinates[int(bestpath[0])][1], coordinates[int(n)][1]], ‘b’)
ax = plt.gca()
ax.set_title(“Best Path”)
ax.set_xlabel(‘X axis’)
ax.set_ylabel(‘Y_axis’)

plt.savefig(‘best path.png’, dpi=500, bbox_inches=‘tight’)
plt.show()

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/很楠不爱3/article/detail/470980