Robust and Efficient Quadrotor TrajectoryGeneration for Fast Autonomous Flight快速自主飞行的鲁棒高效四旋翼轨迹生成_robust and efficient quadrotor trajectory generati

快速自主飞行的鲁棒高效四旋翼轨迹生成

摘要

在这封信中，我们提出了一种用于三维复杂环境中快速飞行的鲁棒高效的四旋翼运动规划系统。我们采用动态路径搜索方法，在离散控制空间中找到安全、动态可行和最小时间的初始轨迹。我们通过B样条优化提高了轨迹的平滑度和间隙，该优化结合了欧几里德距离场的梯度信息和动态约束，有效地利用了B样条的凸包特性。最后，通过将最终轨迹表示为非均匀B样条，采用迭代时间调整方法来保证动态可行和非保守轨迹。我们在各种复杂的模拟环境中验证了我们提出的方法。该方法的能力也在具有挑战性的现实世界任务中得到验证。我们将代码作为开源包发布。1索引术语运动和路径规划，空中系统：感知和自主，避免碰撞。

I、介绍

无人机（UAV）最近参与了越来越多的应用，例如工业检查、搜索和救援以及包裹递送。为了在这些场景中实现完全自主，运动规划模块在生成安全平稳的运动方面起着至关重要的作用。

尽管已经提出了大量关于四旋翼轨迹生成的工作，但仍有两个关键的未解决问题。首先，考虑到有限的时间和机载计算资源，现有的工作无法保证以高成功率生成安全和动态的可行轨迹。然而，轨迹生成的效率和鲁棒性至关重要。在许多情况下，例如在未知环境中高速飞行的四旋翼机，应该在极短的时间内不断地重新生成轨迹，以避免出现紧急威胁。其次，为了确保所生成运动的运动学可行性，通常保守地执行速度和加速度约束。结果，生成的轨迹的攻击性通常很难被调整以满足高飞行速度是优选的应用。

在这封信中，我们提出了一种完整而稳健的在线轨迹生成方法，以系统地解决这两个问题。采用基于启发式搜索和线性二次最小时间控制的动态路径搜索。它在离散控制空间中有效地搜索安全、可行和最小时间的初始路径。然后在精心设计的B样条优化中细化初始路径，该优化利用B样条的凸包特性来结合梯度信息和动态约束。它改进了初始路径，并快速收敛到平滑、安全和动态可行的轨迹。最后，将轨迹表示为非均匀B样条，我们研究了导数控制点与时间分配之间的关系。基于这些关系，采用迭代时间调整方法，从剖面中挤出不可行的速度和加速度，同时避免对其进行保守约束。

与现有工作相比，我们提出的方法能够在更短的时间内在杂乱的环境中生成高质量的轨迹，并且成功率更高。它可以在动态可行的前提下产生攻击性运动。我们在许多模拟复杂环境中展示了我们方法的效率和鲁棒性。我们还证明，我们的方法即使在挑战快速飞行时也能胜任，因为真实世界的实验应该在很短的时间内重复生成轨迹。我们的贡献总结如下：

        1）我们提出了一种鲁棒、高效的系统方法，该方法结合了动态路径搜索、B样条优化和时间调整，其中安全性、动态可行性和攻击性是自下而上构建的。

        2）我们提出了一种基于B样条曲线凸包特性的优化公式，该公式巧妙地结合了梯度信息和动态约束，快速收敛以生成平滑、安全和动态可行的轨迹。

        3）我们研究了导数控制点与非均匀B样条时间分配之间的关系。应用基于关系的时间调整方法来保证可行和非保守运动。

        4）我们对我们提出的方法进行了广泛的模拟和真实世界评估。源代码作为ros包发布。

II、相关工作

A、硬约束方法

最近的一些工作已经解决了轨迹生成的问题。硬约束方法的先驱是最小捕捉轨迹生成[1]，其中轨迹表示为分段多项式，并通过求解二次规划（QP）问题生成。[2] 表明可以以闭合形式获得最小捕捉轨迹，其中通过迭代添加中间航路点来确保轨迹的安全性。Works[3]–[7]在两步流水线中生成轨迹。首先提取由立方体[3]、[8]、球体[4]、[9]或多面体[5]的序列表示的自由空间，然后进行凸优化，在可行空间内生成平滑轨迹。[6] ，[7]提出了一种基于B样条的运动动力学搜索，以找到初始轨迹，然后通过弹性带优化方法对初始轨迹进行细化。

均匀B样条的使用确保了动态可行性，但可能产生保守运动。这些方法的一个常见缺点是，轨迹的时间分配是由天真的启发式给出的。然而，选择不当的时间分配会显著降低轨迹的质量。此外，只有通过迭代添加更多约束并解决二次规划问题才能获得可行的解决方案，这对于实时应用来说是不可取的。为了解决这些问题，[8]提出了一种方法来搜索具有良好分配时间的路径，并通过优化来保证轨迹的安全性和动力学可行性。硬约束方法通过凸公式确保全局最优。然而，自由空间中障碍物的距离被忽略，这通常导致轨迹接近障碍物。此外，运动动力学约束是保守的，使得弹道的速度不适合快速飞行。

B、软约束方法

还有一些方法将轨迹生成公式化为考虑平滑性和安全性的非线性优化问题。[10] 通过使用梯度下降方法最小化其平滑度和碰撞成本来生成离散时间轨迹。[11] 具有类似的问题公式，但优化是通过无梯度采样方法解决的。[12] 将它们扩展到连续时间多项式轨迹。由于时间参数化是连续的，它避免了数值微分误差，并且更准确地表示四旋翼的运动。然而，它的成功率很低。为了解决这个问题，[13]首先使用基于通知采样的路径搜索方法来找到无冲突的初始路径。该路径用作非线性优化的更高质量的初始猜测，从而提高了成功率。在[14]中，轨迹被参数化为均匀B样条。由于B样条曲线本质上是连续的，因此不需要显式地强制连续性，这减少了约束的数量。由于其局部性，它对于局部重新规划也特别有用。软约束方法利用梯度信息将轨迹推离障碍物，但存在局部极小值，并且不能很好地保证成功率和运动学可行性。我们的优化方法还利用梯度信息来提高轨迹的安全性。然而，与以前计算沿轨迹的昂贵线积分的方法不同，基于B样条曲线的凸包特性，公式被重新设计为更简单。它大大提高了计算效率和收敛速度。

|||、运动动力学路径搜索

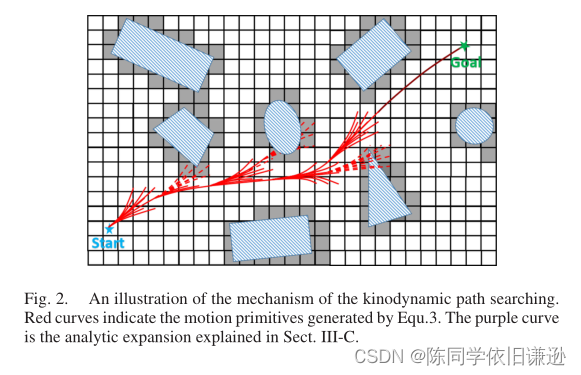
我们的前端运动动力学路径搜索模块源自首次为自动驾驶汽车提出的混合状态A*搜索[15]。它在体素网格图中搜索安全且动态可行的轨迹，该轨迹在持续时间和控制成本方面是最小的。如算法1和图2所示，搜索循环类似于标准A*算法，其中P和C表示开集和闭集。与直线不同，与四旋翼动力学相关的运动图元被用作图形边缘。结构节点用于记录基元、基元结束的体素以及gc和fc成本（第III-B节）。基本体迭代地展开（）体素栅格贴图，并修剪除具有最小fc的体素之外的同一体素中的那些（删减（））。然后CheckFeasible（）检查剩余原语的安全性和动态可行性。这个过程一直持续到任何原始的达成目标或AnalyticExpand（）（第III-C节）成功为止。

 A、基元生成

我们首先讨论Expand（）中使用的运动原语的生成。四旋翼系统的差分平坦度允许我们通过三个独立的一维时间参数化多项式函数来表示轨迹[1]：

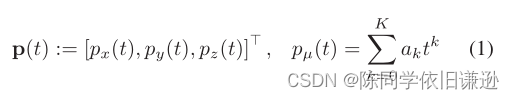
 其中μ∈ {x，y，z}。从四旋翼系统的角度来看，它对应于线性时不变（LTI）系统。设x（t）：=[p（t）？，˙p（t），…，p（n−1） （t）？]？∈ 十、⊂ R3n是状态向量。设u（t）：=p（n）（t）∈ U：=[−umax，umax]3⊂ R3是控制输入。状态空间模型可以定义为：

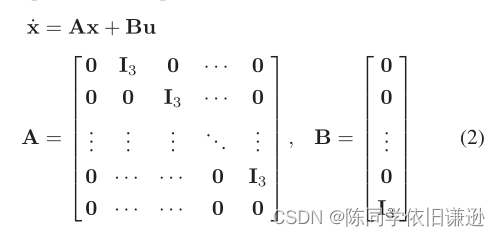
状态方程的完整解表示为：

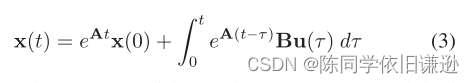
 其给出了初始状态为x（0）且控制输入为u（t）的四旋翼系统的轨迹。

在Expand（）中，给定四旋翼的当前状态，一组离散化控制输入UD⊂ U适用于持续时间τ。在实践中，我们选择n=2，这对应于一个双积分器。每个轴[−umax，umax]统一离散为{−umax，− r−1最大值，…，r−1r umax，umax}，这导致（2r+1）3个原语。

B、实际成本和启发式成本

当我们的目标是找到时间和控制成本最优的轨迹时，我们将轨迹的成本定义为：

 根据此定义，EdgeCost（）计算使用离散化输入u（t）=ud和持续时间τ生成的运动原语的成本，即ec=（？ud？2+ρ）τ。

遵循A*的术语，我们使用gc表示从开始状态xs到当前状态xc的最佳路径的实际成本。假设此最佳路径由J个原语组成，gc计算为：gc=？J J=1（？udj？2+ρ）τ。

如A*所示，一种可接受的、信息丰富的启发式方法对于加快搜索速度至关重要。因此，我们还设计了一个启发式（）。通过应用Pontryagins最小原理[16]，我们计算了从xc到目标状态xg的J（T）最小化的闭合形式轨迹：

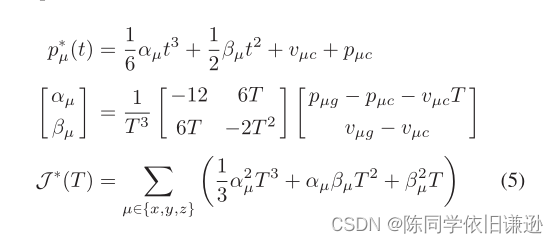
 其中pμc、vμc、pμg、vμg是当前和目标位置和速度。J∗（T）是由等式4定义的成本。为了找到使成本最小化的最佳时间T，我们将αμ，βμ代入J∗（T）并找到∂J∗（吨）∂T=0.最小成本最小的根∗ 并且选择可行的轨迹并表示为Th.W e u s e J∗（Th）作为启发式hc。最后，fc定义为：fc=gc+hc=gc+J∗（Th）。

C、分析扩展

由于离散化的控制输入，很难使原始末端精确地处于目标状态。为了补偿它并加快搜索速度，我们引入了一个解析展开方案。当节点从开放集弹出时，使用第节中的相同方法计算从xc到xg的轨迹。III-B。如果它通过了安全性和动态可行性检查，则提前终止搜索。该策略对于提高效率非常有效，尤其是在稀疏环境中，因为它具有更高的成功率并提前终止搜索。

D、最优性和完备性

理论上，我们不能保证路径搜索的最优性和完整性。然而，实际性能令人满意。对于最优性，评估（第VII-A1节）表明，最优性的牺牲是可接受和可调整的。此外，如果初始路径接近最佳值，我们的优化（第四节）将找到最佳值。对于完整性，评估（第VII-A1节）表明，在实践中，它可以在大多数情况下找到可行的解决方案。此外，我们的方法可以扩展到支持可变持续时间原语和可变分辨率体素网格，如[15]所述，以提供更强的完整性保证。

VI、B样条轨迹优化

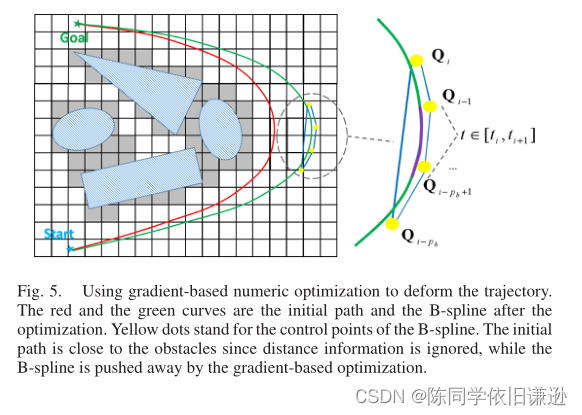
如第III-D。由路径搜索产生的路径可能是次优的。此外，由于忽略了自由空间中的距离信息，该路径通常接近障碍物（图5）。因此，我们在所提出的B样条优化中提高了路径的平滑度和间隙。利用均匀B样条的凸包特性，结合欧几里德距离场和动态约束的梯度信息，在很短的时间内收敛，生成平滑、安全和动态可行的轨迹。

 A、均匀B样条

B样条是一个分段多项式，由其阶数pb、N+1个控制点{Q0，Q1，…，QN}和节点向量[t0，t1，…，tM]唯一确定，其中Qi∈ R3，tm∈ R和M=N+pb+1。B样条轨迹由时间t参数化，其中t∈ [tpb，tM−pb]。对于均匀B样条曲线，每个节点跨度Δtm=tm+1− tm具有相同的Δt值。评估时间T的位置∈ [tm，tm+1）⊂ [tpb，tM−pb]，我们首先将t归一化为s（t）=（t− tm）\/Δt。然后，可以使用矩阵表示[17]来评估位置：

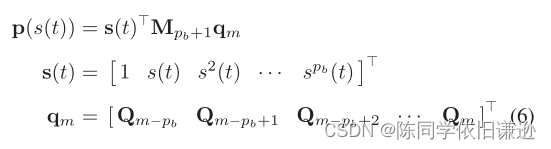
 这里Mpb+1是由pb确定的常数矩阵。在我们的实现中，pb设置为3。导数的计算完全相同，因为B样条的导数也是B样条。

B样条曲线的凸包特性（图3）对于设计优化公式至关重要。我们第IV-B节中展示，这对于确保整个弹道的动态可行性和安全性非常有用。

B、凸包性质

凸包特性（图3）在我们的方法中广泛使用，以确保动态可行性和安全性。

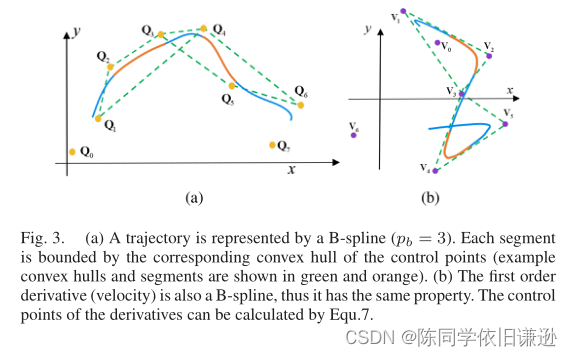
 对于动态可行性，约束所有速度和加速度控制点{V0，V1，…，VN就足够了−1} 和{A0，A1，…，AN−2} 因此Vi∈ [−vmax，vmax]3和Ai∈ [−amax，amax]3。Vi和Ai由等式7计算，其中Δt是结跨度：

 

为了B样条的安全性，我们需要确保它的所有凸包都是无碰撞的。等效地，我们需要确保dh>0，其中dh是任何一个被占据的体素与凸包中的任何一个点Qh之间的距离（图4）。根据三角形不等式，我们得到dh>dc− rh，其中dc是体素与任意一个控制点之间的距离。我们也有rh≤ r12+r23+r34，因为Qh位于凸包内部。组合它们，dh>dc− （r12+r23+r34）始终有效。

因此，如果我们确保：

 则保证凸包是无碰撞的。

C、问题公式

对于由N+1个控制点{Q0，Q1，…，QN}定义的pb次B样条轨迹，我们优化N+1的子集− 2pb控制点{Qpb，Qpb+1，…，QN−pb}。不应更改第一个和最后一个pb控制点，因为它们决定了边界状态。总成本函数定义为：

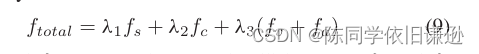
 其中fs和fc是平滑度和碰撞成本。fv和fa是速度和加速度的软限制。λ1、λ2和λ3权衡了平滑性、安全性和动态可行性。

我们通过一个函数来定义平滑度成本fs，该函数捕获了轨迹的几何信息，并且不依赖于时间分配，这与许多最近的工作不同，这些工作使用了平方快速或加加的积分。原因是在优化之后，可以调整时间分配（第五节）。这将改变轨迹的导数，并使优化的快照（加急）变得不那么有意义。我们使用弹性带成本函数2[18]，[19]：

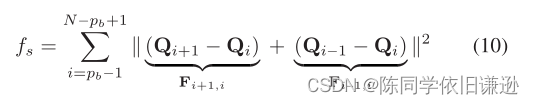
 从物理角度来看，该公式将轨迹视为弹性带，其中每个项Fi+1，i=Qi+1− Qi和Fi−1，i=Qi−1.− Qi是连接节点Qi+1、Qi和Qi的两个弹簧的合力−1、Qi。如果所有项都等于零，所有控制点将均匀分布在一条直线上，这是理想的平滑。

类似地，碰撞成本被公式化为作用在每个控制点上的障碍物的排斥力：

其中d（Qi）是Qi和壁橱障碍物之间的距离。Fc是一个可微分的潜在成本函数，其中dthr指定了障碍物清除的阈值：

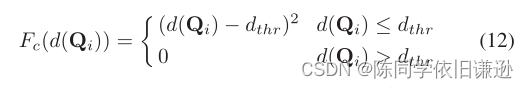
 如第IV-B所示，等式8必须满足，使得轨迹是无碰撞的。由于碰撞成本将控制点推离障碍物，因此dc>0很明显。此外，rj、j+1是可调参数，仅取决于B样条的参数化。实际上，只要我们选择rj，j+1，（j∈ ｛0，1，…，N｝）（在我们的实现中，rj，j+1＜0.2），轨迹在大多数情况下是安全的。在极端情况下，这可能是无效的，例如，环境非常混乱。即使如此，我们也可以重新参数化B样条以选择更小的rj，j+1，之后等式8仍将被满足。

我们惩罚沿轨迹的速度或加速度超过最大允许值vmax和amax，代价类似于等式12。一维速度vμ的惩罚为：

 其中μ∈ {x，y，z}。加速度惩罚具有相同的形式。应用凸包属性（图3），我们定义了fv和fa，从而惩罚不可行的速度和加速度控制点：

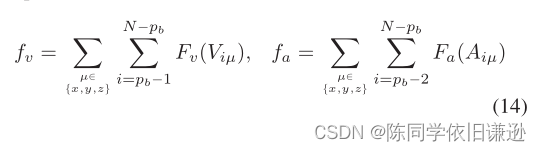
 V、时间分配

虽然我们在路径搜索和优化中约束了动力学可行性，但有时我们会得到不可行的轨迹。基本原因是梯度信息往往会延长整个轨迹，同时将其推离障碍物。因此，四旋翼必须更积极地飞行，以便在同一时间内行驶更长的距离，如果原始运动已经接近物理极限，这不可避免地会导致过度积极的运动。

为了保证动态可行性，我们采用了基于导数控制点和非均匀B样条的时间分配（节点跨度）之间的关系的时间调整方法。由于这种关系，我们可以通过调整相关的时间分配来改变我们预期的飞行攻击性。因此，可以在没有过度保守约束的情况下确保动态可行性。

我们首先介绍了时间调整的数学基础。然后是算法。算法2是为了解决过度攻击的轨迹。

 A、非均匀B样条曲线

非均匀B样条是一种更为普遍的B样条。与均匀B样条曲线的唯一区别是其每个节点跨度Δtm=tm+1− tm独立于他人。非均匀B样条的一阶导数和二阶导数V？i和A？i可以通过以下公式计算：

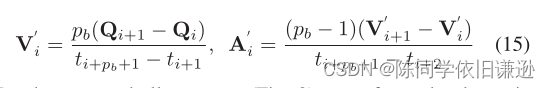
 通过凸包特性（图3），为了加强由非均匀B样条表示的轨迹的动态可行性，在可行域内加强一阶导数和二阶导数的所有控制点就足够了。我们证明，这可以通过改变第V-B节中不可行控制点的相应结跨度来实现。

 B、节点跨度调整

让V？i=[V？i，x，V？i、y、V？i和z]？是不可行的速度控制点。让V？i、 μ是最大的不可行分量，|V？i、 μ|=vm。来自Equ。15我们知道V？i、 μ受持续时间ti+pb+1的影响− ti+1。如果我们将此持续时间更改为⑪ti+pb+1− ti+1=μv（ti+pb+1− ti+1），则V？i、 μ更改为：

 因此，如果我们设置μv=vmvmax，那么速度是可行的，因为|⑪Vi，μ|=vmaxvm|v？i、 μ|=vmax∈ [−vmax、vmax]。

加速可行性的实施是类似的。我们知道A？i、 μ实际上受到ti+pb+2的影响− ti+1，因为它与V？i、 μ和V？i+1，μ。我们改变Δtm=tm+1− m的tm至Δûtm=μaΔtm∈ {i+1，i+2，…，i+pb+1}，我们得到：

 类似地，设μa=（amamax）1 2，则|⑪Ai，μ|=amaxam|a？i、 μ|=amax∈ [−amax、amax]。

C、迭代时间调整

根据第V-B算法。2来增强动态可行性。它迭代地找到轨迹的不可行速度和加速度控制点V和A（第2行），并调整相应的结跨度（第3-10行）。因为结跨度Δtm影响几个控制点，反之亦然，所以边界μ？v和μ？αv和αa两个常数略大于1（第5行，第9行），可防止任何时间跨度过度延长。

VI、实施细节

A、实验设置

本文中提出的运动规划方法在C++11中使用通用非线性优化求解器NLopt实现。4在所有实验中，我们为路径搜索设置r=2，τ=0.5，为优化设置λ1=1 0.0，λ2=0.8，λ3=0.01，为时间调整设置αa=αv=1.1。我们提供了两组真实世界的实验来验证我们提出的规划方法。

首先，我们在未知的杂乱环境中进行快速自主飞行实验（第VII-B节）。我们使用了自行开发的四旋翼平台（图6（a）），该平台配备了V elodyne VLP-16 3-D激光雷达。LOAM[20]用于估计四旋翼的姿态并生成密集点云图。为了获得用于反馈控制的高速率状态估计，我们通过扩展卡尔曼滤波器（EKF）将基于激光的估计与IMU和声纳测量相融合。包括运动规划、状态估计、映射和控制在内的所有模块都在双核3.00 GHz Intel i7-5500 U处理器上运行，该处理器具有8 GB RAM和256 GB SSD。

然后，在第VII-C节，我们专注于测试我们提出的方法在攻击性飞行中的快速重新规划能力，为此我们使用了更轻、更灵活的四旋翼平台（图6（b））。为了消除机载传感带来的不确定性，运动捕捉系统OptiTrack5提供了精确的姿态反馈，并预先构建了环境地图。运动规划和控制模块在Nvidia TX2计算机上运行。

B、重新规划策略

1） 最近的地平线局部规划：当四旋翼机在未知环境中飞行时，由于感应范围有限，它必须频繁地重新规划其轨迹。为了提高效率，我们采用了后退地平线规划方案，其中轨迹仅在已知空间内生成（图7）。一旦运动基元在该范围之外结束，路径搜索就终止，然后进行优化和时间调整。在未知空间进行规划通常是无用的，因此可以节省这些努力。

 

2） 重新规划触发机制：在两种情况下触发重新规划。首先，如果当前轨迹与新出现的障碍物发生碰撞，则触发触发，这确保一旦检测到任何碰撞，就可以使用新的安全轨迹。其次，以固定的时间间隔调用计划器。它使用最新的环境信息定期更新轨迹。

C、欧氏距离场

我们维护了用于优化的体素网格图的EDF，该EDF由有效的O（n）算法计算[21]，其中n=n 3是更新的体素栅格的数量。为了补偿体素网格图引入的EDF离散化误差，并有利于数值优化，使用三线性插值来提高距离和梯度信息的准确性[14]。EDF的全球更新成本非常高，并且会阻碍对快速自主飞行至关重要的计划模块。为了解决这个问题，我们仅使用增量更新策略更新感测范围内的体素网格[22]。

VII、结果

A、分析与比较

1）路径搜索的比较：我们将路径搜索与方法[23]进行了比较，这两种方法都使用时间最优控制公式来生成原语。在随机部署了100个障碍物的40×40×5m地图上进行了比较，最大速度和加速度极限分别设置为3m/s和2m/s2。由于体素网格的分辨率是我们所提出方法性能的关键因素，因此使用不同的分辨率进行综合评估（表I，第1列，第3-5行）。为了公平比较，我们使用了[23]的开源实现。结果列于表I。

如静力学所示，这两种方法都生成了运动学可行轨迹。我们的方法以一个数量级的速度更快，并且倾向于生成持续时间更短的路径。然而，它的控制成本略高。当体素网格变得更粗时，我们的方法的效率提高，但代价是控制成本更高，成功率更低。这种趋势是意料之中的，因为使用更粗的体素网格修剪图元会导致更低的搜索复杂度，而会丢失更可行（甚至更优越）的路径。

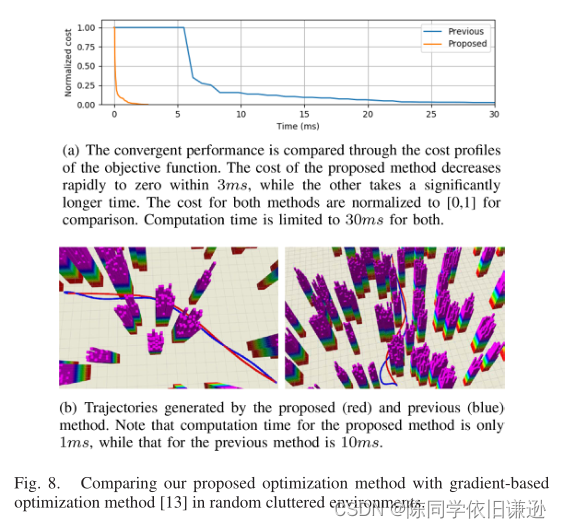
2）优化的比较：对于后端轨迹优化，我们与之前的工作进行了比较[13]。我们之前的方法和提出的方法都利用EDF进行非线性优化。为了公平起见，我们使用路径搜索给出的相同路径作为初始值。首先，我们比较了两种方法的目标函数相对于时间的成本（图8（a））。显然，所提出的方法的成本在最初几毫秒内迅速下降，而另一种方法的下降速度要慢得多。其次，如图8（b）和表II所示，对平滑度（平方加加速度的积分）进行了比较。尽管所提出的方法所用的时间较少，但得到的轨迹更平滑。

 B、机载自主飞行

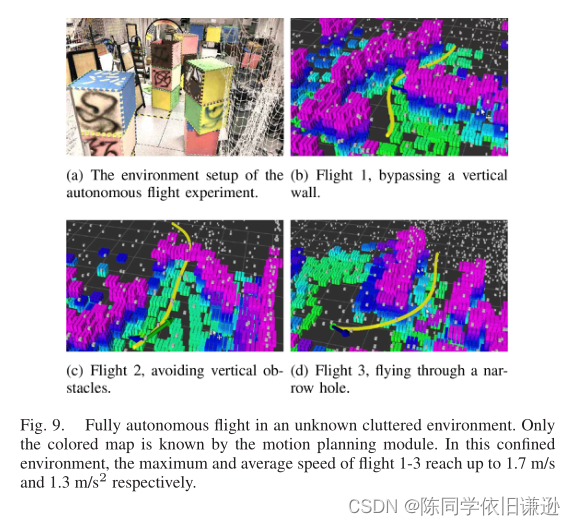
我们在具有挑战性的未知环境中进行了完全自主的快速飞行实验（图9（a））。为了进一步挑战我们的方法，我们使用以四旋翼为中心的半径为5m的球体修剪全局地图，并仅使用该球体内的地图生成轨迹（图9（b）–9（d）），这比我们的真实感知范围小得多。非结构化环境、有限的感知范围以及高飞行速度对运动规划模块构成了挑战，因为它应该在突然出现新威胁时持续快速地重新生成轨迹。我们请读者参阅视频附件以了解更多详细信息。

 C、侵略性飞行

攻击性飞行实验在图10所示的环境中进行。在实验中，四旋翼的目标被人类不断地任意改变。一旦设定了新的目标，就会立即重新规划并执行新的轨迹。最大速度和加速度分别设置为2.5 m/s和1.5 m/s2。这项任务在几个方面具有挑战性。由于飞行是积极的，目标的变化是突然的，运动规划模块应在相当短的时间内生成新的轨迹，以快速对变化作出反应，从而使四旋翼的运动是连续的和平滑的。此外，由于环境受限且杂乱，很难在很短的时间内生成平滑、安全且动态可行的轨迹。该实验验证了我们的方法在可行性的前提下可以生成攻击性运动。它还表明，即使在攻击性飞行过程中目标突然改变，我们的方法也可以在复杂环境中快速生成新的轨迹。视频中还包括更多细节。

 VIII、总结

本文中，我们提出了一种用于四旋翼自主导航的在线运动规划方法。我们将在线快速运动规划问题解耦为前端动态路径搜索和后端非线性轨迹优化。我们采用动态路径搜索来找到安全、动态可行且时间最短的初始路径，通过基于梯度的优化进一步提高了初始路径的平滑度和间隙。通过利用B样条曲线的凸包特性，与以前的基于梯度的规划方法相比，我们显著提高了优化的效率和收敛速度。最后，通过将轨迹表示为非均匀B样条，我们根据给定的预期飞行攻击性调整时间分配。我们在各种复杂环境和仿真中验证了我们提出的方法。该方法的能力也在具有挑战性的现实世界任务中得到验证。

未来，我们计划在大规模或动态环境等极端情况下挑战四旋翼系统。此外，我们将把轨迹优化方法扩展到群体问题。