2024年MathorCup数模竞赛C题完整论文首发

【腾讯文档】2024年妈杯+认证杯资料汇总说明

https://docs.qq.com/doc/DSExyRGhNUm1pTHh4

下面为成品论文部分正文，文末免费赠送数据预处理（py+ma两组代码）

物流网络分拣中心货量预测及人员排班

摘要

随着电商行业的持续发展和消费者需求的不断变化，分拣中心作为物流网络中的关键节点，其管理效率的提升显得尤为重要。本文将基于题目给出的数据，进行分拣中心货量预测及人员排班。

对于问题一，对57 个分拣中心未来 30 天每天及每小时的货量进行预测。首先利用python将不用分拣中心的数据进行分开处理，利用q-q图以及K-S检验判定数据分布方式。对于正态分布数据，使用3西格玛原则判定异常值；对于非正态分布数据，使用箱型图判定异常值。对于判定的结果结合实际情况进行分析处理。利用处理后的数据，进行ADF单位根检验对于通过检验的数据，我们认定为平稳数据使用ARIMA模型，对于未通过检验的数据我们使用LSTM进行预测。对于每小时的货量的预测，我们建立季节性自回归综合移动平均模型进行预测。

对于问题二，对57个分拣中心未来 30 天每天及每小时的货量进行预测。我们对附件三、四进行合并。利用始发分拣中心、到达分拣中心、路线、货量作为特征进行构建随机森林模型对附件四新的路线进行预测货量。利用新老路线货量数据，计算变化率，使用该变化率对问题一预测结果进行放缩实现对问题二57个分拣中心未来 30 天每天及每小时货量的预测。

对于问题三，要求在每天的货量处理完成的基础上，安排的人天数尽可能少，且每天的实际小时人效尽量均衡。我们构建以总人天数为目标函数，xij、yij第 i 天第 j 个班次的正式工、临时工人数作为决策变量。以每班次的总分拣量不能少于预测货量、正式工使用不超过60人、人员非负性约束、正式工每天最多出勤一个班次、添加约束保证人效接近平均值作为约束条件进行求解。

对于问题四，要求在每天货量处理完成的基础上，安排的人天数尽可能少，每天的实际小时人效尽量均衡且正式工出勤率尽量均衡。在问题三的基础上，正式工出勤率尽量均衡，用出勤率方差作为新约束条件，构建xi,j,k，第 i 天第 j 个班次是否有第 k 名正式工出勤作为新的约束条件进行求解。

关键词：货量预测、人员排班、时间序列预测、多目标优化

一、模型假设

为了方便模型的建立与模型的可行性，我们这里首先对模型提出一些假设，使得模型更加完备，预测的结果更加合理。

1.假设给出的数据均为真实数据，真实有效。

2.假设对于一些较为异常的数据的出现具有一定的合理性。

3.假设我们对数据中缺失值的处理方式不会对预测结果造成太大的误差。

4.假设给出的脱敏数据没有造成数据的损坏。

5.假设新旧路线的变化直接影响到货量的增减，且这种影响可以通过历史数据来量化和预测。

6.假设所有的人员排班都遵守当地的劳动法规，包括工作时间、连续工作日数限制和休息时间等

7.假设每个分拣中心都可以根据需求调整正式工和临时工的人数，且临时工的调整可以在短时间内进行。

8.对于特定分拣中心的排班，假设需要平衡正式工的出勤率，使其不超过85%，并且尽量均匀分配工作日，以避免劳动力集中和疲劳

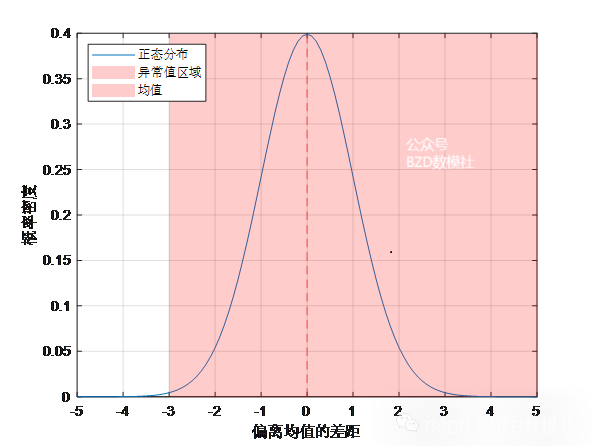
对于服正态分布的数据，例如最大振幅 (平滑化的太阳黑子）等，我们以最大振幅为例进行说明，利用matlab绘制原则的结果图如下所示， 

 

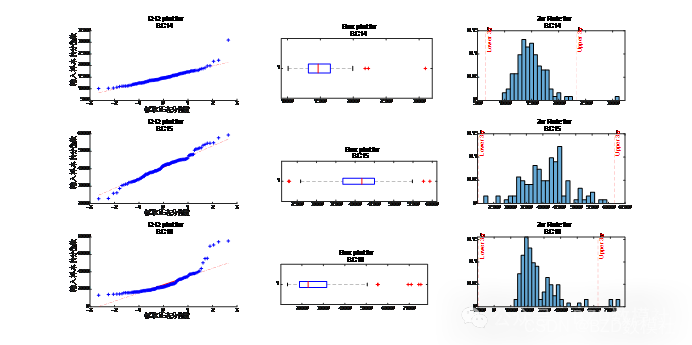
3. 定义适应度函数

适应度函数用来评估粒子的优劣，它应当直接对应于优化问题的目标函数和约束。在这个问题中，适应度函数可以定义为目标函数的值，同时对不满足的约束进行惩罚：

def fitness(particle):

cost = sum(particle)  # 假设particle已经计算了总人天数

penalty = 0

# 检查约束，不满足的约束增加惩罚

for constraint in constraints:

if not constraint(particle):

penalty += large_number  # large_number是一个大数值，用于对适应度函数进行重大惩罚

return cost + penalty

4. 更新粒子

在每次迭代中，更新每个粒子的速度和位置。更新规则依据粒子的个体最优位置和全局最优位置：

for particle in particles:

for i in range(len(particle)):

r1, r2 = random(), random()  # 随机数

# 更新速度

velocity[i] = w * velocity[i] + c1 * r1 * (pbest[i] - particle[i]) + c2 * r2 * (gbest[i] - particle[i])

# 更新位置

particle[i] += velocity[i]

# 确保位置在合法范围内

particle[i] = max(min(particle[i], max_limit[i]), min_limit[i])

% 数据加载
 
data = readtable('附件1.csv', 'Encoding', 'UTF-8');
 
% 转换日期格式
 
data.x____ = datetime(data.x____, 'InputFormat', 'yyyy/MM/dd');
 
% 按分拣中心分组
 
g = findgroups(data.x_______);
 
% 计算分拣中心的数量
 
total_centers = max(g);
 
num_plots = ceil(total_centers / 3); % 每个图三个分拣中心
 
% 对每组三个分拣中心生成一个图
 
for plot_index = 0:num_plots-1
 
figure;
 
centers = unique(data.x_______);
 
centers = centers(1 + plot_index * 3:min(end, 3 + plot_index * 3));
 
for i = 1:length(centers)
 
center = centers(i);
 
idx = ismember(data.x_______, center);
 
series = data.x_____1(idx);
 
% Q-Q图
 
subplot(3, 3, 3 * (i - 1) + 1);
 
qqplot(series);
 
title(['Q-Q plot for ', center]);
 
% 箱型图
 
subplot(3, 3, 3 * (i - 1) + 2);
 
boxplot(series, 'Orientation', 'horizontal');
 
title(['Box plot for ', center]);
 
% 3σ原则
 
subplot(3, 3, 3 * (i - 1) + 3);
 
histogram(series, 30, 'Normalization', 'probability');
 
meanVal = mean(series);
 
stdVal = std(series);
 
xline(meanVal - 3 * stdVal, 'r--', 'Label', 'Lower 3σ');
 
xline(meanVal + 3 * stdVal, 'r--', 'Label', 'Upper 3σ');
 
title(['3σ Rule for ', center]);
 
end
 
end
 
% 按分拣中心分组
 
[g, centers] = findgroups(data.x_______);
 
% 初始化结果表格
 
ks_results = table('Size', [0 3], 'VariableTypes', {'string', 'double', 'double'}, ...
 
'VariableNames', {'分拣中心', '统计量', 'p值'});
 
% 遍历每个分拣中心，执行K-S检验
 
for i = 1:max(g)
 
series = data.x_____1(g == i);
 
% 计算正态分布的参数
 
[mu, sigma] = normfit(series);
 
% 执行K-S检验
 
[statistic, p_value] = kstest(series, 'CDF', [series, normcdf(series, mu, sigma)]);
 
% 保存结果
 
ks_results = [ks_results; {centers(i), statistic, p_value}];
 
end
 
% 保存到Excel文件
 
writetable(ks_results, 'K-S检验结果.xlsx');

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
 
# 数据加载
data_path = '附件1.csv'
data = pd.read_csv(data_path, encoding='GBK')
 
# 按分拣中心分组
grouped = data.groupby('分拣中心')
 
# 选择前三个分拣中心
selected_centers = list(grouped.groups.keys())[:3]
 
# 设置matplotlib的布局
fig, axs = plt.subplots(3, 3, figsize=(18, 12))  # 3行3列
fig.subplots_adjust(hspace=0.4, wspace=0.4)
 
for i, center in enumerate(selected_centers):
    series = grouped.get_group(center)['货量']
 
    # Q-Q图
    stats.probplot(series, dist="norm", plot=axs[0, i])
    axs[0, i].set_title(f'Q-Q plot for {center}')
 
    # 箱型图
    axs[1, i].boxplot(series, vert=False)
    axs[1, i].set_title(f'Box plot for {center}')
 
    # 3σ原则
    mean = series.mean()
    std = series.std()
    lower_bound = mean - 3 * std
    upper_bound = mean + 3 * std
 
    axs[2, i].hist(series, bins=30, alpha=0.7, label='Data Distribution')
    axs[2, i].axvline(lower_bound, color='red', linestyle='dashed', linewidth=1, label='Lower 3σ')
    axs[2, i].axvline(upper_bound, color='red', linestyle='dashed', linewidth=1, label='Upper 3σ')
    axs[2, i].set_title(f'3σ Rule for {center}')
    axs[2, i].legend()
 
plt.show()