一篇文章带你玩转PostGIS空间数据库

一、空间数据库介绍

1.什么是空间数据库

人类理解世界其实是按照三维的角度，而传统的关系型数据库是二维的，要想描述空间地理位置，点、线、面，我们就需要一个三维数据库，即所谓空间数据库。

postGIS就是一个空间数据库。

2.空间数据库是怎么存储的

除了普通数据库所具备的字符串、数值、日期等，空间数据库增加了空间数据类型。

这些空间数据类型抽象并封装了诸如边界（boundary）和维度（dimension）等空间结构。

可以这么理解，空间数据库内置了许多属性，这些属性用于描述空间结构信息。

以点(Point)数据类型为例，一个点可以由它在某一坐标参考系下的X、Y坐标值来表示，如“POINT(116.4074 39.9042)”表示了一个位于北京市中心的点。

并且，空间数据类型按类型层次结构组织。每个子类型继承其父类型的结构（属性）和行为（方法或函数）。

3.空间数据库有索引吗

普通数据库有索引。空间数据库也有空间索引，它有什么作用呢？

举个应用的栗子帮助理解。查找你附近100m以内的所有商场。如果没有空间索引，你需要苦逼的按照坐标取平方根穷举计算，然后保留所有距离小于100的商场数据。

但是空间数据库的索引设计有难点：如何组织数据的结构。普通数据库用B+树等就可以。空间索引有很多种，网格索引、四叉树索引、金字塔索引…

其原理：过于先进，暂不展示

4.空间函数是什么东东

二维的虫子可想不到三维的世界有多复杂：分析几何信息、确定空间关系…

空间数据库当然需要专业的解决这些问题，因此，它内置空间函数。

空间函数主要分为五类：

转换 —— 在geometry（PostGIS中存储空间信息的格式）和外部数据格式之间进行转换的函数
管理 —— 管理关于空间表和PostGIS组织的信息的函数
检索 —— 检索几何图形的属性和空间信息测量的函数
比较 —— 比较两种几何图形的空间关系的函数
生成 —— 基于其他几何图形生成新图形的函数

二、PostGIS快速入门

1.postGIS是什么

其实您应该猜到了，他就是在postgreSQL上的一个插件，但是因为有它，postgreSQL摇身一变，成了一个强大的空间数据库。

这就意味着，这哥们儿开源啊。

2.postGIS怎么用啊

这个教程主要是帮助快速理解什么是postGIS，因此不会太细致。

自行下载安装postGreSQL、postGIS

导入数据文件shape file

一个shapfile必须有的文件：

.shp —— 存储地理要素的几何信息
.shx —— 存储要素几何图形的索引信息
.dbf —— 存储地理要素的属性信息（非几何信息）
可选文件包括：

.prj —— 存储空间参考信息，即地理坐标系统信息和投影坐标系统信息。使用well-known文本格式进行描述。

Soga！原来就是导文件给你可视化展示啊。这题咱会！

操作数据，用SQL
哦，原来还是熟悉的配方，还是原来的味道。

SELECT name
FROM nyc_neighborhoods
WHERE boroname = 'Brooklyn';
1
2
3

元数据管理
PostGIS提供了两张表用于追踪和报告数据库中的几何图形（这两张表中的内容相当于元数据）

第一张表spatial_ref_sys —— 定义了数据库已知的所有空间参照系统，稍后将对其进行更详细的说明。
第二张表（实际上是视图-view）geometry_columns —— 提供了数据库中所有空间数据表的描述信息

通过查询该表，GIS客户端和数据库可以确定检索数据时的预期内容，并可以执行任何必要的投影、处理、渲染而无需检查每个几何图形（geometry）—— 这些就是元数据所带来的作用。

表示真实世界的对象
Simple Features for SQL（SFSQL）规范是PostGIS开发的原始指导标准，它定义了如何表示真实世界的对象。但是这个哥们只表示了二维，而PostGIS扩展了3维、4维的表示。

说人话，就是可以表示：点、线串、多边形、图形集合(Collection)。

举一个图形集合的例子。

SELECT name, ST_AsText(geom)
FROM geometries
WHERE name = 'Collection';
1
2
3

返回结果就是一个点和一个多边形的集合。

基本操作而已，你是不是也学会了。

几何图形的存储
PostGIS支持以多种格式进行几何图形的输入和输出：

• Well-known text（WKT）
• Well-known binary（WKB）
• Geographic Mark-up Language（GML）
• Keyhole Mark-up Language（KML）
• GeoJson
• Scalable Vector Graphics(SVG）

使用方法就是调用encode函数，以下SQL查询展示了一个WKB表示形式的示例

SELECT encode(
  ST_AsBinary(ST_GeometryFromText('LINESTRING(0 0,1 0)')),
  'hex');
1
2
3

由于WKT和WKB是在SFSQL规范中定义的，因此它们不能处理3维或4维的几何图形。对于这些情况，PostGIS定义了Extended Well Known Text（EWKT）和Extended Well Known Binary（EWKB）格式以用于处理3维或4维的几何图形。

数据类型转换
PostgreSQL包含一个简短形式的语法，允许数据从一种类型转换到另一种类型，即类型转换语法：

olddata::newtype
1

例如，将double类型转换为文本字符串类型：

SELECT 0.9::text;
1

搞半天，原来这玩意有手(册)就行，不用太费劲学。

内置函数

这里介绍下它有哪些功能函数，同志们心里有个底，需要时查查手册。

sum(expression) aggregate to return a sum for a set of records
count(expression) aggregate to return the size of a set of records
ST_GeometryType(geometry) returns the type of the geometry
ST_NDims(geometry) returns the number of dimensions of the geometry
ST_SRID(geometry) returns the spatial reference identifier number of the geometry
ST_X(point) returns the X ordinate
ST_Y(point) returns the Y ordinate
ST_Length(linestring) returns the length of the linestring
ST_StartPoint(geometry) returns the first coordinate as a point
ST_EndPoint(geometry) returns the last coordinate as a point
ST_NPoints(geometry) returns the number of coordinates in the linestring
ST_Area(geometry) returns the area of the polygons
ST_NRings(geometry) returns the number of rings (usually 1, more if there are holes)
ST_ExteriorRing(polygon) returns the outer ring as a linestring
ST_InteriorRingN(polygon, integer) returns a specified interior ring as a linestring
ST_Perimeter(geometry) returns the length of all the rings
ST_NumGeometries(multi/geomcollection) returns the number of parts in the collection
ST_GeometryN(geometry, integer) returns the specified part of the collection
ST_GeomFromText(text) returns geometry
ST_AsText(geometry) returns WKT text
ST_AsEWKT(geometry) returns EWKT text
ST_GeomFromWKB(bytea) returns geometry
ST_AsBinary(geometry) returns WKB bytea
ST_AsEWKB(geometry) returns EWKB bytea
ST_GeomFromGML(text) returns geometry
ST_AsGML(geometry) returns GML text
ST_GeomFromKML(text) returns geometry
ST_AsKML(geometry) returns KML text
ST_AsGeoJSON(geometry) returns JSON text
ST_AsSVG(geometry) returns SVG text
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

总的来说，就是可以：求面积、求边界、求大边形里有多少小多边形…在多维的世界里为所欲为。

空间关系

目前为止，我们一次只能处理一个几何图形。

空间数据库之所以强大，是因为它们不仅能存储几何图形，而且还能够分析几何图形之间的关系。

诸如"哪一个是离公园最近的自行车位？"或者"地铁线路和街道的交叉路口在哪里?"这样的问题，只能通过比较、分析表示自行车位、街道和地铁线路的几何图形来回答。

OGC标准定义了以下一组用于比较几何图形的方法。

• ST_Equals(geometry A, geometry B)用于测试两个图形的空间相等性。
• ST_Intersects、ST_Crosses和ST_Overlaps都用于测试几何图形内部是否相交。
• ST_Touches()测试两个几何图形是否在它们的边界上接触，但在它们的内部不相交
• ST_Within()和ST_Contains()测试一个几何图形是否完全包含于另一个几何图形内
• ST_Distance(geometry A, geometry B)计算两个几何图形之间的最短距离

空间连接
空间连接（spatial joins）是空间数据库的主要组成部分，它们允许你使用空间关系作为连接键（join key）来连接来自不同数据表的信息

还支持汇总。JOIN和GROUP BY的组合支持通常在GIS系统中的某些分析。这个和普通的关系型数据库几乎一样。不多介绍了。

随便举个栗子，感受下。

SELECT
  n.name,
  Sum(c.popn_total) / (ST_Area(n.geom) / 1000000.0) AS popn_per_sqkm
FROM nyc_census_blocks AS c
JOIN nyc_neighborhoods AS n
ON ST_Intersects(c.geom, n.geom)
WHERE n.name = 'Upper West Side'
OR n.name = 'Upper East Side'
GROUP BY n.name, n.geom;
1
2
3
4
5
6
7
8
9

上面sql计算了："'Upper West Side’和’Upper East Side’的人口密度（人/平方千米 ）是多少？

三、PostGIS进阶玩法

到目前为止，都平平无奇，接下来介绍进阶玩法。

1.空间索引

空间索引是PostGIS的最大价值之一。在前面的示例中，构建空间连接需要对整个表进行相互比较。这样做的代价很高：连接两个各包含10000条记录的表（每个表都没有索引）将需要进行100000000次比较；如果使用空间索引，则比较次数可能低至20000次

创建索引、删除索引就不多BB了。你们都会。

CREATE INDEX nyc_census_blocks_geom_idx
ON nyc_census_blocks
USING GIST (geom);
1
2
3

注意：USING GIST子句告诉PostgreSQL在构建索引时使用generic index structure（GIST-通用索引结构）。

原理

先回答一个问题，空间索引干了啥？

提高查询效率。

那空间索引是怎么做到提高查询效率的？

标准的数据库索引，是根据被索引的列的值去创建树结构的。空间索引略不同，因为数据库并不能索引几何字段的值 —— 也就是几何对象本身，我们改索引要素的范围边界框。

上图中，和黄色星星相交的线的数量是 1，即红色那条线。但是与黄色框相交的范围框有红色和蓝色，共 2 个。

数据库求解 “什么线与黄色星相交” 这个问题，是先用空间索引求解 “什么范围框与黄色范围框相交” 这个问题的（速度非常快），然后才是 “什么线与黄色的星星相交”。上述过程仅对于第一次测试的空间要素而言。

对于数量庞大的数据表，这种索引先行，然后局部精确计算的 “两遍法” 可以在根本上减少查询计算量。

简单来说就是，规则的几何图形的计算比不规则的图形计算简单，利用这一点做为优化的基本思想。

PostGIS中最常用的函数（ST_Contains、ST_Intersects、ST_DWithin等）都包含自动索引过滤器。但有些函数（如ST_Relate）不包括索引过滤器。

要使用索引执行边界框搜索（即纯索引查询-Index only Query-没有过滤器），需要使用"&&"运算符

查询规划器：用不用索引？
PostgreSQL查询规划器（query planner）智能地选择何时使用或不使用空间索引来计算查询。与直觉相反，执行空间索引搜索并不总是更快。

默认情况下，PostgreSQL定期收集数据统计信息，共查询规划器使用。但是，如果你在短时间内更改了表的构成，则统计数据将不会是最新的。因此，为确保统计信息与表内容匹配，明智的做法是在表中加载和删除大容量数据后手动运行ANALYZE命令。

ANALYZE nyc_census_blocks;
1

清理：回收空间
每当创建新索引或对表大量更新、插入或删除后，都必须执行清理（VACUUMing）。VACUUM命令要求PostgreSQL回收表页面中因记录的更新或删除而留下的任何未使用的空间。

VACUUM ANALYZE nyc_census_blocks;
1

2.数据投影

2.1 数据投影简介

地球不是平的，也没有简单的方法把它放在一张平面纸地图上（或电脑屏幕上），所以人们想出了各种巧妙的解决方案（投影）。

每种投影方案都有优点和缺点，一些投影保留面积特征；一些投影保留角度特征，如墨卡托投影（Mercator）；一些投影试图找到一个很好的中间混合状态，在几个参数上只有很小的失真。所有投影的共同之处在于，它们将（地球）转换为平面笛卡尔坐标系。

使用投影特别简单，PostGIS提供了ST_SRID(geometry）和ST_SetSRID(geometry，SRID）函数。

比较数据
比较坐标需要基于他的SRID（严谨的说应该是空间参考系统），如果不是同一个参考系统，比较没有意义，会返回错误，比如如下实例。

SELECT ST_Equals(
         ST_GeomFromText('POINT(0 0)', 4326),
         ST_GeomFromText('POINT(0 0)', 26918)
         );
1
2
3
4

转换数据
数据可以在不同SRID的进行转换。

SELECT ST_AsText(
 ST_Transform(
   ST_SetSRID(geom,26918),
 4326)
)
FROM geometries;
1
2
3
4
5
6

2.2 地理坐标

坐标为"地理（geographics）“形式，即” 纬度（latitude）/经度（longitude）"形式的数据非常常见。地理坐标不是笛卡尔平面坐标。

如果你的数据在地理范围上是紧凑的（包含在州、县或市内），请使用基于笛卡尔坐标的geometry类型。否则，请使用使用基于球体坐标的Geography。而其中的原因，纯粹是数学上的精确度与性能问题，这里不解释。

坐标数据类型准换前面介绍过，这里复习下。

SELECT code, ST_X(geog::geometry) AS longitude FROM airports;
1

3.几何图形创建函数

目前我们看到的所有函数都可以处理已有的几何图形并返回结果。"几何图形创建函数"以几何图形作为输入并输出新的图形。

3.1 以点代形

组成空间查询时的一个常见需求是将多边形要素替换为要素的点表示。这对于空间连接（spatial join）非常有用，因为在两个多边形图层上使用St_Intersects(geometry, geometry)通常会导致重复计算：位于两个多边形的边界上的多边形将与两侧的多边形都相交，将其替换为点将强制它位于一侧或另一侧，而不是与两侧的多边形都相交

• ST_Centroid(geometry) —— 返回大约位于输入几何图形的质心上的点。这种简单的计算速度非常快，但有时并不可取，因为返回点不一定在要素本身上。如果输入的几何图形具有凹性（形如字母’C’的几何图形），则返回的质心可能不在图形的内部。
  

• ST_PointOnSurface(geometry) —— 返回保证在输入多边形内的点。从计算上讲，它比centroid操作代价要大得多。

3.2 缓冲区

缓冲区操作在GIS工作流中很常见，在PostGIS中也可以进行缓冲区操作。 ST_Buffer(geometry, distance)接受几何图形和缓冲区距离作为参数，并输出一个多边形，这个多边形的边界与输入的几何图形之间的距离与输入的缓冲区距离相等。使用ST_Buffer函数即可。

3.3 重叠、相并

另一个经典的GIS操作 - 叠置（overlay）- 通过计算两个重叠多边形的交集来创建新的几何图形。

使用ST_Intersection(geometry A, geometry B)函数。

ST_Union将两个几何图形合并起来

4.几何图形的有效性

多边形不一定有效，如果无效会报错TopologyException错误。下面是一些有效性规则。

多边形的环必须闭合
内环必须位于外环的内部
环不能自相交（它们不能相互接触，也不能交叉）
除了在某个点接触，环不能与其他环接触

前两条是必须的。后面两条则是非必须设置的。您还可以自定义自洽规则。

ST_IsValid(geometry)函数可以用于检测几何图形的有效性。

可以修复无效的图形，坏消息是：没有100%确定的方法来修复无效的几何图形。

在视觉上修复无效几何图形的一个好工具是OpenJump(http://openjump.org)，它在Tools->QA->Validate Selected Layers.下包含一个验证程序。

现在好消息是：可以使用以下任何一种方法在数据库中修复很大一部分的缺陷：

ST_MakeValid函数
ST_Buffer函数

5.几何图形的相等

在处理几何图形时确定相等可能很困难。PostGIS支持三种不同的函数与操作符，可以用来确定不同级别的相等。

精确相等（ST_OrderingEquals）
精确相等是通过按顺序逐个比较两个几何图形的顶点来确定的，以确保它们在位置上是相同的。如果顶点定义顺序不同，即使是相等也会被认作不相等。

空间相等（ST_Equals）
ST_Equals的函数，可用于测试几何图形的空间相等性或等价性。无论是绘制多边形的方向、定义多边形的起点，还是包含的点的个数的差异在这里都不重要。重要的是多边形包含相同的空间区域，它们就相等。

包围框相等（~=）
为了更快地进行比较，提供了包围框（bounding box）相等运算符 ’ ~= ’ 。这仅在包围框（矩形）上操作，确保几何图形占用相同的二维范围，但不一定占用相同的空间。它不一定精确，但是可以先用它粗筛，再结合其他方法细选。先粗后细。

6.线性参考

线性参考是一种表示要素的方法，这些要素可以通过引用一个基本的线性要素来描述。使用线性参照建模的常见示例包括：

公路资产，这些资产使用公路网络沿线的英里来表示。
道路养护作业，指在一对英里测量之间沿着公路网发生的作业。
水产库存，其中鱼的存在位置被记录为距离上游的一段位置之间。
河流的水文特征，以河流的某一个点到另一个点作为参考。

线性参考到底是个啥？

线性参考是使用沿测量的线状要素的相对位置存储地理位置的方法。

听不懂？

辅助线你总知道吧。其实线性参考就可以理解成一个辅助线，其他位置的计算就算和辅助线的相对位置。比如你以你大哥的身高为参考，计算你比他高了多少，判断你有没有长高(前提是你哥不长个了，误~)

具体可以看如下例子。

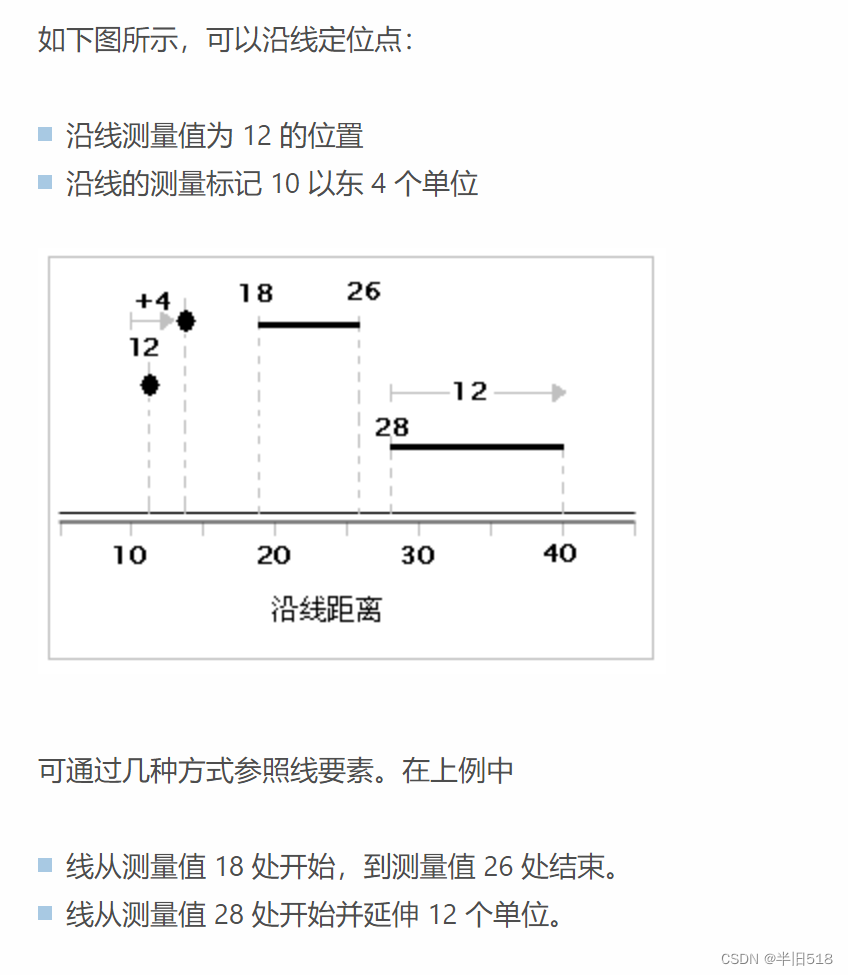
下图是线性参考在交通网中实际的应用，红色的就是线性参考。

用下列的语法可以创建一个一个线性参考。

SELECT ST_LineLocatePoint('LINESTRING(0 0, 2 2)', 'POINT(1 1)');
1

7.DE9IM模型

“维数扩展的9交集模型-Dimensionally Extended 9-Intersection Model”（DE9IM）是一个用于建模两个空间对象如何交互的框架。

首先，每个空间对象都具有：

内部（interior)
边界（boundary）
外部（exterior）

即使是线段、点也有内部、外部和边界。

对线段：内部是以端点为界限的线的那一部分；边界是线性要素的端点；外部是平面中除内部和边界外的所有其他部分。

对于点来说，更奇怪：内部是点，边界是空集，外部是平面上除点以外的所有其他部分。

使用这些内部、外部和边界的定义，任何一对空间要素之间的关系都可以用一对要素的内部/边界/外部/之间九个可能的交集的维数来表征。

注意上面有一个dim参数，规则是：对于上例中的多边形，内部的交集是二维区域，因此矩阵的对应部分用"2"填充。边界仅在零维点处相交，因此对应矩阵部分用"0"填充。

再举一个栗子。

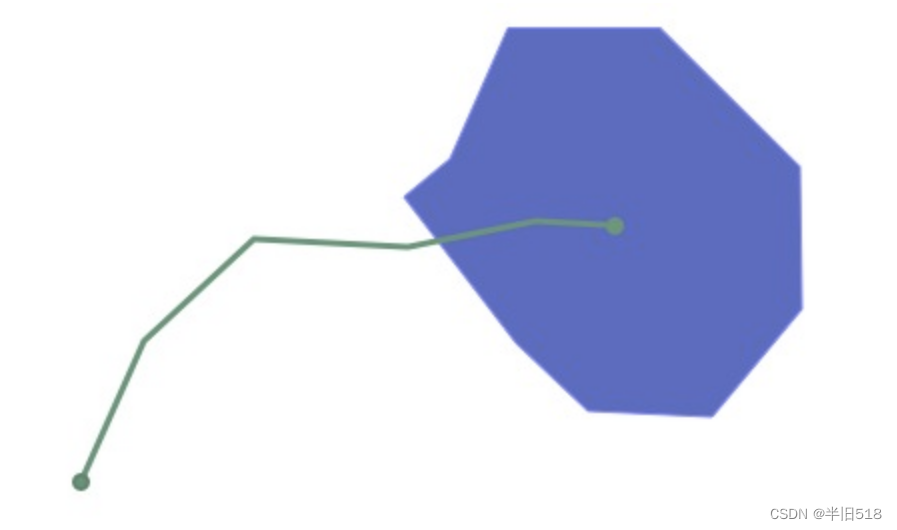
关于它们的交集的DE9IM矩阵如下：

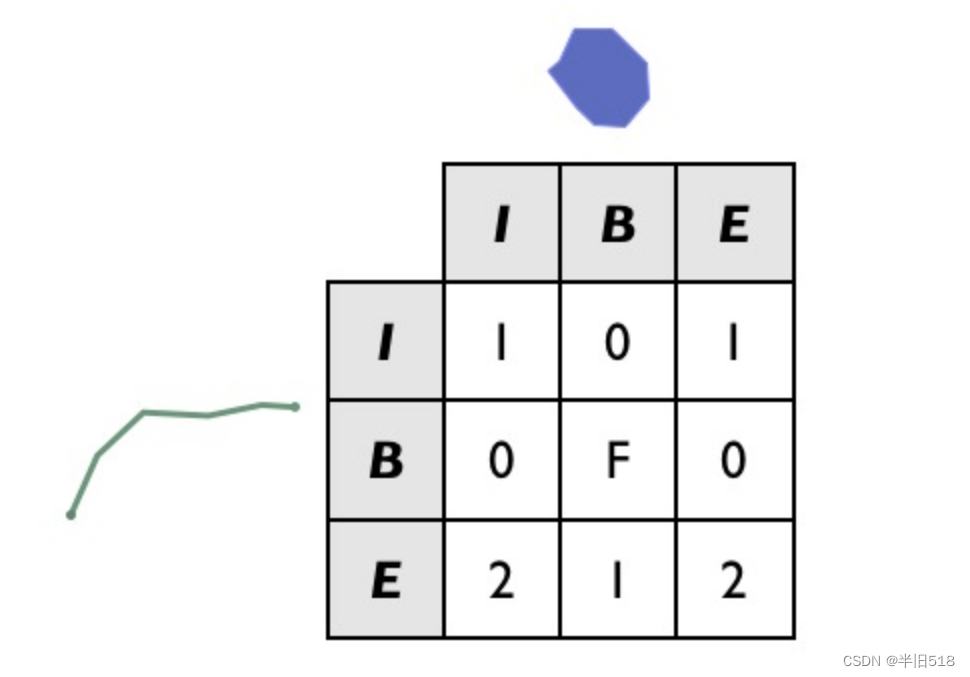
请注意，以上两个要素的边界实际上根本不相交（线的端点与多边形的内部相交，而不是与多边形的边界相交，反之亦然），因此B/B单元用"F"填充。

生成DE9IM模型矩阵的SQL如下。

SELECT ST_Relate(
         'LINESTRING(0 0, 2 0)',
         'POLYGON((1 -1, 1 1, 3 1, 3 -1, 1 -1))'
);
1
2
3
4

DE9IM矩阵的强大之处不在于生成它们，而在于使用它们作为匹配参数来查找彼此之间具有特定关系的几何图形。

假设我们有一个湖泊（Lakes）和码头（Docks）的数据模型，进一步假设码头必须位于湖泊内部，并且必须在一端接触到湖泊的边界。我们能在数据库中找到所有符合这一规则的码头吗？

用下面sql就可以做到，推导过程就不展开了。

SELECT docks.*
FROM docks JOIN lakes ON ST_Intersects(docks.geom, lakes.geom)
WHERE ST_Relate(docks.geom, lakes.geom, '1FF00F212');
1
2
3

8.索引集群

加速数据访问的一种方法是确保可能在同一结果集中一起被检索的记录位于硬盘上的相近物理位置。这就是所谓的"聚簇（clustering）"。

基于空间索引的聚簇对于将通过空间查询访问的空间数据是有意义的：相似的事物往往具有相似的位置（地理学第一定律）。

写个sql,创建一个索引集群。

-- Cluster the blocks based on their spatial index
CLUSTER nyc_census_blocks USING nyc_census_blocks_geom_idx;
1
2

分为两类：

• 基于R-Tree的聚簇
• GeoHash上的集群
  
  可自行深入理解两种算法。

9. 3-D

到目前为止，我们一直在处理2-D几何图形（二维几何图形），只有X和Y坐标。但是PostGIS支持所有几何图形类型额外的维度，对于每个坐标，另外还能支持用于表示高度信息的"Z"维度以及用于添加额外附加信息的"M"维度（通常为时间、道路英里或距离信息）。

有许多函数可用于计算三维对象之间的关系

如果你愿意，甚至可以扩展到N-D。

10.最近领域搜索

KNN是一种基于纯空间索引的近邻搜索方法。这里不展开，你知道有这样的算法就行。

11.使用触发器追踪历史编辑操作

生产环境下数据库的一个常见要求是能够跟踪用户编辑数据的历史：数据在两个日期之间是如何变化的，是谁操作的，以及它们哪些内容变化了？一些GIS系统通过在客户端接口中包含更改管理功能来跟踪用户的编辑数据操作，但这增加了客户端编辑工具的复杂性。

使用数据库和数据库的触发器机制，可以对任何表进行编辑历史跟踪，从而让客户端保持对编辑表的简单“直接编辑”（客户端不用负责追踪编辑历史的功能，只负责CRUD）。

12.用于创建空栅格的ST_MakeEmptyRaster函数

ST_MakeEmptyRaster用于创建一个空的没有像元值的栅格（没有波段），各个参数用于定义这个空栅格的元数据：

width、height —— 栅格的列数和行数
upperleftx、upperlefty —— 对应空间坐标系中栅格左上角的坐标
scalex、scaley —— 单个像元的宽度和长度（单位等同于空间参考坐标系的单位）。
skewx、skewy —— 旋转角度，如果栅格数据北方朝上，该值为0。默认值为0。
srid —— 空间参考坐标系，默认被设置为0。
pixelsize —— 单个像元的宽度和长度。当scalex和scaley相等时，就可以直接使用这个参数设置像元大小。

效果如下