MLP时代已经终结？KAN：全新网络架构一夜爆火！百分之一的参数实现百倍性能！...

点击下方卡片，关注「3D视觉工坊」公众号
选择星标，干货第一时间送达

来源：3D视觉工坊

添加小助理：dddvision，备注：方向+学校/公司+昵称，拉你入群。文末附行业细分群

扫描下方二维码，加入3D视觉知识星球，星球内凝聚了众多3D视觉实战问题，以及各个模块的学习资料：近20门视频课程（星球成员免费学习）、最新顶会论文、计算机视觉书籍、优质3D视觉算法源码等。想要入门3D视觉、做项目、搞科研，欢迎扫码加入！

0. 论文信息

标题：KAN: Kolmogorov-Arnold Networks

作者：Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark

机构：麻省理工学院、加州理工学院、东北大学、美国国家科学基金会人工智能和基本相互作用研究所

原文链接：https://arxiv.org/abs/2404.19756

代码链接：https://github.com/KindXiaoming/pykan

1. 摘要

受科尔莫戈洛夫-阿诺德表示定理的启发，我们提出科尔莫戈洛夫-阿诺德网络（KANs）作为多层感知器（MLPs）的有希望的替代品。虽然MLPs在节点（"神经元"）上有固定的激活函数，但KANs在边缘（"权重"）上有可学习的激活函数。KANs根本没有线性权重-每个权重参数都被参数化为样条的单变量函数所取代。我们表明，这个看似简单的改变使KANs在准确性和可解释性方面优于MLPs。对于准确性，较小的KANs在数据拟合和PDE求解方面可以达到与较大的MLPs相当或更好的准确性。理论上和实证上，KANs具有比MLPs更快的神经缩放规律。对于可解释性，KANs可以直观地可视化，并且可以轻松地与人类用户交互。通过数学和物理学中的两个例子，KANs被证明是有用的合作者，帮助科学家（重新）发现数学和物理定律。总之，KANs是MLPs的有希望的替代品，为进一步改进今天严重依赖MLPs的深度学习模型提供了机会。

2. 引言

多层感知器（MLPs）也被称为全连接前馈神经网络，是当今深度学习模型的基础构建模块。MLPs的重要性无法过分强调，因为它们是机器学习中用于逼近非线性函数的默认模型，这归功于它们由通用逼近定理保证的表达能力。然而，MLPs是我们能够构建的最佳非线性回归器吗？尽管MLPs被广泛使用，但它们存在显著缺点。例如，在Transformer中，MLPs几乎消耗了所有非嵌入参数，并且通常不太可解释（相对于注意力层）而无需后续分析工具。

这篇文章提出了一种有前途的MLPs替代方案，称为Kolmogorov-Arnold Networks（KANs）。虽然MLPs受到通用逼近定理的启发，但KANs受到Kolmogorov-Arnold表示定理的启发。像MLPs一样，KANs具有全连接结构。然而，MLPs在节点（"神经元"）上放置固定的激活函数，而KANs在边缘（"权重"）上放置可学习的激活函数。

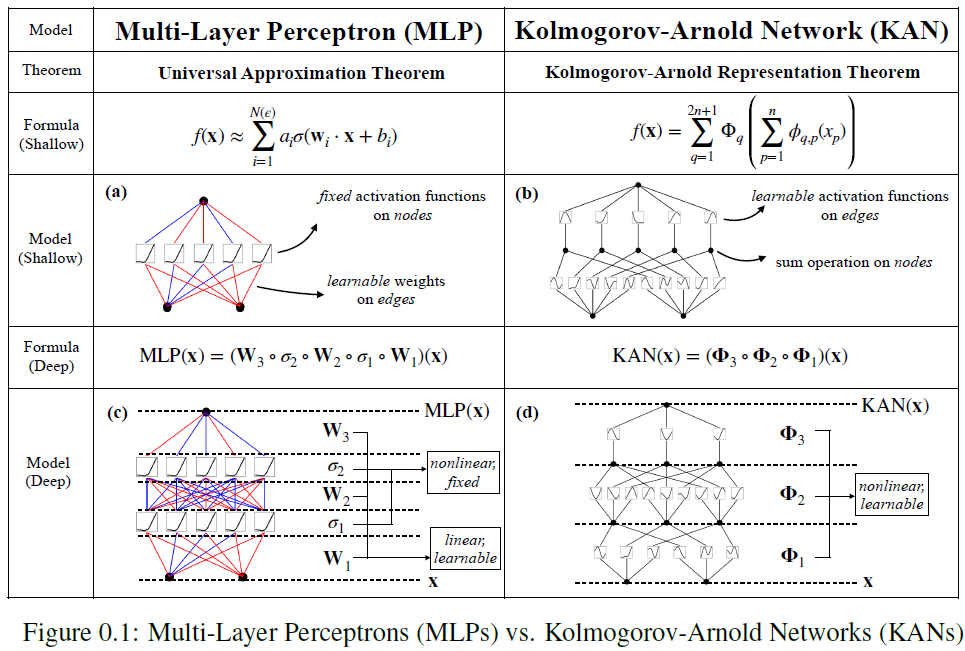
因此，KANs根本没有线性权重矩阵：相反，每个权重参数都被可学习的一维函数取代，该函数被参数化为样条。KANs的节点仅对传入信号进行求和，而不应用任何非线性。人们可能担心KANs是无望的昂贵，因为每个MLP的权重参数都变成了KAN的样条函数。幸运的是，KANs通常允许比MLPs更小的计算图。例如，对于PDE求解，一种2层宽度为10的KAN比一个4层宽度为100的MLP更准确（10^-7 vs 10^-5 MSE），并且参数效率更高（10^2 vs 10^4个参数）。

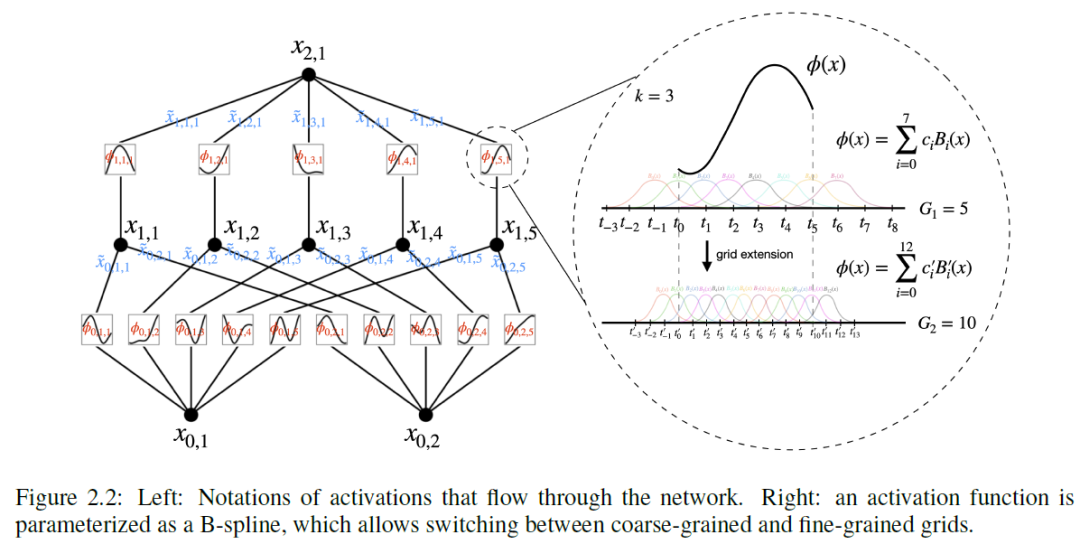
毫不奇怪，使用Kolmogorov-Arnold表示定理构建神经网络的可能性已经被研究过。然而，大多数工作仍停留在原始的深度-2宽度-(2n + 1)表示上，并且没有机会利用更现代的技术（例如反向传播）来训练网络。我们的贡献在于将原始的Kolmogorov-Arnold表示概括为任意宽度和深度，将其置于今天的深度学习世界中，以及利用广泛的经验实验证明其作为AI + Science基础模型的潜在作用，因为其准确性和可解释性。尽管它们有着优雅的数学解释，但KANs只不过是样条和MLPs的组合，利用它们各自的优势，避免各自的弱点。样条对于低维函数精确，易于局部调整，并能在不同分辨率之间切换。然而，由于无法利用组合结构，样条存在严重的维度诅咒（COD）问题。另一方面，MLPs由于其特征学习而不太受COD的影响，但在低维度上比样条不太精确，因为其无法优化单变量函数。为了准确地学习一个函数，模型不仅应该学习组合结构（外部自由度），还应该很好地逼近单变量函数（内部自由度）。KANs就是这样的模型，因为它们在外部有MLPs，在内部有样条。因此，KANs不仅可以学习特征（由于它们与MLPs的外部相似性），而且可以将这些学习到的特征优化到很高的精度（由于其与样条的内部相似性）。例如，MLPs可能会学习到广义可加结构，但对于近似指数和正弦函数，使用ReLU激活是非常低效的。相比之下，KANs可以很好地学习组合结构和单变量函数，因此大大优于MLPs。

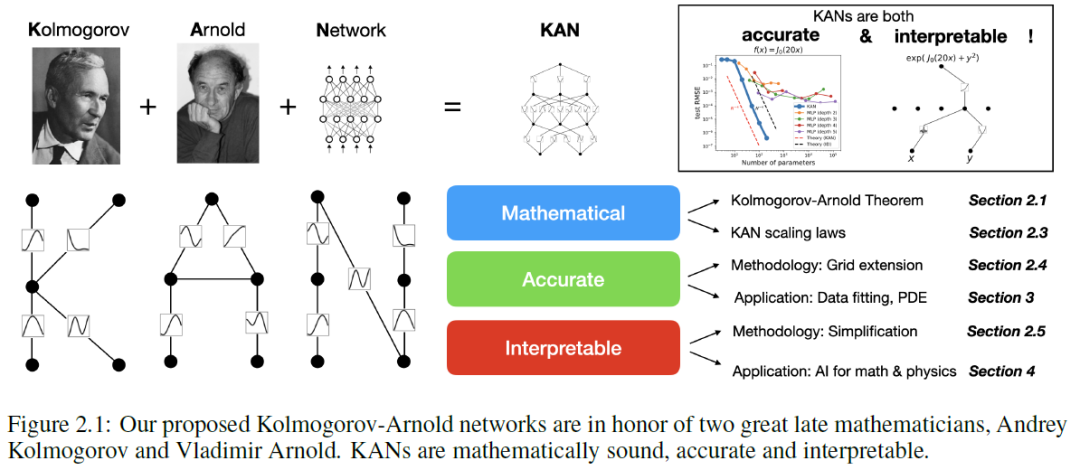
在本文中，我们将使用大量的数值实验来证明KANs相对于MLPs可以带来显著的精度和可解释性改进。文章的组织结构如图2.1所示。首先介绍KAN架构及其数学基础，介绍网络简化技术以使KANs更易解释，并介绍网格扩展技术以使KANs的精度越来越高。然后展示KANs比MLPs在数据拟合和PDE求解方面更准确：当数据中存在组合结构时，KANs可以战胜维度诅咒，达到比MLPs更好的扩展规律。之后展示KANs是可解释的，并且可以用于科学发现。使用数学（结实论）和物理（安德森定位）中的两个例子来证明KANs可以帮助科学家"合作"（重新）发现数学和物理定律。最后总结了相关工作，并通过讨论广泛的影响和未来方向来总结。

3. KAN的精确性

3.1 玩具数据集

为了检验，我们构建了五个例子，知道它们具有光滑的 KA 表示：

(1) f(x) = J_0(20x)，这是贝塞尔函数。由于它是一个单变量函数，它可以用样条表示，这是一个 [1, 1] KAN。

(2) f(x, y) = exp(sin(pi x) + y^2) 。我们知道它可以被一个 [2, 1, 1] KAN 精确表示。

(3) f(x, y) = xy。我们知道它可以被一个 [2, 2, 1] KAN 精确表示。

(4) 一个高维例子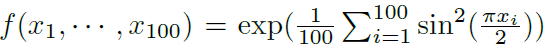： 可以被表示为一个 [100, 1, 1] KAN。

(5) 一个四维例子 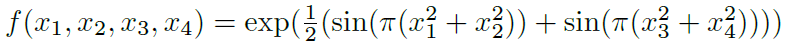，可以被表示为一个 [4, 4, 2, 1] KAN。

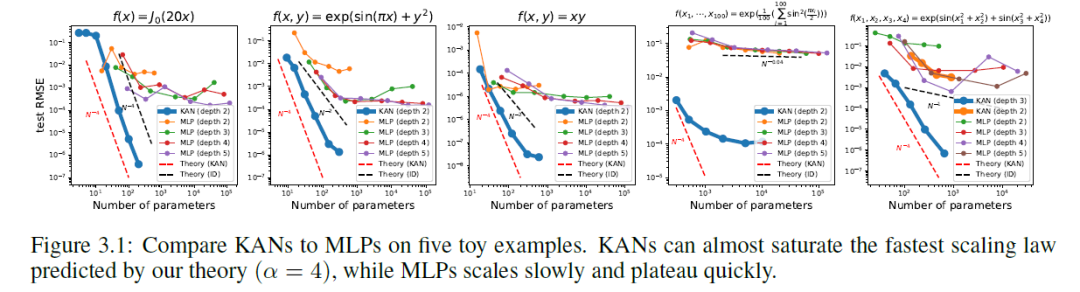
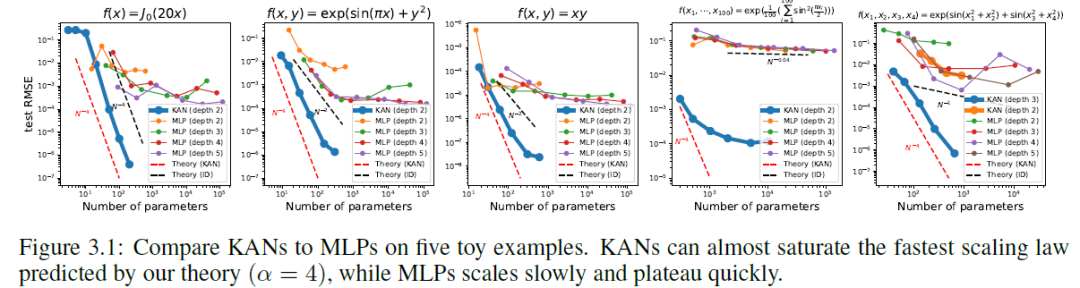
我们通过每200步增加一次网格点的方式训练这些 KAN，总共覆盖了 G ={3, 5, 10, 20, 50, 100, 200, 500, 1000}。我们将 MLPs 作为基线，用不同深度和宽度进行训练。MLPs 和 KANs 都使用 LBFGS 总共训练 1800 步。我们在图 3.1 中绘制了 KANs 和 MLPs 的测试 RMSE 作为参数数量的函数，表明 KANs 的缩放曲线比 MLPs 更好，特别是对于高维例子。为了比较，我们绘制了从我们的 KAN 理论预测的红色虚线 (α = k+1 = 4)，以及从 Sharma & Kaplan预测的黑色虚线 (α = (k+1)/d = 4/d)。KANs 几乎可以达到更陡的红线，而 MLPs 甚至无法像较慢的黑线那样快速收敛，并且很快就会达到平稳状态。我们还注意到，对于最后一个例子，2 层 KAN [4, 9, 1] 的表现要比 3 层 KAN (形状 [4, 2, 2, 1]) 差得多。这突显了更深的 KANs 和 MLPs 的更大表达能力，对于 MLPs 也是一样的：深层 MLPs 比浅层的表达能力更强。

3.2 特殊函数

以上结果的一个警告是，我们假设"真实"的 KAN 形状是已知的。在实践中，我们并不知道 KA 表示的存在。即使我们保证存在这样的 KA 表示，我们也不知道 KAN 形状是先验的。在多于一个变量的特殊函数中，这样的情况就会出现，因为如果多元特殊函数 (例如，贝塞尔函数)能够被 KA 表示，只涉及一元函数和求和，这在数学上是令人惊讶的。我们将在下面展示：

(1) 找到特殊函数的 (近似) 紧凑 KA 表示是可能的，从 Kolmogorov-Arnold 表示的角度揭示了特殊函数的新数学性质。

(2) KANs 在表示特殊函数方面比 MLPs 更有效和准确。

我们收集了数学和物理中常见的 15 个特殊函数，总结在表 2 中。我们选择了固定宽度为 5 或 100 的 MLPs，并在 {2, 3, 4, 5, 6} 中扫描深度。我们同时使用修剪和不修剪的 KANs。不修剪的 KANs：我们固定 KAN 的形状，宽度设为 5，深度在 {2,3,4,5,6} 中扫描。修剪的 KAN：我们使用第 2.5.1 节中的稀疏化 (λ = 10^{-2} 或 10^{-3}) 和修剪技术，从固定形状的 KAN 中获得一个较小的 KAN。每个 KAN 被初始化为 G = 3，使用 LBFGS 进行训练，每 200 步增加一次网格点以覆盖 G = {3, 5, 10, 20, 50, 100, 200}。对于每种超参数组合，我们运行 3 个随机种子。

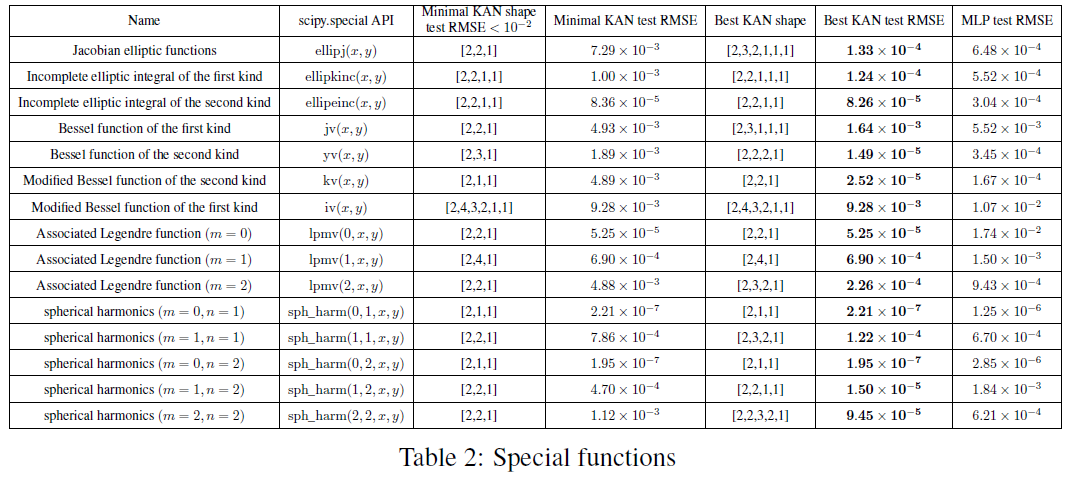
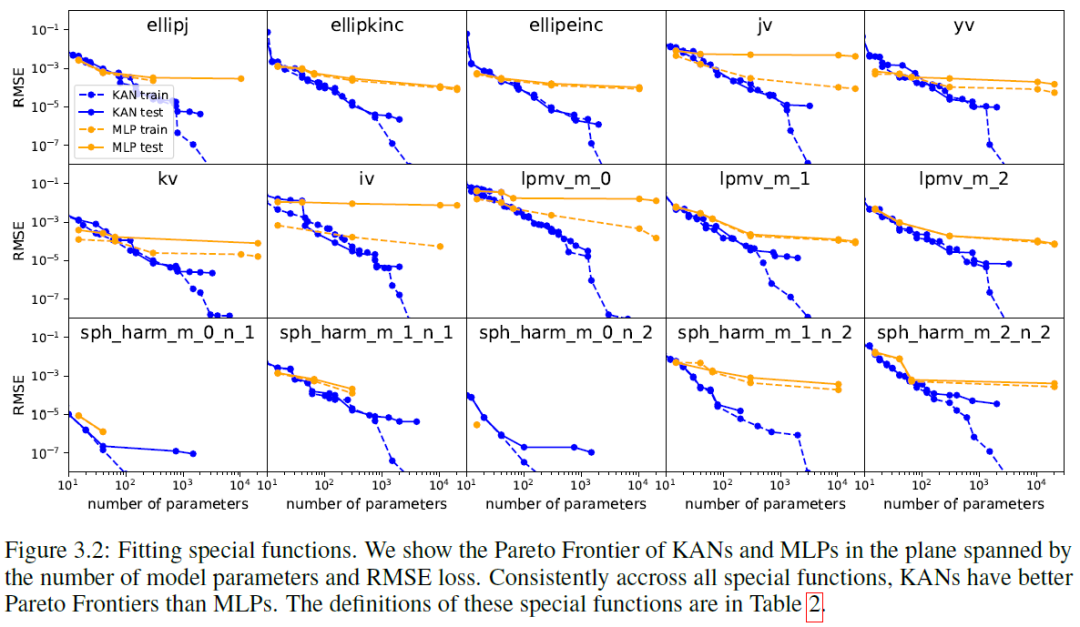
对于每个数据集和每个模型系列 (KANs 或 MLPs)，我们在 (参数数量，RMSE) 平面上绘制 Pareto 前沿线，如图 3.2 所示。KANs 的性能始终优于 MLPs，即在相同数量的参数情况下，KANs 可以实现比 MLPs 更低的训练/测试损失。此外，我们在表 2 中报告了我们自动发现的特殊函数的 KANs 的 (令人惊讶的紧凑) 形状。从数学上解释这些紧凑表示是有趣的一方面。另一方面，这些紧凑表示意味着可以将高维查找表分解为几个 1D 查找表，这可能会节省大量内存，而在推断时执行几次加法的开销几乎可以忽略不计。

3.3 费曼数据集

第3.1节的设置是当我们清楚知道"真实"的KAN形状时。第3.2节的设置是当我们清楚不知道"真实"的KAN形状时。这部分研究的是介于两者之间的设置：考虑到数据集的结构，我们可以手动构建KAN，但我们不确定它们是否是最优的。在这种情况下，比较人工构建的KAN和通过修剪自动发现的KAN是有趣的。费曼数据集收集了来自费曼教科书的许多物理方程[20, 21]。对于我们的目的，我们感兴趣的是费曼数据集中至少有2个变量的问题，因为对于KAN来说，一元问题是微不足道的(它们简化为1D样条)。来自费曼数据集的一个样本方程式是相对论速度加法公式 f(u, v) = (u + v)/(1 + uv)。可以通过随机抽取ui ∈ (−1, 1)，vi ∈ (−1, 1)，并计算fi = f(ui, vi)来构造数据集。鉴于许多元组(ui, vi, fi)，我们训练一个神经网络，并旨在从u和v预测f。

我们感兴趣的是(1)神经网络在测试样本上的表现如何；(2)我们可以从神经网络中了解到关于问题结构的多少信息。

我们比较了四种类型的神经网络：(1) 人工构造的KAN。给定一个符号公式，我们将其重写为Kolmogorov-Arnold表示。构建的形状列在表3的"人工构造的KAN形状"中。(2) 不带修剪的KAN。我们将KAN形状固定为宽度5，并在{2,3,4,5,6}中扫描深度。(3) 带修剪的KAN。(4) MLPs，固定宽度为20，深度在{2, 3, 4, 5, 6}中扫描，并从{Tanh, ReLU, SiLU}中选择激活函数。每个KAN被初始化为G = 3，使用LBFGS进行训练，每200步增加一次网格点以覆盖G = {3, 5, 10, 20, 50, 100, 200}。对于每种超参数组合，我们尝试了3个随机种子。对于每个数据集(方程)和每种方法，我们报告了在随机种子和深度上获得最佳模型(最小KAN形状或最低测试损失)的结果。在表3中。我们发现MLPs和KANs在平均水平上行为相似。对于每个数据集和每个模型系列(KANs或MLPs)，我们在参数数量和RMSE损失组成的平面上绘制了Pareto前沿。

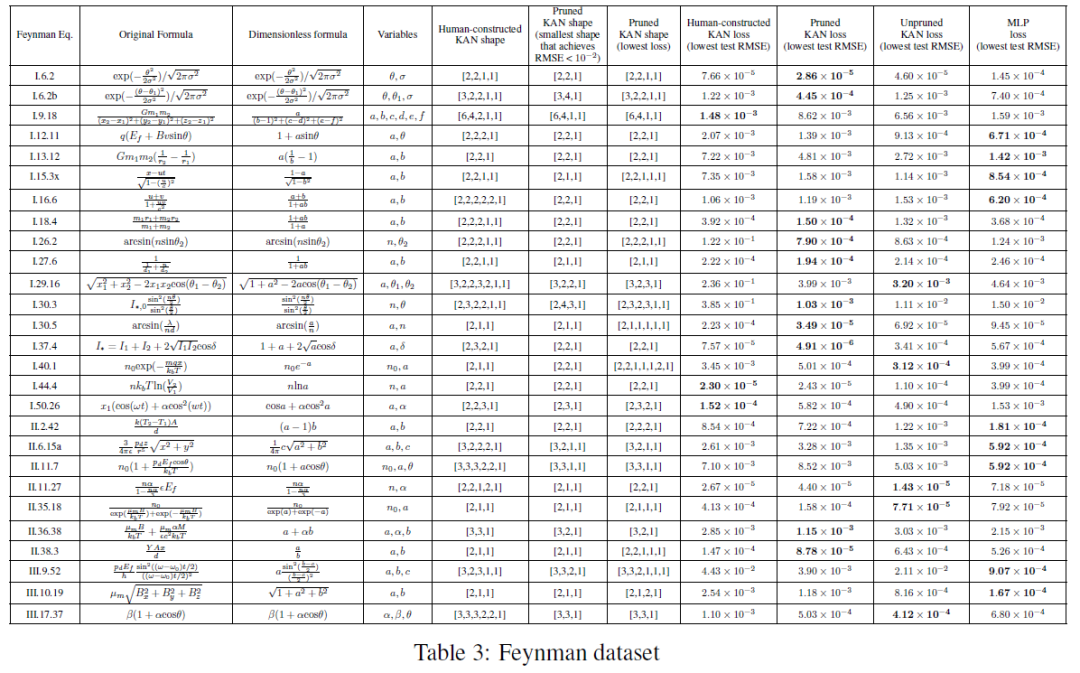
我们推测，费曼数据集太简单了，以至于KANs无法进一步改进，因为变量的依赖性通常是平滑或单调的，这与特殊函数的复杂性形成对比，特殊函数通常表现出振荡行为。自动发现的KAN比人工构造的更小。我们在表3的两列中报告了修剪KAN的形状；一列是为了实现合理的损失(即测试RMSE小于10−2)而得到的最小修剪KAN形状；另一列是为了实现最低测试损失而得到的修剪KAN形状。有趣的是观察到自动发现的KAN形状(最小和最佳)通常比我们的人工构造要小。这意味着KA表示可能比我们想象的更高效。与此同时，这可能会使解释变得微妙，因为信息被压缩到比我们熟悉的空间更小的空间中。例如，考虑相对论速度组合f(u, v) = u+v 1+uv。我们的构造相当深，因为我们假设u、v的乘法将使用两层(见图4.1(a))，1 + uv的倒数将使用一层，u + v和1/(1 + uv)的乘法将使用另外两层，总共5层。然而，自动发现的KAN只有2层深！事后看来，这实际上是可以预期的，如果我们回忆起相对论中的快速技巧：定义两个"快速"a ≡ arctanh u 和 b ≡ arctanh v。速度的相对论组合是在快速空间中简单的加法，即，u+v 1+uv = tanh(arctanh u + arctanh v)，这可以通过一个两层的KAN实现。

4. 讨论

这篇文章从数学基础、算法和应用的角度讨论了KAN的局限性和未来方向。

数学方面： 尽管我们已经对KAN进行了初步的数学分析，但我们对它们的数学理解仍然非常有限。科尔莫戈洛夫-阿诺德表示定理在数学上已经得到了深入研究，但该定理对应于形状为[n，2n + 1，1]的KAN，这是KAN的一个非常受限的子类。我们对更深层次的KAN的经验成功是否意味着数学上的一些基本内容？一个有吸引力的广义科尔莫戈洛夫-阿诺德定理可以定义"更深"的科尔莫戈洛夫-阿诺德表示，超越深度为2的组合，并且可能将激活函数的平滑性与深度相关联。假设地，存在一些函数，在原始的（深度为2的）科尔莫戈洛夫-阿诺德表示中不能平滑表示，但可能在深度为3或更深的情况下平滑表示。我们是否可以使用"科尔莫戈洛夫-阿诺德深度"的概念来刻画函数类别？

算法方面：我们讨论以下内容：

（1）准确性。在架构设计和训练中存在多种选择，尚未进行充分调查，因此替代方案有可能进一步提高准确性。例如，可以用径向基函数或其他局部核函数替换样条激活函数。可以使用自适应网格策略。

（2）效率。KAN运行缓慢的一个主要原因是不同的激活函数无法利用批量计算（通过相同函数处理大量数据）。实际上，可以通过将激活函数分组到多个组（"多头"）中来插值，从而在激活函数完全相同（MLPs）和完全不同（KANs）之间进行插值，在同一组内的成员共享相同的激活函数。

（3）KAN和MLP的混合。与MLP相比，KAN有两个主要区别：

（i）激活函数位于边而不是节点上，（ii）激活函数是可学习的而不是固定的。哪种变化更重要来解释KAN的优势？我们在附录B中展示了我们的初步结果，我们研究了一个具有（ii）的模型，即激活函数是可学习的（像KANs），但不是（i），即激活函数位于节点上（像MLP）。此外，也可以构建另一个模型，其激活是固定的（像MLP），但位于边上（像KAN）。

（4）适应性。由于样条基函数的固有局部性，我们可以在设计和训练KAN时引入适应性，以提高准确性和效率：参见多级训练的想法，如[93，94]中的多重网格方法，或者如[95]中的域相关基函数的多尺度方法。

应用方面： 我们提供了一些初步证据表明，在科学相关任务中，KAN比MLP更有效，例如拟合物理方程和PDE求解。我们期望KAN也可能对求解Navier-Stokes方程、密度泛函理论或任何可以阐述为回归或PDE求解的任务有所帮助。我们还希望将KAN应用于与机器学习相关的任务，这需要将KAN集成到当前的架构中，例如transformers - 有人可能会提出用KANs替换transformers中的MLPs的"kansformers"。KAN作为AI +科学的"语言模型"之所以如此变革性，是因为它们对任何能够使用自然语言的人都很有用。科学的语言是函数。KAN由可解释的函数组成，因此当人类用户盯着一个KAN时，就像用函数语言与它交流一样。本段旨在促进AI-科学家-协作范式，而不是我们特定的工具KANs。就像人们使用不同的语言交流一样，我们预期在未来KANs将只是AI +科学中的一种语言，尽管KANs将是使AI和人类沟通的第一种语言之一。然而，借助于KANs的启用，AI-科学家-协作范式从未如此简单和方便，这促使我们重新思考如何接近AI +科学的范式：我们想要AI科学家，还是想要能帮助科学家的AI？（完全自动化的）AI科学家的固有困难在于很难将人类偏好量化，这会将人类偏好编码成AI目标。事实上，不同领域的科学家可能对哪些函数简单或可解释有不同的看法。因此，对于科学家来说，拥有一种可以说科学语言（函数）并且可以方便地与个别科学家的归纳偏见进行互动以适应特定科学领域的AI更为可取。

最终的结论：我应该使用KAN还是MLP？

目前，KAN的最大瓶颈在于其训练速度慢。与MLP相比，给定相同数量的参数，KAN通常慢10倍。尽管我们没有努力优化KAN的效率，但我们认为KAN的训练速度慢更多地是未来需要改进的工程问题，而不是基本限制。如果想快速训练模型，则应使用MLP。然而，在其他情况下，KAN应该与MLP相当或更好，这使它们值得一试。简而言之，如果您关心可解释性和/或准确性，并且缓慢的训练不是主要问题，我们建议尝试KANs。

对更多实验结果和文章细节感兴趣的读者，可以阅读一下论文原文~

本文仅做学术分享，如有侵权，请联系删文。

3D视觉工坊交流群

目前我们已经建立了3D视觉方向多个社群，包括2D计算机视觉、大模型、工业3D视觉、SLAM、自动驾驶、三维重建、无人机等方向，细分群包括：

2D计算机视觉：图像分类/分割、目标/检测、医学影像、GAN、OCR、2D缺陷检测、遥感测绘、超分辨率、人脸检测、行为识别、模型量化剪枝、迁移学习、人体姿态估计等

大模型：NLP、CV、ASR、生成对抗大模型、强化学习大模型、对话大模型等

工业3D视觉：相机标定、立体匹配、三维点云、结构光、机械臂抓取、缺陷检测、6D位姿估计、相位偏折术、Halcon、摄影测量、阵列相机、光度立体视觉等。

SLAM：视觉SLAM、激光SLAM、语义SLAM、滤波算法、多传感器融合、多传感器标定、动态SLAM、MOT SLAM、NeRF SLAM、机器人导航等。

自动驾驶：深度估计、Transformer、毫米波|激光雷达|视觉摄像头传感器、多传感器标定、多传感器融合、自动驾驶综合群等、3D目标检测、路径规划、轨迹预测、3D点云分割、模型部署、车道线检测、Occupancy、目标跟踪等。

三维重建：3DGS、NeRF、多视图几何、OpenMVS、MVSNet、colmap、纹理贴图等

无人机：四旋翼建模、无人机飞控等

除了这些，还有求职、硬件选型、视觉产品落地、最新论文、3D视觉最新产品、3D视觉行业新闻等交流群

添加小助理: dddvision，备注：研究方向+学校/公司+昵称（如3D点云+清华+小草莓）, 拉你入群。

3D视觉工坊知识星球

3D视觉从入门到精通知识星球、国内成立最早、6000+成员交流学习。包括：星球视频课程近20门（价值超6000）、项目对接、3D视觉学习路线总结、最新顶会论文&代码、3D视觉行业最新模组、3D视觉优质源码汇总、书籍推荐、编程基础&学习工具、实战项目&作业、求职招聘&面经&面试题等等。欢迎加入3D视觉从入门到精通知识星球，一起学习进步。

3D视觉工坊官网：www.3dcver.com

3DGS、NeRF、结构光、相位偏折术、机械臂抓取、点云实战、Open3D、缺陷检测、BEV感知、Occupancy、Transformer、模型部署、3D目标检测、深度估计、多传感器标定、规划与控制、无人机仿真、三维视觉C++、三维视觉python、dToF、相机标定、ROS2、机器人控制规划、LeGo-LAOM、多模态融合SLAM、LOAM-SLAM、室内室外SLAM、VINS-Fusion、ORB-SLAM3、MVSNet三维重建、colmap、线面结构光、硬件结构光扫描仪，无人机等。

3D视觉相关硬件

—  完  —

点这里