如何理解动态规划

1. 动态规划

动态规划（Dynamic programming，简称 DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列，最小编辑距离等等。

动态规划常常适用于有重叠子问题和最优子结构性质的问题，并且记录所有子问题的结果，因此动态规划方法所耗时间往往远少于朴素解法。

动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归，自底向上就是递推。

使用动态规划解决的问题有个明显的特点，一旦一个子问题的求解得到结果，以后的计算过程就不会修改它，这样的特点叫做无后效性，求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次，具有天然剪枝的功能，从而减少计算量。

这是leetcode上面的概念，我们可以把他结构化一下，并理解一下具体的概念。

1、什么是最优子结构？

当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质。

可以反向理解，我们可以通过子问题的最优解，推导出问题的最优解，也就是子找父。如果我们把最优子结构，对应到我们前面定义的动态规划上，那我们也可以理解为，原问题可以通过子问题推导出来，如F(10) = F(9)+F(8)，则F(9)和F(8)是F(10)的最优子结构。

2、什么是重叠子问题？

递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次，这种性质称为子问题的重叠性质。

3、什么是无后效性？

某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响。

2. 斐波拉契数列

斐波那契数列指的是这样一个数列：

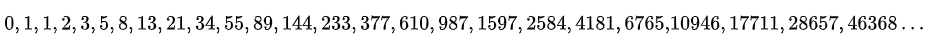
这个数列数列从第 3 项开始，每一项都等于前两项之和。其递推公式为：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
1
2

2.1 暴力递归

我们通过递归的方式来实现一个斐波那契数列

public int fib(int n) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    return fib(n - 1) + fib(n - 2);
}
1
2
3
4
5
6
7
8
9

可以看到在leetcode运行上并不是很优秀。

我们来分析一下它的执行过程，假如我们要求n=6的值，则其递归树如下：

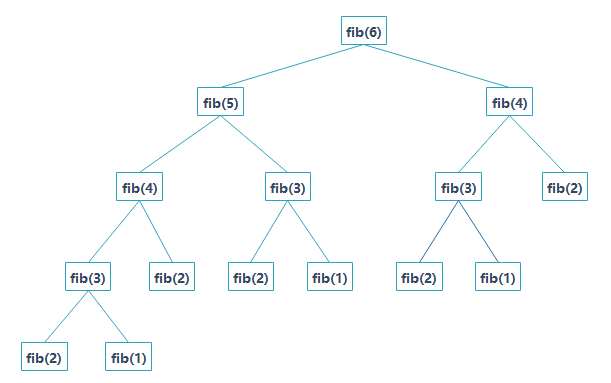
可以看到，上面每个节点都会执行一次，而且存在重复执行的节点，这也就是重叠子问题性质的表现，如fib(2)被重复执行了 5 次。由于调用每一个函数的时候都要保留上下文，所以空间上开销也不小。这么多的子节点被重复执行，如果在执行的时候把执行过的子节点保存起来，后面要用到的时候直接查表调用的话可以节约大量的时间。

我们试着用动态规划的自底向上和自顶向下方式来解决斐波拉契数列问题。

2.2 自顶向下备忘录

在递归方法中如果要计算原问题 f(20)的值，就得先计算出子问题 f(19) 和 f(18)，然后要计算 f(19)，我就要先算出子问题 f(18) 和 f(17)，以此类推。最后遇到 f(1) 或者 f(2) 的时候，结果已知，就能直接返回结果，递归树不再向下生长了。

因此，我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。

一般使用一个数组充当这个「备忘录」，当然也可以使用哈希表。

private Map<Integer, Integer> memo = new HashMap<>();
//备忘录法
public int fib(int n) {
    if (n == 0) return 0;
    if (n == 1 || n == 2) return 1;
    if (memo.containsKey(n)) {
        return memo.get(n);
    } else {
        int value = fib(n - 1) + fib(n - 2);
        memo.put(n, value);
        return value;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

再次查看时间消耗，很明显耗时减少。

「备忘录」到底做了什么？

当计算 f(20)的值，先计算出 f(19) 和 f(18)，而在计算f(19)的值时，已经把f(18)的值计算出来了。

实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数，即：

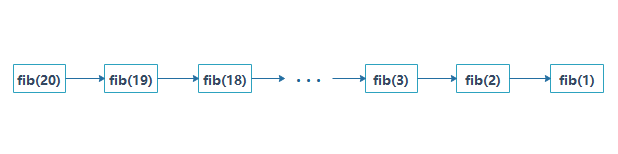
2.3 自底向上动态规划

可以看到，备忘录法还是利用了递归，计算fib(20)的时候还是要计算出fib(19)，fib(18)，fib(17)…，如果我们先计算出fib(1)，fib(2)，fib(3)…呢？这也就是动态规划的核心，先计算子问题，再由子问题计算父问题。

因为我们已经知道fib(0)和fib(1)的值，实际上，fib(2)的值也是知道的，即：

fib(2) = fib(0) + fib(1) = 1
fib(3) = fib(1) + fib(2) = 2
fib(4) = fib(2) + fib(3) = 3
fib(5) = fib(3) + fib(4) = 5
fib(6) = fib(4) + fib(5) = 8
......
1
2
3
4
5
6

我们根据备忘录的思想，用一张表来记录，即：

public int fib(int n) {
    if (n == 0) return 0;
    //dp表，n+1是因为0~n,有n+1个数
    int[] dp = new int[n + 1];
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}
1
2
3
4
5
6
7
8
9
10
11

看看实际效果：

另外，我们可以看到尽管用数组自底向上保存了先计算的值，但实际上参与循环计算的始终只有i,i-1,i-2这3项，即

因此，可以把上面的代码优化为：

public int fib(int n) {
    if (n == 0) return 0;
    if (n == 1 || n == 2) return 1;
    int a = 1;
    int b = 1;
    int temp = 0;//temp即为下一次循环的b的值
    for (int i = 3; i <= n; i++) {
        temp = a + b;
        a = b;
        b = temp;
    }
    return temp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

3. 动态规划基本设计步骤

当然，斐波拉契数列只是一个超级简单的动态规划的引子，也就是说刚入门，但是我们确可以从中得到一些启发，对于动态规划，无非就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。因此，我们可以总结出动态规划基本设计步骤：

1. 数组元素的含义，即dp[]，如自底向上的解法，dp[n]就代表第n项的值。
2. 数组元素之间的关系式（或者叫状态转移方程），当我们要计算 dp[n] 时，是可以利用 dp[n-1],dp[n-2]… dp[1]，来推出 dp[n] ，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，如 dp[n] = dp[n-1] + dp[n-2]，当然这个不同题意，关系式也不同，同时也是难点。
3. 初始值，也就是 dp 中的边界情况，我们通过公式dp[n] = dp[n-1] + dp[n-2]去递推，当递推到 dp[2] = dp[1] + dp[0]，此时dp[1] 和 dp[0] 不能再分解，因此我们必须要知道dp[1] 和 dp[0] 的值。

下面通过几个例子来实战一下。

3.1 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。有多少种不同的方法可以爬到楼顶？（n 为正整数）

我们按照上面的步骤来分析。

1、定义数组元素的含义

假设跳上一个 n 阶的台阶总共有dp(n)种跳法。

2、定义数组元素之间的关系式

把原问题拆分为子问题，因为每次可以爬 1 或 2 个台阶，因此：

第一层：1种,记为dp(1)=1,n=1

第二层：2种（走2步或走两个1步）,记为dp(2)=2,n=2

第三层：3种（走3个1步或在第一层走2步或在第二层走1步）,记为dp(3)=dp(1)+dp(2),n=3

......
1
2
3
4
5
6
7

因此第 n 层与第 n-1 和第 n-2 层有关。即到达第 n 级的台阶有两种方式：

• 一种是从第 n-1 级跳上来
• 一种是从第 n-2 级跳上来

即：dp[n] = dp[n-1] + dp[n-2]

很明显可以看出，其实就是一个斐波拉契数列，唯一的区别就是临界值不同，这里的 n 不能为 0。

3、初始值

在第二步就已经得到其初始值为dp(1)=1,dp(2)=2，需要注意的就是临界值。

代码实现

public int climbStairs(int n) {
    if (n <= 1) return 1;
    if (n == 2) return 2;
    int[] dp = new int[n + 1];
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}
1
2
3
4
5
6
7
8
9
10
11

3.2 不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？

还是按照上面的步骤来分析：

1、定义数组元素的含义

题目是求从左上角到右下角有多少种路径，如果用函数来表示则是：dp(i,j)，假设i,j的位置就是目标点，则其取值范围分别为[0,i)和[0,j)。也就是说当机器人从左上角走到(i,j) 这个位置时，一共有 dp[i][j] 种走法。（很自然的一个二维数组，假设i表示向右走，j表示向下走）

2、定义数组元素之间的关系式

因为机器人每次只能向下或者向右移动一步，假设目标点是(i,j)，则分两种情况：

• 向下走一步到达，那么上一步的位置则是(i-1,j)；
• 向右走一步到达，那么上一步的位置则是(i,j-1)。

因此，总共的走法则有：dp[i][j] = dp[i-1][j] + dp[i][j-1]

3、初始值

对于初始值，其实我们很好判定，如 i = 0或者j = 0（注：这里的0表示的数组下标），那么此时对于上面的表达式是不存在的，即为负数了，所以我们可以设置边界条件，如下：

• i = 0，表示横向只有一个格子，则只能一直往下走，很显然只有一条路径，dp[0][j] = 1；
• j = 0，表示纵向只有一个格子，则只能一直往右走，很显然也只有一条路径，dp[i][0] = 1；

代码实现

public int uniquePaths(int m, int n) {
   
    int[][] dp = new int[m][n];
    // 赋初始值
    for (int i = 0; i < m; i++) {
        dp[i][0] = 1;
    }
    for (int j = 0; j < n; j++) {
        dp[0][j] = 1;
    }
    // 从 1 开始
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    // 注意数组从 0 开始，所以要 -1
    return dp[m-1][n-1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

• 时间复杂度：O(m*n)
• 空间复杂度：O(m*n)

3.3 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。

注：子序列可以是不连续的，子字符串需要是连续的。

先分析一下，假如现在有字符串如下：

text1 = abfeghac

text2 = cabfeghc
1
2
3

1、定义数组元素的含义

还是老样子，2 个字符串，对应 2 个二维数组，思路如下：

1. 把两个字符串分别以行和列组成一个二维的矩阵；
2. 比较二维矩阵中每个点对应行列字符中否相等，相等的话值设置为 1，否则设置为 0；
3. 通过查找出值为1的最长对角线就能找到最长公共子串。

从上图可以看出，有 4 个公共子串，且最长公共子串为 7，abfeghc（为什么是 7 ，注意上面对子序列的描述）。

但这存在一个问题，我们还得再去计算这个公共子串的长度，因此我们在计算这个二维矩阵的时候顺带着计算出这个子串的长度，用i、j表示两个子串的长度， dp[i][j]表示其公共长度，如下：

dp[i][j] ，其含义是在 text1[0,i-1] 与 text2[0,j-1] 之间匹配得到的想要的结果。

注：i、j表示两个数组的长度，所以定义的数组范围是0 ~ i-1，因此i-1表示最后一位字符，j同理。

2、定义数组元素之间的关系式

从上图中我们可以看出，存在两种情况，即 2 个字符串存在相等的字符：

• 当text1[i-1] == text2[j-1]时，说明两个字符串最后一位有相等的字符，所以公共子序列+1，即dp[i][j] = dp[i-1][j-1]+1。

• 当text1[i-1] != text2[j-1]时，说明两个字符串最后一位没有相等的字符，最后一个元素不相等，那说明最后一个元素不可能是最长公共子序列中的元素，此时存在 2 种情况，dp[i-1][j]和dp[i][j-1]，其中：

  • dp[i-1][j]：表示最长公共序列可以在1,2,3,...,i-1和 1,2,3,...,j中找。
  • dp[i][j-1]：表示最长公共序列可以在1,2,3,...,i和 1,2,3,...,j-1中找。

  求解上面两个子问题，得到的公共子序列谁最长，谁就是最长子序列，即dp[i][j] = max(dp[i−1][j],dp[i][j−1])。

综上，状态转移方程为：
d p [ i ] [ j ] = { d p [ i − 1 ] [ j − 1 ] + 1 , t e x t 1 [ i − 1 ] = t e x t 2 [ j − 1 ] m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) , t e x t 1 [ i − 1 ] ≠ t e x t 2 [ j − 1 ] dp[i][j] =

$$\begin{cases} dp[i-1][j-1]+1, & text_1[i-1] = text_2[j-1] \\ \\ max(dp[i-1][j],dp[i][j-1]), & text_1[i-1] \neq text_2[j-1] \end{cases}$$ dp[i][j]=⎩⎪⎨⎪⎧​dp[i−1][j−1]+1,max(dp[i−1][j],dp[i][j−1]),​text1​[i−1]=text2​[j−1]text1​[i−1]​=text2​[j−1]​
3、初始值

当i=0或者j=0时，即是空串和字符串来比较，结果肯定为 0 ，即dp[0][j]=0 ，dp[i][0]=0。

由于 dp[i][j] 依赖与 dp[i-1][j-1] , dp[i-1][j], dp[i][j-1]，所以 i 和 j的遍历顺序肯定是从小到大的。

另外，由于当 i和 j 取值为 0 的时候，dp[i][j] = 0，而 dp 数组本身初始化就是为 0，所以，直接让 i 和 j从 1 开始遍历。遍历的结束应该是字符串的长度。

代码实现

public int longestCommonSubsequence(String text1, String text2) {
    int m = text1.length();
    int n = text2.length();
    int[][] dp = new int[m + 1][n + 1];
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4. 总结

实际上动态规划的问题主要就是掌握其性质，最优子结构和重叠子问题，即把大的问题拆分为一个个小的问题，在按照上面的几个步骤来解决问题。

当然，练习是必不可少的，熟能生巧。

5. 参考

• https://hollis.blog.csdn.net/article/details/103045322
• https://blog.csdn.net/u010397369/article/details/38979077