力扣 238.除自身以外数组的乘积

题目描述：

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

示例 2:

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

提示：

• 2 <= nums.length <= 105
• -30 <= nums[i] <= 30
• 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内

注意：改到题目要求不能使用乘法，但是也实现了使用乘法的代码，但是由于题目禁止使用，这里就作为一个参考，不作详细说明

代码实现：

public static int[] productExceptSelf(int[] nums) {
        long res = 1;
        int count_zero = 0;
        int index = 0;
        for (int i = 0; i < nums.length; i++) {
            //System.out.println("nums[i]: "+nums[i]);
            if (nums[i] == 0) {
                ++count_zero;
                if (count_zero == 2) {
                    res = 0;
                    break;
                } else {
                    index = i;//说明index出需要置为res，其余位置置为0
                }
            } else {
                res *= nums[i];
            }
 
        }
        int[] a = new int[nums.length];
        if (count_zero == 2) {
            Arrays.fill(a, 0);
        } else if (count_zero == 1) {
            a[index] = (int) res;
        } else {
            for (int i = 0; i < nums.length; i++) {
                a[i] = (int) res / nums[i];
            }
        }
        return a;
    }

正经题解：

因为只能使用乘法，但是暴力方法会产生很多不必要的重复计算，因此需要改进乘法计算过程。

首先考虑正常情况下计算除去i位置之外数组元素乘积要怎么计算，无非就是将i位置元素置为1，然后将剩余的全部元素乘起来；

但是如果现在存在某一个位置是0(仅有一个位置元素是0)，那么ans[i]还是可以通过将i位置元素置为1，然后将其他位置元素乘起来得到；

如果现在有多个0，计算ans[i]的时候还是可以将i位置元素置为1，将其他位置元素乘起来的到。

基于上述考虑，计算ans[i]的时候，将i位置元素置为1，计算其他位置元素乘积的方法可行。

接下来考虑出去重复计算的方法，比如现在数组大小是7，计算ans[3]的时候，完整计算表达式:

nums[0]*nums[1]*nums[2]*1*nums[4]*nums[5]*nums[6]

计算ans[3]的时候完整的表达式是：

nums[0]*nums[1]*nums[2]*nums[3]*1*nums[5]*nums[6]

不难发现，计算ans[3]的时候计算的nums[0]*nums[1]*nums[2]，在计算ans[4]的时候其实不用算，只要在上次计算出来的nums[0]*nums[1]*nums[2]基础上乘以nums[3]即可形成ans[4]中 “1”之前的完整表达式的值；

同理，“1”之后也有一样的规律，计算出来ans[4]的nums[5]*nums[6]之后 再去计算ans[3]的"1"之后的表达式的值时候，就只需要在ans[4]计算出来的nums[5]*nums[6]基础上再乘上nums[4]。

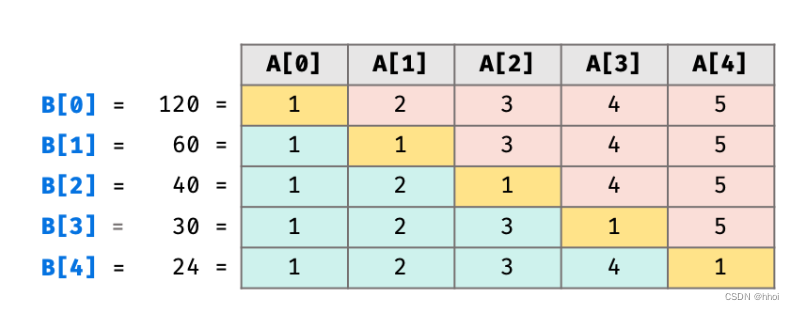
现在需要考虑怎样将1之前计算出来的值保存起来，供下一个ans使用。对于前半部分来说，就用ans来保存重复部分就好，比如计算出来ans[1] 的前半部分乘积：ans[1] = nums[0]之后，ans[2]的前半部分就等于：ans[2] = ans[1] * nums[1] 以此类推，得出前半段计算代码：

for (int i = 1; i < len; i++) {
            ans[i] = ans[i - 1] * nums[i - 1];
        }

后半段计算同理，但是注意需要一个temp来存储重复的部分，以供下一个ans后半段的计算：

for (int i = len - 2; i >= 0; i--) {
            temp *= nums[i+1];
            ans[i] *= temp;
        }

完整的代码实现：

public static int[] productExceptSelf2(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return new int[0];
        }
        int[] ans = new int[len];
        ans[0] = 1;
        int temp = 1;
        //计算下三角
        for (int i = 1; i < len; i++) {
            ans[i] = ans[i - 1] * nums[i - 1];
        }
        //计算上三角
        for (int i = len - 2; i >= 0; i--) {
            temp *= nums[i+1];
            ans[i] *= temp;
        }
        return ans;
    }

参考来源：

作者：Krahets
链接：https://leetcode.cn/problems/product-of-array-except-self/solutions/11472/product-of-array-except-self-shang-san-jiao-xia-sa/
来源：力扣（LeetCode）