- 1修复 MySQL 数据库的终极指南
- 2关于前后端分离框架的一些疑问
- 3300分钟吃透分布式缓存-15讲:如何深入理解、应用及扩展 Twemproxy?
- 4医院信息系统_医院信息系统csdn
- 5入门Uni-app开发:构建跨平台应用的全能利器_uni-app跨平台开发与应用
- 6计算机视觉实验:直方图均衡化、Hough变化应用
- 7Python(13):常见的4种设计模式(单例,工厂,策略,观察者)_python 设计模式
- 8网络安全测试中的跨站点脚本攻击(XSS):Python和FlaskSecurity实现跨站脚本攻击测试_flask-security
- 9BeautifulSoup4认识与应用
- 10解密 MobaXterm 已经存储 Session 账号的密码_mobaxterm密码
最优化方法——最小二乘法与梯度下降法_梯度下降法求解x-2)^4+(x-2*y)^2
赞
踩
目录
系列文章目录
本系列博客重点在最优化方法的概念原理与代码实践(有问题欢迎在评论区讨论指出,或直接私信联系我)。
代码可以全抄 大家搞懂原理与流程去复现才是有意义的!!!
第一章 最优化方法——K-means实现手写数字图像聚类_@李忆如的博客-CSDN博客
第二章 最优化方法——QR分解_@李忆如的博客-CSDN博客
第三章 最优化方法——最小二乘法
梗概
本篇博客主要介绍最小二乘法、梯度下降法的原理与流程,分别使用Matlab、Pycharm分别实现了最小二乘法、不同迭代停止条件的梯度下降法等方法对给定优化模型进行求解并进行解之间的误差分析对比,并进行了一定理论与应用(内附数据集和python及matlab代码)。
一、问题
读取附件“MatrixA_b.mat”文件中的矩阵A和向量b。建立关于矩阵, 向量,未知向量最小二乘优化模型:
2)利用梯度下降法迭代求出模型“近似解”,通过设置迭代停止条件,分析“近似解”与“准确解”之间的误差。
二、实验思路综述
1.实验工具及算法
本次实验分别使用Matlab、Pycharm分别实现了最小二乘法、不同迭代停止条件的梯度下降法等方法对给定优化模型进行求解并进行解之间的误差分析对比。
2.实验数据
本次实验使用给定矩阵A(50x40)与向量b(50x1)组成的优化模型进行实验内容的探究,在拓展内容的探究与尝试中使用了部分网络数据集。
3.实验目标
本次实验要求使用不同方法对给定优化模型(最小二乘问题)进行求解并进行解的误差分析及对比。此外,本人还在相关理论方面进行了补充,对算法应用进行了实践。
4.实验步骤
本次实验大致流程如表1所示:
表1 实验3流程
| 1.实验思路综述 |
| 2.最小二乘问题的引入 |
| 3. 最小二乘法的推导与求解 |
| 4. 梯度下降法的推导与求解 |
| 5. 不同情况解的分析及误差对比 |
| 6. 理论拓展与应用实践 |
三、最小二乘问题引入
1.最小二乘问题样例
在求解最小二乘问题前,我们需要对其进行定义与数学模型化,故本部分引入一个二维样例如图1所示,一个实际的测量问题如图2所示:
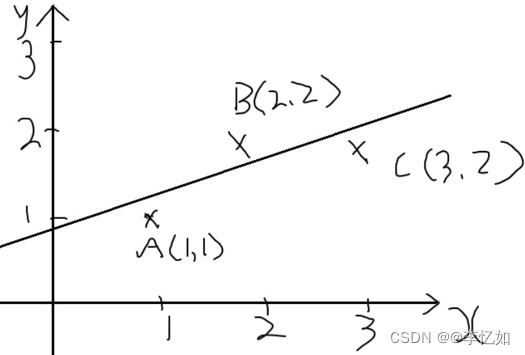
图1 二维最小二乘问题样例

图2 实际最小二乘问题样例
分析:对于图1的问题,无法找到一条直线同时经过A、B、C三点,对于图2的问题,我们无法求解出一组满足条件的x1,x2,x3。
2.最小二乘问题解决方案及数学模型化
最小二乘问题:由于各种误差,难以求得满足问题条件的一组解(无法通过现有数据拟合出一条过所有数据的线或超平面)的问题。
解决方案:对于最小二乘法,核心的解决方案就是寻找该问题的近似解。并尽可能逼近原问题的目标,使残差向量r=Ax-b在某种度量下尽可能小。最小二乘问题数学模型化如图3所示:

图3 最小二乘问题模型
3.相关线性代数知识导入
在后续需要用不同方法求解最小二乘问题,在此对核心相关线性代数知识进行一定补充。
3.1 梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
梯度求解样例如式1所示:
式1 梯度求解样例
3.2 矩阵的逆
当一个矩阵X满足XA=I时,X被称为A的左逆,同理可以定义右逆。
矩阵的逆:如果矩阵A存在左逆和右逆,则左逆和右逆一定相等,此时X称为矩阵的逆(矩阵非奇异),记作A^-1。
逆存在的判断:对于一个矩阵的逆是否存在,有如表2中所示五种常用方法:
表2 逆矩阵存在判断常用方法
| 1.若矩阵行列式不为0,可逆 |
| 2.若矩阵的秩为n,可逆 |
| 3.若存在一个矩阵B,使AB=BA=I,可逆 |
| 4.对于齐次方程AX=0,若方程只有零解,可逆 |
| 5.对于非齐次线性方程AX=b,若方程只有特解,可逆 |
矩阵逆的常用证明框架如图4所示:

图4 矩阵逆的证明框架
补充:性质(a)对任意矩阵A都成立,性质(b)对方阵矩阵A都成立。
逆矩阵求解:在编程实现中矩阵求逆一般使用库函数,在不同语言中均进行了打包,如matlab中可使用inv()求逆矩阵,用法详见:矩阵求逆 - MATLAB inv - MathWorks 中国,用pinv()求伪逆,用法详见:Moore-Penrose 伪逆 - MATLAB pinv - MathWorks 中国
3.3 QR分解
QR分解是将一个矩阵A分解成具有标准正交列向量的矩阵Q和上三角矩阵R(对角线元素不为0)的算法。这个分解能够有效的提高计算机求解线性方程、最小二乘问题、带约束的最小二乘问题的效率,有效降低计算复杂度,QR分解形式如图5所示。

图5 QR分解定义形式
QR分解根据原理分为Gram-Schmidt、Householder、Givens三种实现方法,经本人实验2探究发现,对于较稠密矩阵,使用Householder QR分解有较高的效率与稳定性。
四、最小二乘法
在本部分对于最小二乘法的定义、数学模型化、目标求解推导、模型求解做详解。
1.定义
最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合,其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域也得到广泛应用。
2.数学模型化
2.1 目标函数
结合最小二乘问题模型与最小二乘法定义,将最小二乘法数学模型化,故对于给定的给定A∈R^mxn,b∈R^m,求解x∈R^n让目标函数最小,目标函数如式2所示:
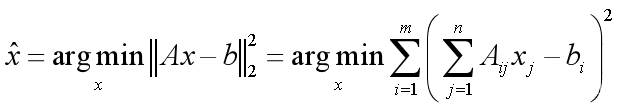
式2 最小二乘法目标函数
2.2 最小二乘法的解
结合最小二乘法的原理,对于式2的目标函数求解,得到的x应该满足式3的条件:

式3 最小二乘法的解的条件
分析:当残差r=Ax−b=0时,则x是线性方程组Ax=b的解;否则其为误差最小平方和下方程组的近似解。
2.3 列向量空间的意义
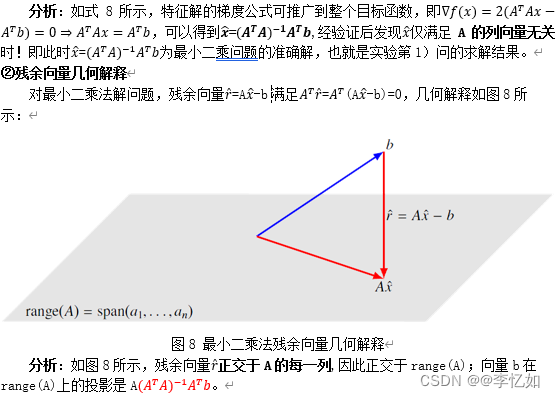
对于满足最小二乘法目标函数式2的解x,其列向量空间的意义如图6所示:

图6 最小二乘法列向量空间的意义
分析:如图6所示,Ax∈range(A)中最接近b的向量,r=Ax-b正交(垂直)于值域空间range(A)。
3.目标求解推导
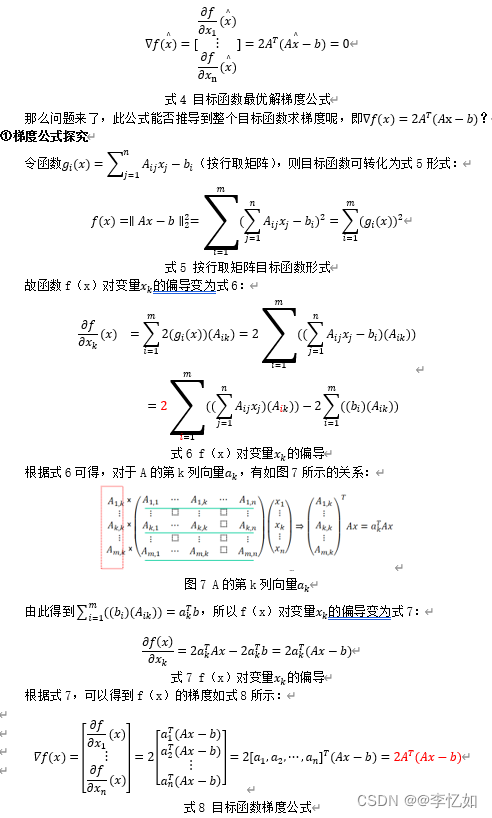
对于最小二乘法的目标函数式2,我们需要得到满足式3条件的最优解x。由于目标函数f(x)为可微函数,故最优解x满足梯度∇f(x)=0,如式4所示:
4.正规方程
由最小二乘法定义与梯度公式求导可知,我们需要找到目标函数的最优解即找梯度∇f(x)=0,梯度公式推导后如式8所示,由此定义最小二乘法的正规方程如式9所示:
式9 最小二乘法正规方程
分析:分析式9中的正规方程,其等价于∇f(x)=0,f(x)=,且最小二乘法问题所有解都满足正规方程。如果A的列线性无关,则A^TA为非奇异矩阵,此时正规方程(原问题)有唯一解。
对于正规方程的求解一般有三种方法,分别为直接求解正规方程组求解、通过Gram矩阵求解与QR分解求解,后两种方法实现流程详解如下:
4.1 通过Gram矩阵求解正规方程
通过Gram矩阵求解正规方程一般流程如表3所示:

Tips:经过四舍五入之后,Gram矩阵为奇异矩阵。
4.2 通过QR分解求解正规方程
方法②比方法①更稳定,因为它避免构造Gram矩阵,通过QR分解求解正规方程一般流程如表4所示:

5.编程实践
根据实验任务1)的要求,本部分将编程实践通过最小二乘法的正规方程,求出给定数据优化模型的准确解。
5.1 QR分解
对实验给定矩阵A与向量b进行导入,并对A进行QR分解(Householder),算法流程如表5所示:

在代码实现上,可使用matlab库函数[Q,R] = qr(A)使用Householder进行QR分解,用法解析可见:QR 分解 - MATLAB qr - MathWorks 中国,也可自己构建QR分解函数,分解与稳定性分析代码可见:最优化方法——QR分解_@李忆如的博客-CSDN博客
5.2 求最优解
在得到给定矩阵A分解出的Q、R矩阵(不同QR分解得到不同矩阵,需要转换)后,根据公式10对Q、R、b进行求最优解并编程实现(逆矩阵可用inv()函数求),最终得到最优解x_least并保存供后续对比,代码如下:
x_least=inv(R)*Q'*b; %精确解五、梯度下降法
除了最小二乘法,梯度下降法也常用于最优化问题最优解的逼近,尤其是对于R^mxn列向量线性相关或n非常大的情况,本部分对于梯度下降法法的定义、数学模型化、目标求解推导、模型求解做详解。
1.定义
梯度下降法是一个一阶最优化算法。要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。即梯度下降法求解目标问题最优解的过程为:x1,x2,…,xk→x,其中xk是第k步迭代,期望更新xk+1,满足f(xk+1)<f(xk),核心原理如图12所示:
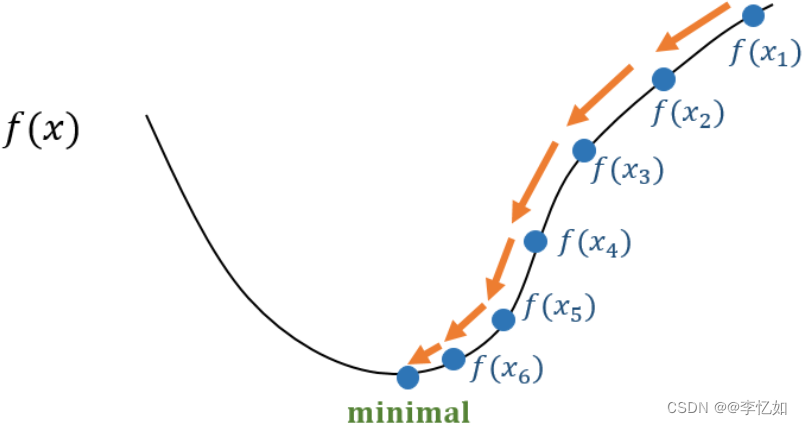
图12 梯度下降法核心原理
2.目标函数推导

3.操作与算法流程
对于优化问题,根据梯度下降法原理与目标求解推导总结其算法流程如表6所示:

其中,迭代停止条件一般有设置迭代次数与相邻迭代解之间的“相对接近程度”两种。
4.编程实践
根据实验任务2)的要求,本部分将编程实践通过梯度下降法求出给定优化模型的“近似解”,核心代码如下:
- %%梯度下降法
- min=0.01;
- x=zeros(40,1);
- for k = 1:30 %或指定迭代次数
- f(1,k)=0.5*norm(A*x-b,2)^2; % 目标函数值
- p = A'*(A*x-b);
- a = norm(p,2)^2 / norm(A*p,2)^2;
- y = x - a * p; %y为x(k+1)
- temp(1,k) = norm((x-y),2)/norm(x,2); %迭代解间的相对接近程度
- error(1,k) = norm((x_least - x),2); %误差迭代
- %
- % if norm((x-y),2)/norm(x,2) < min
- % break
- % end
- x = y; %迭代
- end

4.1 迭代次数
本部分以迭代次数作为迭代停止条件,为探究最优迭代次数,应观察分析不同迭代次数对于目标求解的影响(目标函数值的变化)。本次实验中,迭代次数与目标函数值之间的关系如图14所示:
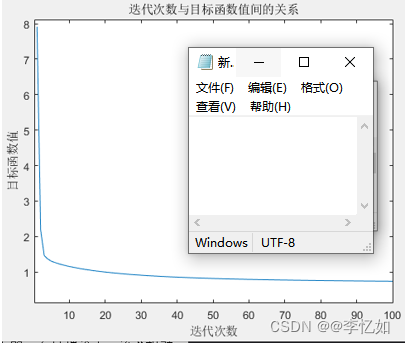
图14 迭代次数与目标函数值间的关系
分析:由图14可见,迭代次数在30之后,随迭代次数增大,目标函数趋于稳定,故在本实验中,选取迭代次数为30作为停止条件为较优选择。
4.2 相邻迭代解之间的“相对接近程度”
本部分以相邻迭代解之间的“相对接近程度”作为迭代停止条件,本实验以公式:为例作为评估标准。为探究最优阈值,应观察分析不同阈值对于目标求解的影响(目标函数值的变化)。本次实验中,迭代次数与相邻迭代解之间的“相对接近程度”之间的关系如图15所示:
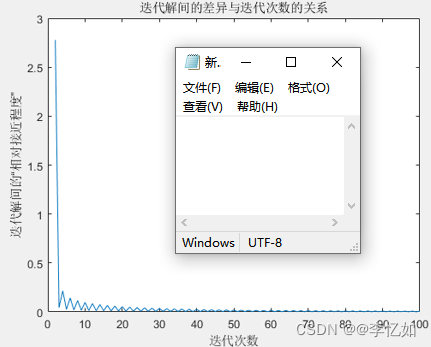
图15 迭代次数与相邻迭代解之间的“相对接近程度”之间的关系
分析:结合图14,由图15可见,随迭代次数增加,相邻迭代解之间的“相对接近程度”波动下降。经统计分析后,对本实验,我选择相邻迭代解之间的“相对接近程度”的阈值为0.01,作为梯度下降法的终止条件。
5.不同情况解的分析及误差对比
不同方法、语言求解最小二乘问题得到结果、效率都有所不同,本部分进行对比分析。
5.1 不同算法分析
最小二乘法与梯度下降法得到的解及对应效率是不同的,结合两种算法的原理与流程分析可做解释。
对于最小二乘法,核心就是求偏导,然后使偏导为0,得到理论上的“准确解”。其最后一步解方程组,计算量相对较大。
而对于梯度下降法,可以看作是更简单的一种求最小二乘法最后一步解方程的方法,本质上是在以梯度的方向和步长向目标“准确解”迭代逼近的算法。误差存在于梯度下降会有一个初始解,这个解往往与“准确解”的距离较远,所以每一次迭代的步长的方向和长度都是尽量“减小”误差,但是得到最后的解还是会与“准确解”存在一定的误差。
总的来说,最小二乘法可以得到全局最优的闭式解,梯度下降法是通过迭代更新来逐步进行的参数优化方法,最终结果为局部最优。
5.2 误差分析
本部分对两种不同迭代停止条件的梯度下降法求出的“近似解”与最小二乘法得到的“准确解”进行对比,然后用做误差分析。其中,迭代解与准确解的误差如图16所示,近似解与准确解之间的误差如表7所示:

图16 迭代解与准确解的误差关系
分析:由图16可见,初始化x(0)=0,以度量误差的情况下,梯度下降法求得的迭代解与最小二乘法求出的准确解之间的误差随迭代次数增加而减少,由0次迭代时误差为2.0007,到100次迭代时误差降为0.752。
表7 本实验近似解与准确解之间的误差

分析:由表7可见,初始化x(0)=0,以度量误差的情况下,本实验使用的两种梯度下降法(迭代次数=30停止,
<0.01停止)得到的近似解与最小二乘法得到的精确解(闭式最优)的误差分别为1.33798527与1.491785332。而两种梯度下降法得到的目标函数值与最小二乘法得到的函数值误差分别为0.084586155与0.1191079252。
5.3 效率对比
为探究不同方法的效率对比,本部分用上述提到的三种方法分别针对实验给定的最小二乘问题求解,每种方法运行20次,运行时间数据汇总如表8所示,效率对比如图17所示:
表8 不同方法求解最小二乘问题平均运行时间汇总
![]()
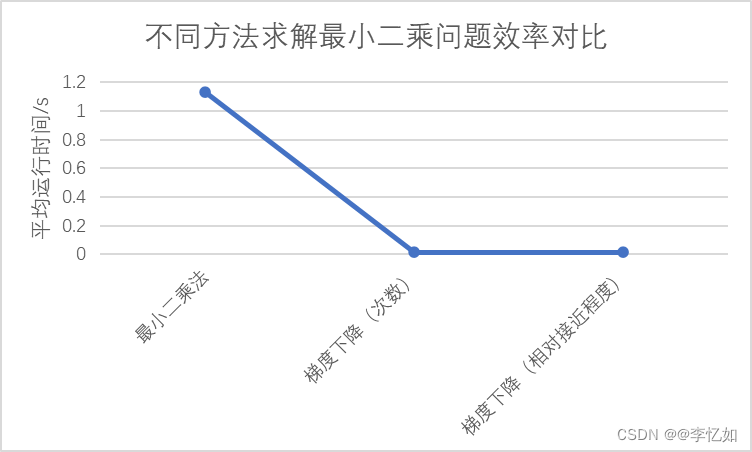
图17 不同方法求解最小二乘问题效率对比
分析:由表8与图17可见,无论是哪种梯度下降法,平均运行时间均低于最小二乘法。
结合正确性与效率分析,最小二乘法虽然能求出相对准确的解,但需要更长的运行时间,故在面对给定的问题时,应该有选择性的根据问题的性质选择两种方法中的一个。
具体来说,最小二乘法中需要计算矩阵的逆,这是相当耗费时间的,而且求逆也会存在数值不稳定的情况,因而这样的计算方法在应用中有时不值得提倡。
相比之下,梯度下降法虽然有一些弊端,迭代的次数可能也比较高,但是相对来说计算量并不大.而且,在最小二乘法这个问题上,收敛性有保证。故在大数据量的时候,反而是梯度下降法(其实应该是其他一些更好的迭代方法)更加值得被使用。
6.不同语言与平台对求解的影响
为探究不同语言与平台对最小二乘问题求解的影响,分别将最小二乘法、两种梯度下降法在Pycharm2021中使用Python重构,具体代码详见附件。
分别使用maatlab与python实现的三种方法对实验给定矩阵A(50x40)与向量b(50x1)进行求解,每个平台的各个方法均进行20次求平均运行时间,数据汇总如表8所示,效果对比如图18所示:
表8 不同语言、不同方法求解最小二乘问题的平均运行时间

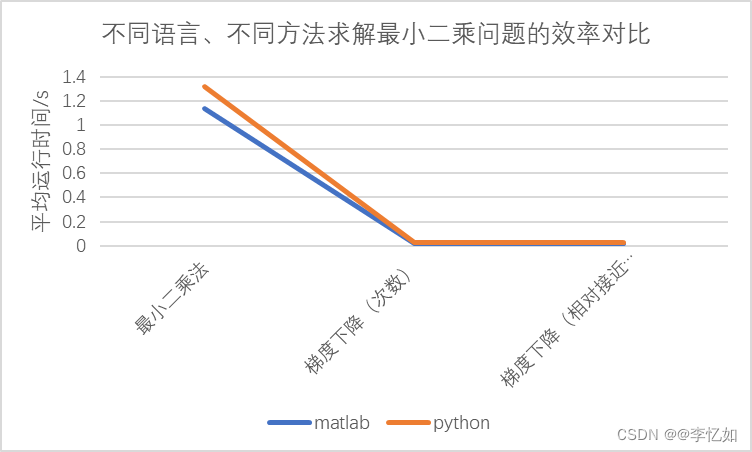
图18 不同语言、不同方法求解最小二乘问题的效率对比
分析:由表8与图18可见,在不同方法求解最小二乘问题中,matlab的运行时间均略低于Python,效率较高。
六、理论补充与应用拓展
对于最小二乘法与梯度下降法,除了本实验中对于矩阵向量构成的优化模型求解,在其他方面上也有广泛的应用,在本部分做简单尝试与实践。
1.最小二乘法
1.1 线性回归定义与算法步骤
线性回归及其详细应用可见:机器学习——LR(线性回归)、LRC(线性回归分类)与人脸识别
回归与线性回归:回归分析是指一种预测性的建模技术,主要是研究自变量和因变量的关系。线性回归为最基础的一种回归算法。用线(面)等模型对于现有相对线性的数据进行较小损失的拟合,并使拟合出的模型可较好预测数据,一般算法流程如表9所示:
表9 线性回归算法流程
| 输入: 数据集 |
| 过程: |
| 1、变量的筛选与控制 |
| 2、对正态性分布的数据做散点图与相关分析 |
| 3、通过最小化损失函数来确定参数,得到(拟合)回归方程 |
| 4、不断检验模型,优化参数,得到最优的回归方程 |
| 5、使用回归方程做预测 |
| 输出:回归方程 |
1.2 最小二乘法的应用
根据线性回归定义与表9所示,在线性回归问题中,常常使用最小二乘法来拟合数据,包括但不限于基于正规方程的解去拟合直线或超平面,预测数据。在本部分以一个实际样例探究最小二乘法在线性回归中的应用。
问题描述:探究学生成绩与学生学习时间的关系
线性回归实现:将学习时间作为变量,成绩作为预测值,建立回归方程,并用最小二乘法最小化损失函数,得到回归方程并验证,验证后用其预测。核心代码如下:
- %%最小二乘法应用
- x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
- y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];
- figure
- plot(x,y,'r*') %作散点图(制定横纵坐标)
- xlabel('x(学生学习时间)','fontsize',12)
- ylabel('y(学生成绩)','fontsize',12)
- set(gca,'linewidth',2)
- %采用最小二乘拟合
- Lxx=sum((x-mean(x)).^2);
- Lxy=sum((x-mean(x)).*(y-mean(y)));
- b1=Lxy/Lxx;
- b0=mean(y)-b1*mean(x);
- y1=b1*x+b0; %线性方程用于预测和拟合
- hold on
- plot(x,y1,'linewidth',2);
- m2=LinearModel.fit(x,y); %函数进行线性回归

数据与拟合结果如图20所示:

图20 数据与拟合结果
分析:由图20可见,可看出模型对数据拟合较好,预测相对线性。如需预测不在图中的数据,只需将对应学习时间作为x代入回归模型(方程)中即可。验证了最小二乘法在线性回归应用中的正确性。
2.梯度下降法
2.1 BP神经网络
BP神经网络及其应用详见:机器学习——深度神经网络实践(FCN、CNN、BP
BP神经网络是一种简单的神经网络,核心思路是模仿人的大脑工作原理,构造的一个数学模型,它的仿生结构如图21所示:

图21 BP神经网络拓扑图
其中,BP神经网络的结构包含三层,最靠前的是输入层,中间是隐层(可以有多个隐层,每层隐层可以有多个神经元),最后是输出层,一般工作流程如表10所示:
表10 BP神经网络流程
| 输入: 数据集 |
| 过程: |
| 1.输入层负责接收输入,在输入层接收到输入后,每个输入神经元会把值加权传递到各个隐层神经元。 |
| 2.各个隐神经元接收到输入神经元传递过来的值后,与自身的基础阈值b汇总求和,经过一个激活函数(通常激活函数是tansig函数),然后加权传给输出层。 |
| 3.输出神经元把各个隐神经元传过来的值与自身阈值b求和(求和后也可以再经过一层转换),即是输出值。 |
| 输出:对应结果 |
2.2 梯度下降法的应用
根据神经网络定义与表10所示,对于相关算法,参数更新是重要步骤。对于BP神经网络而言,常用梯度下降法去更新参数,即通过反向传播计算不同参数的梯度,再用梯度进行参数的优化。在本部分以一个实际样例探究梯度下降在BP神经网络中的应用。
问题描述:鸢尾花数据的分类(根据鸢尾花的四种特征属性去分三类)
BP神经网络实现:本次实践我选择了四层BP神经网络,第一层为输入层,第二层和第三层都为中间层,第四层为输出层。
输入层为四个神经元(每类特征属性都能参与计算),输出层为三个神经元(分别对应三个类别的概率大小),两个中间层根据经验确定为二十五个神经元。
将不同层神经元进行全链接,中间的链接即为权重w,除了输入层,其它层神经元都赋予一个偏置b以及激活函数f,另外给最后输出结果一个评判误差的损失函数。
权重w和偏置b通过随机数生成,中间层激活函数设置为relu函数,输出层激活函数设置为softmax函数(用来分类),损失函数设置为交叉熵误差(因为分类时用到了独热编码,因此适合用交叉熵误差)。
参数更新的方法设置为随机梯度下降法。即通过反向传播计算不同参数的梯度,再用梯度进行参数的优化。代码如下:
- # 训练集:鸢尾花150*50%
- # 网络结构:输入层(4)+中间层(25)+中间层(25)+输出层(3)
- # 中间层激活函数:relu,输出层激活函数:softmax
- # 损失函数:交叉熵误差
- # 随机梯度下降
-
- import numpy as np
- import matplotlib.pyplot as plt
- from sklearn import datasets
-
- # 鸢尾花数据读入
- iris_data = datasets.load_iris()
- input_data = iris_data.data
- correct = iris_data.target
- n_data = len(correct)
-
- # 对数据进行预处理
- # 标准化
- ave_input = np.average(input_data, axis=0)
- std_input = np.std(input_data, axis=0)
- input_data = (input_data - ave_input) / std_input
- print(input_data)
-
- # 标签转化为独热编码
- correct_data = np.zeros((n_data, 3))
- for i in range(n_data):
- correct_data[i, correct[i]] = 1.0
- print(correct_data)
- # 切分训练集和测试集
- index = np.arange(n_data)
- index_train = index[index % 2 == 0]
- index_test = index[index % 2 != 0]
-
- input_train = input_data[index_train, :]
- input_test = input_data[index_test, :]
-
- correct_train = correct_data[index_train, :]
- corre_test = correct_data[index_test, :]
-
- n_train = input_train.shape[0]
- n_test = input_test.shape[0]
-
- # 设置参数
- n_in = 4
- n_mid = 10
- n_out = 3
-
- wb_width = 0.1
- eta = 0.1
- epoch = 100
-
- batch_size = 8
- interval = 100
-
-
- # 实现网络层
- class Baselayer:
- def __init__(self, n_upper, n):
- self.w = wb_width * np.random.randn(n_upper, n)
- self.b = wb_width * np.random.randn(n)
-
- def updata(self, eta):
- self.w = self.w - eta * self.grad_w
- self.b = self.b - eta * self.grad_b
-
-
- class MiddleLayer(Baselayer):
- def forward(self, x):
- self.x = x
- self.u = np.dot(x, self.w) + self.b
- self.y = np.where(self.u <= 0, 0, self.u) # relu函数
-
- def backward(self, grad_y):
- delta = grad_y * np.where(self.u <= 0, 0, 1.0) # relu函数的求导--!!
- self.grad_w = np.dot(self.x.T, delta)
- self.grad_b = np.sum(delta, axis=0)
- self.grad_x = np.dot(delta, self.w.T)
-
-
- class OutputLayer(Baselayer):
- def forward(self, x):
- self.x = x
- u = np.dot(x, self.w) + self.b
- self.y = np.exp(u) / np.sum(np.exp(u), axis=1, keepdims=True) # SoftMax函数
-
- def backward(self, t):
- delta = self.y - t
- self.grad_w = np.dot(self.x.T, delta)
- self.grad_b = np.sum(delta, axis=0)
- self.grad_x = np.dot(delta, self.w.T)
-
-
- # 实例化
- middle_layer_1 = MiddleLayer(n_in, n_mid)
- middle_layer_2 = MiddleLayer(n_mid, n_mid)
- output_layer = OutputLayer(n_mid, n_out)
-
-
- # 定义函数
- def forward_propagation(x):
- middle_layer_1.forward(x)
- middle_layer_2.forward(middle_layer_1.y)
- output_layer.forward(middle_layer_2.y)
-
-
- def back_propagation(t):
- output_layer.backward(t)
- middle_layer_2.backward(output_layer.grad_x)
- middle_layer_1.backward(middle_layer_2.grad_x)
-
-
- def update_wb():
- middle_layer_1.updata(eta)
- middle_layer_2.updata(eta)
- output_layer.updata(eta)
-
-
- def get_error(t, batch_size):
- return -np.sum(t * np.log(output_layer.y + 1e-7)) / batch_size
-
-
- train_error_x = []
- train_error_y = []
- test_error_x = []
- test_error_y = []
-
- # 学习过程
-
- n_batch = n_train // batch_size
-
- for i in range(epoch):
- # 统计误差
- forward_propagation(input_train)
- error_train = get_error(correct_train, n_train)
-
- forward_propagation(input_test)
- error_test = get_error(corre_test, n_test)
-
- train_error_x.append(i)
- train_error_y.append(error_train)
-
- test_error_x.append(i)
- test_error_y.append(error_test)
-
- index_random = np.arange(n_train)
-
- np.random.shuffle(index_random)
-
- for j in range(n_batch):
- mb_index = index_random[j * batch_size:(j + 1) * batch_size]
- x = input_train[mb_index, :]
- t = correct_train[mb_index, :]
-
- forward_propagation(x)
-
- back_propagation(t)
-
- update_wb()
-
- plt.plot(train_error_x, train_error_y, label="Train")
-
- plt.plot(test_error_x, test_error_y, label="Test")
-
- plt.legend()
-
- plt.xlabel("epoch")
-
- plt.ylabel("error")
-
- plt.show()

不同梯度下降方法更新参数下的分类结果与epoch的关系如图22所示:
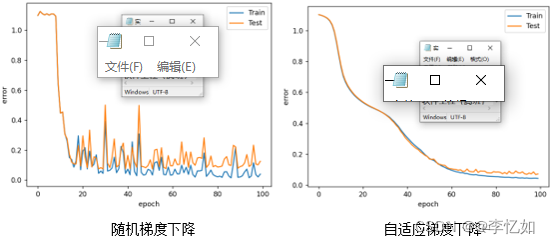
图22 不同梯度下降方法更新参数下的分类结果与epoch的关系
分析:由图22可见,无论哪种梯度下降更新参数,随着epoch增加,训练集与测试集的误差均会减小并呈现较相似趋势。但对于随机梯度下降而言,波动与误差较大。而自适应梯度下降更新BP神经网络的参数较为稳定,且两数据集拟合效果好(分类效果好,误差小)。
七、实验小结
1.最小二乘问题求解总结
(1)对于本实验,重点介绍的最小二乘问题求解方法有两种,分别是最小二乘法与梯度下降法,两种方法对比简单总结如表11所示:
表11 最小二乘问题求解的方法对比总结
| 方法 | 原理 | 优点 | 缺陷 |
| 最小二乘法 | 令∇fx=0,基于正规方程求解 | 得到的解相对精确 | 1.对异常点比较敏感 2.求逆的复杂度高 3.对于非线性数据效果不佳 |
| 梯度下降法 | 迭代,逐渐逼近精确解 | 效率相对较高 | 1.得到的解为局部最优,可能会停滞在局部最优 2.接近极小值点的情况下,存在锯齿现象,收敛速度降低 |
(2)通过实验中对给定优化模型使用不同方法进行求解,本实验中效率由高到低是梯度下降法>最小二乘法,解的精确度由高到低是最小二乘法>梯度下降法。针对表11中总计,在实际问题的求解方法的选择上,要根据数据的类型与任务的需求决定。
(3)从优化的角度来说,最小二乘法与梯度下降法均存在一定问题,在数学推导上仍有优化的空间,故对于最小二乘问题出现了许多其他优化方法求解,同样值得学习。
(4)不同语言与平台对于最小二乘问题求解的效率有一定影响,一般来说,随着矩阵与向量的规模增大,matlab下同方法的效率会高于Python,在选择的过程中要结合数据与个人熟悉度。
(5)最小二乘法与梯度下降法有多种应用,例如线性回归拟合数据与神经网络参数更新等,在理论与实践方面都有许多联系。
2.参考资料
1.最优化方法——Least Squares_显然易证的博客-CSDN博客_least_squares优化
3.梯度下降法求解BP神经网络的简单Demo_老饼讲解-BP神经网络的博客-


