- 1[python]数据同步工具DataX之Mysql同步数据至Hive (上)_datax 文件数据同步hive
- 2win11的ubuntu子系统 WSL2 下配置cuda、cudnn、GPU pytorch环境_wsl2安装cudnn
- 3一文看懂yolov7;yolov7详解
- 4[人工智能-sora] Sora的到来,到底意味着什么? 访谈摘要
- 5nRF52笔记(26)QSPI接口液晶显示屏_qspi发送数据到lcd,屏无显示
- 6CSS之margin塌陷问题_css margin塌陷
- 7《2020年度中国数据竞赛年鉴》发布!
- 8查看PostgrepSql的表结构/建表语句_postragesql 查看建表语句
- 9YoloV7目标检测(Pytorch版)【这也许是你见到最详细的博文!!!】
- 10Pycharm使用技巧_pytharm的操作技巧
Google的S2算法原理以及使用Java版本--部分参考自《高效的多维空间点索引算法》_google s2
赞
踩
相关资料
-
halfrost 的 git 仓库,包含空间搜索系列文章:https://github.com/halfrost/Halfrost-Field
-
s2 官网:https://s2geometry.io
-
s2 地图/可视化工具(功能强大,强烈推荐): http://s2.sidewalklabs.com/regioncoverer/
-
经纬度画圆/画矩形 地图/可视化工具 :https://www.mapdevelopers.com/draw-circle-tool.php
-
经纬度画多边形 地图/可视化工具 :http://apps.headwallphotonics.com
-
csdn参考文章:Google S2 常用操作 :https://blog.csdn.net/deng0515001/article/details/88031153
-
S2官方PPT:https://docs.google.com/presentation/d/1Hl4KapfAENAOf4gv-pSngKwvS_jwNVHRPZTTDzXXn6Q/view#slide=id.i0
-
S2jar:使用Maven工具
<!--google的S2包--> <dependency> <groupId>io.sgr</groupId> <artifactId>s2-geometry-library-java</artifactId> <version>1.0.0</version> </dependency> <!--附带的google common组件包--> <dependency> <groupId>com.google.guava</groupId> <artifactId>guava</artifactId> <version>21.0</version> </dependency>- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
直接下载源码,自己打jar,地址:https://github.com/google/s2-geometry-library-java
1.S2算法是什么?
S2其实是来自几何数学中的一个数学符号 S²,它表示的是单位球。S2 这个库其实是被设计用来解决球面上各种几何问题的。
2.为什么要使用S2算法?
S2 来解决多维空间点索引的问题的
-
s2有30级,geohash只有12级。s2的层级变化较平缓,方便选择。
-
s2功能强大,解决了向量计算,面积计算,多边形覆盖,距离计算等问题,减少了开发工作量。
-
s2解决了多边形覆盖问题。
这是其与geohash功能上最本质的不同。给定不规则范围,s2可以计算出一个多边形近似覆盖这个范围。其覆盖用的格子数量根据精确度可控。geohash在这方面十分不友好,划定一个大一点的区域,其格子数可能达到数千,若减少格子数则丢失精度,查询区域过大。
如下,在min level和max level不变的情况下,只需设置可接受的max cells数值,即可控制覆盖精度。而且其cell的region大小自动适配。geohash要在如此大范围实现高精度覆盖则会产生极为庞大的网格数。
另外需要注意的是,在minLevel,maxLevel,maxCells这3个参数中,不一定能完全满足.一般而言是优先满足maxLevel即最精细的网格大小,再尽可能控制cell数量在maxCells里面.而minLevel由于会合并网格,所以很难满足(在查询大区域的时候可能会出现一个大网格和很多个小网格,导致木桶效应.这个时候可能将大网格划分为指定等级的小网格,即最终效果为,严格遵循minLevel和maxLevel,为此牺牲maxCells)
eg:9个格子,maxcells为:10
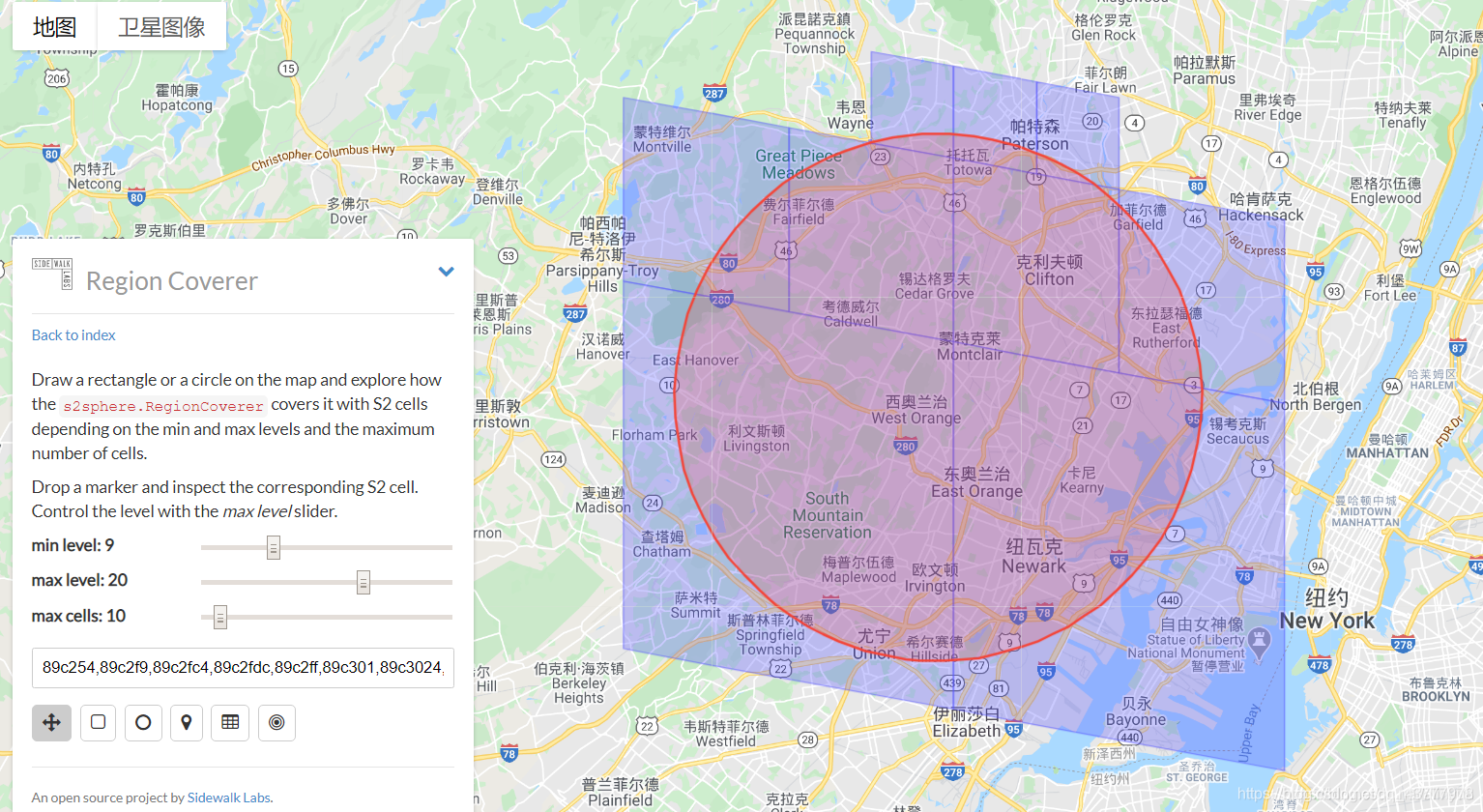
eg:34个格子,maxcells为:45
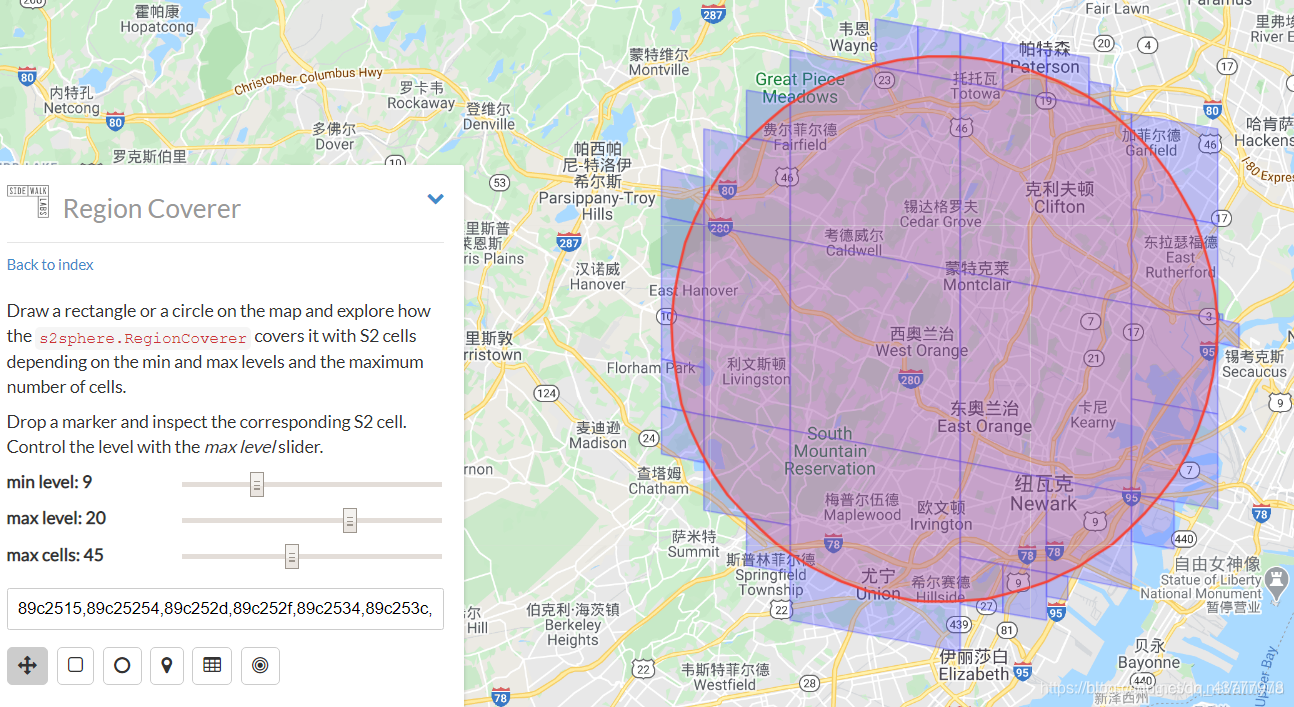
3.S2的原理是什么?
1)球面坐标变换
//经纬度转弧度计算球面坐标
S2LatLng ll = S2LatLng.fromDegrees(36.683, 117.1412);
//弧度转角度乘以 π / 180°
//角度转弧度乘以 180°/π
S2Point point = ll.toPoint();
- 1
- 2
- 3
- 4
- 5
- 6
- 7
球面上的一个点,在直角坐标系中,可以这样表示:
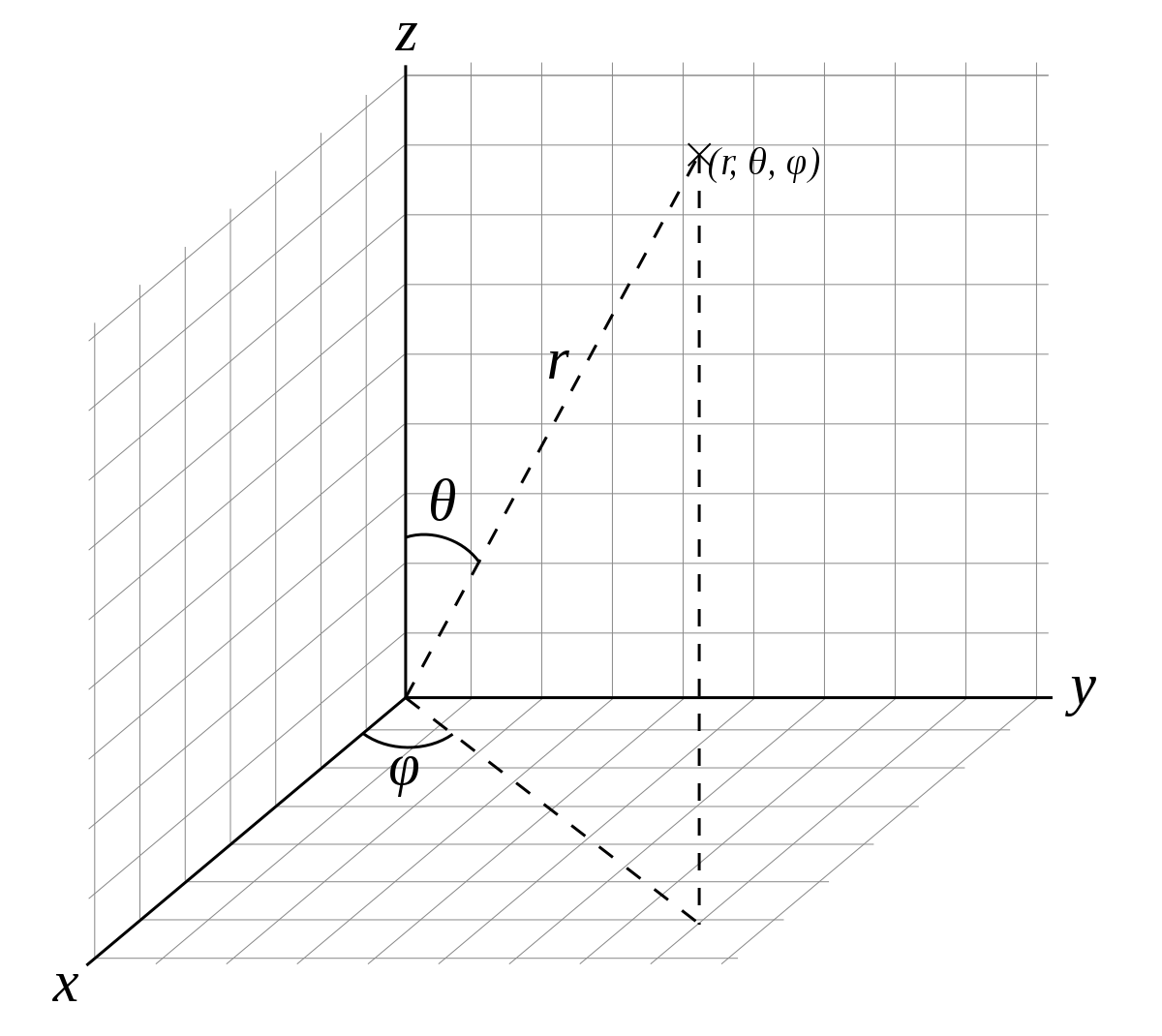
x = r * sin θ * cos φ
y = r * sin θ * sin φ
z = r * cos θ
- 1
- 2
- 3

再进一步,我们可以和球面上的经纬度联系起来。不过这里需要注意的是,纬度的角度 α 和直角坐标系下的球面坐标 θ 加起来等于 90°。所以三角函数要注意转换。
于是地球上任意的一个经纬度的点,就可以转换成 f(x,y,z)。
在 S2 中,地球半径被当成单位 1 了。所以半径不用考虑。x,y,z的值域都被限定在了[-1,1] x [-1,1] x [-1,1]这个区间之内了。
2)球面坐标转平面坐标(降维)
//投影
int face = S2Projections.xyzToFace(point);
R2Vector vector = S2Projections.validFaceXyzToUv(face, point);
- 1
- 2
- 3
首先在地球外面套了一个外切的正方体,如下图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FiBcpuxp-1620986757996)(C:\Users\余祥超\Desktop\notes\googleS2Img\球面外切正方形.png)]
从球心向外切正方体6个面分别投影。S2 是把球面上所有的点都投影到外切正方体的6个面上。

这里简单的画了一个投影图,上图左边的是投影到正方体一个面的示意图,实际上影响到的球面是右边那张图。
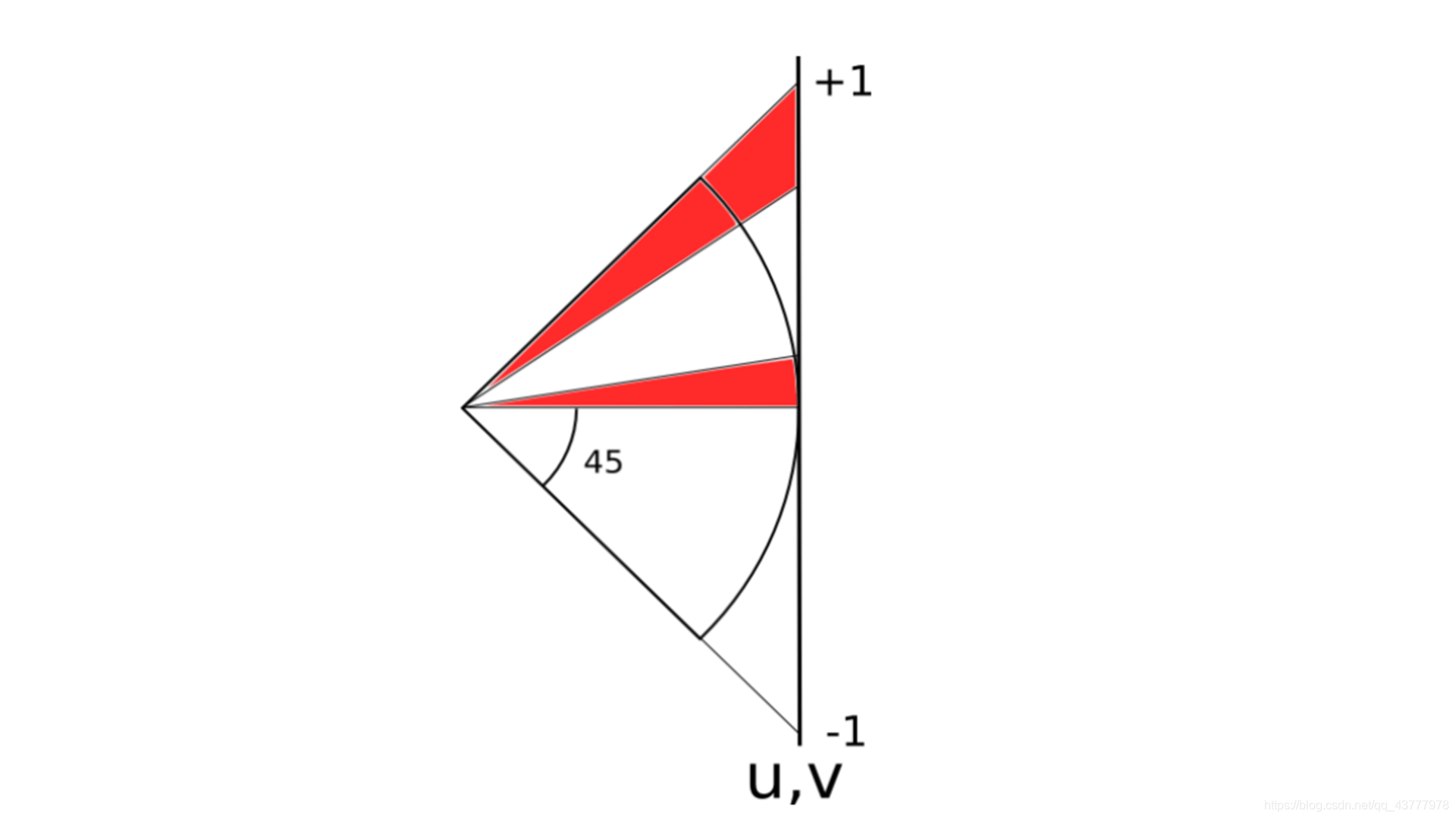
从侧面看,其中一个球面投影到正方体其中一个面上,边缘与圆心的连线相互之间的夹角为90°,但是和x,y,z轴的角度是45°。我们可以在球的6个方向上,把45°的辅助圆画出来,见下图左边。
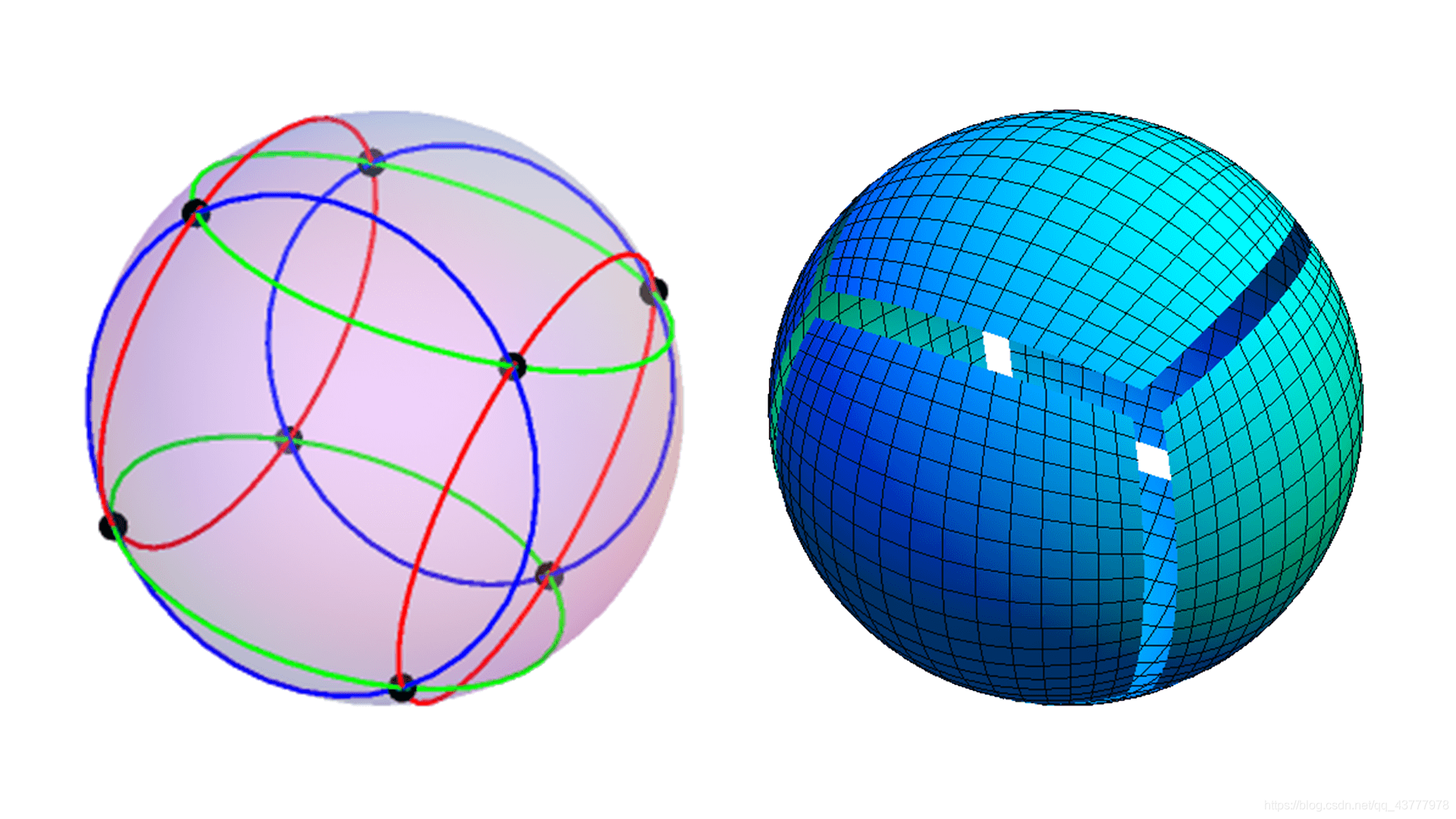
上图左边的图画了6个辅助线,蓝线是前后一对,红线是左右一对,绿线是上下一对。分别都是45°的地方和圆心连线与球面相交的点的轨迹。这样我们就可以把投影到外切正方体6个面上的球面画出来,见上图右边。
投影到正方体以后,我们就可以把这个正方体展开了。
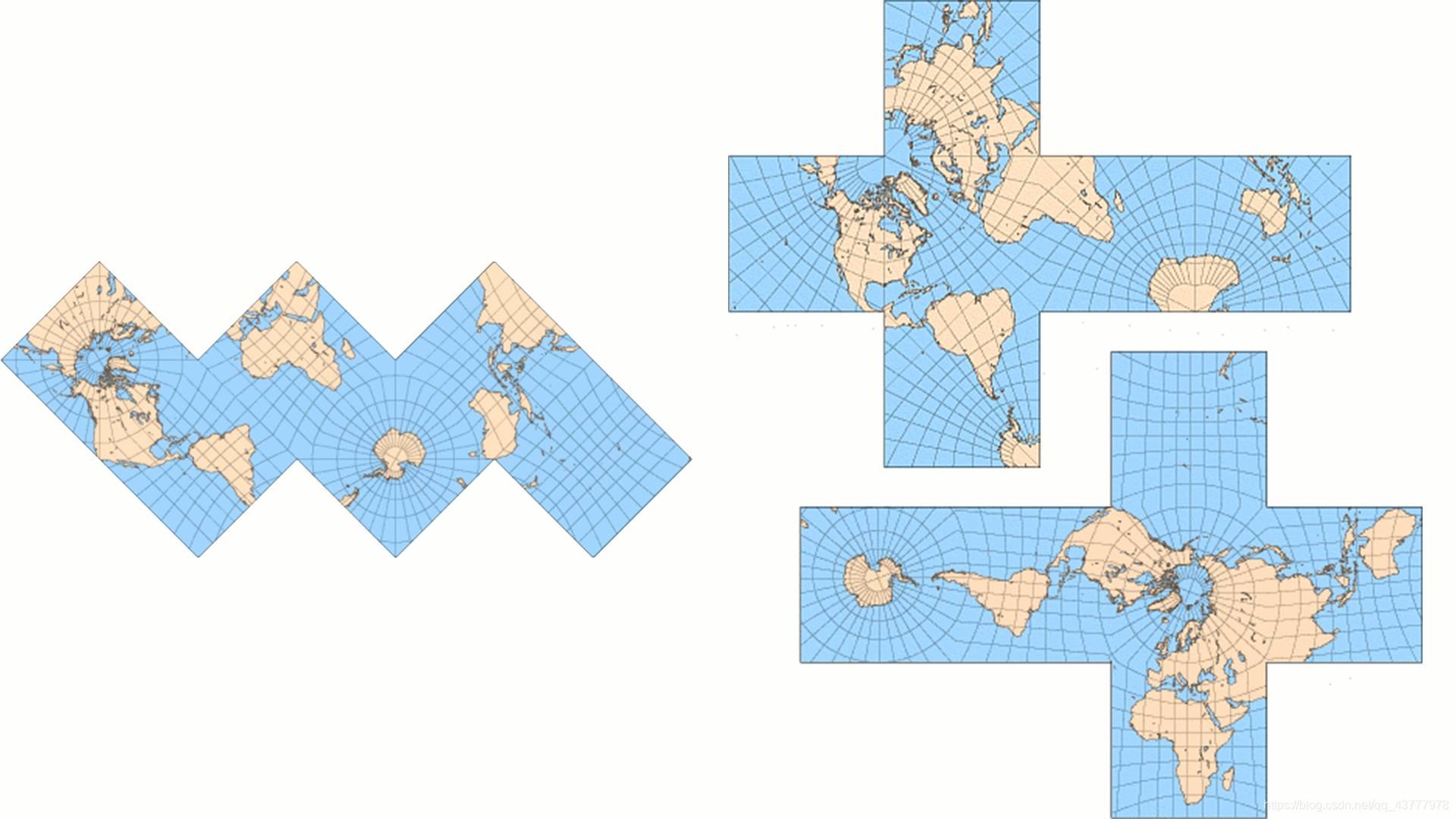
在 Google S2 中,它是把地球展开成如下的样子:

这样第一步的球面坐标进一步的被转换成 f(x,y,z) -> g(face,u,v),face是正方形的六个面,u,v对应的是六个面中的一个面上的x,y坐标。
remark:
1.默认定义 x 轴为0,y轴为1,z轴为2 。
2.最后 face 的值就是三个轴里面最长的轴,注意这里限定了他们三者都在 [0,5] 之间,所以如果是负轴就需要 + 3 进行修正。
3.主轴为 x 正半轴,face = 0;主轴为 y 正半轴,face = 1;主轴为 z 正半轴,face = 2;主轴为 x 负半轴,face = 3;主轴为 y 负半轴,face = 4;主轴为 z 负半轴,face = 5 。
4.如果直观的对应一个外切立方体的哪6个面,那就是 face = 0 对应的是前面,face = 1 对应的是右面,face = 2 对应的是上面,face = 3 对应的是后面,face = 4 对应的是左面,face = 5 对应的是下面。
3)球面矩形投影修正
//face是不变的,修正
double s = S2Projections.uvToST(vector.x());
double t = S2Projections.uvToST(vector.y());
- 1
- 2
- 3
上一步我们把球面上的球面矩形投影到正方形的某个面上,形成的形状类似于矩形,但是由于球面上角度的不同,最终会导致即使是投影到同一个面上,每个矩形的面积也不大相同。
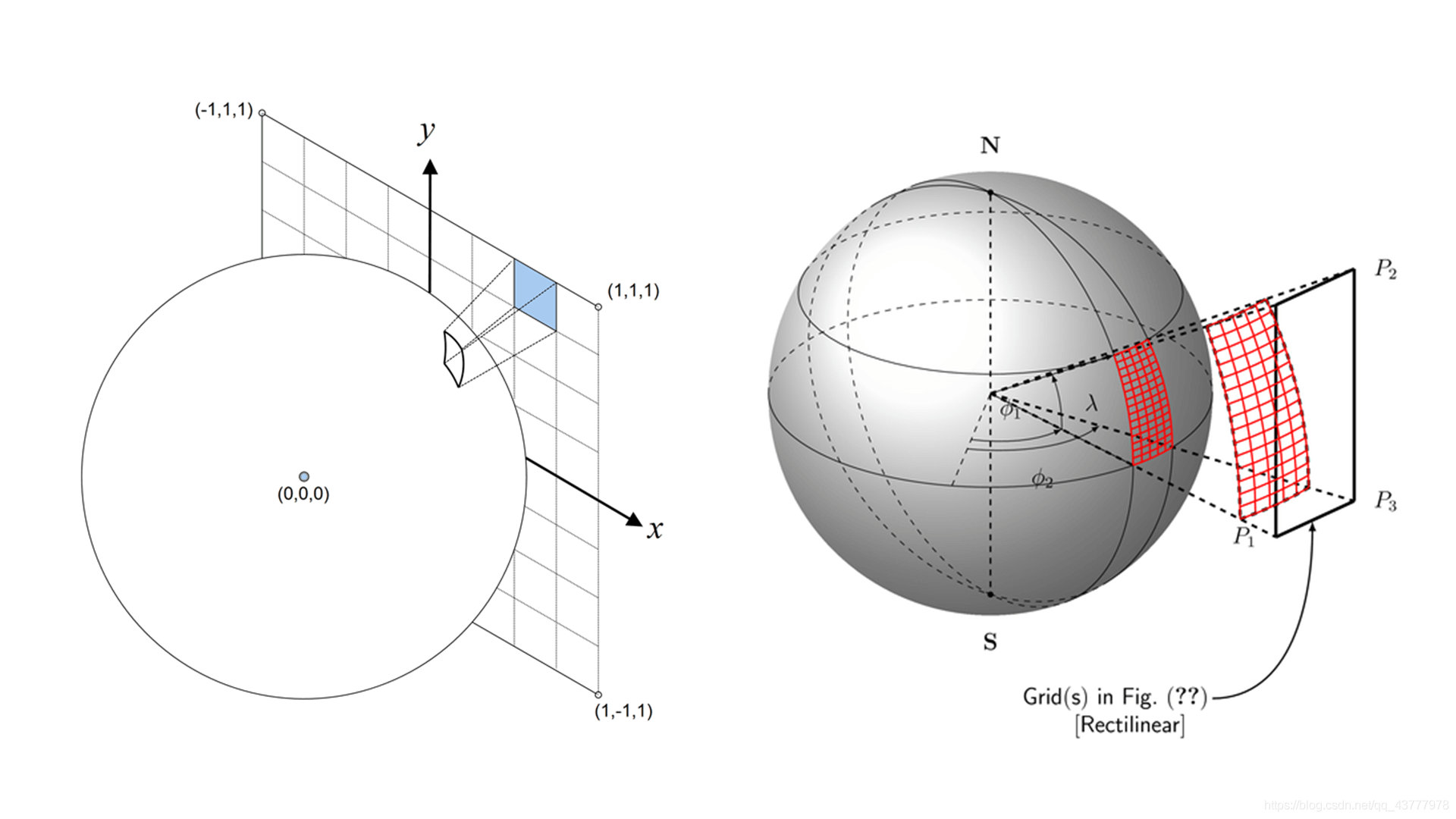
上图就表示出了球面上个一个球面矩形投影到正方形一个面上的情况。
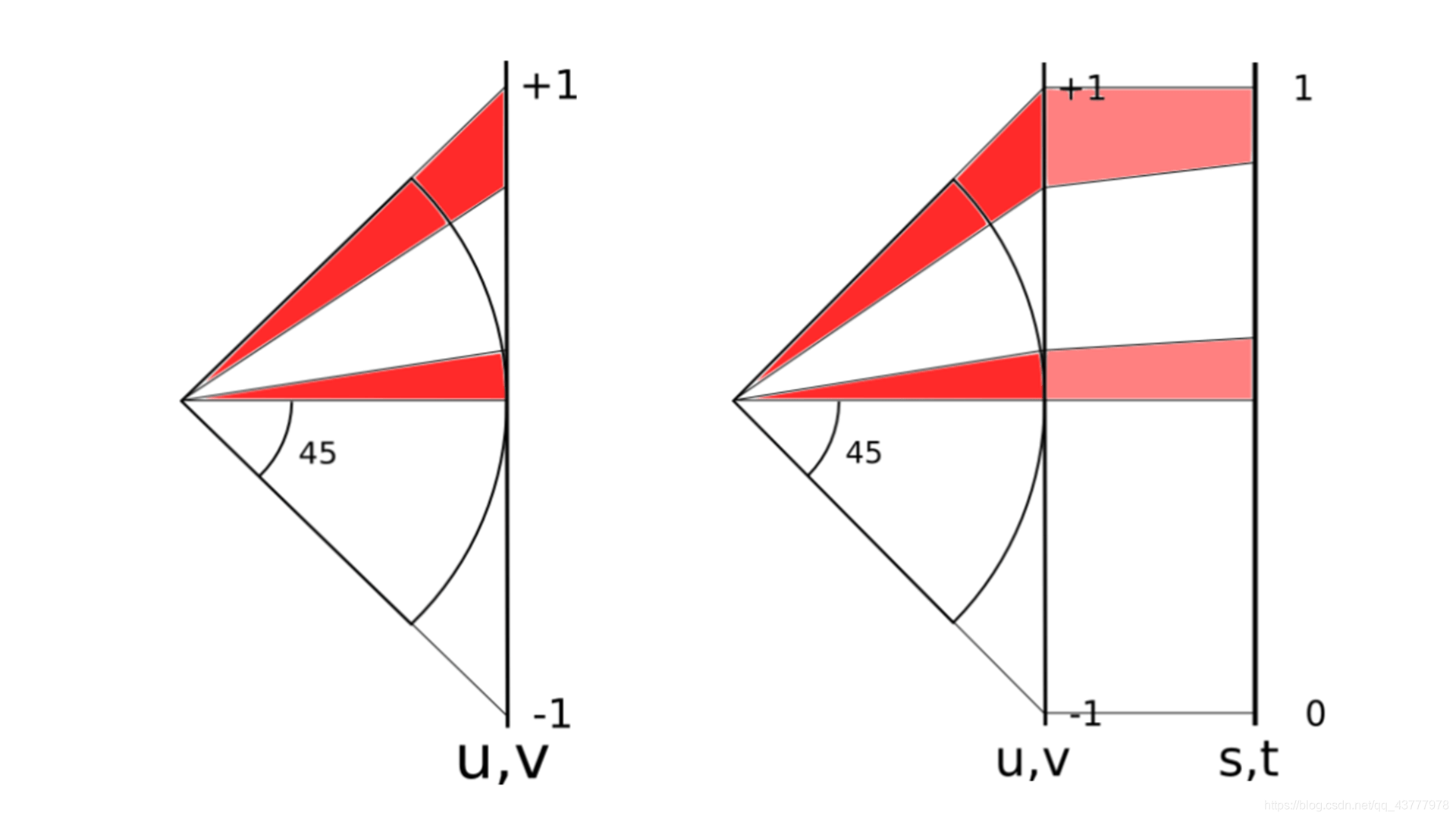
经过实际计算发现,最大的面积和最小的面积相差5.2倍。见上图左边。相同的弧度区间,在不同的纬度上投影到正方形上的面积不同。
现在就需要修正各个投影出来形状的面积。如何选取合适的映射修正函数就成了关键。目标是能达到上图右边的样子,让各个矩形的面积尽量相同。

线性变换是最快的变换,但是变换比最小。tan() 变换可以使每个投影以后的矩形的面积更加一致,最大和最小的矩形比例仅仅只差0.414。可以说非常接近了。但是 tan() 函数的调用时间非常长。如果把所有点都按照这种方式计算的话,性能将会降低3倍。
最后谷歌选择的是二次变换,这是一个近似切线的投影曲线。它的计算速度远远快于 tan() ,大概是 tan() 计算的3倍速度。生成的投影以后的矩形大小也类似。不过最大的矩形和最小的矩形相比依旧有2.082的比率。
上表中,ToPoint 和 FromPoint 分别是把单位向量转换到 Cell ID 所需要的毫秒数、把 Cell ID 转换回单位向量所需的毫秒数(Cell ID 就是投影到正方体六个面,某个面上矩形的 ID,矩形称为 Cell,它对应的 ID 称为 Cell ID)。ToPointRaw 是某种目的下,把 Cell ID 转换为非单位向量所需的毫秒数。
S2的矩形面积修正源码
//S2_LINEAR_PROJECTION 线性变换,未实现 //sttoUV return 2 * s - 1 //uvToST return 0.5 * (u + 1); //S2_TAN_PROJECTION tan()变换 //S2_QUADRATIC_PROJECTION 二次变换 public static strictfp double stToUV(double s) { switch(S2_PROJECTION) { case S2_LINEAR_PROJECTION: return s; case S2_TAN_PROJECTION: s = Math.tan(0.7853981633974483D * s); return s + 1.1102230246251565E-16D * s; case S2_QUADRATIC_PROJECTION: if (s >= 0.0D) { return 0.3333333333333333D * ((1.0D + s) * (1.0D + s) - 1.0D); } return 0.3333333333333333D * (1.0D - (1.0D - s) * (1.0D - s)); default: throw new IllegalStateException("Invalid value for S2_PROJECTION"); } } public static strictfp double uvToST(double u) { switch(S2_PROJECTION) { case S2_LINEAR_PROJECTION: return u; case S2_TAN_PROJECTION: return 1.2732395447351628D * Math.atan(u); case S2_QUADRATIC_PROJECTION: if (u >= 0.0D) { return Math.sqrt(1.0D + 3.0D * u) - 1.0D; } return 1.0D - Math.sqrt(1.0D - 3.0D * u); default: throw new IllegalStateException("Invalid value for S2_PROJECTION"); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
经过修正变换以后,u,v都变换成了s,t。值域也发生了变化。u,v的值域是[-1,1],变换以后,使s,t的值域是[0,1]。
至此,小结一下,球面上的点S(lat,lng) -> f(x,y,z) -> g(face,u,v) -> h(face,s,t)。目前总共转换了4步,球面经纬度坐标转换成球面xyz坐标,再转换成外切正方体投影面上的坐标,最后变换成修正后的坐标。
4)点与坐标轴点相互转换
int i = S2CellId.stToIJ(s);
int j = S2CellId.stToIJ(t);
- 1
- 2
在 S2 算法中,默认划分 Cell 的等级是30,也就是说把一个正方形划分为 2^30 * 2^30个小的正方形。
那么上一步的s,t映射到这个正方形上面来,对应该如何转换呢?

s,t的值域是[0,1],现在值域要扩大到[0,230-1]。
S2源码
private static strictfp int stToIJ(double s) {
int m = 536870912;
return (int)Math.max(0L, Math.min(1073741823L, Math.round(5.36870912E8D * s + 5.368709115E8D)));
}
- 1
- 2
- 3
- 4
到这一步,是h(face,s,t) -> H(face,i,j)。
5)坐标轴点与CellId相互转换
S2CellId cellid = S2CellId.fromFaceIJ(face, i, j);
S2LatLng lan = cellid.toLatLng();
- 1
- 2
- 3
- 4

1.生成希尔伯特曲线
static int lookupBits = 4; static int swapMask = 0x01; static int invertMask = 0x02; //在整个库中,没有使用 static int ijToPos[][] ={ {0, 1, 3, 2}, // 标准顺序 {0, 3, 1, 2}, // 轴旋转 {2, 3, 1, 0}, // 上下倒置 {2, 1, 3, 0}, // 轴旋转左右倒置 }; //数组存的值是ij组合的二进制的数值,表示方向 static int posToIJ[][] = { {0, 1, 3, 2}, // 标准顺序: (0,0), (0,1), (1,1), (1,0) {0, 2, 3, 1}, // 轴旋转: (0,0), (1,0), (1,1), (0,1) {3, 2, 0, 1}, // 上下倒置: (1,1), (1,0), (0,0), (0,1) {3, 1, 0, 2}, // 轴旋转左右倒置: (1,1), (0,1), (0,0), (1,0) }; //posToOrientation 数组里面装了4个数字,分别是1,0,0,3,表示子格子的方向 static int posToOrientation[] = {swapMask, 0, 0, invertMask | swapMask};//1 | 2=3 //希尔伯特曲线 ID 转换成坐标轴 IJ 的转换表 static int[] lookupIJ = new int[1 << (2 * lookupBits + 2)];//1<<10=2^10=1024 //坐标轴 IJ 转换成希尔伯特曲线 ID 的转换表 static int[] lookupPos = new int[1 << (2 * lookupBits + 2)];
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
1.解释变量。
posToIJ 代表的是一个矩阵,里面记录了一些单元希尔伯特曲线的位置信息。
注意在下面一阶曲线中:横着的是i,竖着的是j
把 posToIJ 数组里面的信息用图表示出来,如下图:
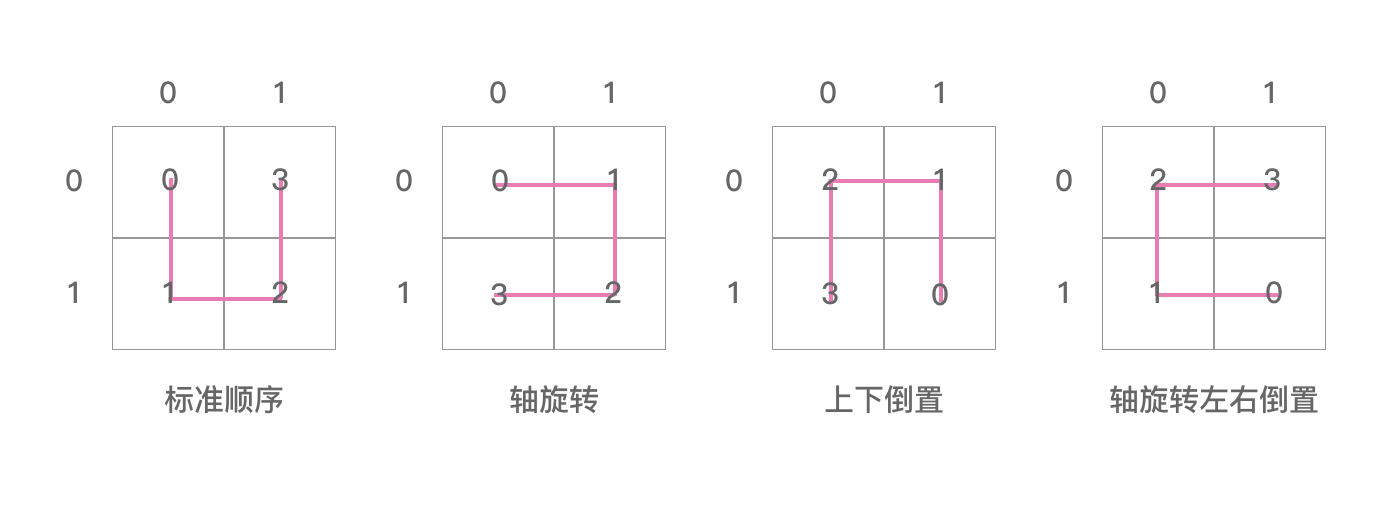
从上面这四张图我们可以看出:
posToIJ 的四张图其实是“ U ” 字形逆时针分别旋转90°得到的。这里我们只能看出四张图相互之间的联系,即兄弟之间的联系,但是看不到父子图相互之间的联系。
同理,把 ijToPos 数组里面的信息用图表示出来,如下图:
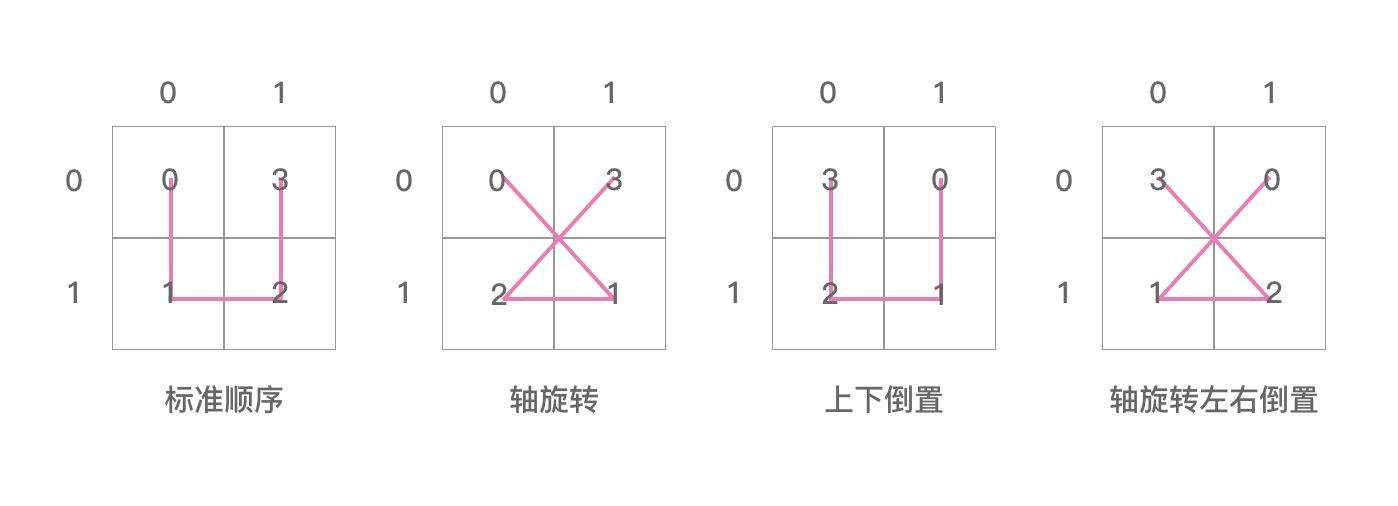
这里是初始化的递归函数,在希尔伯特曲线的标准顺序中可以看到是有4个格子,并且格子都有顺序的,所以初始化要遍历满所有顺序。入参的第4个参数origOrientation,就是从0 - 3 。
public static void init() {
initLookupCell(0, 0, 0, 0, 0, 0);
initLookupCell(0, 0, 0, swapMask, 0, swapMask);
initLookupCell(0, 0, 0, invertMask, 0, invertMask);
initLookupCell(0, 0, 0, swapMask | invertMask, 0, swapMask | invertMask);
}
- 1
- 2
- 3
- 4
- 5
- 6
下面这个函数是生成希尔伯特曲线的。我们可以看到有一处对 pos << 2的操作,这里是把位置变换到第一个4个小格子中,所以位置乘以了4。
public static void initLookupCell(int level, int i, int j, int origOrientation, int pos, int orientation) { if (level == lookupBits) { int ij = (i << lookupBits) + j; lookupPos[(ij << 2) + origOrientation] = (pos << 2) + orientation; lookupIJ[(pos << 2) + origOrientation] = (ij << 2) + orientation; return; } level++; i <<= 1; j <<= 1; pos <<= 2; int r[] = posToIJ[orientation]; initLookupCell(level, i + (r[0] >> 1), j + (r[0] & 1), origOrientation, pos, orientation ^ posToOrientation[0]); initLookupCell(level, i + (r[1] >> 1), j + (r[1] & 1), origOrientation, pos + 1, orientation ^ posToOrientation[1]); initLookupCell(level, i + (r[2] >> 1), j + (r[2] & 1), origOrientation, pos + 2, orientation ^ posToOrientation[2]); initLookupCell(level, i + (r[3] >> 1), j + (r[3] & 1), origOrientation, pos + 3, orientation ^ posToOrientation[3]); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
2.r[0] >> 1和r[0] & 1
r 数组来自于 posToIJ 数组。posToIJ 数组上面说过了,它里面装的其实是4个不同方向的“ U ”字。相当于表示了当前四个小方格兄弟相互之间的方向。r[0]、r[1]、r[2]、r[3] 取出的其实就是 00,01,10,11 这4个数。
那么 r[0]>>1 操作就是取出二位二进制位的前一位,即 i 位。r[0]&1 操作就是取出二位二进制位的后一位,即 j 位。r[1]、r[2]、r[3] 同理。
3.orientation^posToOrientation[0]
posToOrientation[] = {swapMask, 0, 0, invertMask | swapMask};
//数值代入:
posToOrientation = [4]int{1, 0, 0, 3}
//根据上一次的原始的方向推算出当前的 pos 所在的方向。即计算父子之间关系。
orientation^posToOrientation[0]
//举个例子,假设 orientation = 0,即图0,那么:
00 ^ 01 = 01
00 ^ 00 = 00
00 ^ 00 = 00
00 ^ 11 = 11
//图0 的四个孩子的方向就被我们算出来了,01,00,00,11,1003 。和上面图片中图0展示的是一致的。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
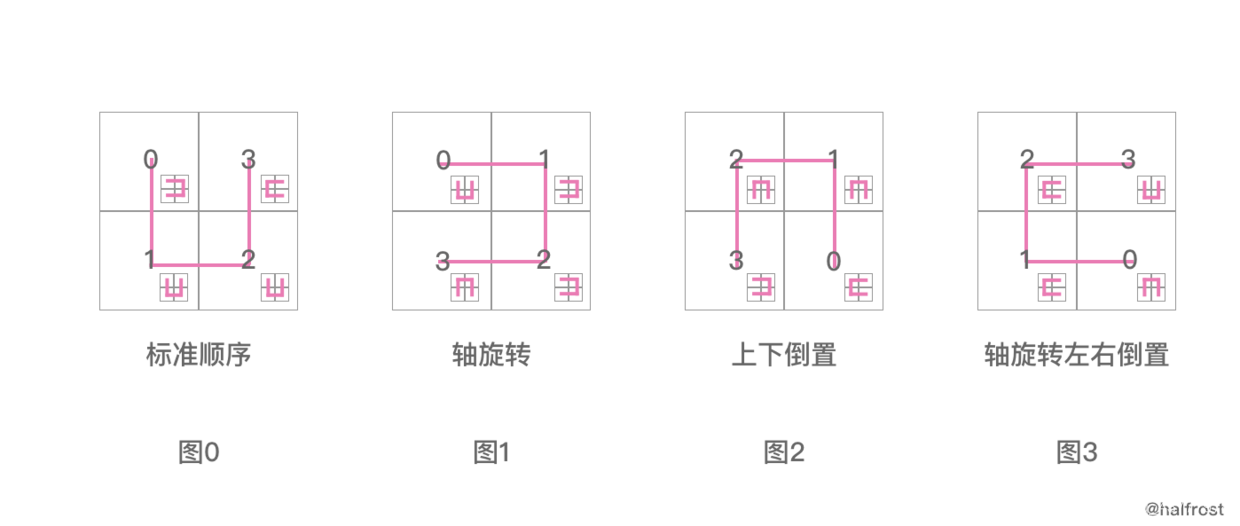
其实这个对应的就是 图0 中4个小方块接下来再划分的方向。
图0 中0号的位置下一个图的方向应该是图1,即01;
图0 中1号的位置下一个图的方向应该是图0,即00;
图0 中2号的位置下一个图的方向应该是图0,即00;
图0 中3号的位置下一个图的方向应该是图3,即11 。
这就是初始化 posToOrientation 数组里面的玄机了。
posToIJ 的四张图我们只能看出兄弟之间的关系,那么 posToOrientation 的四张图让我们知道了父子之间的关系。
eg:
//orientation = 1,orientation = 2,orientation = 3,都是同理的: 01 ^ 01 = 00 01 ^ 00 = 01 01 ^ 00 = 01 01 ^ 11 = 10 10 ^ 01 = 11 10 ^ 00 = 10 10 ^ 00 = 10 10 ^ 11 = 01 11 ^ 01 = 10 11 ^ 00 = 11 11 ^ 00 = 11 11 ^ 11 = 00 //图1孩子的方向是0,1,1,2 。图2孩子的方向是3,2,2,1 。图3孩子的方向是2,3,3,0 。和图上画的是完全一致的。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
注意:
i,j 并不是直接对应的 希尔伯特曲线 坐标系上的坐标。因为初始化需要生成的是五阶希尔伯特曲线
pos 参数对应的就是希尔伯特曲线坐标系上的坐标。一旦一个希尔伯特曲线的起始点和阶数确定以后,四个小方块组成的一个大方块的 pos 位置确定以后,那么它的坐标其实就已经确定了。希尔伯特曲线上的坐标并不依赖 i,j,完全是由曲线的性质和 pos 位置决定的。
2.pos 和 i,j 的转换关系
初始化计算 lookupPos 数组和 lookupIJ 数组有什么用呢?这两个数组就是把 i,j 和 pos 联系起来的数组。知道 pos 以后可以立即找到对应的 i,j。知道 i,j 以后可以立即找到对应的 pos。
将 i,j 分别4位4位的取出来,i 的4位二进制位放前面,j 的4位二进制位放后面。最后再加上希尔伯特曲线的方向位 orientation 的2位。组成 iiii jjjj oo 类似这样的10位二进制位。通过 lookupPos 数组这个桥梁,找到对应的 pos 的值。pos 的值就是对应希尔伯特曲线上的位置。然后依次类推,再取出 i 的4位,j 的4位进行这样的转换,直到所有的 i 和 j 的二进制都取完了,最后把这些生成的 pos 值安全先生成的放在高位,后生成的放在低位的方式拼接成最终的 CellID。
在 Google S2 中,i,j 每次转换都是4位,所以 i,j 的有效值取值是 0 - 15,所以 iiii jjjj oo 是一个十位的二进制的数,能表示的范围是 2^10 = 1024 。那么 pos 初始化值也需要计算到 1024 。由于 pos 是4个小方块组成的大方块,它本身就是一个一阶的希尔伯特曲线。所以初始化需要生成一个五阶的希尔伯特曲线。

remark:
为何要 iiii jjjj oo 这样设计,为何是4位4位的,谷歌开发者在注释里面这样写道:“我们曾经考虑过一次组合 16 位,14位的 position + 2位的 orientation,但是代码实际运行起来发现小数组拥有更好的性能,2KB 更加适合存储到主 cache 中。
3.S2 Cell ID 数据结构
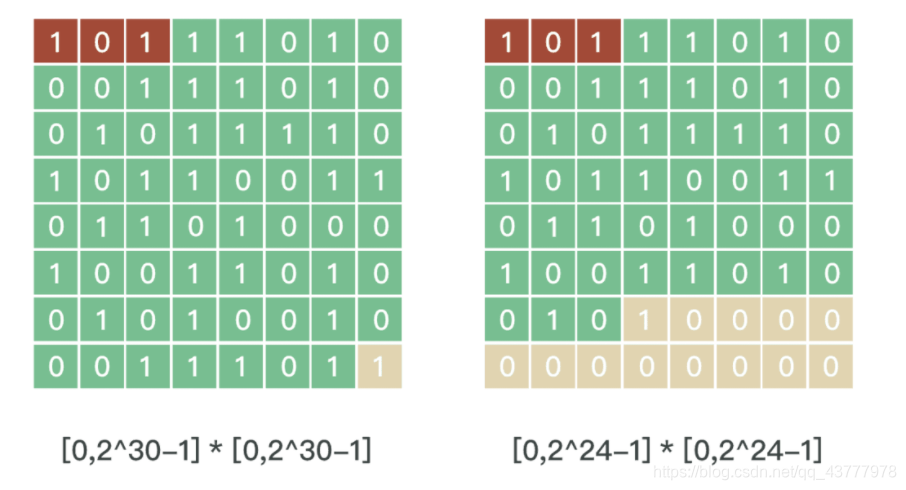
上图左图中对应的是 Level 30 的情况,右图对应的是 Level 24 的情况。(2的多少次方,角标对应的也就是 Level 的值)
在 S2 中,每个 CellID 是由64位的组成的。可以用一个 uint64 存储。开头的3位表示正方体6个面中的一个,取值范围[0,5]。3位可以表示0-7,但是6,7是无效值。
64位的最后一位是1,这一位是特意留出来的。用来快速查找中间有多少位。从末尾最后一位向前查找,找到第一个不为0的位置,即找到第一个1。这一位的前一位到开头的第4位(因为前3位被占用)都是可用数字。
绿色格子有多少个就能表示划分多少格。上图左图,绿色的有60个格子,于是可以表示[0,230 -1] * [0,230 -1]这么多个格子。上图右图中,绿色格子只有48个,那么就只能表示[0,224 -1]*[0,224 -1]这么多个格子。
6)源码
public static strictfp S2CellId fromLatLng(S2LatLng ll) { return fromPoint(ll.toPoint()); } public static strictfp S2CellId fromPoint(S2Point p) { int face = S2Projections.xyzToFace(p); R2Vector uv = S2Projections.validFaceXyzToUv(face, p); int i = stToIJ(S2Projections.uvToST(uv.x())); int j = stToIJ(S2Projections.uvToST(uv.y())); return fromFaceIJ(face, i, j); } public static strictfp S2CellId fromFaceIJ(int face, int i, int j) { long[] n = new long[]{0L, (long)(face << 28)}; int bits = face & 1; for(int k = 7; k >= 0; --k) { bits = getBits(n, i, j, k, bits); } S2CellId s = new S2CellId(((n[1] << 32) + n[0] << 1) + 1L); return s; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
具体步骤如下:
-
将 face 左移 60 位。
-
计算初始的 origOrientation。初始的 origOrientation 是 face 转换得来的,face & 01 以后的结果是为了使每个面都有一个右手坐标系。
-
循环,从头开始依次取出 i ,j 的4位二进制位,计算出 ij<<2 + origOrientation,然后查 lookupPos 数组找到对应的 pos<<2 + orientation 。
-
拼接 CellID,右移 pos<<2 + orientation 2位,只留下 pos ,把pos 继续拼接到 上次循环的 CellID 后面。
-
计算下一个循环的 origOrientation。&= (swapMask | invertMask) 即 & 11,也就是取出末尾的2位二进制位。
-
最后拼接上最后一个标志位 1 .
注意:由于 CellID 是64位的,头三位是 face ,末尾一位是标志位,所以中间有 60 位。i,j 转换成二进制是30位的。7个4位二进制位和1个2位二进制位。4*7 + 2 = 30 。iijjoo ,即 i 的头2个二进制位和 j 的头2个二进制位加上 origOrientation,这样组成的是6位二进制位,最多能表示 26 = 32,转换出来的 pos + orientation 最多也是32位的。即转换出来最多也是6位的二进制位,除去末尾2位 orientation ,所以 pos 在这种情况下最多是 4位。iiiijjjjpppp,即 i 的4个二进制位和 j 的4个二进制位加上 origOrientation,这样组成的是10位二进制位,最多能表示 210 = 1024,转换出来的 pos + orientation 最多也是10位的。即转换出来最多也是10位的二进制位,除去末尾2位 orientation ,所以 pos 在这种情况下最多是 8位。
由于最后 CellID 只拼接 pos ,所以 4 + 7 * 8 = 60 位。拼接完成以后,中间的60位都由 pos 组成的。最后拼上头3位,末尾的1位标志位,64位的 CellID 就这样生成了。
7)举例
最后举个具体的完整的例子:
| 纬度 | 经度 | ||
|---|---|---|---|
| 直角坐标系 | -0.209923466239598816018841 | 0.834295703289209877873134 | 0.509787031803590306999752 |
| (face,u,v) | 1 | 0.25161758044776666 | 0.6110387837235114 |
| (face,s,t) | 1 | 0.6623542747924445 | 0.8415931842598497 |
| (face,i,j) | 1 | 711197487 | 903653800 |
用表展示出每一步(表比较长,请右滑):
| i | j | orientation | ij<<2 + origOrientation | pos<<2 + orientation | CellID | |
|---|---|---|---|---|---|---|
| 711197487 | 903653800 | 1 | ||||
| 对应二 进制 | 101010011001000000001100101111 | 110101110111001010100110101000 | 01 | |||
| 进行转换 | i 左移6位,给 j 的4位和方向位 orientation 2位留出位置 | j 左移2位,给方向位 orientation 留出位置 | orientation 初始值是 face 的值 | [iiii jjjj oo] i的四位,j的四位,o的两位依次排在一起组成10位二进制位 | 从前面一列转换过来是通过查 lookupPos 数组查出来的 | 初始值:face 左移 60 位,接着以后每次循环都拼接 pos ,注意不带orientation ,即前一列需要右移2位去掉末尾的 orientation |
| 取 i , j 的首两位 | 10 000000 | 11 00 | 01 | (00)10001101 | 101110 | 1101100000000000000000000000000000000000000000000000000000000 |
| 再取 i , j 的3,4,5,6位 | 1010 000000 | 0101 00 | 10 | 1010010110 | 111011110 | 1101101110111000000000000000000000000000000000000000000000000 |
| 再取 i , j 的7,8,9,10位 | 0110 000000 | 1101 00 | 10 | (0)110110110 | 1110011110 | 1101101110111111001110000000000000000000000000000000000000000 |
| 再取 i , j 的11,12,13,14位 | 0100 000000 | 1100 00 | 10 | (0)100110010 | 1110000001 | 1101101110111111001111110000000000000000000000000000000000000 |
| 再取 i , j 的15,16,17,18位 | 0000 000000 | 1010 00 | 01 | (0000)101001 | 1110110000 | 1101101110111111001111110000011101100000000000000000000000000 |
| 再取 i , j 的19,20,21,22位 | 0011 000000 | 1001 00 | 00 | (00)11100100 | 100011001 | 1101101110111111001111110000011101100010001100000000000000000 |
| 再取 i , j 的23,24,25,26位 | 0010 000000 | 1010 00 | 01 | (00)10101001 | 1110001011 | 1101101110111111001111110000011101100010001101110001000000000 |
| 再取 i , j 的27,28,29,30位 | 1111 000000 | 1000 00 | 11 | 1111100011 | 1010110 | 1101101110111111001111110000011101100010001101110001000010101 |
| 最终结果 | 11011011101111110011111100000111011000100011011100010000101011(拼接上末尾的标志位1) |
//eg后面一部转换过程推算 pos<<2 + orientation CellID 0000101110 1101100000000000000000000000000000000000000000000000000000000 0111011110 1101101110111000000000000000000000000000000000000000000000000 1110011110 1101101110111111001110000000000000000000000000000000000000000 //去掉方向位,首位+ face 00001011 1101100000000000000000000000000000000000000000000000000000000 01110111 1101101110111000000000000000000000000000000000000000000000000 11100111 1101101110111111001110000000000000000000000000000000000000000 //反推,cellid,去掉首位face, 1011 00000000000000000000000000000000000000000000000000000000 1011 01110111 000000000000000000000000000000000000000000000000 1011 01110111 11100111 0000000000000000000000000000000000000000 eg: origOrientation初始值:01 & 1 =01 face & 1 后续计算:01 ^ 01 00 00 11 与数组posToOrientation的值异或运算 01 10 10 10 01 00 ^ ^ ^ ^ ^ ^ 01 00 00 11 01 00 10 10 10 01 00 00
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
4.S2如何使用?
1)经纬度 转 CellId
//注意使用的是WGS84坐标(GPS导航坐标) //parent()可以指定等级,默认是30级 double lat = 36.683; double lng = 117.1412; int currentlevel = 4; S2LatLng s2LatLng = S2LatLng.fromDegrees(lat, lng); S2CellId cellId = S2CellId.fromLatLng(s2LatLng ).parent(currentlevel); //CellID(face=1, pos=15d0000000000000, level=4) System.out.println("CellID" + cellid); //CellID.pos:1571756269952303104 System.out.println("CellID.pos:" + cellid.pos()); //CellID.id: 3877599279165997056,level:4 System.out.println("CellID.id: " + cellid.id() + ",level:" + cellid.level());
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
2)CellId 转 经纬度
S2LatLng s2LatLng = new S2CellId(cellId.id()).toLatLng();
Double lat = s2LatLng.latDegrees();
Double lng = s2LatLng.lngDegrees();
- 1
- 2
- 3
//经纬度转S2LatLng
S2LatLng s2LatLng = S2LatLng.fromDegrees(lat, lng);
//S2LatLng转S2CellId
S2CellId cellId = S2CellId.fromLatLng(s2LatLng);
//S2CellId转token
String token=s2CellId.toToken(); //任意形状的所有S2块的token集合,可以借用工具在地图上显示
//token转S2CellId
S2CellId s2CellId = S2CellId.fromToken(token);
//S2LatLng转point
S2Point point = s2LatLng.toPoint();
//point转S2LatLng
S2LatLng latLng = new S2LatLng(point);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
3)S2计算距离
S2LatLng startS2 = S2LatLng.fromDegrees(55.8241, 137.8347);
S2LatLng endS2 = S2LatLng.fromDegrees(55.8271, 137.8347);
double distance = startS2.getEarthDistance(endS2);
System.out.println("距离为:"+distance+" m");
- 1
- 2
- 3
- 4
4)经纬度构建S2矩形
S2LatLng startS2 = S2LatLng.fromDegrees(0.8293, 72.004); //左下角
S2LatLng endS2 = S2LatLng.fromDegrees(55.8271, 137.8347); //右上角
S2LatLngRect rect = new S2LatLngRect(startS2, endS2);
- 1
- 2
- 3
5)经纬度构建S2多边形
//注意,一般需要多边形内侧,此处需要按照逆时针顺序添加。
//多边形经纬度可借用工具获取
List<S2Point> pointList = Lists.newArrayList();
pointList.add(S2LatLng.fromDegrees(lat, lng).toPoint());
pointList.add(S2LatLng.fromDegrees(lat, lng).toPoint());
pointList.add(S2LatLng.fromDegrees(lat, lng).toPoint());
pointList.add(S2LatLng.fromDegrees(lat, lng).toPoint());
S2Loop s2Loop = new S2Loop(pointList);
S2Polygon s2Polygon = new S2Polygon(s2Loop);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
6)经纬度构建圆形
double radius = 600.5; //半径
Double capHeight = (2 * S2.M_PI) * (radius / 40075017);//40075017为地球周长
S2LatLng s2LatLng= S2LatLng.fromDegrees(lat, lng);
S2Cap cap = S2Cap.fromAxisHeight(s2LatLng.toPoint(),capHeight * capHeight / 2);
- 1
- 2
- 3
- 4
7)获取任意形状内所有S2块
//S2Region cap 任意区域
S2RegionCoverer coverer = new S2RegionCoverer();
//最小格子和最大格子,总格子数量
coverer.setMaxLevel(15);
coverer.setMinLevel(7);
coverer.setMaxCells(200);
List<S2CellId> list = coverer.getCovering(cap).cellIds();
for (S2CellId s:list) {
System.out.println(s);
}
//可以用于区域内目标检索,根据cellid建立索引,查询区域内cellid in (list)的餐馆、出租车
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
8)判断点是否在任意形状内
//S2Region cap 任意区域
S2LatLng s2LatLng = S2LatLng.fromDegrees(lat, lng);
boolean contains = cap.contains(s2LatLng.toPoint());
System.out.println(contains);
- 1
- 2
- 3
- 4
9)不同等级S2块包含的S2子块
public static List<S2CellId> childrenCellId(S2CellId s2CellId, Integer desLevel) { return childrenCellId(s2CellId, s2CellId.level(), desLevel); } //递归调用,每个格子一分为四 private static List<S2CellId> childrenCellId(S2CellId s2CellId, Integer curLevel, Integer desLevel) { if (curLevel < desLevel) { //计算当前格子每个格子的差值 long interval = (s2CellId.childEnd().id() - s2CellId.childBegin().id()) / 4; List<S2CellId> s2CellIds = Lists.newArrayList(); for (int i = 0; i < 4; i++) { long id = s2CellId.childBegin().id() + interval * i; s2CellIds.addAll(childrenCellId(new S2CellId(id), curLevel + 1, desLevel)); } return s2CellIds; } else { return Lists.newArrayList(s2CellId); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
10)判断当前cellId的level
getLevel(cellId.id())
//判断当前cellId的level
private static int getLevel(long input) {
int n = 0;
while (input % 2 == 0) {
input = input / 2;
n++;
}
return 30 - n / 2;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
5.S2与GeoHash的区别是什么?
Geohash 有12级,从5000km 到 3.7cm。中间每一级的变化比较大。有时候可能选择上一级会大很多,选择下一级又会小一些。比如选择字符串长度为4,它对应的 cell 宽度是39.1km,需求可能是50km,那么选择字符串长度为5,对应的 cell 宽度就变成了156km,瞬间又大了3倍了。这种情况选择多长的 Geohash 字符串就比较难选。选择不好,每次判断可能就还需要取出周围的8个格子再次进行判断。Geohash 需要 12 bytes 存储(精度为12时)。
S2 有30级,从 0.7cm² 到 85,000,000km² 。中间每一级的变化都比较平缓,接近于4次方的曲线。所以选择精度不会出现 Geohash 选择困难的问题。S2 的存储只需要一个 8个bytes 即可存下。
S2 库里面不仅仅有地理编码,还有其他很多几何计算相关的库。地理编码只是其中的一小部分。本文没有介绍到的 S2 的实现还有很多很多,各种向量计算,面积计算,多边形覆盖,距离问题,球面球体上的问题,它都有实现。
S2 还能解决多边形覆盖的问题。比如给定一个城市,求一个多边形刚刚好覆盖住这个城市。
6.S2使用工具类
主要包含3类方法:
- getS2RegionByXXX
获取给定经纬度坐标对应的S2Region,该region可用于获取cellId,或用于判断包含关系 - getCellIdList
获取给定region的cellId,并通过childrenCellId方法控制其严格遵守minLevel - contains
对于指定S2Region,判断经纬度或CellToken是否在其范围内
1)WGS84Point类,存经纬度
package com.leo.test.sd; public class WGS84Point { private Double latitude; private Double longitude; public Double getLatitude() { return latitude; } public WGS84Point setLatitude(Double latitude) { this.latitude = latitude; return this; } public Double getLongitude() { return longitude; } public WGS84Point setLongitude(Double longitude) { this.longitude = longitude; return this; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
2)Tuple2自定义元组,存经纬度
package com.leo.test.sd; public class Tuple2<A, B> { private A a; private B b; public static Tuple2<Double, Double> tuple(Double a, Double b) { Tuple2 tuple2 = new Tuple2(); tuple2.setA(a); tuple2.setB(b); return tuple2; } private void setA(A a) { this.a = a; } private void setB(B b) { this.b = b; } public A getVal1() { return a; } public B getVal2() { return b; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
3)S2Util,部分API示例
package com.leo.test.sd; import com.google.common.collect.Lists; import com.google.common.geometry.*; import java.util.List; import java.util.stream.Collectors; public enum S2Util { /** * 实例 */ INSTANCE; private static int minLevel = 11; private static int maxLevel = 16; private static int maxCells = 100; private static final S2RegionCoverer COVERER = new S2RegionCoverer(); static { COVERER.setMinLevel(minLevel); COVERER.setMaxLevel(maxLevel); COVERER.setMaxCells(maxCells); } /** * 将单个cellId转换为多个指定level的cellId * @param s2CellId * @param desLevel * @return */ public static List<S2CellId> childrenCellId(S2CellId s2CellId, Integer desLevel) { return childrenCellId(s2CellId, s2CellId.level(), desLevel); } private static List<S2CellId> childrenCellId(S2CellId s2CellId, Integer curLevel, Integer desLevel) { if (curLevel < desLevel) { long interval = (s2CellId.childEnd().id() - s2CellId.childBegin().id()) / 4; List<S2CellId> s2CellIds = Lists.newArrayList(); for (int i = 0; i < 4; i++) { long id = s2CellId.childBegin().id() + interval * i; s2CellIds.addAll(childrenCellId(new S2CellId(id), curLevel + 1, desLevel)); } return s2CellIds; } else { return Lists.newArrayList(s2CellId); } } /** * 将cellToken转换为经纬度 * @param token * @return */ public static Tuple2<Double, Double> toLatLon(String token) { S2LatLng latLng = new S2LatLng(S2CellId.fromToken(token).toPoint()); return Tuple2.tuple(latLng.latDegrees(), latLng.lngDegrees()); } /** * 将经纬度转换为cellId * @param lat * @param lon * @return */ public static S2CellId toCellId(double lat, double lon) { return S2CellId.fromLatLng(S2LatLng.fromDegrees(lat, lon)); } /** * 判断region是否包含指定cellToken * @param region * @param cellToken * @return */ public static boolean contains(S2Region region, String cellToken) { return region.contains(new S2Cell(S2CellId.fromToken(cellToken))); } /** * 判断region是否包含指定经纬度坐标 * @param region * @param lat * @param lon * @return */ public static boolean contains(S2Region region, double lat, double lon) { S2LatLng s2LatLng = S2LatLng.fromDegrees(lat, lon); try { boolean contains = region.contains(new S2Cell(s2LatLng)); return contains; } catch (NullPointerException e) { e.printStackTrace(); return false; } } /** * 根据region获取cellId列表 * @param region * @return */ public static List<S2CellId> getCellIdList(S2Region region) { List<S2CellId> primeS2CellIdList = COVERER.getCovering(region).cellIds(); return primeS2CellIdList.stream().flatMap(s2CellId -> S2Util.childrenCellId(s2CellId, S2Util.minLevel).stream()).collect(Collectors.toList()); } /** * 根据region获取合并后的cellId列表 * @param region * @return */ public static List<S2CellId> getCompactCellIdList(S2Region region) { List<S2CellId> primeS2CellIdList = COVERER.getCovering(region).cellIds(); return primeS2CellIdList; } //获取圆形region public static S2Region getS2RegionByCircle(double lat, double lon, double radius) { double capHeight = (2 * S2.M_PI) * (radius / 40075017); S2Cap cap = S2Cap.fromAxisHeight(S2LatLng.fromDegrees(lat, lon).toPoint(), capHeight * capHeight / 2); S2CellUnion s2CellUnion = COVERER.getCovering(cap); return cap; } public static S2Region getS2RegionByCircle(WGS84Point point, double radius) { return getS2RegionByCircle(point.getLatitude(), point.getLongitude(), radius); } //获取矩形region public static S2Region geS2RegionByRect(WGS84Point point1, WGS84Point point2) { return getS2RegionByRect(point1.getLatitude(), point1.getLongitude(), point2.getLatitude(), point2.getLongitude()); } public static S2Region getS2RegionByRect(Tuple2<Double, Double> point1, Tuple2<Double, Double> point2) { return getS2RegionByRect(point1.getVal1(), point1.getVal2(), point2.getVal1(), point2.getVal2()); } public static S2Region getS2RegionByRect(double lat1, double lon1, double lat2, double lon2) { List<Tuple2<Double, Double>> latLonTuple2List = Lists.newArrayList(Tuple2.tuple(lat1, lon1), Tuple2.tuple(lat1, lon2), Tuple2.tuple(lat2, lon2), Tuple2.tuple(lat2, lon1)); return getS2RegionByPolygon(latLonTuple2List); } //获取多边形region public static S2Region getS2RegionByPolygon(WGS84Point[] pointArray) { List<Tuple2<Double, Double>> latLonTuple2List = Lists.newArrayListWithExpectedSize(pointArray.length); for (int i = 0; i < pointArray.length; ++i) { latLonTuple2List.add(Tuple2.tuple(pointArray[i].getLatitude(), pointArray[i].getLongitude())); } return getS2RegionByPolygon(latLonTuple2List); } public static S2Region getS2RegionByPolygon(Tuple2<Double, Double>[] tuple2Array) { return getS2RegionByPolygon(Lists.newArrayList(tuple2Array)); } /** * 注意需要以逆时针方向添加坐标点,多边形内部区域 */ public static S2Region getS2RegionByPolygon(List<Tuple2<Double, Double>> latLonTuple2List) { List<S2Point> pointList = Lists.newArrayList(); for (Tuple2<Double, Double> latlonTuple2 : latLonTuple2List) { pointList.add(S2LatLng.fromDegrees(latlonTuple2.getVal1(), latlonTuple2.getVal2()).toPoint()); } S2Loop s2Loop = new S2Loop(pointList); S2Polygon s2Polygon = new S2Polygon(s2Loop); return s2Polygon; /* S2PolygonBuilder builder = new S2PolygonBuilder(S2PolygonBuilder.Options.DIRECTED_XOR); builder.addLoop(s2Loop); return builder.assemblePolygon(); * */ } //配置coverer参数 public static int getMinLevel() { return minLevel; } public static void setMinLevel(int minLevel) { S2Util.minLevel = minLevel; COVERER.setMinLevel(minLevel); } public static int getMaxLevel() { return maxLevel; } public static void setMaxLevel(int maxLevel) { S2Util.maxLevel = maxLevel; COVERER.setMaxLevel(maxLevel); } public static int getMaxCells() { return maxCells; } public static void setMaxCells(int maxCells) { S2Util.maxCells = maxCells; COVERER.setMaxCells(maxCells); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
4)TestS2Util测试类
package com.leo.test.sd; import com.google.common.collect.Lists; import com.google.common.collect.Maps; import com.google.common.geometry.S2CellId; import com.google.common.geometry.S2LatLng; import com.google.common.geometry.S2LatLngRect; import com.google.common.geometry.S2Region; import java.util.List; import java.util.Map; public class TestS2Util { public static void main(String[] args) { getCellIdListByPolygon(); // getCellIdListByCircle(); //构造一个矩形区域,判断该点是否在区域内 S2LatLng startS2 = S2LatLng.fromDegrees(0.8293, 72.004); //左下角 S2LatLng endS2 = S2LatLng.fromDegrees(55.8271, 137.8347); //右上角 S2LatLngRect rect = new S2LatLngRect(startS2, endS2); boolean contains = rect.contains(S2LatLng.fromDegrees(30, 110).toPoint()); System.out.println(contains); } public static void getCellIdListByCircle() { Map<Integer,Integer> sizeCountMap= Maps.newHashMap(); StringBuilder sb3=new StringBuilder(); S2Region s2Region = S2Util.getS2RegionByCircle(23.753954,120.749615,193511.10); List<S2CellId> cellIdListByPolygon = S2Util.getCompactCellIdList(s2Region); cellIdListByPolygon.forEach(s2CellId -> { System.out.println("Level:" + s2CellId.level() + ",ID:" + s2CellId.toToken() + ",Min:" + s2CellId.rangeMin().toToken() + ",Max:" + s2CellId.rangeMax().toToken()); sb3.append(",").append(s2CellId.toToken()); sizeCountMap.put(s2CellId.level(),sizeCountMap.getOrDefault(s2CellId.level(),0)+1); }); System.out.println(sb3.substring(1)); System.out.println("totalSize:"+cellIdListByPolygon.size()); sizeCountMap.entrySet().forEach(integerIntegerEntry -> { System.out.printf("level:%d,size:%d\n",integerIntegerEntry.getKey(),integerIntegerEntry.getValue()); }); } public static void getCellIdListByPolygon() { Map<Integer,Integer> sizeCountMap= Maps.newHashMap(); StringBuilder sb3=new StringBuilder(); S2Region s2Region = S2Util.getS2RegionByPolygon(Lists.newArrayList(Tuple2.tuple(23.851458634747043, 113.66432546548037), Tuple2.tuple(21.60205563594303, 114.82887624673037),Tuple2.tuple(23.771049234941454, 116.18019460610537),Tuple2.tuple(23.16640234327511, 114.94423269204286))); //大小相同的格子 // List<S2CellId> cellIdListByPolygon = S2Util.getCellIdList(s2Region); //如果调用的是getCompactCellIdList,则结果如下,其cell数从1000多压缩到200多,按照设置的精度合并 List<S2CellId> cellIdListByPolygon = S2Util.getCompactCellIdList(s2Region); cellIdListByPolygon.forEach(s2CellId -> { System.out.println("Level:" + s2CellId.level() + ",ID:" + s2CellId.toToken() + ",Min:" + s2CellId.rangeMin().toToken() + ",Max:" + s2CellId.rangeMax().toToken()); sb3.append(",").append(s2CellId.toToken()); sizeCountMap.put(s2CellId.level(),sizeCountMap.getOrDefault(s2CellId.level(),0)+1); }); System.out.println(sb3.substring(1)); System.out.println("totalSize:"+cellIdListByPolygon.size()); sizeCountMap.entrySet().forEach(integerIntegerEntry -> { System.out.printf("level:%d,size:%d\n",integerIntegerEntry.getKey(),integerIntegerEntry.getValue()); }); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
7.S2精度表
| level | min area | max area | average area | units | Random cell 1 (UK) min edge length | Random cell 1 (UK) max edge length | Random cell 2 (US) min edge length | Random cell 2 (US) max edge length | Number of cells |
|---|---|---|---|---|---|---|---|---|---|
| 00 | 85011012.19 | 85011012.19 | 85011012.19 | km2 | 7842 km | 7842 km | 7842 km | 7842 km | 6 |
| 01 | 21252753.05 | 21252753.05 | 21252753.05 | km2 | 3921 km | 5004 km | 3921 km | 5004 km | 24 |
| 02 | 4919708.23 | 6026521.16 | 5313188.26 | km2 | 1825 km | 2489 km | 1825 km | 2489 km | 96 |
| 03 | 1055377.48 | 1646455.50 | 1328297.07 | km2 | 840 km | 1167 km | 1130 km | 1310 km | 384 |
| 04 | 231564.06 | 413918.15 | 332074.27 | km2 | 432 km | 609 km | 579 km | 636 km | 1536 |
| 05 | 53798.67 | 104297.91 | 83018.57 | km2 | 210 km | 298 km | 287 km | 315 km | 6K |
| 06 | 12948.81 | 26113.30 | 20754.64 | km2 | 108 km | 151 km | 143 km | 156 km | 24K |
| 07 | 3175.44 | 6529.09 | 5188.66 | km2 | 54 km | 76 km | 72 km | 78 km | 98K |
| 08 | 786.20 | 1632.45 | 1297.17 | km2 | 27 km | 38 km | 36 km | 39 km | 393K |
| 09 | 195.59 | 408.12 | 324.29 | km2 | 14 km | 19 km | 18 km | 20 km | 1573K |
| 10 | 48.78 | 102.03 | 81.07 | km2 | 7 km | 9 km | 9 km | 10 km | 6M |
| 11 | 12.18 | 25.51 | 20.27 | km2 | 3 km | 5 km | 4 km | 5 km | 25M |
| 12 | 3.04 | 6.38 | 5.07 | km2 | 1699 m | 2 km | 2 km | 2 km | 100M |
| 13 | 0.76 | 1.59 | 1.27 | km2 | 850 m | 1185 m | 1123 m | 1225 m | 402M |
| 14 | 0.19 | 0.40 | 0.32 | km2 | 425 m | 593 m | 562 m | 613 m | 1610M |
| 15 | 47520.30 | 99638.93 | 79172.67 | m2 | 212 m | 296 m | 281 m | 306 m | 6B |
| 16 | 11880.08 | 24909.73 | 19793.17 | m2 | 106 m | 148 m | 140 m | 153 m | 25B |
| 17 | 2970.02 | 6227.43 | 4948.29 | m2 | 53 m | 74 m | 70 m | 77 m | 103B |
| 18 | 742.50 | 1556.86 | 1237.07 | m2 | 27 m | 37 m | 35 m | 38 m | 412B |
| 19 | 185.63 | 389.21 | 309.27 | m2 | 13 m | 19 m | 18 m | 19 m | 1649B |
| 20 | 46.41 | 97.30 | 77.32 | m2 | 7 m | 9 m | 9 m | 10 m | 7T |
| 21 | 11.60 | 24.33 | 19.33 | m2 | 3 m | 5 m | 4 m | 5 m | 26T |
| 22 | 2.90 | 6.08 | 4.83 | m2 | 166 cm | 2 m | 2 m | 2 m | 105T |
| 23 | 0.73 | 1.52 | 1.21 | m2 | 83 cm | 116 cm | 110 cm | 120 cm | 422T |
| 24 | 0.18 | 0.38 | 0.30 | m2 | 41 cm | 58 cm | 55 cm | 60 cm | 1689T |
| 25 | 453.19 | 950.23 | 755.05 | cm2 | 21 cm | 29 cm | 27 cm | 30 cm | 7e15 |
| 26 | 113.30 | 237.56 | 188.76 | cm2 | 10 cm | 14 cm | 14 cm | 15 cm | 27e15 |
| 27 | 28.32 | 59.39 | 47.19 | cm2 | 5 cm | 7 cm | 7 cm | 7 cm | 108e15 |
| 28 | 7.08 | 14.85 | 11.80 | cm2 | 2 cm | 4 cm | 3 cm | 4 cm | 432e15 |
| 29 | 1.77 | 3.71 | 2.95 | cm2 | 12 mm | 18 mm | 17 mm | 18 mm | 1729e15 |
| 30 | 0.44 | 0.93 | 0.74 | cm2 | 6 mm | 9 mm | 8 mm | 9 mm | 7e18 |




