python NSGA-II 算法_nsga2算法python

NSGA-II 算法

NSGA-II 提出的 NSGA的缺点

• 算法计算量大。NSGA算法的计算复杂度与种群数量N、目标函数个数m的关系为T = O(mN3)，当种群规模较大、目标函数较多时所耗时间较长。
• 没有应用精英策略。未通过精英策略提高优秀个体的保留概率，因而无法加快程序的执行速度
• 需要人为地指定共享半径σshare，对于经验的要求非常高。

为了改善NSGA算法的缺点，Deb等人在2002年提出了NSGA-II算法[44]。相对于NSGA算法，NSGA-II算法主要在以下三个方面做了改进：

（1）NSGA-II算法使用了快速非支配排序法，将算法的计算复杂度由O(mN3)降到了O(mN2)，使得算法的计算时间大大减少。

（2）采用了精英策略，将父代个体与子代个体合并后进行非支配排序，使得搜索空间变大，生成下一代父代种群时按顺序将优先级较高的个体选入，并在同级个体中采用拥挤度进行选择，保证了优秀个体能够有更大的概率被保留。
（3）用拥挤度的方法代替了需指定共享半径的适应度共享策略，并作为在同级个体中选择优秀个体的标准，保证了种群中个体的多样性，有利于个体能够在整个区间内进行选择、交叉和变异。

实践证明，NSGA-II算法无论在优化效果还是运算时间等方面都比NSGA算法有了一定的改进，是一种优秀的多目标优化算法。

快速非支配排序

快速非支配排序是在Pareto支配基础上提出的概念。假设有k个目标函数记为fi (x)，其中i是1, 2, … , k中的任意整数，j同样是1,2, …, k中的任意整数，但i≠j。若个体x1和x2对于任意的目标函数都有fi(x1) < fi(x2)则称个体x1支配x2；若对于任意的目标函数都有fi(x1) ≤ fi(x2)且至少有一个目标函数使得fj(x1) < fj(x2)成立则称x1弱支配x2；若既存在目标函数使得fi(x1) ≤ fi(x2)成立又存在目标函数满足fj(x1) > fj(x2)，则称个体x1和x2互不支配。

种群中的每个个体都有两个参数ni和Si，ni为种群中支配个体i 的个体数量，Si是被个体i支配的个体的集合,快速非支配排序的步骤如下：

（1）通过循环比较找到种群中所有ni = 0的个体，赋予其非支配等级为1，并将这些个体存入非支配集合rank1中。

（2）集合rank1中的每一个个体，将其所支配的个体集合中的每个个体的nj都减去1，若nj-1=0则将个体j存入集合rank2中，并赋予其中的个体非支配等级2。

（3）之后对rank2中的个体重复上述操作，直至所有个体都被赋予了非支配等级。

非支配等级也称作Pareto等级，其中Pareto等级为1的个体由于不受其他个体的支配，叫做非支配解，也叫 Pareto最优解，而解集所形成的曲线叫做Pareto前沿

对于二目标优化问题来讲, 支配的含义在于 解A的值在两个目标函数上都优与解B , 这样我们就称 解A支配解B

选择操作首先考虑第一层非支配集，按照某种策略从第一层中选取个体;然后再考虑在第二层非支配个体集合中选择个体，依此类推,直至满足新进化群体的大小要求。

拥挤度与拥挤度比较算子

1) 拥挤度计算公式

2) 拥挤比较算子

算法步骤

第一步：初始种群并设置进化代数Gen=1。

第二步：判断是否生成了第一代子种群，若已生成则令进化代数Gen=2，否则，对初始种群进行非支配排序和选择、高斯交叉、变异从而生成第一代子种群并使进化代数Gen=2。

第三步：将父代种群与子代种群合并为新种群。

第四步：判断是否已生成新的父代种群，若没有则计算新种群中个体的目标函数，并执行快速非支配排序、计算拥挤度、精英策略等操作生成新的父代种群；否则，进入第五步。

第五步：对生成的父代种群执行选择、交叉、变异操作生成子代种群。

第六步：判断Gen是否等于最大的进化代数，若没有则进化代数Gen=Gen+1并返回第三步；否则，算法运行结束

python 实现

import geatpy as ea
import numpy as np
class MyProblem(ea.Problem):  # 继承Problem父类
	def __init__(self):
    	name = 'NSGA2算法'  # 初始化name（函数名称，可以随意设置）
    	M = 2  # 优化目标个数（两个x)
    	maxormins = [1] * M  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
    	Dim = 1  # 初始化Dim（决策变量维数）
    	varTypes = [0]  # 初始化varTypes（决策变量的类型，0：实数；1：整数）
    	lb = [-10]  # 决策变量下界(自定义个上下界搜索)
    	ub = [10]  # 决策变量上界
    	lbin = [1]  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
    	ubin = [1]  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
    	# 调用父类构造方法完成实例化
    	ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

	def evalVars(self, Vars):  # 目标函数
    	f1 = Vars ** 2 # 第一个目标函数
    	f2 = (Vars - 2) ** 2 # 第二个目标函数
    	ObjV = np.hstack([f1, f2])  # 计算目标函数值矩阵
    	CV = -Vars ** 2 + 2.5 * Vars - 1.5  # 构建违反约束程度矩阵（需要转换为小于，反转一下）
    	return ObjV, CV

# 实例化问题对象
problem = MyProblem()
# 构建算法
algorithm = ea.moea_NSGA2_templet(problem,
	                              # RI编码，种群个体50
    	                            ea.Population(Encoding='RI', NIND=50),
        	                        MAXGEN=200,  # 最大进化代数
            	                    logTras=1)  # 表示每隔多少代记录一次日志信息，0表示不记录。
# 求解
res = ea.optimize(algorithm, seed=1, verbose=False, drawing=1, outputMsg=True, drawLog=False, saveFlag=False, dirName='result')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

后会在一个result文件夹里看到多个帕累托最优解，这个时候就要根据自己的决策了

帕累托最优解

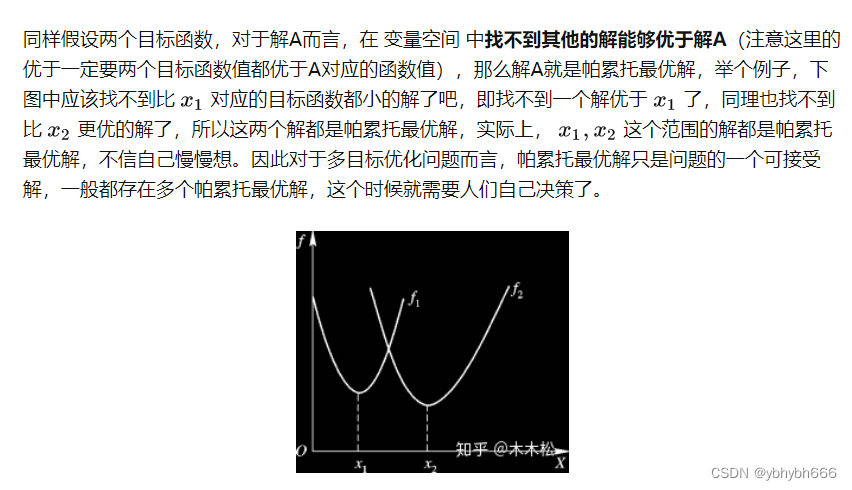
parero寻优类似于推荐系统，简单来说就是系统没有决定权，只有建议权。所以系统会推荐一系列在当前评价函数下性能相似的解。这个时候就需要决策者使用决定权从这些解中选择一个。如果是理论问题的话，最简单的就是随机选一个，反正都一样。但是到了实际问题，那就得具体问题具体分析了。比如，一次期末考试，考数学，语文和英语（三个评价函数），那么系统就会推荐你这三科分别的第一（parero 最优），然后让你从中间选一个最好的，你会怎么选？如果你是个普通老师，你会选总分最高的。但是如果你是一个数学竞赛的老师，你会选一个数学最高的那个。归根到底，还是那句话，具体问题具体分析。