- 1node.js后端框架介绍_node.js后端框架及作用
- 2【ubuntu20.04上openvino安装及环境配置】_[setupvars.sh] openvino environment initialized
- 3python requests post线程安全_关于python requests库中session线程安全方面问题的小疑问...
- 4怎么防止跨站脚本攻击(XSS)?
- 5送给女朋友表白的小爱心,用Python这样画就对了_python 手机点开文件显示python的爱心效果
- 6小布助手,身入大千世界
- 7Attension注意力机制综述(一)——自注意力机制self_attention(含代码)_attension计算公式
- 8postgresql 查找慢sql之二: pg_stat_statements_可以使用pg_stat_statements去查询运行时间长的sql语句。
- 9传统行业被裁,奋战一年成功逆袭!做好这四个环节,轻轻松松斩下腾讯Offer!
- 10js之es新特性
Python数据分析——上海市二手房价格分析_python房价数据分析及预测的毕业设计亮点是
赞
踩
自学数据分析与机器学习已有两月,近期房价问题引人深思,即兴做个上海市房价的数据分析小项目。上网一查上海市新楼盘价格,高的不忍直视,索性退而求其次,分析上海二手房的价格。
一、数据收集
常规做法是编写网络爬虫程序,爬取相关网站的数据信息。捷径是用八爪鱼爬虫软件爬取房天下、安居客等网站的二手房信息。
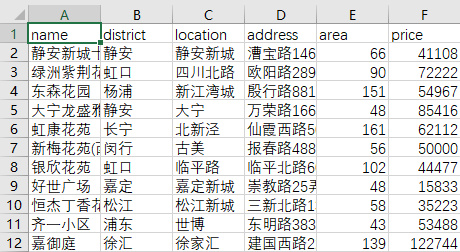
二、数据准备
不同网站上爬取的数据信息差异较大,这里仅保留共有的信息,其中重要信息为行政区划(district)、具体地址(address)、房屋面积(area)和房屋价格(price),其中房屋价格为每平方米单价,最终数据量为3423条。
三、初步分析
1、整体房价分析
首先对上海市的整体房价进行处理,包括平均价格、中位数价格和价格分布:
- import pandas as pd
- import matplotlib.pyplot as plt
- from pylab import mpl
- mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
- mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
-
- #读取本地数据
- house = pd.read_csv('house_price.csv', encoding='gbk')
-
- #输出上海市二手房的最高价格、最低价格、平均价格和中位数价格
- price = house['price']
- max_price = price.max()
- min_price = price.min()
- mean_price = price.mean()
- median_price = price.median()
-
- print("上海市二手房最高价格:%.2f元/平方米" %max_price)
- print("上海市二手房最低价格:%.2f元/平方米" %min_price)
- print("上海市二手房平均价格:%.2f元/平方米" %mean_price)
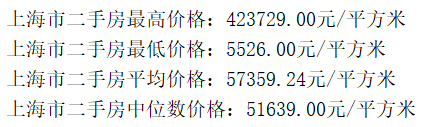
- print("上海市二手房中位数价格:%.2f元/平方米" %median_price)

从统计结果上来看,上海二手房最高价格超过40万元/平方米,最低价格不高于6千元/平方米,差异极大。房价的平均数和中位数均在5-6万元/平方米。接下来展示整体二手房价的分布:
- #绘制房价分布直方图
- plt.xlim(0,450000)
- plt.ylim(0,500)
- plt.title("上海市二手房价格分析")
- plt.xlabel("二手房价格 (元/平方米)")
- plt.ylabel("二手房数量")
- plt.hist(price, bins=60)
- plt.vlines(mean_price, 0, 500, color='red', label='平均价格', linewidth=1.5, linestyle='--')
- plt.vlines(median_price, 0, 500, color='red',label='中位数价格', linewidth=1.5)
- plt.legend()
- plt.show()
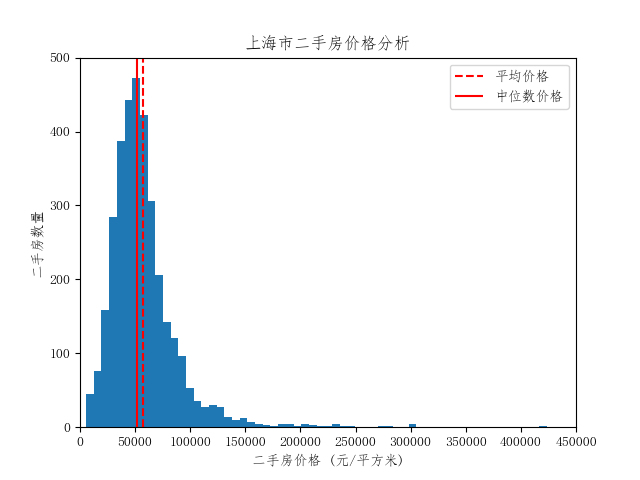
从二手房价的整体分布来看,其数据分布类似于正态分布,呈现单峰特点,且平均值和中位数十分接近峰值。
2、影响房价的因素分析
单纯分析房价数据意义不明显,需要重点分析影响房价的因素。本项目中重点讨论地理位置和房屋类型对房价的影响。这里采用行政区划(district)作为地理位置的影响因素,采用房屋面积(area)作为房屋类型的影响因素。
(1)行政区划对房价的影响
首先分析各行政区划内的平均房价,并进行排序:
- #各行政区划内房价的平均值及其排序
- mean_price_district = house.groupby('district')['price'].mean().sort_values(ascending=False)
- mean_price_district.plot(kind='bar',color='b')
- print(mean_price_district)
- plt.ylim(10000,100000,10000)
- plt.title("上海市各行政区划二手房平均价格分析")
- plt.xlabel("上海市行政区划")
- plt.ylabel("二手房平均价格(元/平方米)")
- plt.show()
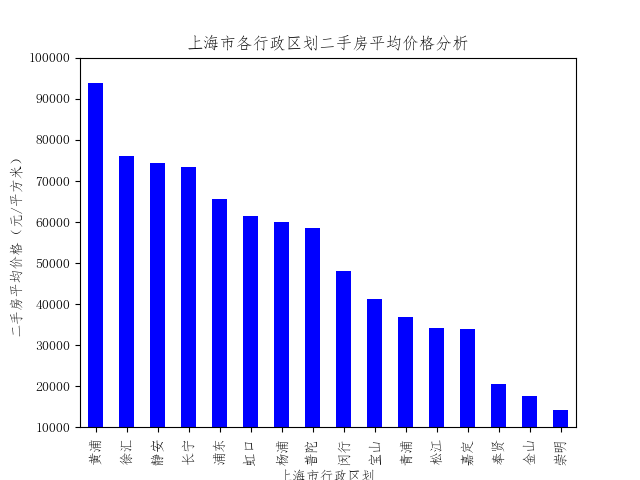
可以看出黄浦区的均价最贵,超过9万元/平方米,接下来是徐汇、静安和长宁,三者房价比较接近,在7-8万元/平方米的区间内。对比上海中心城区名单(黄浦、静安、徐汇、长宁、虹口、杨浦、普陀以及浦东新区的外环内城区),可以发现房价分布与中心城区十分符合。
1个亿万富翁和9个穷人平均一下可以获得10个千万富翁。因此有必要查看各行政区划内的房价分布,这里作出各区的房价箱形图:
- #上海市各行政区划二手房价格箱形图
- house.boxplot(column='price', by='district', whis=1.5,)
- plt.title("上海市各行政区划二手房价格分析(箱形图)")
- plt.show()
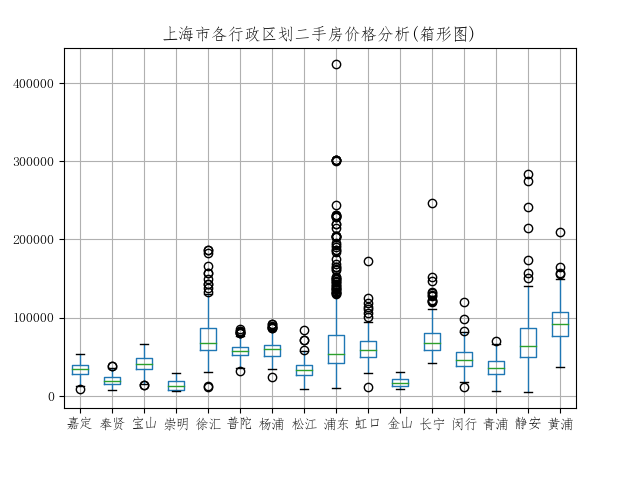
箱型图具有较强的数据分布检查和异常值检查功能。从上海各行政区划二手房价格的箱型图可以看出,上海几个传统的中心城区(黄浦、徐汇、静安、长宁等)具有较多上侧异常值,其中浦东最多。这与常识相符,如靠近知名商圈或豪宅小区的房价会特别贵。相反,上海的周边区划异常值极少,房价分布区间相对较小。
(2)房屋面积对房价的影响
接下来分析房屋面积对房价的影响。房屋面积在一定程度上反映了房屋类型。例如面积超过200平方米的房子很有可能是别墅或者复式结构住宅,此类房屋往往在优质住宅区内,价格很有可能偏高。
首先查看房价随房屋面积的分布,采用散点图进行可视化:
- #房屋面积与房价的关系——散点图
- x = house['area']
- y = house['price']
- plt.scatter(x,y,s=2.5)
- plt.title("房屋面积对二手房价的影响")
- plt.show()
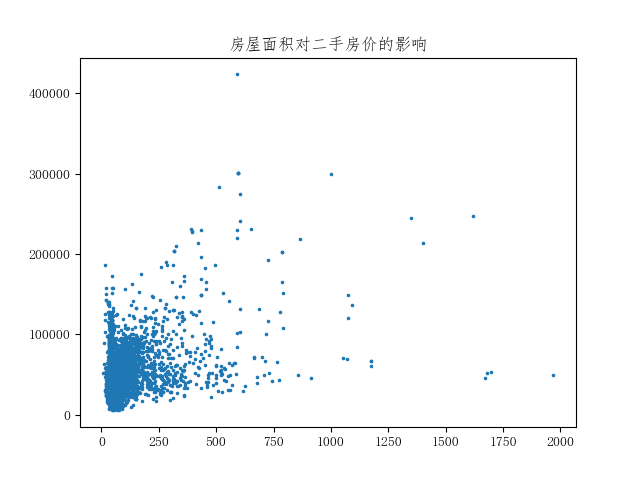
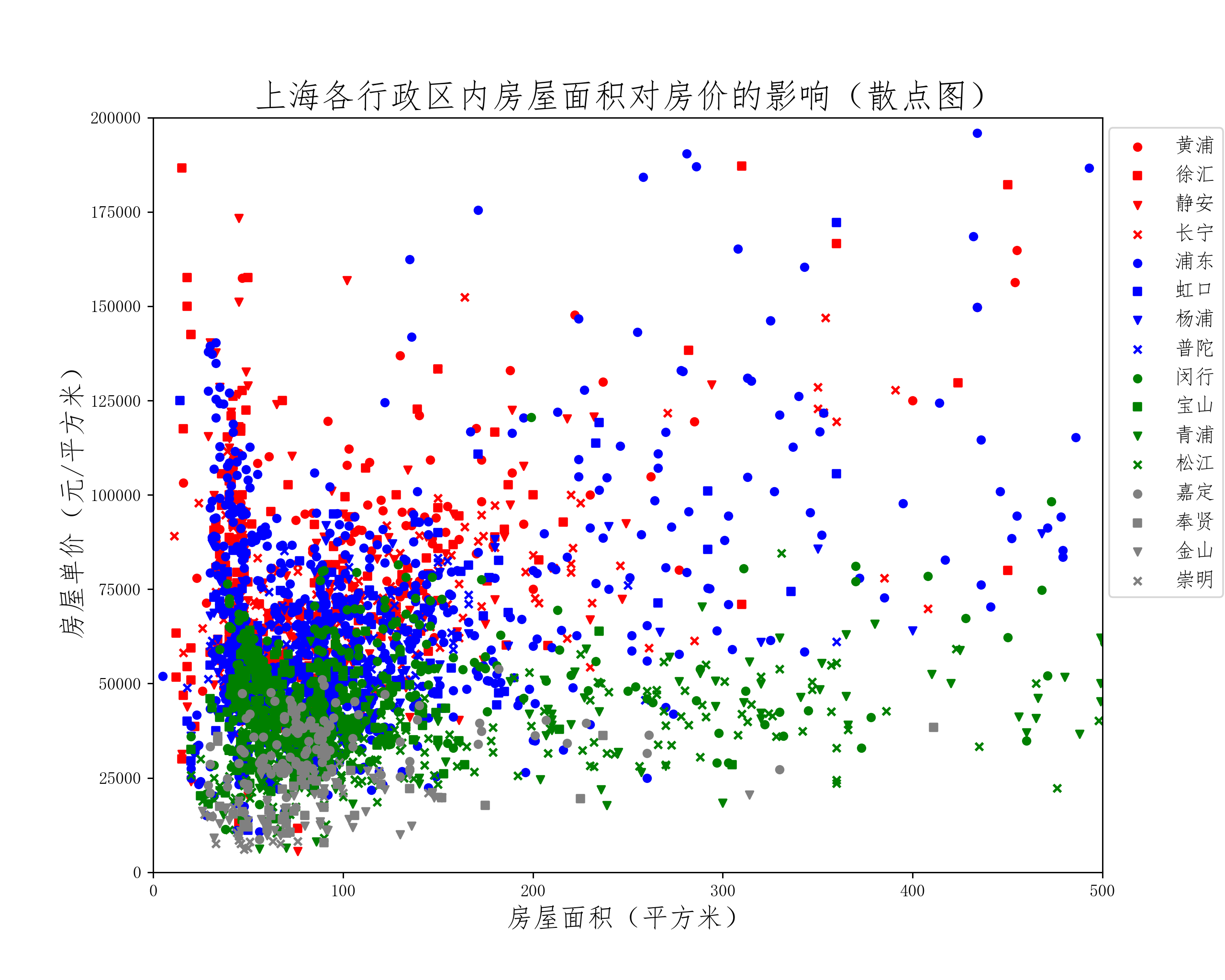
全部数据的散点图分布很乱,看不到明显的规律。结合前面对行政区划的分析,自然想到16个行政区内房价应该存在不同的分布规律,因此有必要区分各个行政区划:
- def plot_scatter():
- plt.figure(figsize=(10,8),dpi=256)
- colors = ['red', 'red', 'red', 'red',
- 'blue', 'blue', 'blue', 'blue',
- 'green', 'green', 'green', 'green',
- 'gray', 'gray', 'gray', 'gray']
- district = ['黄浦','徐汇','静安','长宁',
- '浦东', '虹口', '杨浦', '普陀',
- '闵行', '宝山', '青浦', '松江',
- '嘉定', '奉贤', '金山', '崇明']
- markers = ['o','s','v','x',
- 'o', 's', 'v', 'x',
- 'o', 's', 'v', 'x',
- 'o', 's', 'v', 'x']
- print(district)
- for i in range(16):
- x = house.loc[house['district'] == district[i]]['area']
- y = house.loc[house['district'] == district[i]]['price']
- plt.scatter(x, y, c=colors[i], s=20, label=district[i], marker=markers[i])
-
-
- plt.legend(loc=1,bbox_to_anchor=(1.138,1.0),fontsize=12)
- plt.xlim(0,500)
- plt.ylim(0,200000)
- plt.title('上海各行政区内房屋面积对房价的影响(散点图)',fontsize=20)
- plt.xlabel('房屋面积(平方米)',fontsize=16)
- plt.ylabel('房屋单价(元/平方米)',fontsize=16)
- plt.show()
-
- plot_scatter()

为了体现各区房价分布的区别,将作图范围缩小,仍包含绝大部分数据。图例按照平均房价的顺序排列,红色为价格第一梯队,蓝色为价格第二梯队,绿色为价格第三梯队,灰色为价格第四梯队,每个梯度包含四个行政区划。从散点图中可以明显观察到第一梯队的红色散点相对偏向左上方,各个梯队相比于上一梯队整体向下偏移。
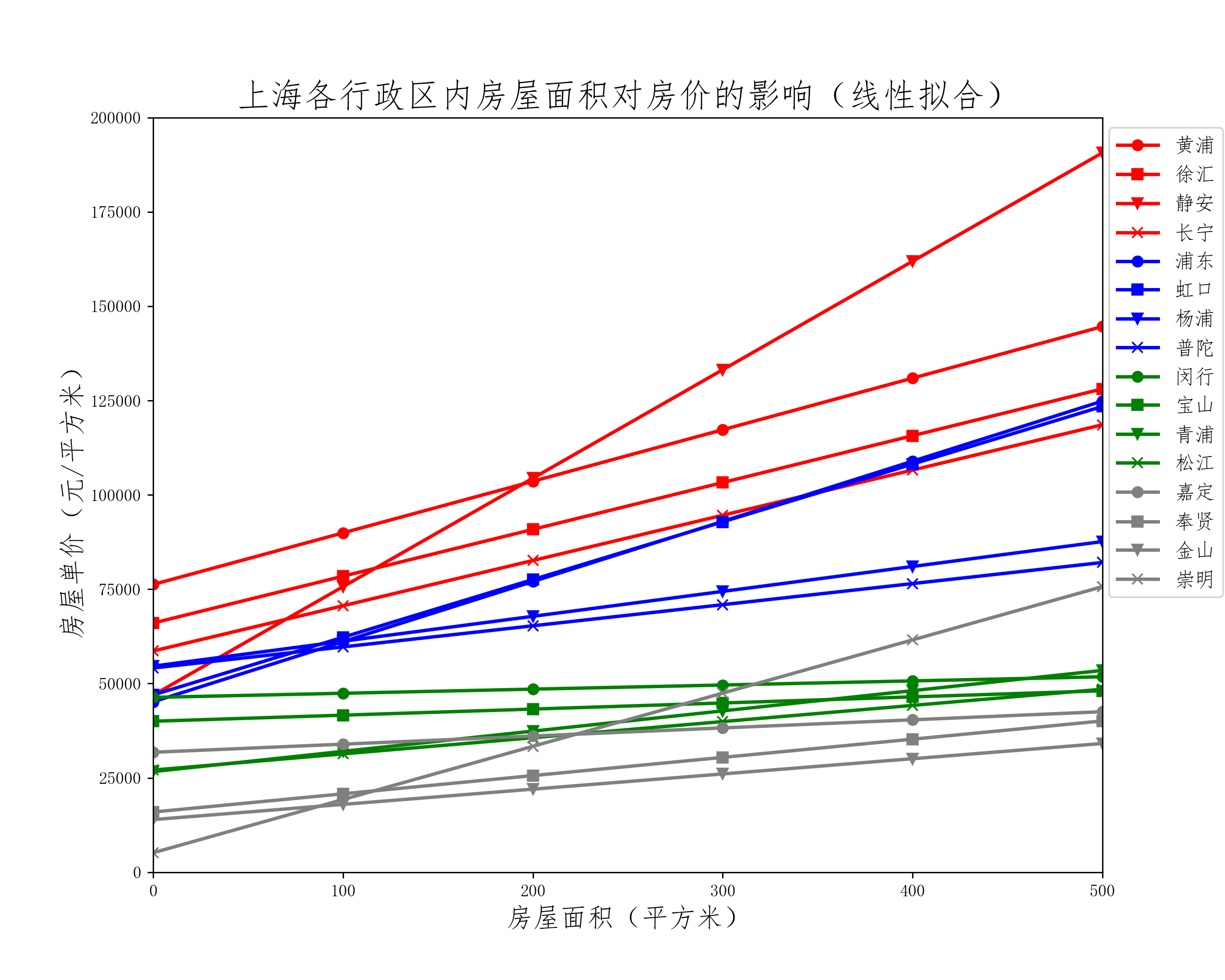
为了更明显地比较各行政区房屋面积对房价影响规律,对各区的散点进行最小二乘线性拟合:
- #导入优化模块,作线性拟合
- from scipy import optimize
- #直线函数方程
- def linearfitting(x, A, B):
- return A*x + B
-
- def plot_line():
- plt.figure(figsize=(10,8),dpi=256)
- colors = ['red', 'red', 'red', 'red',
- 'blue', 'blue', 'blue', 'blue',
- 'green', 'green', 'green', 'green',
- 'gray', 'gray', 'gray', 'gray']
- district = ['黄浦','徐汇','静安','长宁',
- '浦东', '虹口', '杨浦', '普陀',
- '闵行', '宝山', '青浦', '松江',
- '嘉定', '奉贤', '金山', '崇明']
- markers = ['o','s','v','x',
- 'o', 's', 'v', 'x',
- 'o', 's', 'v', 'x',
- 'o', 's', 'v', 'x']
-
- for i in range(16):
- x = house.loc[house['district'] == district[i]]['area']
- y = house.loc[house['district'] == district[i]]['price']
- A, B = optimize.curve_fit(linearfitting, x, y)[0]
- xx = np.arange(0, 2000, 100)
- yy = A * xx + B
- plt.plot(xx, yy, c=colors[i], marker=markers[i],label=district[i],linewidth=2)
-
-
- plt.legend(loc=1,bbox_to_anchor=(1.138,1.0),fontsize=12)
- plt.xlim(0,500)
- plt.ylim(0,200000)
- plt.title('上海各行政区内房屋面积对房价的影响(线性拟合)',fontsize=20)
- plt.xlabel('房屋面积(平方米)',fontsize=16)
- plt.ylabel('房屋单价(元/平方米)',fontsize=16)
- plt.show()
-
- plot_line()

从线性拟合结果上来看,房价随房屋面积的变化规律与预期相符,即平均房价越高的行政区划内,其房价随房屋面积变化的回归线越偏向左上方。仅静安区和崇明区存在例外,其回归线的斜率较高:在房屋面积小时其价格较低,符合预期;但随着房屋面积增大,特别是超过200平方米后其价格急剧上升。造成这种情况主要是由于样本量较少,所以一部分异常数据会显著改变线性拟合结果。
四、深入分析
经过初步分析,大致了解了各行政区划内房价的平均水平及房屋面积对房价的影响规律。然而,在同一行政区划内房屋价格的差异巨大,特别是上海中心城区,这与其具体的地理位置密切相关。
1、房价数据地图(热力图)
为了进一步挖掘地理位置对房价的影响,我们引入百度地图工具,对房价进行深入分析。首先,注册百度开发者,申请密钥,编写根据房屋具体地址通过百度地图获取其经纬度的模块:
- #应用百度地图API获取各个房屋的经纬度信息
- from bs4 import BeautifulSoup
- import requests
- import json
-
- class Html(object):
- soup = None
-
- def __init__(self,address):
- url0 = 'http://api.map.baidu.com/geocoder/v2/?address='
- ak = '你所申请的ak'
- self.address = address
- city = '上海市'
- baiduAPI_url = url0 + address + '&city=' + city + '&output=json&pois=1&ak=' + ak
- html = requests.get(baiduAPI_url).content # 获取查询页的html
- self.soup = BeautifulSoup (html, 'lxml') # 得到soup对象
-
- def get_location(self):
- response = self.soup.select('p')[0].get_text()
- response = json.loads(response)
- try:
- lng = response['result']['location']['lng']
- lat = response['result']['location']['lat']
- except BaseException:
- return 0,0
- else:
- return lng,lat

调用该模块获取所有房屋的经纬度:
- from Project_HousePrice.BaiduAPI import Html
- house = pd.read_csv('house_price.csv', encoding='gbk')
- address = house['address']
-
- #创建空列表coord,用来存储房屋的坐标(经纬度)
- coord = []
- #循环遍历每个房屋的具体地址,通过百度地图API获取其经纬度,并存入coord列表
- for addr in address:
- loc = Html(addr).get_location()
- coordinate = str(loc).strip('()')
- coord.append(coordinate)
-
- coord_column = pd.Series(coord, name='coord')
- save = pd.DataFrame({'coord':coord_column})
- save.to_csv("coord.csv",encoding="gbk",columns=['coord'],header=True,index=False)
获取经纬度后将其整合到数据文件中,然后就可以制作基于百度地图的热力图了。注意:大量数据中难免会存在个别无法查询经纬度的地址,因此在调用百度地图API获取经纬度的模块中设置了异常处理,无法获取有效经纬度时返回0,以便后续手动查询。百度地图在浏览器中调用,需要建立一个html文件,参考官方文档:http://developer.baidu.com/map/jsdemo.htm#c1_15
注意热力图点的数据格式,需要进行转换:
- #热力图点的数据格式:var points =[{"lng":116.418261,"lat":39.921984,"count":50},...]
- #将各房屋的经纬度和价格数据按照热力图点数据格式进行转化
- coord = house['coord']
- price = house['price']
-
- for i in range(len(house)):
- lng = str(coord[i].split(', ')[0])
- lat = str(coord[i].split(', ')[1])
- count = str(price[i])
- out = '{\"lng\":'+lng+',\"lat\":'+lat+',\"count\":'+count+'},'
- print(out)
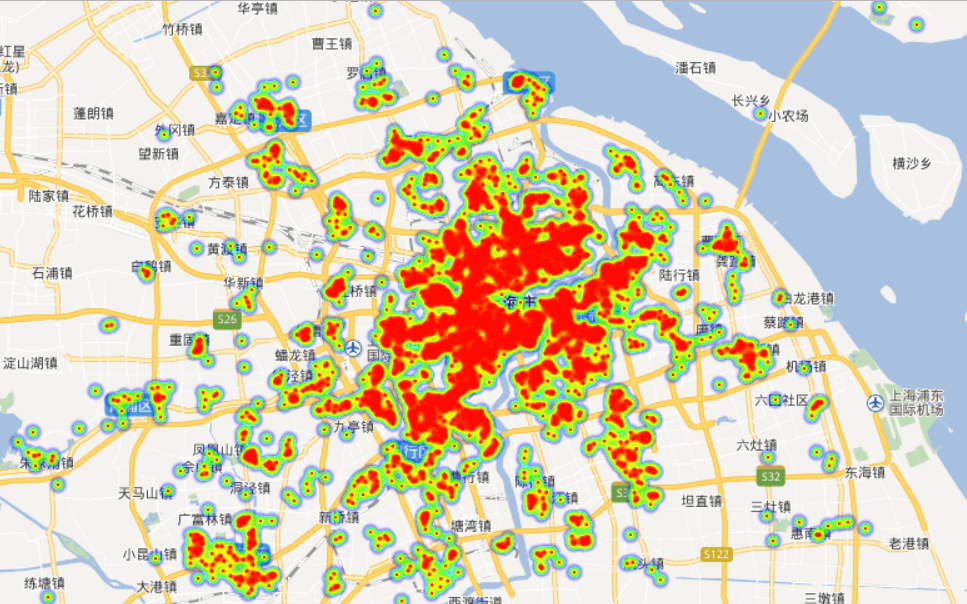
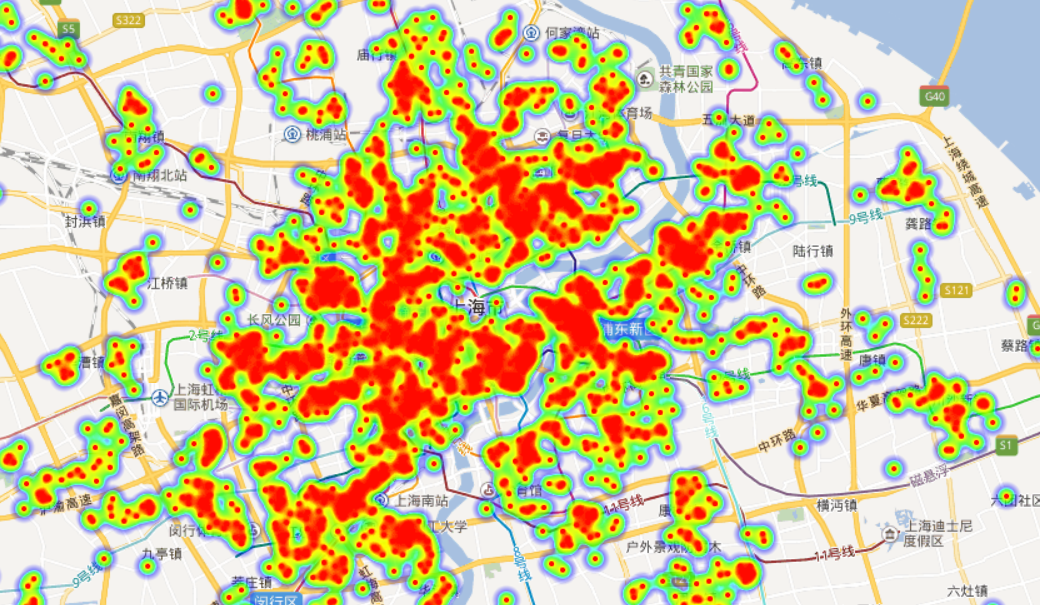
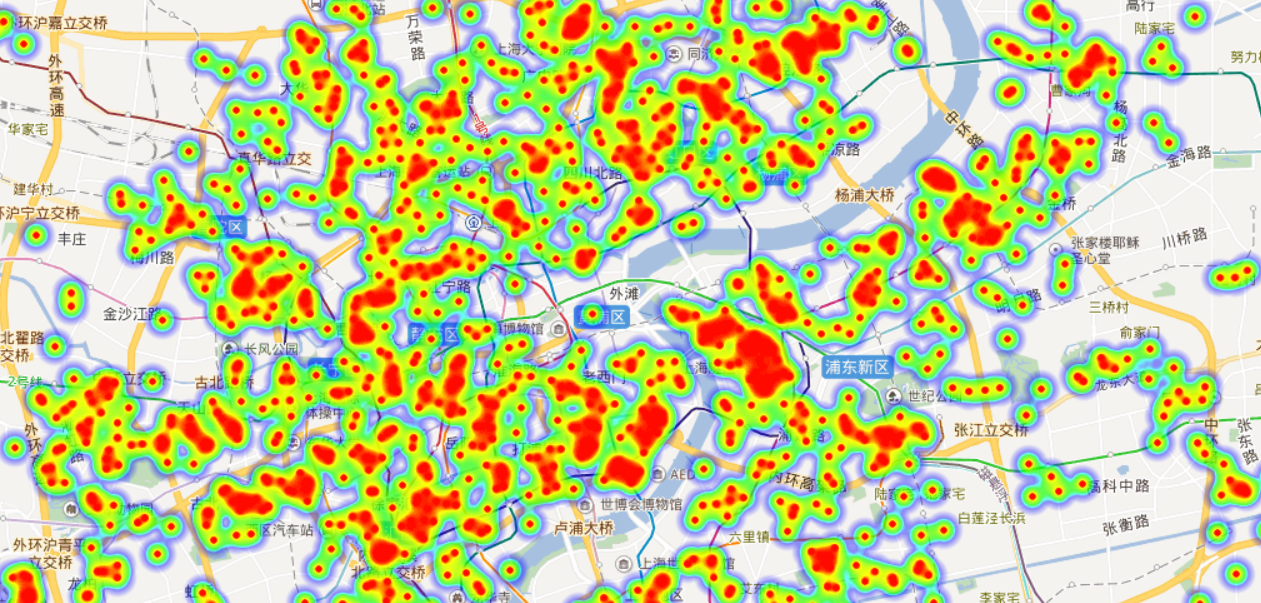
接下来比较简单,新建一个html文件,将该网页中的源代码搬运过来,并替换ak和var points中的值。需要注意的是,这里ak的应用类别必须为“浏览器端”才能在浏览器中调用百度地图。由于百度地图热力图默认以天安门为中心的北京区域地图,因此需要在BMap.Point中设置热力图的“中心点坐标”,所得热力图结果如下:
地图中热力图点的尺寸、透明度和梯度的信息可自定义设置。在浏览器中可以拖拽和缩放地图。在不同放大倍率下可以设定合适的热力图点参数,上面三幅图的放大倍率和热力图点尺寸都不一样,方便更好地展示数据。
2、关注点距离分析
仔细观察热力图点的分布,可以发现热力图点的聚集区往往存在某些关注点,如区政府、大型商场和地铁站等,这些是影响房屋分布的重要因素,同样也是影响房价的重要因素。要用具体数据分析不同关注点对附近房价的影响,可以获取这些关注点的经纬度,计算房屋与关注点的距离,并寻找房价与距离之间的关系。
在本项目中,我们分析两个距离因素对房价的影响:房屋与所在行政区划区政府的距离,以及房屋与最近地铁站之间的距离。通过百度地图API可以轻松获取地图上两点之间的真实距离,但由于百度地图API的正逆地理编码存在配额限制,方便起见这里用公式通过两个地点之间的经纬度计算距离,具体公式及其推导参考:https://blog.csdn.net/koryako/article/details/51864161
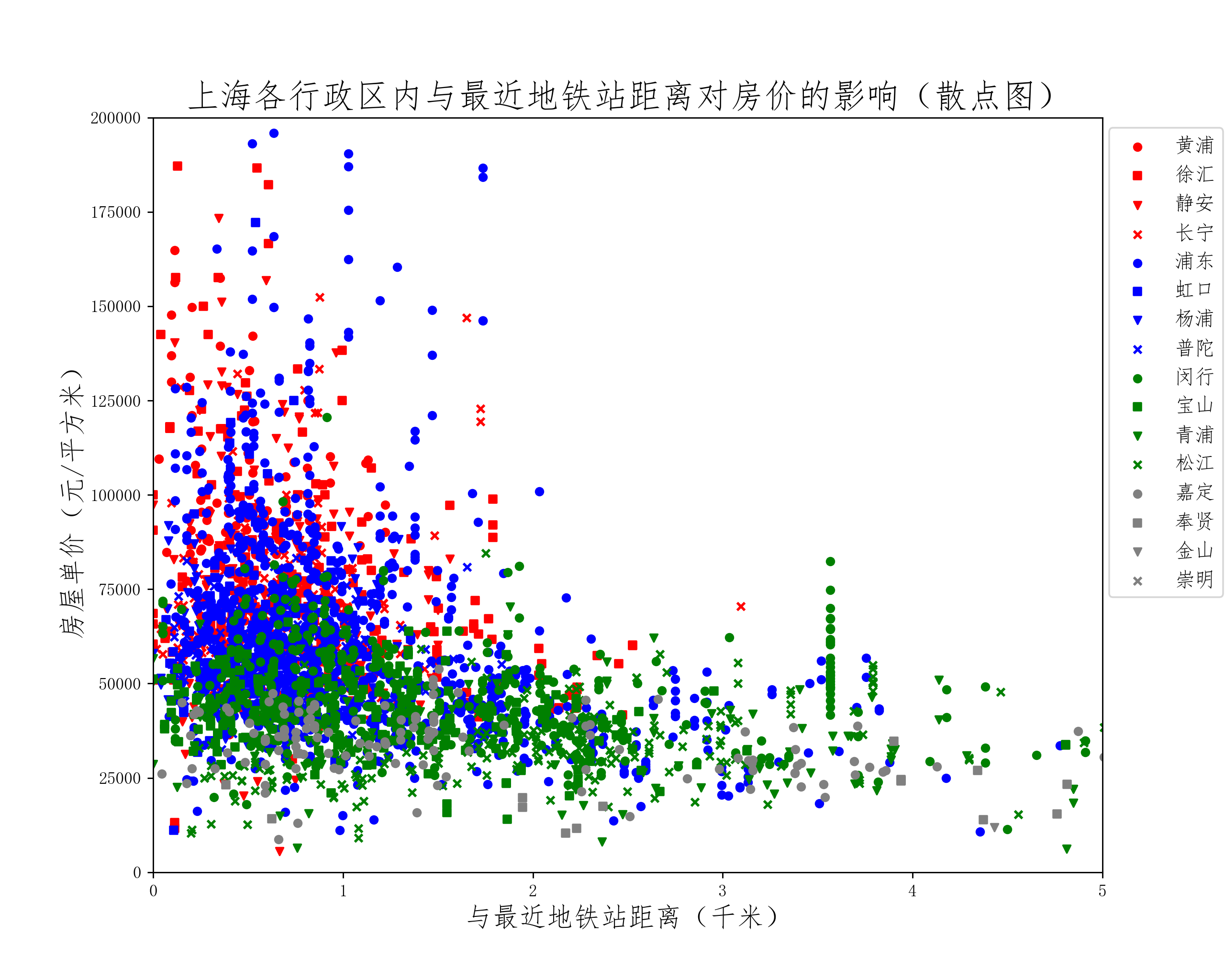
获取各房屋与所在行政区划区政府以及最近邻地铁站之间的之间距离后,分析这两个距离对房屋价格的影响,并作散点图:
从散点图的分布来看,各行政区划内与区政府及最近地铁站的距离对房价影响规律相似:随着距离增加,房价存在降低的趋势,且各区之间该趋势的程度差异较大。然而,影响房价的因素众多,从散点图上展示出来的单一因素的影响规律并不明显,需要综合考虑多个因素的共同影响。
五、机器学习预测房价
采用机器学习方法综合考虑多个因素对房价的影响,并建立预测模型。当前数据有4个特征(房屋面积、所在行政区划、与区政府及与最近地铁站之间的距离)和1个标记(房价)。因为预测目标——房价是一个连续变量,因此本项目中的价格预测是一个回归问题。
常见的机器学习回归模型有线性回归、支持向量机、K近邻、回归树和随机森林等。本项目中选取三类典型模型(线性回归、支持向量机和集成模型)进行房价预测。
1、数据预处理
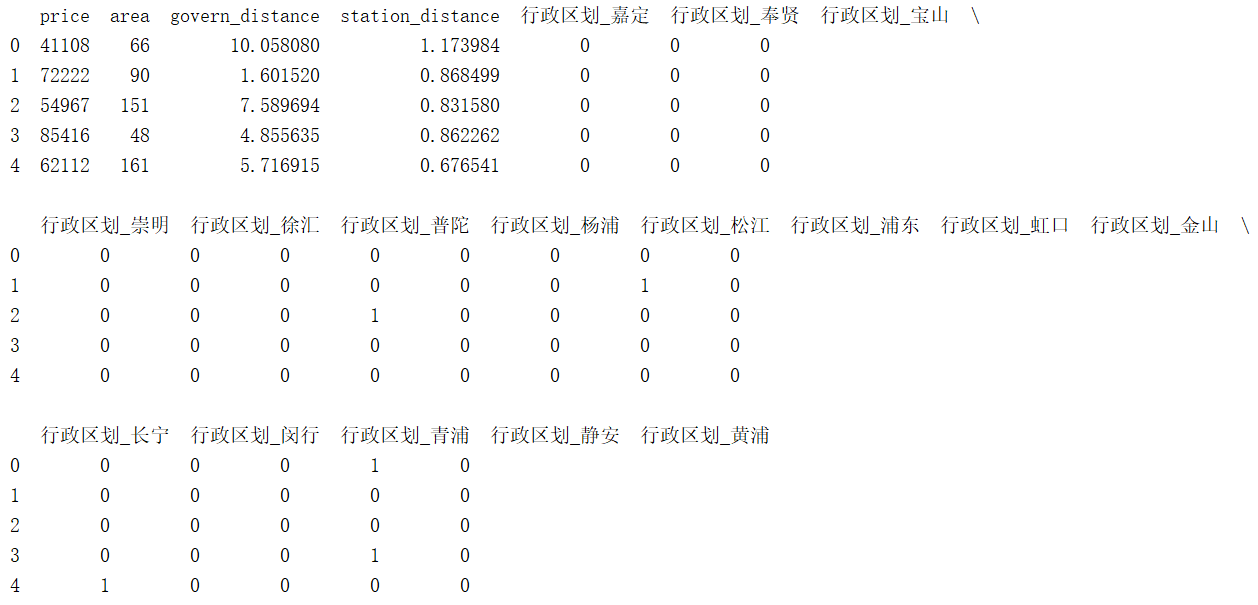
前面已经对数据进行了一系列的分析,所选的特征均对房价有明显影响,且所有数据不存在缺失现象。值得注意的是,行政区划特征为文字,这里需要使用one-hot编码,代码及结果如下:
- #使用one-hot编码修改特征"district"
- district = pd.get_dummies(house['district'], prefix='行政区划')
- data = pd.concat([house, district], axis=1)
- data.drop(['name','district','location','address','coord'], axis=1, inplace=True)
- print(data.head())
接下来,对数据进行以下处理:确定特征与标签、分割数据以及标准化处理:
- #确定数据中的特征与标签
- x = data.as_matrix()[:,1:]
- y = data.as_matrix()[:,0].reshape(-1,1)
-
- #数据分割,随机采样25%作为测试样本,其余作为训练样本
- from sklearn.model_selection import train_test_split
- x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=40, test_size=0.25)
-
- #数据标准化处理
- from sklearn.preprocessing import StandardScaler
- ss_x = StandardScaler()
- ss_y = StandardScaler()
- x_train = ss_x.fit_transform(x_train)
- x_test = ss_x.transform(x_test)
- y_train = ss_y.fit_transform(y_train)
- y_test = ss_y.transform(y_test)

2、三种机器学习回归模型预测
本项目使用线性回归、支持向量机和随机森林三种模型进行预测。由于大部分的训练模型工作sklearn库已经预置完成,只需调用模型即可,操作方法相同。这里仅展示线性回归模型(LinearRegression)的调用:
- #使用线性回归模型预测
- from sklearn.linear_model import LinearRegression
- lr = LinearRegression() #初始化
- lr.fit(x_train, y_train) #训练数据
- lr_y_predict = lr.predict(x_test) #回归预测
训练模型和预测完成后,需要对模型的预测效果进行评价。常用的评价指标有:平均绝对误差(mean_absolute_error)、均方误差(mean_squared_error)、中位数绝对误差(median_absolute_error)、解释方差得分(explained_variance_score)以及R方得分(r2_score)。虽然评价指标各有其优缺点,但没有必要全部调用。本项目中调用均方误差和R方得分两个指标,期望均方误差尽量低,R方得分尽量高。代码如下:
- #性能测评:分别使用均方误差和R方得分两个指标对模型预测结果进行评价
- from sklearn.metrics import mean_squared_error, r2_score
- print("LinearRegression模型的均方误差为:",
- mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))
- print("LinearRegression模型的R方得分为:", r2_score(y_test, lr_y_predict))
除了线性回归模型,本项目还调用了三种核函数(线性、多项式和径向基核函数)的支持向量机回归模型,以及集成模型(普通随机森林、极端随机森林和梯度提升树)对数据进行训练与预测,比较结果如下:

从表中结果可以看出,R方得分与均方误差成负相关关系,只看一个指标即可。R方得分越高,模型的预测能力越强。本项目中所用到的模型中极端随机森林模型的预测能力最强,线性回归模型的预测能力最弱。需要注意的是,通过调参和交叉验证的方法可以进一步训练模型,提高预测能力。
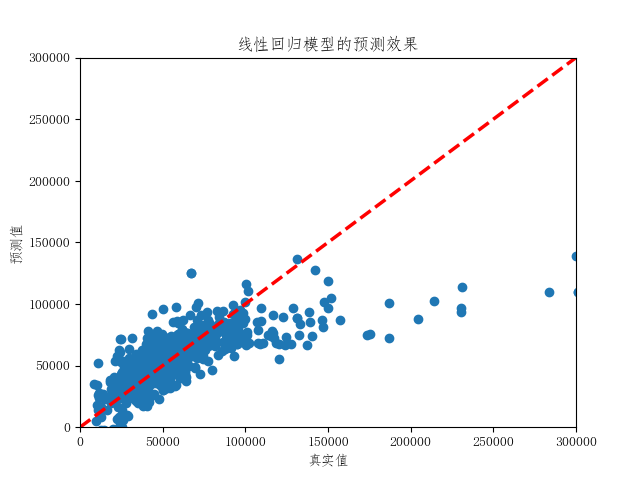
为更加直观地对比不同模型的预测能力,对模型预测结果进行可视化处理:
- #预测结果可视化
- import matplotlib.pyplot as plt
- import numpy as np
- plt.scatter(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict))
- x = np.linspace(0,300000,10000)
- plt.plot(x,x,color='red',linestyle='--',linewidth=2.5)
- plt.xlim(0,300000)
- plt.ylim(0,300000)
- plt.title('线性回归模型的预测效果')
- plt.xlabel('真实值')
- plt.ylabel('预测值')
- plt.show()
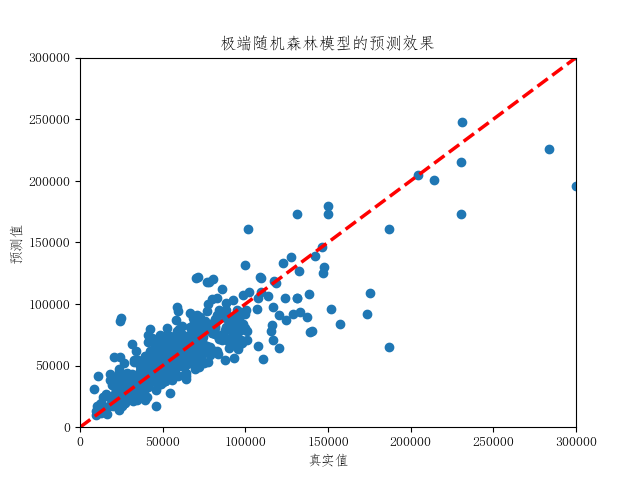
上面两幅图对比了预测效果最差的线性回归模型和预测效果最好的极端随机森林模型的预测效果。线性回归模型在低房价区间预测效果较好,但随着房价超过10万元/平方米后预测值偏低。极端随机森林模型在所有房价区间内的预测效果都很好。
六、总结
本项目收集了上海市二手房价格信息,首先采用统计分析的方法对数据进行初步分析,大致了解房价分布及其影响因素;随后调用百度地图API,编程实现数据地图可视化,并获取了具体的地址和重要的距离数据;最后采用机器学习方法建模预测,并比较了几种常用回归模型的预测效果。
本项目基本符合一个完整数据分析案例的要求,但仍有很多可以改进的地方,如可以采用更复杂的统计学理论深入分析房价分布及其影响因素,对机器学习模型进行调参以尽可能提高预测能力,采用更加直观的数据可视化方式展示数据,并通过数据分析为二手房购买者提供建设性意见。