数学与计算机（2）- 线性代数

原文：https://blog.iyatt.com/?p=13044

1 矩阵

NumPy 中 array 和 matrix 都可以用于储存矩阵，后者是前者的子类，array 可以表示任意维度，matrix 只能是二维，相当于矩阵专用，在一些矩阵的运算操作上较为直观。

1.1 创建矩阵

1.1.1 自定义矩阵

NumPy

import numpy as np

# 通过列表创建
A = [
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12]
]
array1 = np.array(A)
display(array1) # 查看矩阵
display(type(A)) # 查看列表类型
display(type(array1)) # 查看矩阵类型

# 通过元组创建
B = (
    (1, 2, 3, 4),
    (5, 6, 7, 8),
    (9, 10, 11, 12)
)
array2 = np.array(B)
display(array2) # 查看矩阵
display(type(B)) # 查看元组类型
display(type(array2)) # 查看矩阵类型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

通过元组货列表创建的矩阵类型都相同

1.1.2 随机元素矩阵

import numpy as np

array1 = np.random.random((2, 3)) # 2 行 3 列，元素范围在 0~1 de 矩阵
display(array1)

array2 = np.random.randint(1, 100, size=(3, 4)) # 3 行 4 列，元素范围在 [1,100) 的矩阵
display(array2)
1
2
3
4
5
6
7

1.1.3 特殊矩阵

1.1.3.1 零矩阵

元素全为 0 的矩阵，记作$$\mathbf O$$

NumPy

import numpy as np

a1 = np.zeros(10) # 10 个元素的零数组
print(a1.shape)

a2 = np.zeros((3, 4)) # 3 行 4 列的零矩阵
print(a2)

a3 = np.array([np.zeros(5)]) # 零向量（行向量）
print(a3)
print(a3.shape) # 查看矩阵形状
a4 = a3.reshape(5, 1) # 修改矩阵形状，改为列向量
print(a4)
print(a4.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

1.1.3.2 方阵

行列数相等都为 n 的矩阵称为 n 阶方阵，记作$$\mathbf{A_n}$$

1.1.3.3 单位矩阵

主对角线上元素全为 1，其它位置全为 0 的方阵称为单位矩阵，一般记作$$\mathbf E$$或$$\mathbf I$$

NumPy

import numpy as np

a6 = np.eye(3)
print(a6)

a7 = np.identity(4)
print(a7)
1
2
3
4
5
6
7

1.1.3.4 对角矩阵

仅在主对角线上存在非零元素，其它位置全为零的方阵称为对角矩阵。

NumPy

import numpy as np

a = (1, 2, 3)
array1 = np.diag(a) # 通过元组/列表指定对角元素创建对角矩阵
print(array1)

array2 = np.diag(array1) # 传入矩阵也可以获得对角元素（组成的数组）
print(array2)

array3 = np.array( ((1, 2, 3),(4, 5, 6),(7, 8, 9)) )
array4 = np.diag(np.diag(array3)) # 取已有矩阵的对角线创建对角矩阵
print(array4)
1
2
3
4
5
6
7
8
9
10
11
12

1.1.3.5 上三角矩阵和下三角矩阵

主对角线上非 0，主对角线下方全为 0 的是上三角矩阵，上方全为 0 的是下三角矩阵

NumPy

import numpy as np

A = np.array((
    (1, 2, 3, 4),
    (5, 6, 7, 8),
    (9, 10, 11, 12),
    (13, 14, 15, 16)
))

array1 = np.triu(A)
print(array1)

array2 = np.tril(A)
print(array2)

array3 = np.triu(A, 1) # 默认第二个参数为 0，主对角线参数会保留
print(array3)

array4 = np.tril(A, 1)
print(array4)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

1.1.3.6 对称矩阵

满足$$a_{ij}=a_{ji}$$的方阵称为对称矩阵，即元素关于主对角线对称。

1.1.3.7 同型矩阵

行列数相同的两个矩阵称为同型矩阵。

NumPy

import numpy as np

A = np.array((
    (1, 2),
    (3, 4)
))

B = np.array((
    (1, 2, 3),
    (4, 5, 6)
))

C = np.array((
    (4, 5),
    (9, 8)
))

print('A 和 B 同型：', A.shape == B.shape)
print('A 和 C 同型：', A.shape == C.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

1.1.3.8 矩阵相等

两个矩阵为同型矩阵且对应位置的各个元素相等。

NumPy

import numpy as np

A = np.array((
    (1, 2),
    (3, 4)
))

B = np.array((
    (1, 2, 3),
    (4, 5, 6)
))

C = np.array((
    (1, 2),
    (3, 4)
))

D = np.array((
    (3, 5),
    (3, 1)
))

print('A 和 B 相等：', np.array_equal(A, B))
print('A 和 C 相等：', np.array_equal(A, C))
print('A 和 D 相等：', np.array_equal(A, D))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

1.2 矩阵运算

矩阵的一些性质：https://blog.iyatt.com/?p=8284

1.2.1 矩阵加减法

同型矩阵之间才可以做加减法运算，对应位置元素相加减

NumPy

import numpy as np

A = np.array((
    (1, 2, 3),
    (5, 3, 2)
))

B = np.array((
    (1, 9, 8),
    (3, 2, 1)
))

print(A + B)
print(A - B)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

1.2.2 矩阵数乘

数$$\lambda$$与矩阵$$\mathbf A$$的乘积记作$$\lambda\mathbf A$$或$$\mathbf A\lambda$$。数乘的结果就是矩阵中的每个元素都乘以这个数。

NumPy

import numpy as np

A = np.array((
    (1, 2, 3),
    (5, 3, 2)
))

print(8 * A)
print(A * 8)
1
2
3
4
5
6
7
8
9

1.2.3 矩阵乘法

矩阵乘法要求左侧矩阵的列数等于右侧矩阵的行数，举个例子:
左一行乘右一列 = 一行一列
左一行乘右二列 = 一行二列
左二行乘右一列 = 二行一列
左二行乘右二列 = 二行二列

\begin{aligned}
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{bmatrix}
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
5 & 6
\end{bmatrix}
&=
\begin{bmatrix}
1\times1+2\times3+3\times5 & 1\times2+2\times4+3\times6 \\
4\times1+5\times3+6\times5 & 4\times2+5\times4+6\times6
\end{bmatrix}
\\
&=
\begin{bmatrix}
22 & 28 \\
49 & 64
\end{bmatrix}
\end{aligned}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

NumPy

import numpy as np

print('矩阵乘法')

A = np.array((
    (1, 2, 3),
    (4, 5, 6)
))

B = np.array((
    (1, 2),
    (3, 4),
    (5, 6)
))

print(np.dot(A, B))
print(A.dot(B))

print('-----------------------------------------')

print('一维数组乘法')
a1 = np.array( (1, 2, 3) )
a2 = np.array( (4, 5, 6) )
print(np.dot(a1, a2)) # 对应乘积之和

print('-----------------------------------------')

print('同型矩阵对应元素相乘')

C = np.array((
    (1, 2),
    (3, 4)
))

D = np.array((
    (2, 3),
    (10, 20)
))

print(C * D)
print(np.multiply(C, D))

print('-----------------------------------------')

# 一般 array 更常用
print('matrix 类型的矩阵乘法')

E = np.mat((
    (1, 2, 3),
    (4, 5, 6)
))

F = np.mat((
    (1, 2),
    (3, 4),
    (5, 6)
))

print(E.dot(F))
print(np.dot(E, F))
print(E * F)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

例 1

已知不同商店的三种水果的价格、不同人员需要水果的数量以及不同城镇不同人员的数目如表格所示。

表1 不同商店3种水果的价格

\begin{array}{}
商店水果价格 & 商店A & 商店B \\
苹果 & 8.5 & 9 \\
橘子 & 4.5 & 4 \\
梨 & 9 & 9.5
\end{array}
1
2
3
4
5
6

表2 不同人员需要的水果数量

\begin{array}{}
人员A & 5 & 10 & 3 \\
人员B & 4 & 5 & 5
\end{array}
1
2
3
4

表3 不同城镇不同人员的数目

\begin{array}{}
城镇1 & 1000 & 500 \\
城镇2 & 2000 & 1000
\end{array}
1
2
3
4

（1）计算在每个商店中每个人购买水果的费用
（2）计算每个城镇中每种水果的购买数量

NumPy

import numpy as np

A = np.array([
    [8.5, 9],
    [4.5, 4],
    [9, 9.5]
]) # 表1

B = np.array([
    [5, 10, 3],
    [4, 5, 5]
]) # 表2

C = np.array([
    [1000, 500],
    [2000, 1000]
]) # 表3

print(B.dot(A)) # 第 1 问
print(C.dot(B)) # 第 2 问
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

1.2.4 矩阵的乘方

只有方阵才能进行乘方运算。

NumPy

import numpy as np

A = np.array((
    (1, 2, 3),
    (4, 5, 6),
    (7, 8, 9)
))

B = np.mat((
    (1, 2, 3),
    (4, 5, 6),
    (7, 8, 9) 
))

print('array')
print(A**3) # 每个元素自身的 3 次方（不需要是方阵）
print(A.dot(A).dot(A)) # 三次方（矩阵乘方）

print('matrix')
print(B**3) # 三次方（矩阵乘方）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

1.2.5 转置

一个矩阵的行列互换所产生的矩阵是原矩阵的转置矩阵，矩阵$$\mathbf A$$的转置矩阵记为$$\mathbf A^T$$

NumPy

import numpy as np

print('矩阵转置')

A = np.array((
    (1, 2, 3),
    (4, 5, 6)
))

print(A)
print(A.T)
print(np.transpose(A))

print('矩阵转置创建对称矩阵')
B = np.random.randint(1, 100, size=[5, 5]) # 创建一个随机矩阵 
C = np.triu(B) # 取上三角
D = C + C.T - np.diag(np.diag(B)) # 上三角 + 转置得到的对称下三角 - 重复的主对角线
print(D)

print('验证对称矩阵')
print(np.array_equal(D, D.T)) # 对称矩阵的原矩阵和转置矩阵相等

print('行列向量转换')
E = np.array( [[1, 2, 3, 4]] ) # 向量就是一个一行或一列的矩阵
print(E)
print(E.T)
print(E.T.T)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

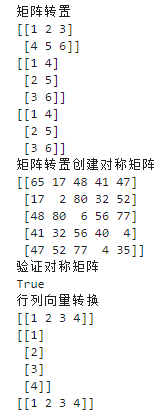
1.2.6 逆矩阵

对于n阶方阵，若存在n阶方阵$$\mathbf B$$，使得：$$\mathbf{AB}=\mathbf{BA}=\mathbf{E}$$，记作：$$\mathbf B = \mathbf A^{-1}$$，$$\mathbf A = \mathbf B^{-1}$$。一个矩阵可逆，那么逆矩阵唯一。

NumPy

import numpy as np

A = np.array([
    [1, 2],
    [2, 5]
])

B = np.mat([
    [1, 2],
    [2, 5]
])

print(np.linalg.inv(A))
print(B.I)

print('奇异矩阵 - 没有逆矩阵')
C = np.array([
    [1, -4, 0, 2],
    [-1, 2, -1, -1],
    [1, -2, 3, 5],
    [2, -6, 1, 3]
])

print(np.linalg.inv(C))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

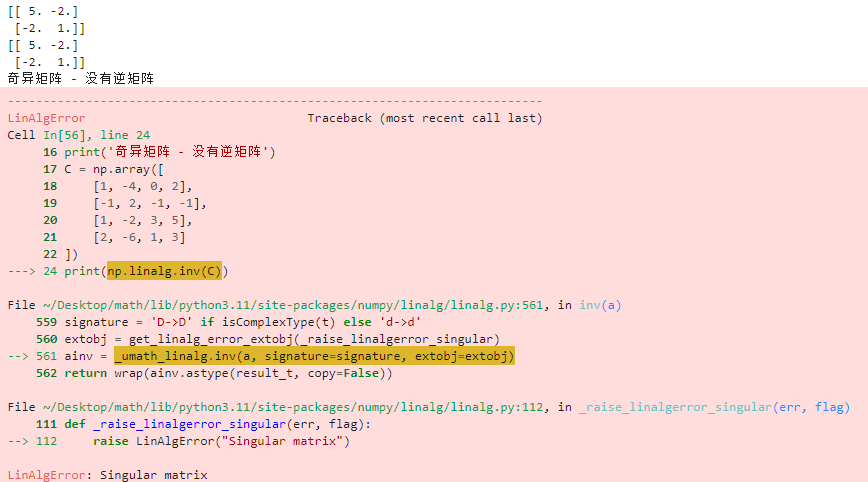
1.3 行列式

行列式主要用于判断矩阵是否可逆及计算特征方程

1.3.1 行列式值计算

验证$$|\mathbf A^{-1}|=\frac{1}{|\mathbf A|}$$
NumPy

import numpy as np

A = np.array([
    [1, 2],
    [2, 5]
])

print(1 / np.linalg.det(A))
print(
    np.linalg.det(
        np.linalg.inv(A)
    )
)
1
2
3
4
5
6
7
8
9
10
11
12
13

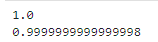
1.3.2 线性方程组求解

解方程组

\left \{
\begin{array}{l}
x+y+z=2 \\
x+2y+4z=3 \\
x+3y+9z=5
\end{array}
\right .
1
2
3
4
5
6
7

① 矩阵解线性方程组

\begin{array}{l}
\mathbf A\mathbf X=\mathbf B \\
\mathbf A^{-1}\mathbf A\mathbf X=\mathbf A^{-1}B \\
\mathbf X =\mathbf A^{-1}B
\end{array}
1
2
3
4
5

NumPy

import numpy as np

A = np.array([
    [1, 1, 1],
    [1, 2, 4],
    [1, 3, 9]
])

B = np.array([2, 3, 5])

if np.linalg.det(A) == 0:
    print('方程组无解或没有唯一解')
else:
    print(np.dot(np.linalg.inv(A),
          B))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

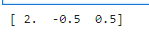
② NumPy 解线性方程组

import numpy as np

A = np.array([
    [1, 1, 1],
    [1, 2, 4],
    [1, 3, 9]
])

B = np.array([2, 3, 5]).reshape(3, 1)

print(np.linalg.solve(A, B))
1
2
3
4
5
6
7
8
9
10
11

③ SymPy 解线性方程组

import sympy as sy

sy.init_printing(use_latex=True)

x, y, z = sy.symbols('x y z')
f1 = sy.Eq(x + y + z, 2)
f2 = sy.Eq(x + 2 * y + 4 * z, 3)
f3 = sy.Eq(x + 3 * y + 9 * z, 5)

display(sy.solve((f1, f2, f3)))
1
2
3
4
5
6
7
8
9
10

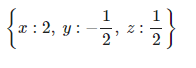
④ 克拉默法则
NumPy

import numpy as np

A = np.array([
    [1, 1, 1],
    [1, 2, 4],
    [1, 3, 9]
])

B = np.array([2, 3, 5])

A_det = np.linalg.det(A)

if A_det == 0:
    print('方程组无解或没有唯一解')
else:
    for i in range(A.shape[1]): # 列
        Ai = np.copy(A)
        Ai[:, i] = B
        Ai_det = np.linalg.det(Ai)
        print('x{} = {}'.format(i + 1, Ai_det / A_det))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

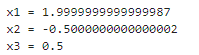
1.4 矩阵的秩

秩反映了矩阵中行（列）的最大线性无关数量。
比如

\left \{
\begin{array}{l}
2x + y = 0 \\
4x + 2y = 0
\end{array}
\right .
1
2
3
4
5
6

写成矩阵

\begin{bmatrix}
2 & 1 \\
4 & 2
\end{bmatrix}
1
2
3
4

这两个方程是成比例的，也就是线性相关，对应的矩阵秩为 1，小于未知数个数，这个方程组有无数组解。

\left \{
\begin{array}{l}
2x + y = 0 \\
4x + 3y = 0
\end{array}
\right .
1
2
3
4
5
6

写成矩阵

\begin{bmatrix}
2 & 1 \\
4 & 3
\end{bmatrix}
1
2
3
4

这个方程组中的两个方程就是线性无关的，秩为 2，等于未知数个数，有唯一确定的一组解。

NumPy

import numpy as np

E = np.eye(5)
print(np.linalg.matrix_rank(E)) # 单位矩阵的秩等于阶数

A = np.array([
    [1, -4, 0, 2],
    [-1, 2, -1, -1],
    [1, -2, 3, 5],
    [2, -6, 1, 3]
])
print(np.linalg.matrix_rank(A)) # 秩 3 < 4，行列式值为 0，前面求逆矩阵部分验证过，这个矩阵没有逆矩阵
1
2
3
4
5
6
7
8
9
10
11
12

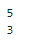
1.5 向量

1.5.1 创建向量

NumPy

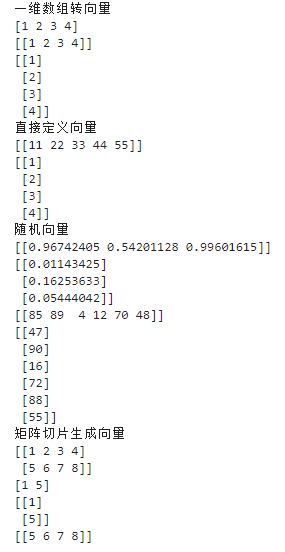
import numpy as np

print("一维数组转向量")
A = np.array([1, 2, 3, 4]) # 一维数组
print(A)
B = A.reshape(1, 4) # 行向量
print(B)
C = A.reshape(4, 1) # 列向量
print(C)

print('直接定义向量')
D = np.array([[11, 22, 33, 44, 55]])
print(D)
E = np.array([[1],[2],[3],[4]])
print(E)

print('随机向量')
F = np.random.random((1, 3))
print(F)
G = np.random.random((3, 1))
print(G)
H = np.random.randint(1, 100, size=(1, 6))
print(H)
I = np.random.randint(1, 100, size=(6, 1))
print(I)

print('矩阵切片生成向量')
J = np.array([
    [1, 2, 3, 4],
    [5, 6, 7, 8]
])
print(J)
print(J[:,0]) # 0 列数组
print(J[:,0].reshape(-1, 1)) # 第 0 列列向量
print(J[1,:].reshape(1, -1)) # 第 1 行行向量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

1.5.2 内积

$$[\mathbf x,\mathbf y]$$表示向量$$\mathbf x$$和向量$$\mathbf y$$的内积，用矩阵乘法表示$$[\mathbf x,\mathbf y]=[x_1x_2\cdots x_n]\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}$$

NumPy

import numpy as np

print('矩阵表示向量时')
A = np.array([[1, 2, 3]])
B = np.array([[4, 5, 6]])

print(A)
print(B)

print('行向量内积：', np.dot(A, B.T))

A = A.reshape(3, 1)
B = B.reshape(3, 1)

print(A)
print(B)

print('列向量内积：', np.dot(A.T, B))

print('一维数组表示向量时')

C = np.array([1, 2, 3])
D = np.array([4, 5, 6])

print(C)
print(D)

print(np.dot(C, D))
print(np.inner(C, D))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

1.5.3 长度

$$||\mathbf x||=\sqrt{[x,x]}=\sqrt{x_1^2+x_2^2+\cdots+x_n^2}$$为n维向量x的长度，当$$||\mathbf x||=1$$时，称$$\mathbf x$$为单位向量。
对于向量$$\mathbf\alpha$$，如果$$\mathbf x=\frac{\mathbf\alpha}{||\mathbf\alpha||}$$，则$$\mathbf x$$是一个单位向量，由向量$$\mathbf\alpha$$得到$$\mathbf x$$的过程称为$$\alpha$$的单位化，也称标准化。

NumPy

import numpy as np

A = np.array([[1, 2, 3]])
B = np.linalg.norm(A) # 长度
print(B)

C = A / B # 单位向量
print(C)
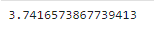
print(np.linalg.norm(C)) # 单位向量的长度
1
2
3
4
5
6
7
8
9

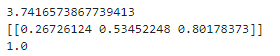
定义求长度
NumPy

import numpy as np

A = np.array([[1, 2, 3]])
print(np.sum(A**2)**0.5) # 定义求长度
1
2
3
4

1.5.4 夹角

由$$[\mathbf x,\mathbf y]=||\mathbf x||\cdot||\mathbf y||\cdot\cos\theta$$有$$\cos\theta=\frac{[\mathbf x,\mathbf y]}{||\mathbf x||\cdot||\mathbf y||}$$

NumPy

import numpy as np

A = np.array([[1, 0]])
B = np.array([[1, 3**0.5]])

cos_value = np.dot(A, B.T) / (np.linalg.norm(A) * np.linalg.norm(B)) # 余弦值
print(cos_value)
print(np.arccos(cos_value) * 180 / np.pi) # 角度
1
2
3
4
5
6
7
8

1.5.5 正交

当两个向量的内积为0时，称两个向量正交，即两个向量垂直。

1.6 NumPy 数组

1.6.1 等差 1

import numpy as np

A = np.arange(0, 10, 1) # [0,10) 之间，间隔 1
print(A)

B = np.arange(100, 1000, 200) # [100, 1000) 之间，间隔 200
print(B)
1
2
3
4
5
6
7

1.6.2 等差 2

import numpy as np

A = np.linspace(0, 10, 10) # [0,10] 之间，10 个
print(A)

B = np.linspace(10, 200, 30) # [10, 200] 之间，200 个
print(B)
1
2
3
4
5
6
7

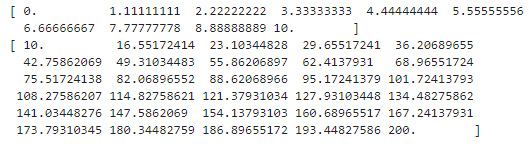
1.6.3 等比

import numpy as np

A = np.logspace(0, 3, 7) # [10^0, 10^3]，7 个
print(A)

B = np.logspace(1, 6, 5, base=2) # [2^1, 2^6], 5 个
print(B)
1
2
3
4
5
6
7

1.6.4 统计

import numpy as np

A = np.array([
    [1, 7, 3],
    [4, 5, 6]
])

print('矩阵\n', A)

print('最大值\n', A.max())
print('最小值\n', A.min())
print('每列的最大值\n', A.max(axis=0))
print('每行的最大值\n', A.max(axis=1))
print('最大值的位置\n', A.argmax()) # 从 0 开始索引
print('最小值的位置\n', A.argmin())
print('每列最大值的位置\n', A.argmax(axis=0))

print('矩阵求和\n', A.sum())
print('按行求和\n', A.sum(axis=1))

print('矩阵平均值\n', A.mean())
print('每列的平均值\n', A.mean(axis=0))

print('取中值\n', np.median(A))
print('按列取中值', np.median(A, axis=0))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

2 特征值与矩阵分解

2.1 特征值与特征向量

$$\mathbf A\mathbf x=\lambda\mathbf x$$，其中$$\mathbf x$$为向量，$$\lambda$$对应长度变化比例，称$$\lambda$$为特征值，$$\mathbf x$$为$$\lambda$$对应的特征向量。
上式整理可以得到$$(\mathbf A\mathbf x-\lambda\mathbf E)=0$$，其中$$\mathbf E$$为单位矩阵。其系数行列式$$|\mathbf A\mathbf x-\lambda\mathbf E|=0$$称为$$\mathbf A$$的特征方程，$$|\mathbf A\mathbf x-\lambda\mathbf E|$$称为$$\mathbf A$$的特征多项式。$$\mathbf x$$有非零解的充分必要条件是$$|\mathbf A\mathbf x-\lambda\mathbf E|=0$$。

例 1

求解$$\mathbf A=\begin{bmatrix}-1 & 0 & 1\\ 1 & 2 & 0\\-4 & 0 & 3\end{bmatrix}$$的特征值和特征向量。

（1）计算特征多项式$$|\mathbf A-\lambda\mathbf E|$$

\begin{aligned}
|\mathbf A-\lambda\mathbf E|&=
\begin{bmatrix}
-1-\lambda & 0 & 1 \\
1 & 2-\lambda & 0 \\
-4 & 0 & 3-\lambda
\end{bmatrix}
\\
&=(1-\lambda)^2(2-\lambda)
\end{aligned}
1
2
3
4
5
6
7
8
9
10

（2）求特征值$$\lambda$$

$$\lambda_1=2,\lambda_2=\lambda_3=1$$

（3）求各个特征值对应的特征向量

当特征值为 2 时

\begin{aligned}
\mathbf A-2\mathbf E&=
\begin{bmatrix}
-3 & 0 & 1 \\
1 & 0 & 0 \\
-4 & 0 & 1
\end{bmatrix}
\\
&\overset{r_3+4r_2}{\longrightarrow}
\begin{bmatrix}
-3 & 0 & 1 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
\\
&\overset{r_1+3r_2}{\longrightarrow}
\begin{bmatrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{bmatrix}
\\
&\overset{r_3-r_1}{\longrightarrow}
\begin{bmatrix}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\\
&\overset{r_1,r_2对调}{\longrightarrow}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{bmatrix}
\end{aligned}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

经过上面初等行变换，得到的即是

\left \{
\begin{array}{l}
x_1+0x_2+0x_3=0 \\
0x_1+0x_2+x_3=0
\end{array}
\right .
1
2
3
4
5
6

即

\left \{
\begin{array}{l}
x_1=0 \\
x_3=0
\end{array}
\right .
1
2
3
4
5
6

三个未知数，但是有效方程只有两个（秩为2），基础解系个数=3-2=1
令$$x_2=1$$，有$$\begin{pmatrix}x_1\\x_3\end{pmatrix}=\begin{pmatrix} 0\\0\end{pmatrix}$$，得基础解系$$\xi_1=\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix}0\\1\\0\end{pmatrix}$$
则$$k\xi_1(k\ne0)$$是$$\lambda_1=2$$的全部特征向量

当特征值为 1 时，

\mathbf A-2\mathbf E=
\begin{bmatrix}
-2 & 0 & 1 \\
1 & 1 & 0 \\
-4 & 0 & 2
\end{bmatrix}
\rightarrow
\begin{bmatrix}
1 & 1 & 0 \\
-2 & 0 & 1 \\
0 & 0 & 0
\end{bmatrix}
1
2
3
4
5
6
7
8
9
10
11
12

基础解系个数=3-2=1

\left \{
\begin{array}{l}
x_2=-x_1 \\
x_3=2x_1
\end{array}
\right .
1
2
3
4
5
6

令$$x_1=1$$，得基础解系$$\xi_2=\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix} 1\\-1\\2\end{pmatrix}$$

则 $$k\xi_2(k\ne0)$$是$$\lambda_2=\lambda_3=1$$的全部特征向量

NumPy

import numpy

A = np.array([
    [-1, 0, 1],
    [1, 2, 0],
    [-4, 0, 3]
])

eig_val, eig_vex = np.linalg.eig(A)
print(np.round(eig_val, 1), '\n') # 保留一位小数输出
print(np.round(eig_vex, 1))
1
2
3
4
5
6
7
8
9
10
11

第一行的是特征值，和上面计算结果一样。下面的特征矩阵是由特征（列）向量组成的，因为是标准化过的，向量平方和为 1，比如 0.4 -0.4 0.8，看比例就是 1 -1 2，和上面计算结果相符。

2.2 特征值性质

（1）对角矩阵、上三角矩阵和下三角矩阵的特征值就是它们的所有主对角线元素。
（2）若$$\lambda$$是可逆矩阵$$\mathbf A$$的特征值，则$$\lambda^{-1}$$是$$\mathbf A^{-1}$$的特征值
（3）一个方阵的特征值各不相同，则对应的特征向量都线性无关
（4）对称矩阵的特征值一定是实数，且不同特征值的特征向量两两正交

2.3 特征空间

一个特征值一旦确定，其对应的特征向量乘以任意一个标量得到的新特征向量必然也满足特征方程。因此，一个特征值对应无数个特征向量，它们的方向相同，但长度不同。
一个特征值对应的所有特征向量所组成的空间，称之为特征空间。当特征值确定，特征空间就确定了。

2.4 特征值分解

将矩阵$$\mathbf A$$分解为$$\mathbf A=\mathbf Q\sum\mathbf Q^{-1}$$ 的形式
前提$$\mathbf A$$是 n 阶方阵且可对角化
$$\mathbf Q$$ 是 $$\mathbf A$$ 的特征向量组成的矩阵，$$\sum$$ 是对角阵，其主对角线上的元素是$$\mathbf A$$的特征值。

如

\mathbf A=
\begin{bmatrix}
4 & 2 \\
1 & 5
\end{bmatrix}
=
\begin{bmatrix}
1 & -2 \\
1 & 1
\end{bmatrix}
\begin{bmatrix}
6 & 0\\
0 & 3
\end{bmatrix}
\begin{bmatrix}
\frac{1}{3} & \frac{2}{3} \\
-\frac{1}{3} & \frac{1}{3}
\end{bmatrix}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

$$\mathbf A$$的特征值分别为 6 和 3，分别对应的特征向量为$$\begin{pmatrix}1 \\ 1\end{pmatrix}$$、$$\begin{pmatrix}-2 \\ 1\end{pmatrix}$$，$$\mathbf A$$的特征向量矩阵的逆矩阵是$$\begin{bmatrix}\frac{1}{3} & \frac{2}{3} \\-\frac{1}{3} & \frac{1}{3}\end{bmatrix}$$

NumPy

import numpy as np

A = np.array([
    [4, 2],
    [1, 5]
])

eig_val, eig_vex = np.linalg.eig(A) # 特征值，特征向量矩阵
inv = np.linalg.inv(eig_vex) # 特征向量矩阵的逆矩阵

print(
    eig_vex.dot(np.diag(eig_val)).dot(inv)
)
1
2
3
4
5
6
7
8
9
10
11
12
13

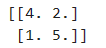
进一步，对于$$\mathbf A^n$$有$$\mathbf A^n=\mathbf Q\sum^n\mathbf Q^{-1}$$，当 n 比较大时，相比于直接计算，分解后计算量更小

2.5 奇异值分解（SVD）

前面的特征值分解只能在方阵使用 ，而 SVD 适用于对任意矩阵进行矩阵分解。

对于$$m\times n$$阶矩阵$$\mathbf A$$，$$\mathbf A^T\mathbf A$$和$$\mathbf A\mathbf A^T$$都是对称方阵，$$\mathbf A^T\mathbf A$$是 n 阶对称方阵，$$\mathbf A\mathbf A^T$$是 m 阶对称方阵，$$\mathbf{R(A^TA)=R(AA^T)=R(A)}$$，$$\mathbf A^T\mathbf A$$ 和 $$\mathbf A\mathbf A^T$$ 两个对称矩阵的非零特征值相同，剩余的零特征值个数分别为 n-r 个和 m-r 个。
对称矩阵的特征向量矩阵是正交矩阵，特征值均为实数。

SVD 公式：$$\mathbf A_{m\times n}=\mathbf U_{m\times m}\sum_{m\times n}\mathbf V_{n\times n}^T$$

\begin{array}{|l|l|l|l|l|}
\hline
矩阵 & 别称 & 维度 & 计算方式 & 含义 \\
\hline
\mathbf U & \mathbf A 的左奇异矩阵 & (m,m) & 由\mathbf A\mathbf A^T的特征向量组成，且特征向量为单位向量 & 包含了有关行的所有信息 \\
\hline
\sum & \mathbf A 的奇异值矩阵 & (m,n) & 对角元素由 \mathbf A\mathbf A^T 或 \mathbf A^T\mathbf A的特征值的平方根组成，且降序排列 & 记录 SVD 过程 \\
\hline
\mathbf V & \mathbf A 的右奇异矩阵 & (n,n) & 由\mathbf A^T\mathbf A的特征向量组成，且特征向量为单位向量 & 包含了有关列的所有信息 \\
\hline
\end{array}
1
2
3
4
5
6
7
8
9
10
11

注意$$\sum$$是特征值降序组成的，左奇异矩阵和右奇异矩阵的特征向量排序也要对应特征值。

NumPy

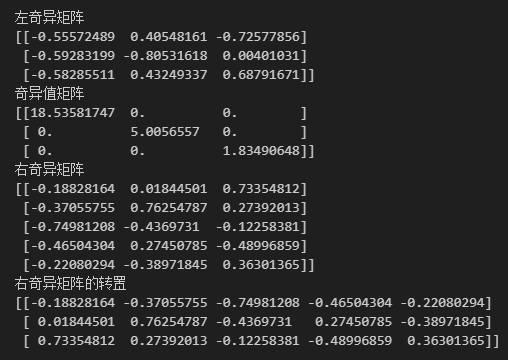
import numpy as np

A = np.array([
    [1, 5, 7, 6, 1],
    [2, 1, 10, 4, 4],
    [3, 6, 7,5, 2]
])

print('矩阵')
print(A)

U, S, VT = np.linalg.svd(A)
print('左奇异矩阵')
print(U)
print('奇异值')
print(S)
print('奇异值矩阵')
Sigma = np.zeros(A.shape)
Sigma[:len(S),:len(S)] = np.diag(S)
print(Sigma)
print('右奇异矩阵的转置')
print(VT)

print('-----------------------------------------------------------------')
print('重构矩阵')
print(
    U.dot(Sigma).dot(VT.T)
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

---

根据 SVD 公式有
$$\mathbf V^T=(\mathbf U\sum)^{-1}A=\sum^{-1}\mathbf U^{-1}\mathbf A\xlongequal{左奇异矩阵逆和转置相等}\sum^{-1}\mathbf U^T\mathbf A$$
$$\mathbf V=\mathbf A^T\mathbf U(\sum^{-1})^T=\mathbf A^T\mathbf U(\sum^T)^{-1}\xlongequal{奇异值矩阵是对称矩阵，转置等于原矩阵}\mathbf A^T\mathbf U\sum^{-1}$$
这种方式求出的右奇异矩阵可能更为紧凑，当奇异值矩阵中存在零列，那么抛掉零列再计算出来的右奇异矩阵的行数就等于奇异值矩阵中非零列的数量。

NumPy

import numpy as np

A = np.array([
    [1, 5, 7, 6, 1],
    [2, 1, 10, 4, 4],
    [3, 6, 7,5, 2]
])

# 特征值和左奇异矩阵
sigmal_val, U = np.linalg.eigh(A.dot(A.T))
# 生成特征值降序排序的索引
sigmal_sort_id = np.argsort(sigmal_val)[::-1]
# 特征值降序排序
sigmal_val = np.sort(sigmal_val)[::-1]
# 根据生成的排序索引对左奇异矩阵做对应的排序
U = U[:, sigmal_sort_id]

# 奇异值矩阵
sigmal = np.diag(np.sqrt(sigmal_val))

# 奇异值矩阵的逆矩阵
sigmal_inv = np.linalg.inv(sigmal)
# 右奇异矩阵
V_part = A.T.dot(U).dot(sigmal_inv)
# 右奇异矩阵的转置
V_part_T = V_part.T
# 或
V_part_T = sigmal_inv.dot(U.T).dot(A)

print('左奇异矩阵')
print(U)
print('奇异值矩阵')
print(sigmal)
print('右奇异矩阵')
print(V_part)
print('右奇异矩阵的转置')
print(V_part_T)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

可以看到这样计算出的奇异值矩阵少了两个零列，计算出的右奇异矩阵则少了两行。

2.5.1 SVD 矩阵近似

前面 SVD 分解结果可以看到奇异值是按降序排列的，即越是前面的数，数值越大，包含的矩阵特征就越多，那么可以在保留矩阵主要信息的情况下考虑丢掉一些后面的数据，这样可以降低数据量，得到与原矩阵近似的结果。
这里在前面示例矩阵的基础上尝试丢掉一些奇异值，再计算还原矩阵。

NumPy

for k in range(3, 0, -1):
    print('k=', k)
    D = U[:,:k].dot(Sigma[:k,:k]).dot(VT[:k,:]) # U 的前 k 列，Sigma 的前 k 行 k 列，VT 的前 k 行
    print(np.round(D, 1)) # 保留一位小数，方便观察
1
2
3
4

2.5.2 例 1 使用 SVD 压缩图像

根据前面 SVD 矩阵近似的原理，尝试对图像丢掉一定比例的奇异值，比较对还原的最终图像的影响。
奇异值比例控制，这里有两种思路，一种是按奇异值数据和的比例，比如奇异值有 5、4、3、2、1，总和是 15，假如保留 60%，也就是只要前 $$15\times60\%=9$$，即5、4，再后面的奇异值就丢弃了。另外一种思路是按奇异值个数，60% 就是数个数，共 5 个，前 60% 就是前 3 个，即 5、4、3。下面的代码就是这两种思路的实现。

import numpy as np
import matplotlib.pyplot as plt

def get_approx_SVD(data, percent, type):
    U, s, VT = np.linalg.svd(data)
    Sigma = np.zeros(np.shape(data), dtype=data.dtype)
    Sigma[:len(s), :len(s)] = np.diag(s)

    if type == 1:
        total_sum = int(sum(s) * percent)
        k = -1
        current_sum = 0
        while current_sum <= total_sum:
            k += 1
            current_sum += s[k]
    elif type == 2:
        k = int(len(s) * percent)

    D = U[:, :k].dot(Sigma[:k, :k].dot(VT[:k, :]))
    return D.astype(data.dtype)

def rebuild_img(img, percent, type):
    R0 = img[:, :, 0] # 分离 RGB 颜色通道
    G0 = img[:, :, 1]
    B0 = img[:, :, 2]
    R = get_approx_SVD(R0, percent, type)
    G = get_approx_SVD(G0, percent, type)
    B = get_approx_SVD(B0, percent, type)
    return np.stack((R, G, B), 2)


img_path = 'test.png' # 图片路径
img = plt.imread(img_path)

images1 = []
images2 = []
current_percent = 0
for i in range(10):
    current_percent += 0.1
    images1.append(rebuild_img(img, current_percent, 1))
    images2.append(rebuild_img(img, current_percent, 2))

rows = 4
cols = 5
fig, axis = plt.subplots(rows, cols)
fig.subplots_adjust(left=0, right=1, bottom=0, top=1)

for i, ax in enumerate(axis.flat):
    if i < len(images1):
        ax.imshow(images1[i])
    elif i - 10 < len(images2):
        ax.imshow(images2[i - 10])
    ax.axis('off')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

前面 10 张图是奇异值和的百分比从 10% 到 100%，后面 10 张图是按奇异值个数的百分比。在我使用的图片中，按照奇异值和的比例可以很好地呈现出变化，而按个数则不是那么明显。说明这张图片较大的奇异值与较小的奇异值差距非常明显，且较大的奇异值非常的集中，在总个数中占比非常小，所以按奇异值个数的百分比看不出明显变化，而按奇异值的和的比例非常明显。一般来说，按照奇异值和的比例比较靠谱，奇异值个数比例不确定性很大（看奇异值大小分布）。