计算机系统基础 第二章_计算机系统基础逻辑运算

数值与编码

二进制编码

表示一个数值需要三个要素：

1. 进位计数制
2. 定/浮点数表示
3. 编码规则

进位计数制

在R进制数字系统中，采用R个符号（0,1,2…R-1）表示各位上的数字
采取逢R进一的运算规则，对每一个数位i，权为Rⁱ,R被称为该数字系统的基
后缀字母：

• B：二进制
• O：八进制
• D：十进制
• H：十六进制，也可用0x前缀

进制转换：十进制转成R进制
整数部分：除基取余，上左下右
小数部分：乘基取整，上左下右

定点和浮点表示

定点数：小数点约定在固定位置的数
浮点数：小数点位置约定为可浮动的数
定点表示：对定点小数和定点整数进行表示
对于定点小数小数点总是固定在数的左边，一边用来表示浮点数的尾数
对于定点整数小数点总是固定在数的右边，一般用来表示整数
浮点表示：由S（符号）E（阶码——二进制定点整数）M（尾数——二进制定点小数）组成
X = （-1)^S * M * R^E
在R一定的情况下，M的位数反映X的有效位数，决定了数的表示精度，E的位数决定了X的表示范围，确定了小数点的位置

定点数的编码表示:

1. 原码表示法：符号位直接跟数值位
2. 补码表示法：正数的补码符号为0，数值部分是它本身，负数的补码等于模与负数绝对值的之差
   当X为正数时，[X]_补=M+X（mod M）
   当X为负数时，[X]_补=M-|X| (mod M)
   [X]_补 = 2ⁿ+X(真值
   可由原码各位取反，末位加1得到补码
   [-2^n-1]_补 = 100……0
   [-1]_补 = 111……1
   [0]_补 = 000……0
3. 反码表示法：原码各位取反，反码0的表示不唯一
4. 移码表示法:用来表示阶码，对每个阶都加上一个正的常数，称为偏执常数，这使所有阶码都转成正整数，阶E的移码的位数为n，[E]_移=偏置常数+E，通常偏执常数取2^n-1或2^n-1-1

整数的表示

C中的整数及其相互转换

允许有符号数和无符号数之间的转换
若同时用带符号数和无符号数，常常将带符号数转换成无符号数

浮点数的表示

表示范围

正数范围：
最大值：0.11……1*2^11……1=（1-2^-24）2¹²⁷
最小值：0.10……02^00……0=（1/2）*2^-128
负数范围：
与正数关于原点对称
不能用浮点数表示的区间称为溢出区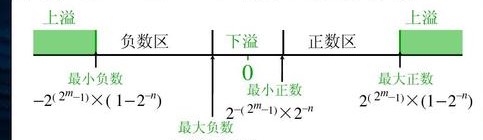

规格化

为了得到更多的有效数字，对浮点数的尾数进行规格化，同时规定规格化数的小数点前为1
规格化操作分为左规和右规
当有效数位进到小数点前面，需要右规，此时阶码可能溢出
当尾数出现0.0……0bbbbb这种结果时，需要进行左规

IEEE 754浮点数标准

32位和64位浮点数格式分别为1 8 23和1 11 52
此时移码取2^n-1-1，所以偏置常数分别为127和1023

C中的浮点数类型

当发生强制类型转换时
int转成float时：不会发生溢出但有效数字可能会被舍去
int或float转换成double时：更加精确
double转换成float时：可能溢出
当float或double转换成int时，因为int没有小数部分所以数据可能会向0方向被截断

十进制数的表示

用ASCII码表示

0-9对应30H-39H
A-Z对应41H-5AH
a-z对应61H-7AH

用BCD码表示

1. 有权BCD码
   每个二进制数位都有一个确定的权比如8421码
2. 无权BCD码
   用的较多的是余3码和格雷码

非数值数据的编码表示

逻辑值

运算按位进行，靠指令的操作码类型来识别

西文字符

使用最广泛的是ASCII码

汉字字符

输入码（外码）：使每一个汉字用一个或几个键来表示，这种对每个汉字用对应的按键进行的编码表示就称为输入码
国际码（又称国际交换码）选出了6763个常用汉字
区位码：用字符所在的区号及位号的二进制代码表示，7位区号在左，7位位号在右，这14位代码位汉字的区位码，区位码指出了汉字在码表的位置，区号和位号各自加上32（20H）为国际码
机内码：将国际码的两个字节的第一位置1，就为机内码

数据的宽度和存储

宽度和单位

二进制数据的每一位（0/1）是组成二进制信息的最小单位称为比特（bit），或称为位元，简称位
kb = 1000b
每个西文字符需要用8个bit表示，每个汉字需要用16个bit表示
二进制信息的计量单位是字节（byte），也称为位组 kb = 1024b
1byte = 8bits
存储器按照字节编址，字节是最小的可寻址单位
字：被处理信息的单位，用来度量数据类型的宽度，字和字长宽度可以相同也可以不同
字长：CPU内部用于整数运算的数据通路的宽度

存储和排列顺序

一般用最低有效位（LSB）和最高有效位（MSB）表示最高位和最低位

排列顺序：

• 大端方式：最高有效字节存储在小地址单元中，最低有效字节存放在大地址单元中（从上到下递增）
• 小段方式：和大端方式相反

数据的基本运算

按位运算和逻辑运算

按位运算：
对位串实现掩码操作或相应的其他处理（主要用于多媒体数据或状态/控制信息进行处理）
从y提取低位字节病逝高位字节为0可用&实现掩码操作
逻辑运算：
是非数值运算，用非0数表示逻辑值True，全0为False

左移运算和右移运算

移位运算目的：

1. 提取部分信息
2. 扩大或者缩小2倍

左移：高位溢出 低位补0
右移：高位补符号，低位溢出

逻辑移位：无符号数
左移高位移出，低位补0，可能溢出
右移地位移出，高位补0，可能溢出
算术移位：带符号数
左移：高位移出，低位补0，可能溢出（若移出的位不等于新的符号位则溢出）
右移：低位移出，高位补符，可能有效数字丢失

位扩展运算和位截断运算

位扩展方式：

1. 0扩展：无符号数（前面补0） 指针，地址通常是无符号整数
2. 符号扩展：有符号数（前面补符）

位截断：发生在将长数转换成短数时，可能会因为溢出改变它的值

整数加减运算

sub = 1 减法
sub = 0 加法
ZF:零标志 若X与Y’同号但与sum不同号时为1，否则为0
SF:符号标志 sum符号
OF:溢出标志 sum = 0则为1，否则为0
CF:进/借位标志 cout 异或 sub

溢出条件：
无符号：CF=1（进位）
带符号：OF=1

做减法比较大小：
无符号：CF=0 则大于
带符号：OF=SF则大于

无符号数：
加法：

• 当x+y<2ⁿ,result=x+y
• 当2ⁿ<=x+y<2ⁿ⁺¹,result=x+y-2ⁿ

减法：

• 当x-y<0 ,result=x-y+2ⁿ
• 当x-y>=0,result = x-y

有符号数：
减法：

• 当x-y<-2^n-1,result=x-y+2ⁿ
• 当-2^n-1<=x-y<2^n-1,result=x-y
• 当x-y>=2^n-1,result=x-y-2ⁿ

加法：

• 当x+y<-2^n-1,result=x+y+2ⁿ
• 当-2^n-1<=x+y<2^n-1,result=x+y
• 当x+y>=2^n-1,result=x+y-2ⁿ