逻辑回归原理以及代码实现 基于numpy_逻辑回归原理及代码实现

---

一、逻辑回归原理

逻辑回归是一种基于回归思想来解决分类问题的一个算法，利用线性回归输出的值，进行一定的处理转化为分类的标签值

分类问题和回归问题的区别

我们可以按照任务的种类,将任务分为回归任务和分类任务。分类问题的输出是离散值，例如识别猫狗，任务的输出只能是猫或者狗，是离散值。回归问题的输出是连续值，例如根据某些特征预测一个人的体重，体重是连续值。

考虑：线性模型的输出值为连续值，如何将它与分类问题联系起来？

找⼀个单调可微函数将分类任务的真实标记 y 与线性回归模型的预测值联系起来
z=$\theta$T x + b的输出是实值，我们将实值z转化为0/1值，使用对数几率函数。

对数几率函数（sigmoid函数）

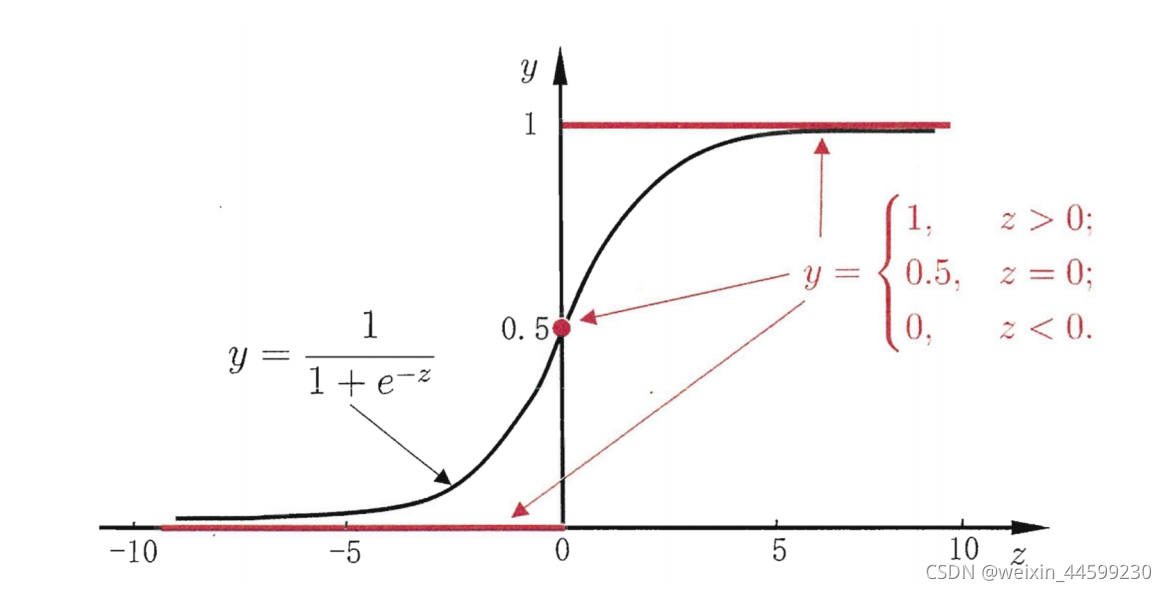
其中z=$\theta$T x + b 是线性回归的输出。
x和$\theta$是同纬度的向量，x有几个特征$\theta$就有几个分量
sigmoid函数的输出值大于0.5就判断为正类，小于0.5就判断为负类

代价函数

当y=1时 输出h越接近1 代价越小，越远离1代价越大，当y=0时，输出h越接近0代价越小，越远离0代价越大

由于还需判断y的值，则将此式子合并成为一个式子

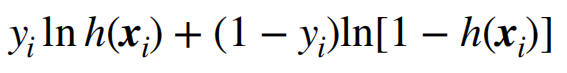
参数更新方法：梯度下降法

对于某个参数$\theta$，算出损失对这个参数的偏导数g，则更新$\theta$=$\theta$-α*g，α是学习率，手动设置的超参数。设置过大导致模型无法收敛，设置过小则导致收敛过慢，所以需要设置合适的大小。

sigmoid函数的导数推导

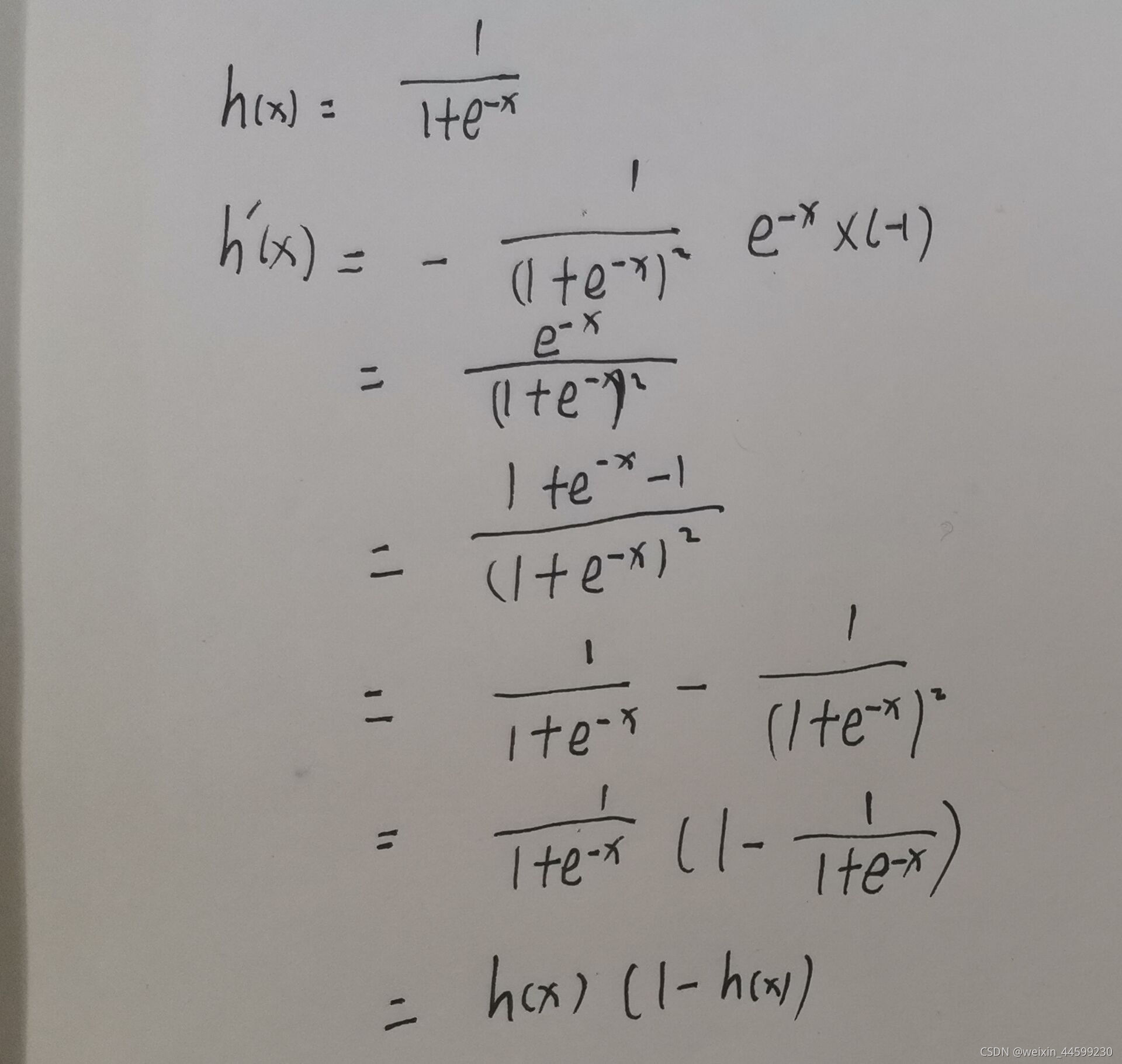
代价loss对参数求导推导过程
为了计算方便，将在x第一个位置添加一个分量1，与$\theta$相乘后分量1的位置代表偏置值，因此$\theta$也许多出一个分量，之前的z=$\theta$Tx+b，变成了z=$\theta$Tx，少了一个偏置值b，但x和$\theta$分别多加了一个分量，相乘可代表偏置值b。

二、代码实现

from sklearn import datasets
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import  StandardScaler

def sigmoid(x):
    #添加判断防止e的正数次幂过大导致溢出
    if x>0:
        return 1/(1+np.exp(-x))
    else:
        return np.exp(x)/(1+np.exp(x))
#h(x)函数
def fun_h(thetas,x):
    z=np.dot(thetas,x)
    h=sigmoid(z)
    return h

class model():
    def __init__(self,num_iters=20,lr=0.1):
        """
        :param num_iters: 迭代次数
        :param lr: 学习率
        """
        self.num_iters=num_iters
        self.lr=lr
    def fit(self,X,Y):
        """
        :param X: 训练集特征数据
        :param Y: 标签
        :return:
        """
        #初始化参数θ
        self.thetas = np.zeros(X.shape[1])
        m = len(X)
        for k in range(self.num_iters):
            for j in range(len(self.thetas)):
                d_thetaj = 0
                loss = 0
                for i in range(m):
                    h = fun_h(self.thetas, x_train[i])
                    loss += -(Y[i] * np.log(fun_h(self.thetas, x_train[i])) + (1 - Y[i]) * np.log(1 - fun_h(self.thetas, x_train[i])))
                    d_thetaj += (h - Y[i]) * x_train[i][j]
                loss /= m
                d_thetaj /= m
                self.thetas[j] -= self.lr * d_thetaj

            print("iter:%d,loss:%f"%(k,loss))
    #判断类别
    def predict(self,x):
        h=fun_h(self.thetas,x)
        if h>=0.5:
            return 1
        else:
            return 0
    #计算测试集准确率
    def score(self,x_test,y_test):
        num_correct = 0
        for x, y in zip(x_test, y_test):
            y_hat = self.predict( x)

            if y_hat == y:
                num_correct += 1
        return num_correct / len(x_test)
if __name__ == '__main__':
    cancer = datasets.load_breast_cancer()

    data=cancer.data
    target=cancer.target

    #进行数据标准化
    std = StandardScaler()
    data = std.fit_transform(data)

    #对数据添加一列1方便计算
    ones=np.ones((len(data),1))
    data=np.c_[ones,data]

    x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2, random_state=0)

    model=model(30,0.1)
    model.fit(x_train,y_train)
    score=model.score(x_test,y_test)
    print("acc:",score)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

运行结果：
iter:0,loss:0.545435
iter:1,loss:0.458332
iter:2,loss:0.401712
iter:3,loss:0.361705
iter:4,loss:0.331730
iter:5,loss:0.308293
iter:6,loss:0.289367
iter:7,loss:0.273695
iter:8,loss:0.260458
iter:9,loss:0.249093
iter:10,loss:0.239204
iter:11,loss:0.230502
iter:12,loss:0.222772
iter:13,loss:0.215849
iter:14,loss:0.209604
iter:15,loss:0.203937
iter:16,loss:0.198765
iter:17,loss:0.194023
iter:18,loss:0.189656
iter:19,loss:0.185618
iter:20,loss:0.181872
iter:21,loss:0.178386
iter:22,loss:0.175131
iter:23,loss:0.172085
iter:24,loss:0.169227
iter:25,loss:0.166539
iter:26,loss:0.164005
iter:27,loss:0.161612
iter:28,loss:0.159348
iter:29,loss:0.157202
acc: 0.956140350877193

Process finished with exit code 0

loss在逐步下降，最终测试集也达到了不错的正确率95％

总结

提示：这里对文章进行总结：
以上就是今天要讲的内容，本文仅仅简单介绍了逻辑回归简单原理，以及numpy实现基于sklearn乳腺癌数据集