- 1python数据分析综合案列--星巴克门店数据分析及可视化_python星巴克数据分析
- 2Android之Fragment应用——一个简易版的新闻应用_fragment的最佳实践:一个简易版的新闻应用
- 3打破工作“二八法则” UniPro用AI提升工作效率_研发二八定律
- 4Elasticsearch--配置说明_elasticsearch.yml本地如何配置
- 5AI运动:阿里体育端智能最佳实践_运动ai测评
- 6Java程序员如何提升自我?可以从这8方面出发_除了工作外怎么提升java基数
- 7transformers重要组件(模型与分词器)_transformers 分词器
- 8SentencePiece python 实战_sentencepiecetrainer.train
- 95.3.1 配置交换机 SSH 管理和端口安全
- 10调用ChatGPT API_调用chatgpt的api
你不一定了解MySQL中的Decimal数据类型_mysql decimal
赞
踩
一、前言
在此之前笔者写过一篇博客《你说精通MySQL其实很菜jī(基础篇):你不一定会的基本技巧或知识点(值得一看)》,本文内容是从那篇博客截取出来的。MySQL中Decimal数据类型大家经常使用到,但是,你真的了解这种数据类型吗?笔者按照官方文档探索了一番,能力有限,不一定做到完全无错误,希望广大读者能及时指出问题,大家一起学习和进步。
与MySQL相关的安装部署博客如下:
最新MySQL-5.7.40在云服务器Centos7.9安装部署
写最好的Docker安装最新版MySQL8(mysql-8.0.31)教程(参考Docker Hub和MySQL官方文档)
本文由 CSDN@大白有点菜 原创,如需转载,请说明出处。如果觉得文章还不错,可以 点赞+收藏+关注 ,你们的肯定是我创作优质博客的最大的动力。
二、什么是Decimal
Decimal属于定点类型(Fixed-Point Types),是 NUMERIC 的实现。和浮点数(Double和Float,近似值)不同,它是一种精确值,用于存储精确的数字数据值,例如货币数据。MySQL 以二进制格式存储 Decimal 值。那你们知道Decimal最大支持多少位吗?参数值如何写呀?占用多大空间呀?
Decimal类型主要关注两个重要参数:精度(precision)和小数位数(scale)。官方在 Decimal数据类型特征 文档中有详细介绍,包括最大位数、存储格式、存储要求几大主题。笔者对比过,MySQL8.0和5.7的文档介绍内容是一样的,笔者选取8.0的文档来介绍。
Decimal 默认最大位数(精度,precision)是 10 ,默认小数点位数(scale)是 0 。最大位数(精度,precision) M 范围为 1 到 65 ,小数点位数(scale) D 范围为 0 到 30 ,整数位数为(M - D),小数点位数为 D 。Decimal 使用 二进制格式存储。
DECIMAL(M,D)
- 1
例如 DECIMAL(5,2),精度是 5 ,小数位数是 2 ,整数位数是 5 - 2 = 3 ,是怎么在数据库中体现出来的呢?如果精度太小,是会报超出范围错误的。我们先来看看过程操作,那样能更好地理解 DECIMAL 的具体用法。
【MySQL官方8.0、5.7关于Decimal介绍的文档地址,并附上划词翻译插件的谷歌翻译】:
https://dev.mysql.com/doc/refman/8.0/en/fixed-point-types.html
https://dev.mysql.com/doc/refman/5.7/en/fixed-point-types.html
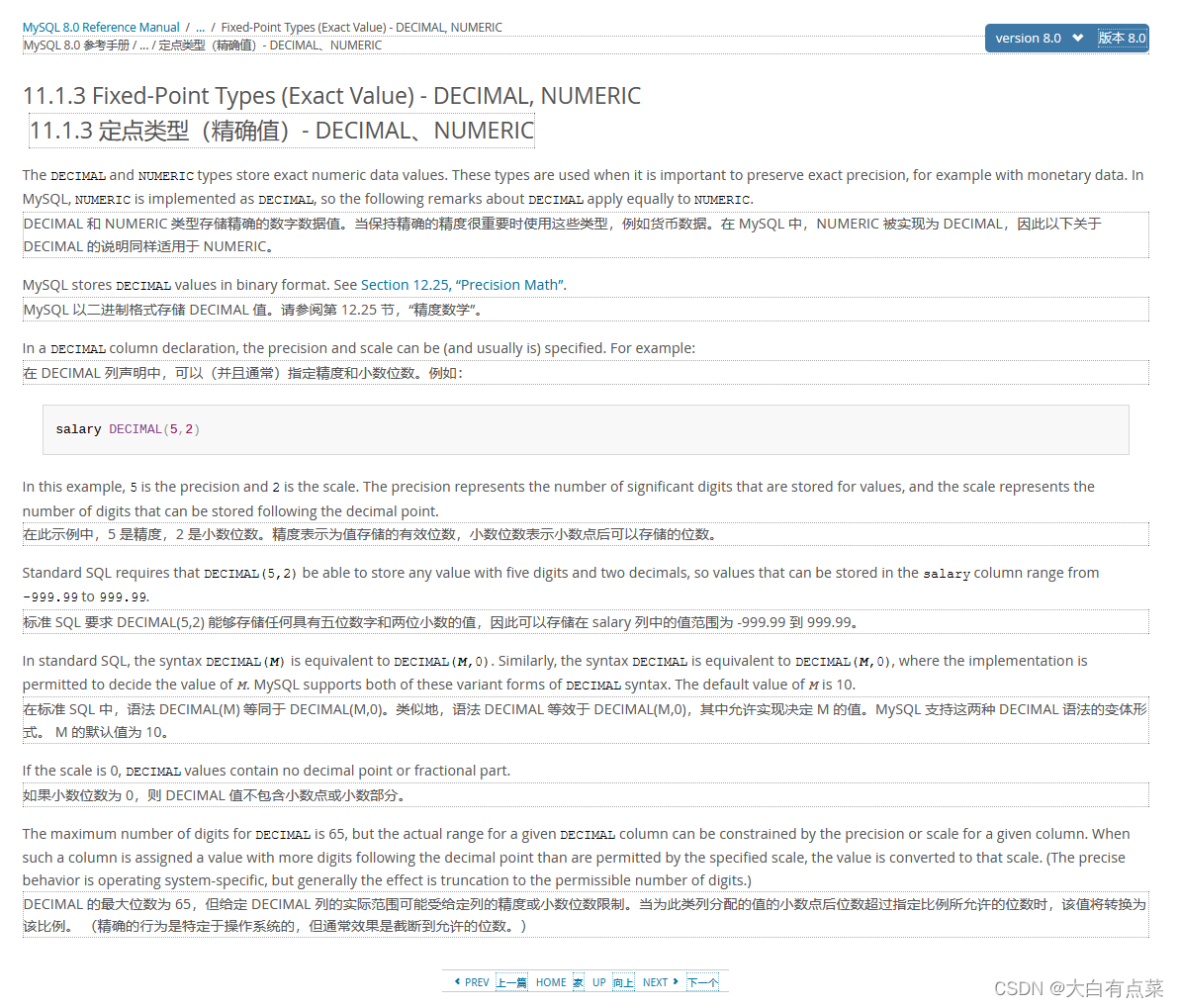
笔者使用第三方可视化工具 Navicat 新建的 tb_user 表中有一个 money 字段,数据类型设置为 decimal ,“长度” 和 “小数点” 都不设置数值,保存后,自动默认赋值,“长度”赋值为 10 ,“小数点”赋值为 0 。同时 money 字段的数值显示是没有小数部分的。
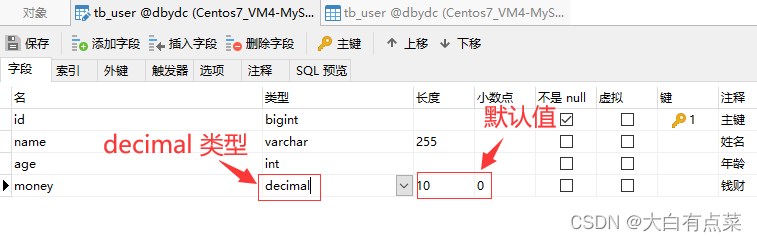
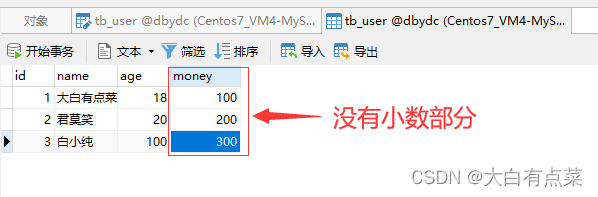
如果将“小数点”设置为 2 ,那么 money 字段的数值显示出现了小数点,并且全是 0。
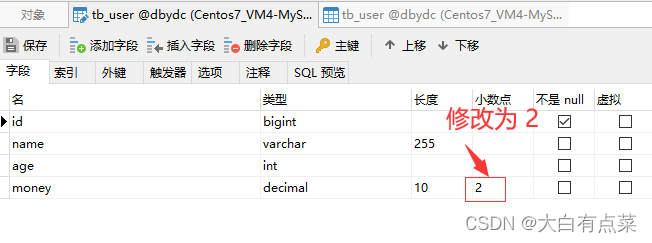
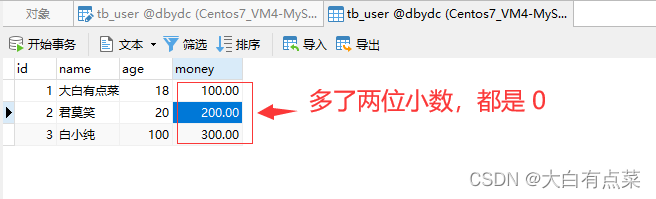
笔者将 money 字段的数值修改为具体的小数,同时将“长度”修改为 5 ,“小数点”修改为 2 ,保存是成功的,并不报错。此时数值的长度一共有5个,包括整数部分3个和小数部分2个,例如 200.02 。
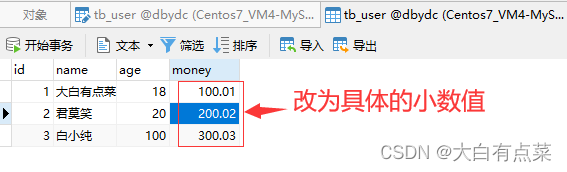
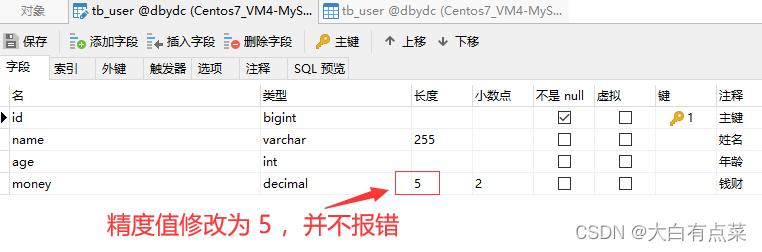
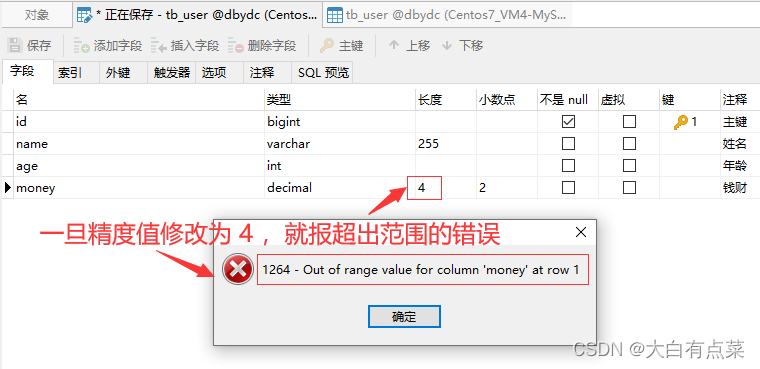
一旦将“长度”修改为 4 ,“小数点”保持 2 不变,再次保存时,立马报错:1264 - Out of range value for column 'money' at row 1 大概意思就是 money 列的值超出范围。这个报错也很容易找到原因,因为前面存储的数值(如200.02)是5位精度的,现在修改为4位精度,肯定会超出范围错误啦!
【定点类型(Fixed-Point Types)总结】
1、如果存储的数值要求精度(长度)特别大,默认值 10 是远远不够用的,不然会报超出值范围异常。不要遗漏设置小数点位数。
2、如果存储的数值要求准确的精度,千万不要使用浮点数(double 或 float)类型,一定要选择定点数(小数)类型(decimal),因为浮点数是近似值,小数才是精确值。有符号整数值不超过 127 ,无符号整数值不超过 255 的建议使用tinyint类型,那样占用空间更小。
3、一定要注意注意再注意,如果小数点位数从 2 设置到 0,再从 0 设置回 2 ,那是会导致具体的小数部分丢失的,即200.02 -> 200 -> 200.00,也就是最后不会变回 200.02 ,而是直接丢失了小数 0.02 那部分而变成了 200.00。
【延伸阅读】
官方文档关于 DECIMAL 数据类型特征介绍:
https://dev.mysql.com/doc/refman/8.0/en/precision-math-decimal-characteristics.html
笔者在查阅相关资料的时候,看到有些博文写到 decimal 的占用字节是如何算出来的,然后笔者也去MySQL官网查询,发现根本不是写的那么一回事?难道别人写的是错误的?现在就来分析一下,看看网上的博客写的有关 decimal 占用字节和官网介绍的有哪些出入。
先贴一部分网上博客的内容截图,如下所示:
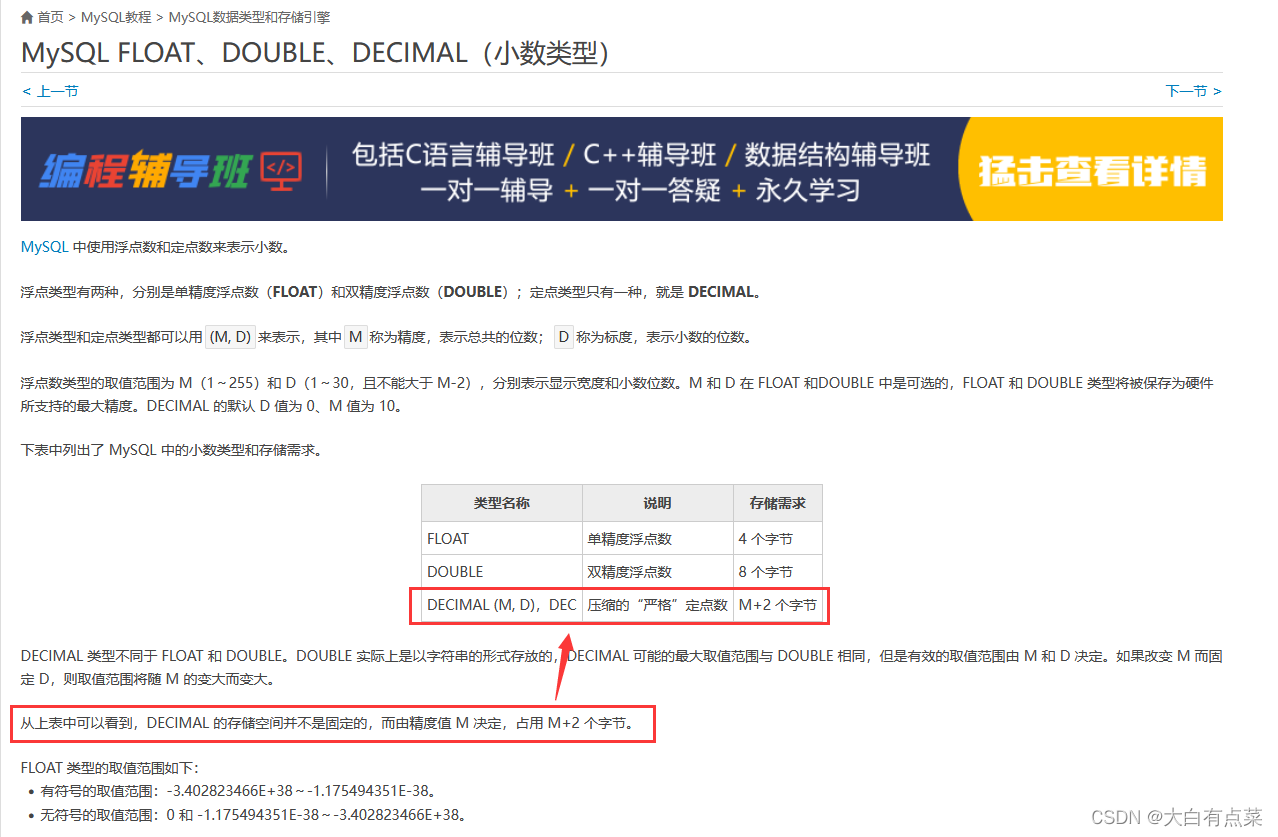
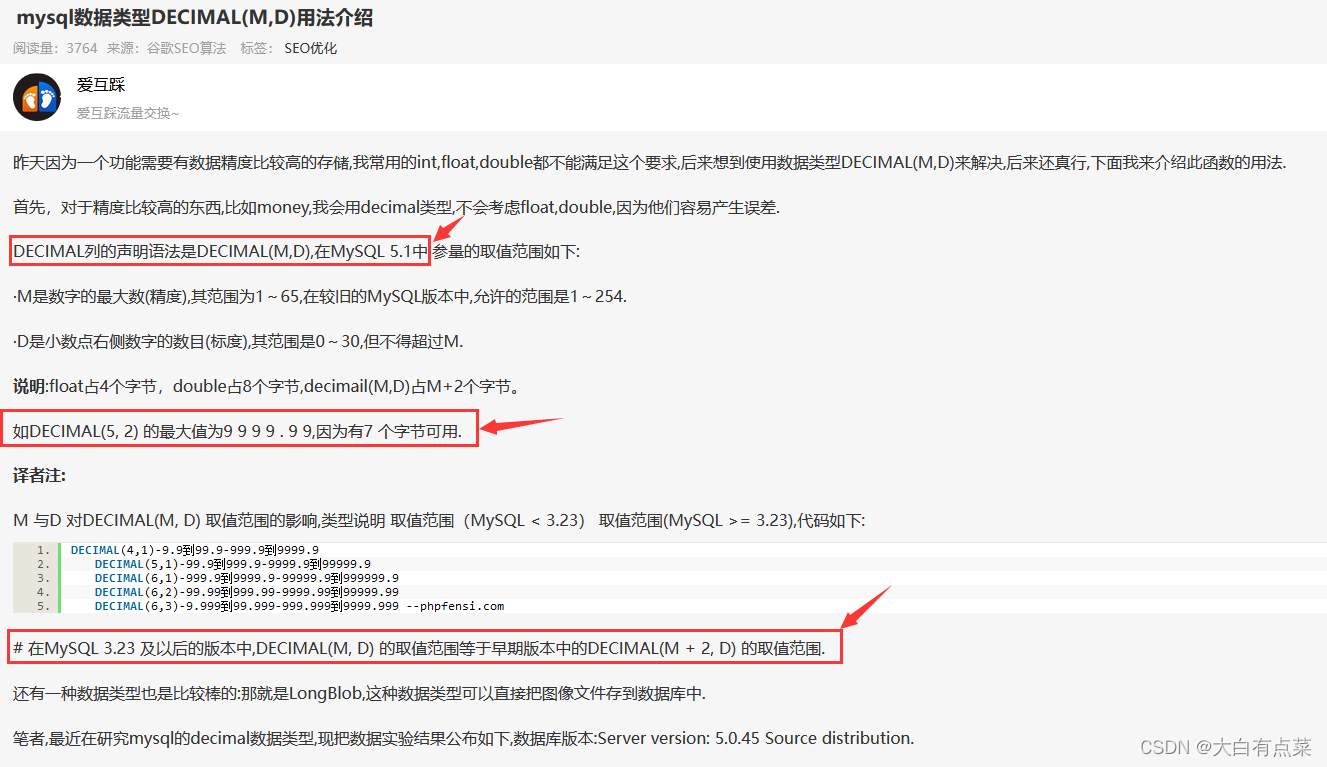

笔者从网上博客,总结出其他博主要表达的几点意思:
(1)
DECIMAL(M,D)是在MySQL 5.1引入的。
(2)DECIMAL(M,D)的占用字节数是M + 2。
真的是这样吗?其实啊,网上有太多太多这样的博客,人云亦云,别人说点东西,自己就把里面的内容当做权威,然后自己也写一篇这样类似的博客,却从来不去探究博客内容有没有问题,传递各种错误信息,这很害人啊!写技术类的文档,应该要以官网文档为根据,要做到博客内容有理有据,不睁眼说瞎话。好了,回归正题,笔者能力也有限,希望广大读者指出错误。
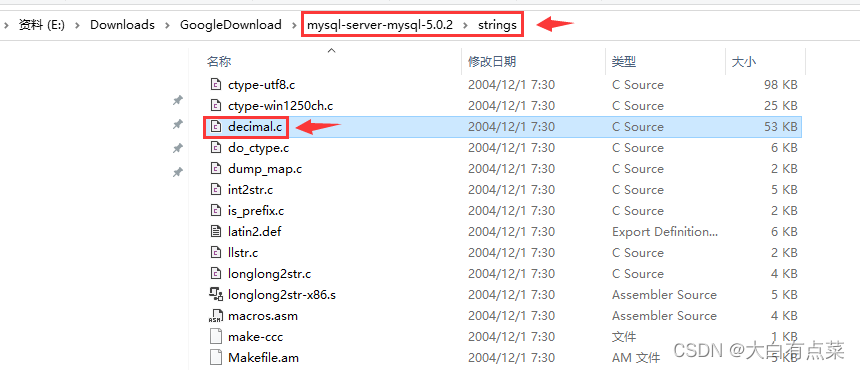
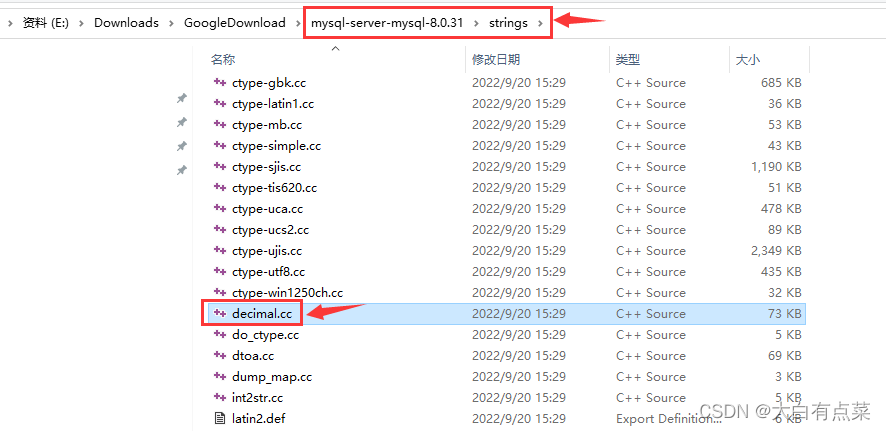
经过笔者研究,DECIMAL(M,D) 是在 MySQL 5 引入的,确切地说,是在 MySQL-5.0.2 版本引入的,一直到最新的 MySQL-8.0.31 ,源代码有经过不少修改,就是说 MySQL-5.0.1 和之前的版本都不存在 DECIMAL(M,D) 。有读者就不服了,你怎么知道的?当然是笔者下载N多版本的源码,一个个去找的呀,找出来 MySQL-5.0.1 并不存在 decimal.c 文件,而是在 MySQL-5.0.2 出现了!
DECIMAL(M,D) 是 decimal.c 或 decimal.cc 中定义的方法,这里需要注意,MySQL-5.0.2 源码包中 decimal.c 文件后缀是“.c”,但在最新的 MySQL-8.0.31 源码包中 decimal.cc 文件后缀却变为了“.cc”。无论是 decimal.c 或 decimal.cc 文件,都是在源码包的 strings 目录下。
github上MySQL各版本源码下载:
mysql-5.0.1源码:https://github.com/mysql/mysql-server/releases/tag/mysql-5.0.1
mysql-5.0.2源码:https://github.com/mysql/mysql-server/releases/tag/mysql-5.0.2
mysql-8.0.31源码:https://github.com/mysql/mysql-server/releases/tag/mysql-8.0.31

那么目前MySQL官网是如何介绍 DECIMAL 数据类型特征的呢?笔者也发现,官网只能查 5.6、5.7和8.0 三个版本的文档,前面低版本的文档查询不到了,不知是移除了还是放到别的位置。
【关于 DECIMAL 数据类型特征的官方文档介绍,从上到下是 8.0 、5.7、5.6】:
https://dev.mysql.com/doc/refman/8.0/en/precision-math-decimal-characteristics.html
https://dev.mysql.com/doc/refman/5.7/en/precision-math-decimal-characteristics.html
https://dev.mysql.com/doc/refman/5.6/en/precision-math-decimal-characteristics.html
官网都是英文,对于英语差的人,简直是天书而不可窥也!这可难不倒笔者我,特意使用浏览器的划词翻译(需要收费,WX一个月5元,一年45元,谷歌翻译功能需要特别方法,笔者喜欢这款插件是因为翻译后支持中英文同时显示)插件为大家友好地服务。谷歌翻译已经退出中国导致正常插件无法使用,但方法总比困难多是吧。

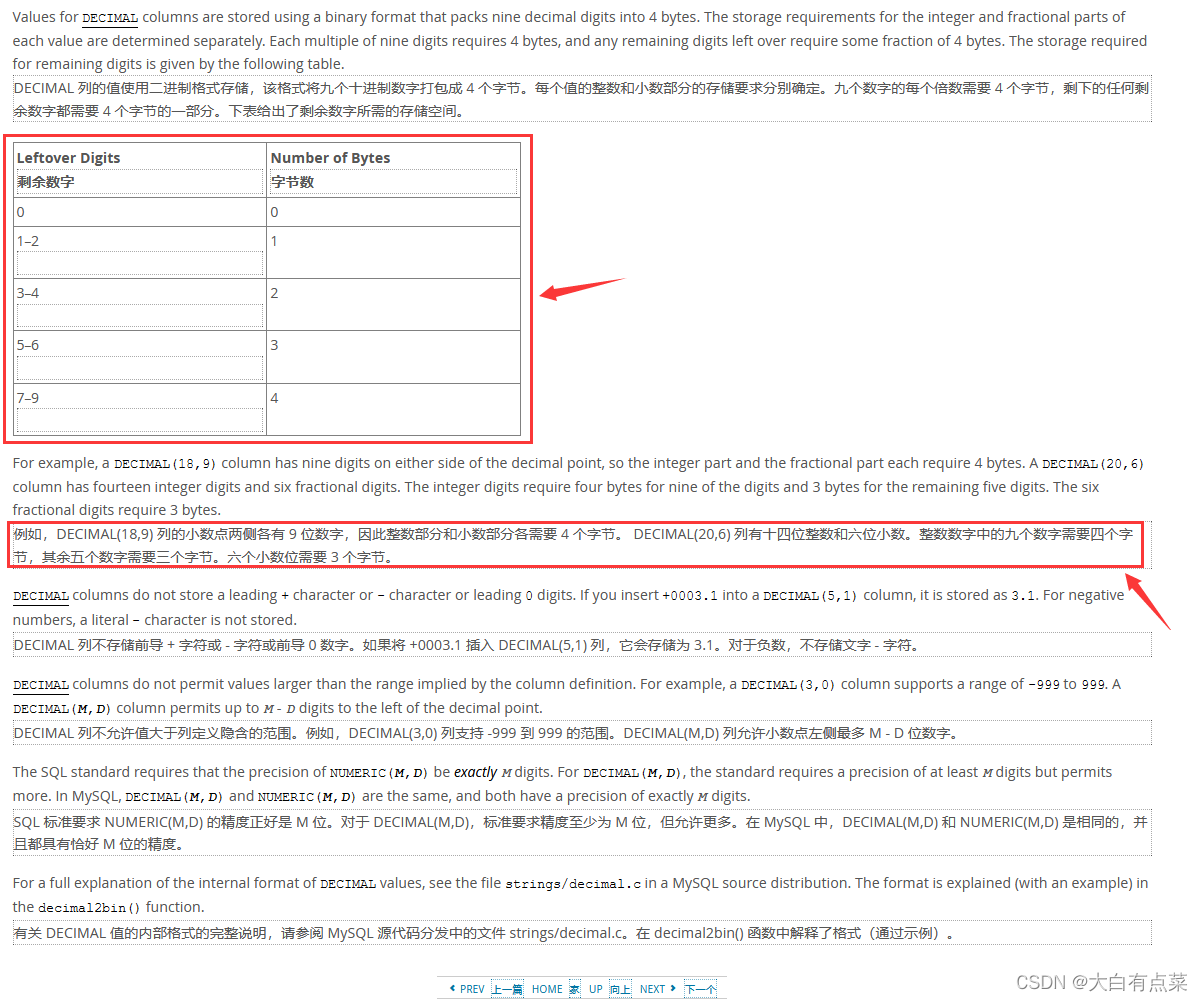
官网中提到,例子 DECIMAL(18,9) 中,整数部分有(18 - 9 = 9)个数字,小数部分有9个数字,那么9个数字占用4字节,两部分一共占用(4 + 4 = 8)字节。再来一个例子,DECIMAL(20,6) 中整数部分有14个数字,小数部分只有6个数字,14拆分为9和5,由于剩余数字个数是5到6之间,所以占用3字节,DECIMAL(20,6) 总的占用字节为(4 + 3 + 3 = 10)。
| 剩余数字 | 字节数 |
|---|---|
| 0 | 0 |
| 1-2 | 1个 |
| 3-4 | 2个 |
| 5-6 | 3个 |
| 7-9 | 4个 |
难道其它博客中写到的 DECIMAL(M,D) 占用字节为 M+2 是错误的吗?按那些博客的逻辑,DECIMAL(18,9)占用字节应该为20字节,DECIMAL(20,6)占用字节应该为22字节了,这和官方文档说的完全不一样啊!
其实,笔者认为,那些博客中写到的关于 DECIMAL 字节占用计算不一定就是错误的,应该旧版本就是这么处理的,不然总不能空穴来风,乱说一通吧?随着版本升级,有些数值逻辑处理可能导致各种问题,官方肯定是要优化算法的。笔者只能说,那些博客都是各种抄,有些东西过时了,也不自己去研究一下。学习就要紧跟时代步伐,多看看官方文档才能掌握更多新知识,不要随便将别人的文章当权威!
MySQL源码中,DECIMAL(M,D) 是怎么将 decimal 转换为 二进制 的呢?由于 decimal.c 或 decimal.cc 是用 c++ 去写的,这门编程语言笔者早就还给大一老师了,所以也看不懂,但是方法上面的注解中有个例子,可以拿出来讲解,相信读者们都能容易理解 decimal 转换为 二进制 的过程。
【MySQL-8.0.31源码中的 decimal.cc 文件中的 decimal2bin 方法核心代码】:
/* Convert decimal to its binary fixed-length representation two representations of the same length can be compared with memcmp with the correct -1/0/+1 result SYNOPSIS decimal2bin() from - value to convert to - points to buffer where string representation should be stored precision/scale - see decimal_bin_size() below NOTE the buffer is assumed to be of the size decimal_bin_size(precision, scale) RETURN VALUE E_DEC_OK/E_DEC_TRUNCATED/E_DEC_OVERFLOW DESCRIPTION for storage decimal numbers are converted to the "binary" format. This format has the following properties: 1. length of the binary representation depends on the {precision, scale} as provided by the caller and NOT on the intg/frac of the decimal to convert. 2. binary representations of the same {precision, scale} can be compared with memcmp - with the same result as decimal_cmp() of the original decimals (not taking into account possible precision loss during conversion). This binary format is as follows: 1. First the number is converted to have a requested precision and scale. 2. Every full DIG_PER_DEC1 digits of intg part are stored in 4 bytes as is 3. The first intg % DIG_PER_DEC1 digits are stored in the reduced number of bytes (enough bytes to store this number of digits - see dig2bytes) 4. same for frac - full decimal_digit_t's are stored as is, the last frac % DIG_PER_DEC1 digits - in the reduced number of bytes. 5. If the number is negative - every byte is inversed. 5. The very first bit of the resulting byte array is inverted (because memcmp compares unsigned bytes, see property 2 above) Example: 1234567890.1234 internally is represented as 3 decimal_digit_t's 1 234567890 123400000 (assuming we want a binary representation with precision=14, scale=4) in hex it's 00-00-00-01 0D-FB-38-D2 07-5A-EF-40 now, middle decimal_digit_t is full - it stores 9 decimal digits. It goes into binary representation as is: ........... 0D-FB-38-D2 ............ First decimal_digit_t has only one decimal digit. We can store one digit in one byte, no need to waste four: 01 0D-FB-38-D2 ............ now, last digit. It's 123400000. We can store 1234 in two bytes: 01 0D-FB-38-D2 04-D2 So, we've packed 12 bytes number in 7 bytes. And now we invert the highest bit to get the final result: 81 0D FB 38 D2 04 D2 And for -1234567890.1234 it would be 7E F2 04 C7 2D FB 2D */ int decimal2bin(const decimal_t *from, uchar *to, int precision, int frac) { dec1 mask = from->sign ? -1 : 0, *buf1 = from->buf, *stop1; int error = E_DEC_OK, intg = precision - frac, isize1, intg1, intg1x, from_intg, intg0 = intg / DIG_PER_DEC1, frac0 = frac / DIG_PER_DEC1, intg0x = intg - intg0 * DIG_PER_DEC1, frac0x = frac - frac0 * DIG_PER_DEC1, frac1 = from->frac / DIG_PER_DEC1, frac1x = from->frac - frac1 * DIG_PER_DEC1, isize0 = intg0 * sizeof(dec1) + dig2bytes[intg0x], fsize0 = frac0 * sizeof(dec1) + dig2bytes[frac0x], fsize1 = frac1 * sizeof(dec1) + dig2bytes[frac1x]; const int orig_isize0 = isize0; const int orig_fsize0 = fsize0; uchar *orig_to = to; buf1 = remove_leading_zeroes(from, &from_intg); if (unlikely(from_intg + fsize1 == 0)) { mask = 0; /* just in case */ intg = 1; buf1 = &mask; } intg1 = from_intg / DIG_PER_DEC1; intg1x = from_intg - intg1 * DIG_PER_DEC1; isize1 = intg1 * sizeof(dec1) + dig2bytes[intg1x]; if (intg < from_intg) { buf1 += intg1 - intg0 + (intg1x > 0) - (intg0x > 0); intg1 = intg0; intg1x = intg0x; error = E_DEC_OVERFLOW; } else if (isize0 > isize1) { while (isize0-- > isize1) *to++ = (char)mask; } if (fsize0 < fsize1) { frac1 = frac0; frac1x = frac0x; error = E_DEC_TRUNCATED; } else if (fsize0 > fsize1 && frac1x) { if (frac0 == frac1) { frac1x = frac0x; fsize0 = fsize1; } else { frac1++; frac1x = 0; } } /* intg1x part */ if (intg1x) { int i = dig2bytes[intg1x]; dec1 x = mod_by_pow10(*buf1++, intg1x) ^ mask; switch (i) { case 1: mi_int1store(to, x); break; case 2: mi_int2store(to, x); break; case 3: mi_int3store(to, x); break; case 4: mi_int4store(to, x); break; default: assert(0); } to += i; } /* intg1+frac1 part */ for (stop1 = buf1 + intg1 + frac1; buf1 < stop1; to += sizeof(dec1)) { dec1 x = *buf1++ ^ mask; assert(sizeof(dec1) == 4); mi_int4store(to, x); } /* frac1x part */ if (frac1x) { dec1 x; int i = dig2bytes[frac1x], lim = (frac1 < frac0 ? DIG_PER_DEC1 : frac0x); while (frac1x < lim && dig2bytes[frac1x] == i) frac1x++; x = div_by_pow10(*buf1, DIG_PER_DEC1 - frac1x) ^ mask; switch (i) { case 1: mi_int1store(to, x); break; case 2: mi_int2store(to, x); break; case 3: mi_int3store(to, x); break; case 4: mi_int4store(to, x); break; default: assert(0); } to += i; } if (fsize0 > fsize1) { uchar *to_end = orig_to + orig_fsize0 + orig_isize0; while (fsize0-- > fsize1 && to < to_end) *to++ = (uchar)mask; } orig_to[0] ^= 0x80; /* Check that we have written the whole decimal and nothing more */ assert(to == orig_to + orig_fsize0 + orig_isize0); return error; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
使用谷歌进行 decimal2bin 方法上标注的注解翻译,得到以下内容。
将十进制转换为其二进制固定长度表示相同长度的两个表示可以用 memcmp 进行比较正确的 -1/0/+1 结果
概要(SYNOPSIS)
decimal2bin()
from - 要转换的值
to - 指向应存储字符串表示的缓冲区
精度/比例 - 请参见下面的 decimal_bin_size()
笔记(NOTE)
假定缓冲区的大小为 decimal_bin_size(precision, scale)
返回值(RETURN VALUE)
E_DEC_OK/E_DEC_TRUNCATED/E_DEC_OVERFLOW
描述(DESCRIPTION)
用于存储的十进制数被转换为“二进制”格式。
此格式具有以下属性:
1.二进制表示的长度取决于{precision, scale}由调用者提供,而不是在小数点的 intg/frac 上转换。
2. 可以将相同 {precision, scale} 的二进制表示与 memcmp 进行比较 - 结果与原始小数的 decimal_cmp() 相同
(不考虑转换过程中可能出现的精度损失)。
这个二进制格式如下:
1.首先将数字转换为具有要求的精度和小数位数。
2.intg 部分的每个完整 DIG_PER_DEC1 数字都按原样存储在 4 个字节中。
3.第一个 intg % DIG_PER_DEC1 数字存储在减少的字节数中(足够的字节来存储这个数字(digits)数量——见 dig2bytes)
4.对于 frac 也是如此 - 完整的 decimal_digit_t 按原样存储,最后一个 frac % DIG_PER_DEC1 数字 - 在减少的字节数中。
5.如果数字是负数 - 每个字节都被反转。
5.结果字节数组的第一位被反转(因为 memcmp 比较无符号字节,参见上面的属性 2)。
笔者将注解中的例子抽出来,使用谷歌进行翻译,得到以下内容。
例子:
1234567890.1234
内部表示为 3 个 decimal_digit_t
1234567890123400000
(假设我们想要一个精度为 14,比例为 4 的二进制表示)
十六进制是
00-00-00-010D-FB-38-D207-5A-EF-40
现在,中间的 decimal_digit_t 已满 - 它存储 9 个十进制数字。 它去按原样转换为二进制表示形式:
…0D-FB-38-D2…
第一个 decimal_digit_t 只有一个十进制数字。 我们可以存储一个数字一个字节,不需要浪费四个:
010D-FB-38-D2…
现在,最后一位。 它是123400000。我们可以用两个字节存储1234:
010D-FB-38-D204-D2
所以,我们在 7 个字节中打包了 12 个字节的数字。
现在我们反转最高位以获得最终结果:
810DFB38D204D2
对于-1234567890.1234它将是
7EF204C72DFB2D
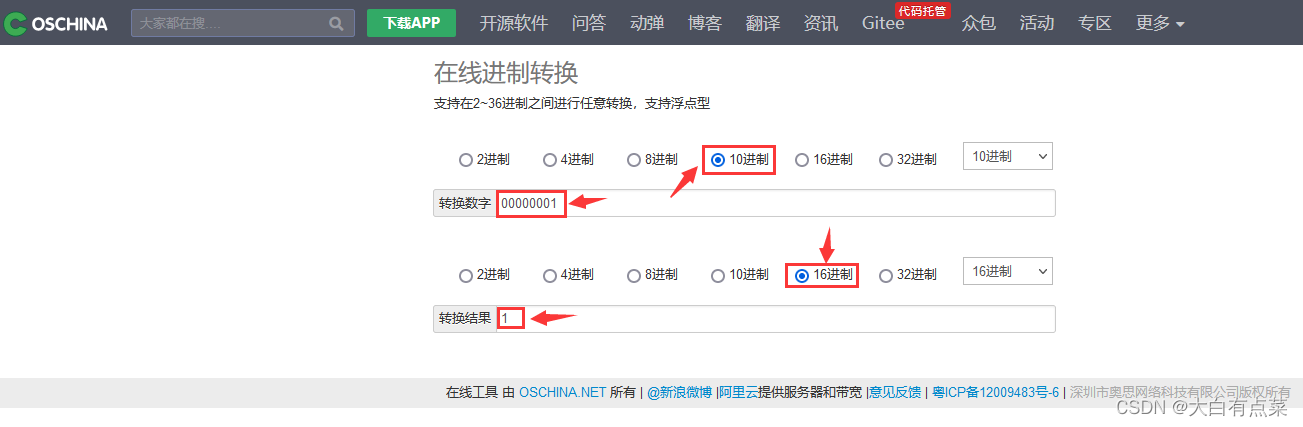
例子中,将 1234567890.1234 这个定点数分解为三部分:1、234567890、1234 ,每部分凑够9个数字,不够的就补0,最后得到以下新的三部分:1、234567890、123400000。我们可以使用第三方网站在线进制转换,如 oschina.net 中的在线进制转换:https://tool.oschina.net/hexconvert 。
将十进制的 1 转换为 十六进制 形式,得到结果为 1 ,可以写作:00-00-00-01 。
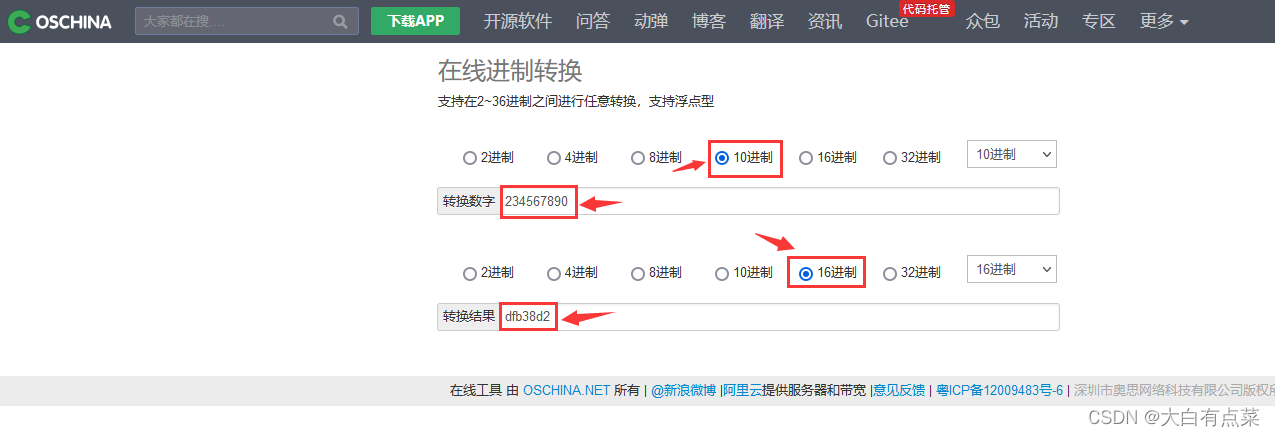
将十进制的 234567890 转换为 十六进制 形式,得到结果为 dfb38d2 ,可以写作:0D-FB-38-D2 。
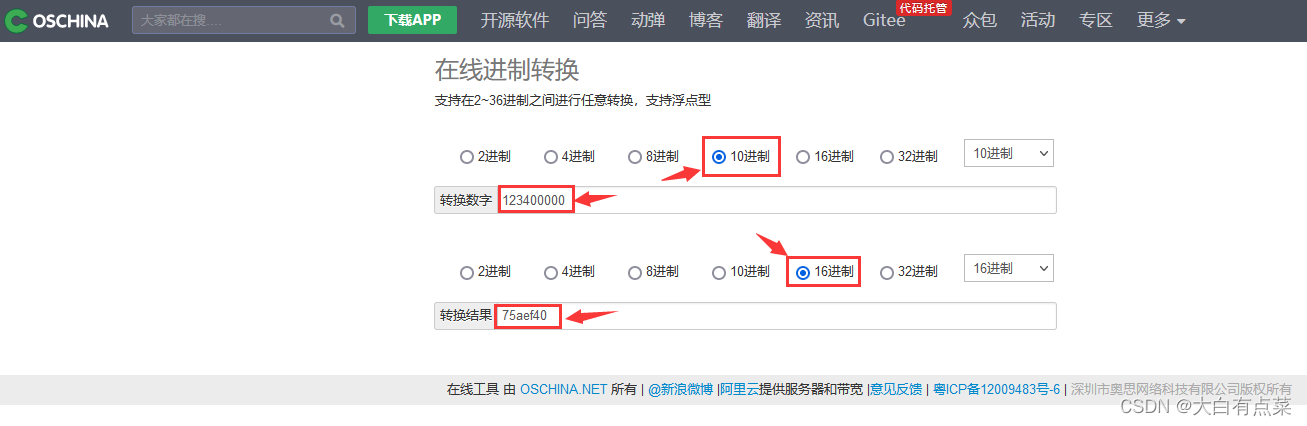
将十进制的 123400000 转换为 十六进制 形式,得到结果为 75aef40 ,可以写作:07-5A-EF-40 。
00-00-00-01 如果使用4个字节存储会很浪费,只有一个数字1,使用1个字节存储就可以了。
0D-FB-38-D2 使用4个字节存储。
1234 只有4个数字,如果使用4个字节存储也很浪费,所以直接对 1234 进行 十六进制转换,如下图所示,得到 4d2 ,写作:04-D2 。这样使用2个字节存储。
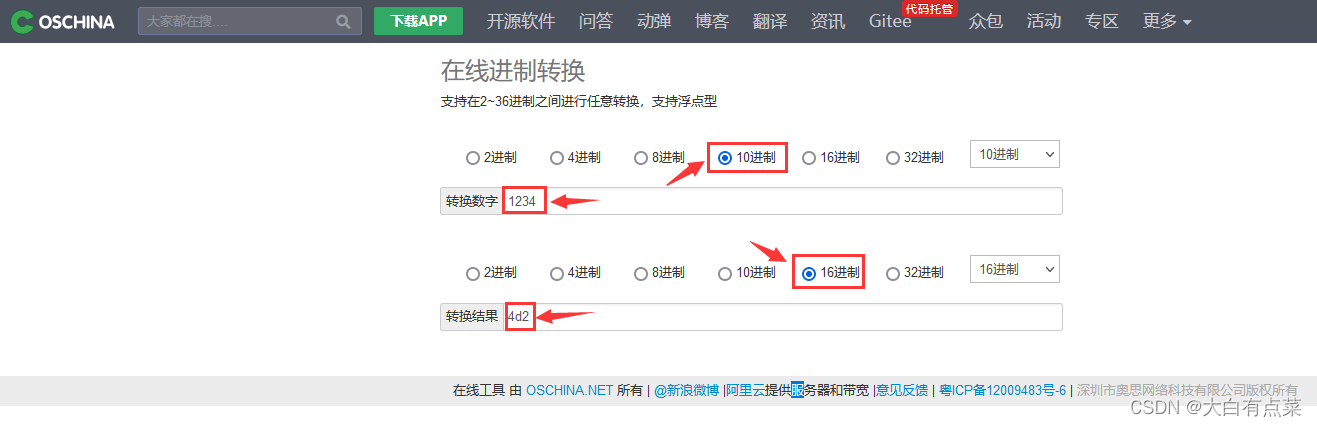
由上面的结果,得到:01 0D FB 38 D2 04 D2 ,这还不是最终的结果,还需要对最高位(01)进行反转。如何反转呢?使用(10000000)和 01 的二进制(00000001)进行异或运算,0 + 0 = 0,0 + 1 = 1,1 + 0 = 1,1 + 1 = 0,最终得到二进制数 10000001 ,转换为 十六进制 ,得到结果:81 。
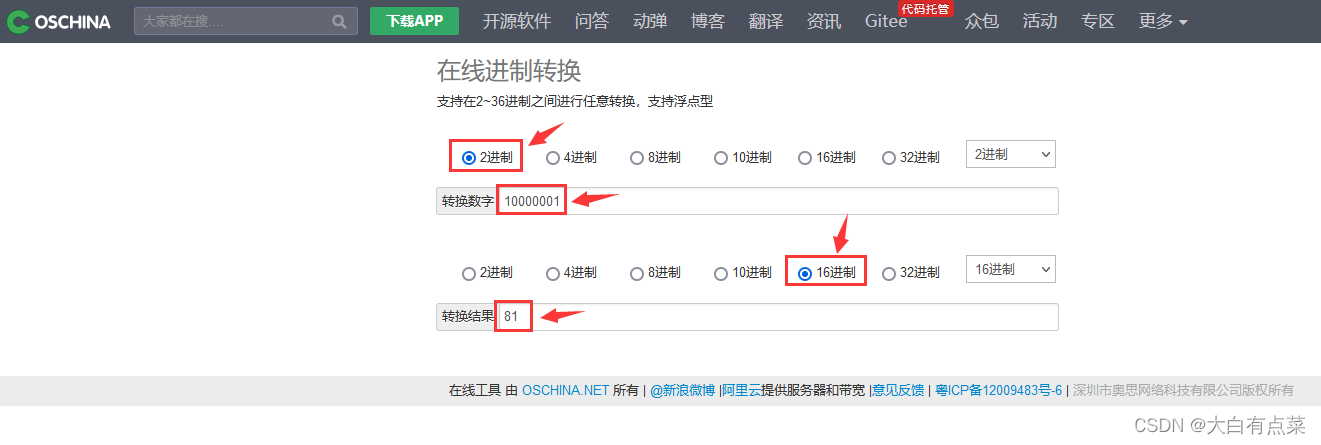
最终结果是:81 0D FB 38 D2 04 D2 。使用 1 + 4 + 2 = 7 个字节就实现了 1234567890.1234 的存储。
如果是负数 -1234567890.1234 呢?
同样将负数 -1234567890.1234 分解为三个部分,先忽略前面的负号。由正数的处理过程,同样得到 01 0D FB 38 D2 04 D2 7个十六进制数。负数的反转稍微复杂,如下表所示。
| 十六进制数 | 转换为二进制数 | 负数是所有二进制数最高位取反得到负数原码 | 负数反码是原码的最高位不变,其它位取反 | 反码对应的十六进制 | 最高位再取反(反转) | 最终结果(十六进制) |
|---|---|---|---|---|---|---|
| 01 | 00000001 | 10000001 | 11111110 | FE | 01111110,即 7E | 7E |
| 0D | 00001101 | 10001101 | 11110010 | F2 | F2 | |
| FB | 11111011 | 01111011 | 00000100 | 04 | 04 | |
| 38 | 00111000 | 10111000 | 11000111 | C7 | C7 | |
| D2 | 11010010 | 01010010 | 00101101 | 2D | 2D | |
| 04 | 00000100 | 10000100 | 11111011 | FB | FB | |
| D2 | 11010010 | 01010010 | 00101101 | 2D | 2D |
负数 -1234567890.1234 的最终结果为:7E F2 04 C7 2D FB 2D 。




