[力扣]根据前中序构造二叉树--详细解析

根据前中序遍历顺序构建一个二叉树

力扣练习链接

过程

总体框架

• 设preorder的左边界为pleft,右边界为pright[注意这里是闭区间能取到]
• 同时设inorder的左边界为ileft,有边界为iright[同样也是可以取到的索引区间]
• 我们生成每一个区间的树的头结点,然后向上返回,对于他的父亲结点,利用子树的返回值作为左右子节点

递归结构的设计

当区间内只有一个结点，继续遍历，直到区间取到空的树判断是否结束

• 如果遍历到的右子树是空的,那么下一次会出现这种情况:ileft>iright

• 同样的,如果左子树是空的,那么下一次会出现:iright<ileft
  所以结束条件这样去设计：

  if (ileft>iright||iright<ileft) return nullptr;

  去返回一个空的指针

寻找左右子树

1. 对于以前序和中序遍历的树,他的结构如下:
   

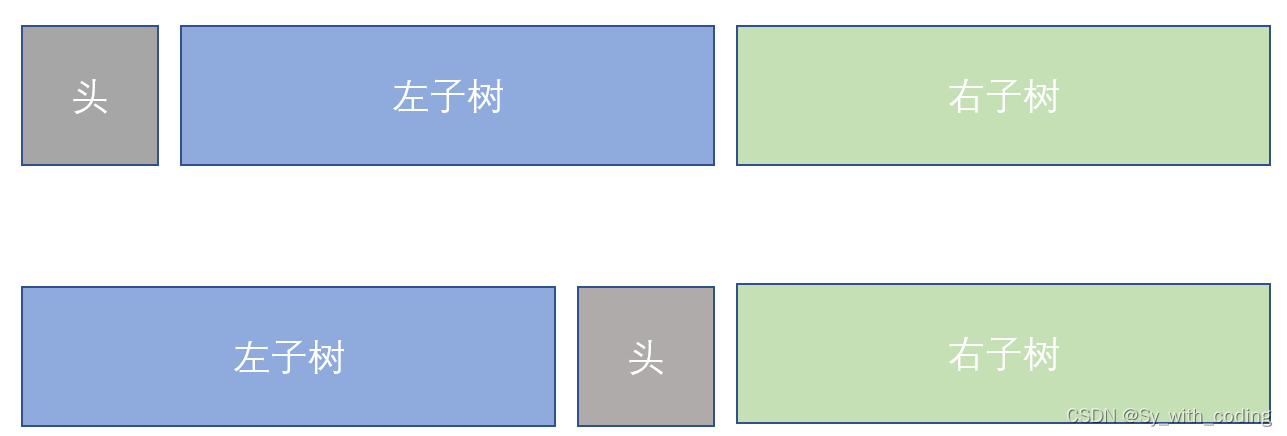
   遍历一遍 inorder 数组, 将所有的元素的以<元素值, 索引值>的结构存入哈希表中
   根结点的值就是inorder数组中的首元素
   但是我们需要在preorder中去找到根节点的索引位置
   通过之前构建哈希表,我们可以直接用头结点的值来得到它在inorder数组中的索引下标
   以左子树的区间为例, 在inorder和preorder区间中的长度相等,所以可以得到这样的等式:
   

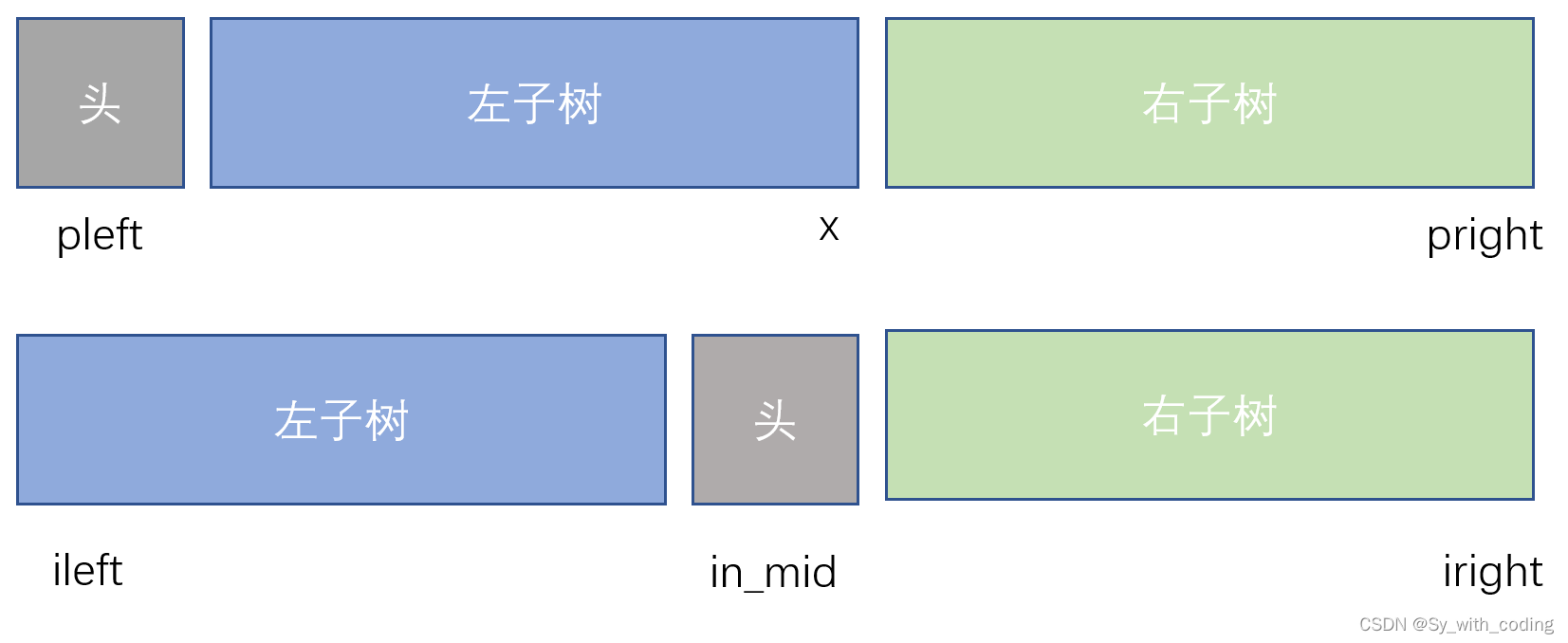
   in_mid-ileft = x - pleft

2. 这样我们就得到了左子树的区间,preorder:[pleft+1, x]
   ineorder:[ileft, in_mid-1]

3. 同样的,对于右子树的区间,preorder:[x+1, pright]
   ineorder:[in_mid+1, iright]

Coding

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> hash;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int size = preorder.size();
        for (int i = 0; i < size; i++) {
            hash[inorder[i]] = i;
        }
        return f(preorder, inorder, 0, size-1, 0, size-1);
    }
    TreeNode* f(vector<int>& preorder, vector<int>& inorder, int pleft, int pright, int ileft, int iright) {
        if (ileft>iright || iright<ileft) {
            return nullptr;
        }
        int pleftValue = preorder[pleft];
        TreeNode* root = new TreeNode(pleftValue);
        int in_mid = hash[pleftValue];
        int x = pleft + in_mid - ileft;
        root->left = f(preorder, inorder, pleft+1, x, ileft, in_mid-1);
        root->right = f(preorder, inorder, x+1, pright, in_mid+1, iright);
        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34