我家小花儿

这个屌丝很懒，什么也没留下！

热门标签

【机器学习】马尔可夫（Markov）预测法整理_马尔科夫预测能解决哪些类型的问题

作者：我家小花儿 | 2024-04-07 20:06:52

踩

马尔科夫预测能解决哪些类型的问题

隐马尔可夫模型（Hidden Markov Model，HMM）作为一种统计分析模型，创立于20世纪70年代。80年代得到了传播和发展，成为信号处理的一个重要方向，现已成功地用于语音识别，行为识别，文字识别以及故障诊断等领域。

基本理论

隐马尔可夫模型是马尔可夫链的一种，它的状态不能直接观察到，但能通过观测向量序列观察到，每个观测向量都是通过某些概率密度分布表现为各种状态，每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以，隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。自20世纪80年代以来，HMM被应用于语音识别，取得重大成功。到了90年代，HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。HMM在生物信息科学、故障诊断等领域也开始得到应用。

基本算法

针对以下三个问题，人们提出了相应的算法

*1 评估问题：前向算法

*2 解码问题： Viterbi算法

*3 学习问题： Baum-Welch算法(向前向后算法) [1]

基本概述

一种HMM可以呈现为最简单的动态贝叶斯网络。隐马尔可夫模型背后的数学是由LEBaum和他的同事开发的。它与早期由RuslanL.Stratonovich提出的最优非线性滤波问题息息相关，他是第一个提出前后过程这个概念的。

在简单的马尔可夫模型（如马尔可夫链），所述状态是直接可见的观察者，因此状态转移概率是唯一的参数。在隐马尔可夫模型中，状态是不直接可见的，但输出依赖于该状态下，是可见的。每个状态通过可能的输出记号有了可能的概率分布。因此，通过一个HMM产生标记序列提供了有关状态的一些序列的信息。注意，“隐藏”指的是，该模型经其传递的状态序列，而不是模型的参数；即使这些参数是精确已知的，我们仍把该模型称为一个“隐藏”的马尔可夫模型。隐马尔可夫模型以它在时间上的模式识别所知，如语音，手写，手势识别，词类的标记，乐谱，局部放电和生物信息学应用。

隐马尔可夫模型可以被认为是一个概括的混合模型中的隐藏变量（或变量），它控制的混合成分被选择为每个观察，通过马尔可夫过程而不是相互独立相关。最近，隐马尔可夫模型已推广到两两马尔可夫模型和三重态马尔可夫模型，允许更复杂的数据结构的考虑和非平稳数据建模。

模型表达

隐马尔可夫模型（HMM）可以用五个元素来描述，包括2个状态集合和3个概率矩阵：

1. 隐含状态 S

这些状态之间满足马尔可夫性质，是马尔可夫模型中实际所隐含的状态。这些状态通常无法通过直接观测而得到。（例如S1、S2、S3等等)

2. 可观测状态 O

在模型中与隐含状态相关联，可通过直接观测而得到。

(例如O1、O2、O3等等，可观测状态的数目不一定要和隐含状态的数目一致。）

3. 初始状态概率矩阵 π

表示隐含状态在初始时刻t=1的概率矩阵，(例如t=1时，P(S1)=p1、P(S2)=P2、P(S3)=p3，则初始状态概率矩阵 π=[ p1 p2 p3 ].

4. 隐含状态转移概率矩阵 A。

描述了HMM模型中各个状态之间的转移概率。

其中Aij = P( Sj | Si ),1≤i,,j≤N.

表示在 t 时刻、状态为 Si 的条件下，在 t+1 时刻状态是 Sj 的概率。

5. 观测状态转移概率矩阵 B （英文名为Confusion Matrix，直译为混淆矩阵不太易于从字面理解）。

令N代表隐含状态数目，M代表可观测状态数目，则：

Bij = P( Oi | Sj ), 1≤i≤M,1≤j≤N.

表示在 t 时刻、隐含状态是 Sj 条件下，观察状态为 Oi 的概率。

总结：一般的，可以用λ=(A,B,π)三元组来简洁的表示一个隐马尔可夫模型。隐马尔可夫模型实际上是标准马尔可夫模型的扩展，添加了可观测状态集合和这些状态与隐含状态之间的概率关系。

基本问题

1. 评估问题。

给定观测序列 O=O1O2O3…Ot和模型参数λ=(A,B,π)，怎样有效计算某一观测序列的概率，进而可对该HMM做出相关评估。例如，已有一些模型参数各异的HMM，给定观测序列O=O1O2O3…Ot，我们想知道哪个HMM模型最可能生成该观测序列。通常我们利用forward算法分别计算每个HMM产生给定观测序列O的概率，然后从中选出最优的HMM模型。

这类评估的问题的一个经典例子是语音识别。在描述语言识别的隐马尔科夫模型中，每个单词生成一个对应的HMM，每个观测序列由一个单词的语音构成，单词的识别是通过评估进而选出最有可能产生观测序列所代表的读音的HMM而实现的。

2.解码问题

给定观测序列 O=O1O2O3…Ot 和模型参数λ=(A,B,π)，怎样寻找某种意义上最优的隐状态序列。在这类问题中，我们感兴趣的是马尔科夫模型中隐含状态，这些状态不能直接观测但却更具有价值，通常利用Viterbi算法来寻找。

这类问题的一个实际例子是中文分词，即把一个句子如何划分其构成才合适。例如，句子“发展中国家”是划分成“发展-中-国家”，还是“发展-中国-家”。这个问题可以用隐马尔科夫模型来解决。句子的分词方法可以看成是隐含状态，而句子则可以看成是给定的可观测状态，从而通过建HMM来寻找出最可能正确的分词方法。

3. 学习问题。

即HMM的模型参数λ=(A,B,π)未知，如何调整这些参数以使观测序列O=O1O2O3…Ot的概率尽可能的大。通常使用Baum-Welch算法以及Reversed Viterbi算法解决。

怎样调整模型参数λ=(A,B,π)，使观测序列 O=O1O2O3…Ot的概率最大？


import nltk
from nltk.corpus import brown
'''
# 在 terminal 里输入 nltk.download() 即可下载相应的所需包
Natural Language Toolkit 自然语言处理工具包，在NLP领域中，最常使用的一个Python库。
NLTK是一个开源的项目，包含:Python模块，数据集和教程，用于NLP的研究和开发。
NLTK由Steven Bird和Edward Loper在宾夕法尼亚大学计算机和信息科学系开发。
NLTK包括图形演示和示例数据。其提供的教程解释了工具包支持的语言处理任务背后的基本概念。
'''
'''
HMM实例-进行词性标注【用NLTK自带的Brown词库进行学习】
单词集 words = w1 ... wN
Tag集 tags = t1 ... tN
P(tags | words) 正比于 P(ti | t{i-1}) * P(wi | ti)
为了找一个句子的tag，其实就是找最好的一套tags，让它最能够符合给定的单词(words)。
'''
'''
（1）预处理词库 【做预处理，即给 words 加上开始和结束符号】
Brown 里的句子都是已标注好的( 单词 , 词性 )，词性包括：NOUN 名词、VERB 动词 等。
长这个样子 (I , NOUN), (LOVE, VERB), (YOU, NOUN) # I 名词
那么，我们的开始符号也得跟他的格式符合，用 (START, START) (END, END) 来表示
'''
brown_tags_words = []
for sent in brown.tagged_sents():
    brown_tags_words.append(("START", "START")) # 先加开头
    # 把tag都省略成前两个字母 tag[:2]
    brown_tags_words.extend([(tag[:2], word) for (word, tag) in sent])
    brown_tags_words.append(("END", "END")) # 加个结尾
 
'''
（2）词统计，将所有的词库中的 word单词 与 tag 之间的关系，做个简单粗暴的统计。
也就是之前提到的：P(wi | ti) = count(wi, ti) / count(ti)
你可以一个个的 loop 全部的 corpus 语料库，使用NLTK自带统计工具
nltk.ConditionalFreqDist 条件频率分布 conditional frequency distribution
nltk.ConditionalProbDist 条件概率分布 conditional probability distribution
'''
cfd_tagwords = nltk.ConditionalFreqDist(brown_tags_words)
cpd_tagwords = nltk.ConditionalProbDist(cfd_tagwords, nltk.MLEProbDist)
print("The probability of an adjective (JJ) being 'new' is", cpd_tagwords["JJ"].prob("new"))
# 形容词（JJ）为“new”的概率是      prob 概率的简写
print("The probability of a verb (VB) being 'duck' is", cpd_tagwords["VB"].prob("duck"))
'''
（3）计算公式：P(ti | t{i-1}) = count(t{i-1}, ti) / count(t{i-1})
这个公式跟words没有什么卵关系。它是属于隐层的马科夫链。
nltk.bigrams二元随机存储器，将前后两个一组，联在一起
'''
brown_tags = [tag for (tag, word) in brown_tags_words]  #获取所有tag
cfd_tags = nltk.ConditionalFreqDist(nltk.bigrams(brown_tags)) # count(t{i-1} , ti)
cpd_tags = nltk.ConditionalProbDist(cfd_tags, nltk.MLEProbDist) # P(ti | t{i-1})
print("If we have just seen 'DT', the probability of 'NN' is", cpd_tags["DT"].prob("NN"))
print("If we have just seen 'VB', the probability of 'JJ' is", cpd_tags["VB"].prob("DT"))
print("If we have just seen 'VB', the probability of 'NN' is", cpd_tags["VB"].prob("NN"))
'''
一些有趣的结果：比如， 一句话 "I want to race"， 一套tag "PP VB TO VB"
他们之间的匹配度有多高呢？
其实就是：P(START) * P(PP|START) * P(I | PP) * P(VB | PP) * P(want | VB) *
        P(TO | VB) * P(to | TO) * P(VB | TO) * P(race | VB) * P(END | VB)
'''
prob_tagsequence = cpd_tags["START"].prob("PP") * cpd_tagwords["PP"].prob("I") * \
                   cpd_tags["PP"].prob("VB") * cpd_tagwords["VB"].prob("want") * \
                   cpd_tags["VB"].prob("TO") * cpd_tagwords["TO"].prob("to") * \
                   cpd_tags["TO"].prob("VB") * cpd_tagwords["VB"].prob("race") * \
                   cpd_tags["VB"].prob("END")
 
print("The probability of the tag sequence 'START PP VB TO VB END' for 'I want to race' is:", prob_tagsequence)
 
'''
（4）维特比 Viterbi 的实现  --  如果有一句话，怎么计算最符合的tag是哪组呢？
首先，拿出所有独特的tags（也就是tags的全集）
'''
distinct_tags = set(brown_tags)  # distinct 不同的
sentence = ["I", "want", "to", "race"] # 我想参加比赛
sentlen = len(sentence)
'''
接下来，开始维特比：从1循环到句子的总长N，记为i。每次都找出以tag X为最终节点，长度为i的tag链。
'''
viterbi = []
'''
同时，还需要一个回溯器：从1循环到句子的总长N，记为i。把所有tag X 前一个Tag记下来。
'''
backpointer = []
first_viterbi = {}
first_backpointer = {}
for tag in distinct_tags:
    if tag == "START": continue # don't record anything for the START tag
    first_viterbi[tag] = cpd_tags["START"].prob(tag) * cpd_tagwords[tag].prob(sentence[0])
    first_backpointer[tag] = "START"
 
print(first_viterbi)
print(first_backpointer)
 
viterbi.append(first_viterbi)
backpointer.append(first_backpointer)
 
currbest = max(first_viterbi.keys(), key=lambda tag: first_viterbi[tag])
print("Word", "'" + sentence[0] + "'", "current best two-tag sequence:",
      first_backpointer[currbest], currbest)
 
for wordindex in range(1, len(sentence)):
    this_viterbi = {}
    this_backpointer = {}
    prev_viterbi = viterbi[-1]
 
    for tag in distinct_tags:
        if tag == "START": # START没啥卵用，要忽略
            continue
        '''
        如果现在这个tag是X，现在的单词是w，
        想找前一个tag Y，且让最好的 tag sequence 以 Y X 结尾。
        也就是说，Y要能最大化：prev_viterbi[ Y ] * P(X | Y) * P( w | X)
        '''
        best_previous = max(prev_viterbi.keys(),
                            key=lambda prevtag: prev_viterbi[prevtag] \
                                                * cpd_tags[prevtag].prob(tag) \
                                                * cpd_tagwords[tag].prob(sentence[wordindex]))
 
        this_viterbi[tag] = prev_viterbi[best_previous] \
                            * cpd_tags[best_previous].prob(tag) \
                            * cpd_tagwords[tag].prob(sentence[wordindex])
        this_backpointer[tag] = best_previous
 
    # 每次找完Y 都要把目前最好的 存一下
    currbest = max(this_viterbi.keys(), key=lambda tag: this_viterbi[tag])
    print("Word", "'" + sentence[wordindex] + "'", "current best two-tag sequence:"
          , this_backpointer[currbest], currbest)
 
    # 全部存下来
    viterbi.append(this_viterbi)
    backpointer.append(this_backpointer)
 
 
# 找所有以END结尾的tag sequence
prev_viterbi = viterbi[-1]
best_previous = max(prev_viterbi.keys(),
                    key=lambda prevtag: prev_viterbi[prevtag] * cpd_tags[prevtag].prob("END"))
 
prob_tagsequence = prev_viterbi[best_previous] * cpd_tags[best_previous].prob("END")
 
# 倒着存。。。。因为。。好的在后面
best_tagsequence = ["END", best_previous]
backpointer.reverse()
 
current_best_tag = best_previous
for bp in backpointer:
    best_tagsequence.append(bp[current_best_tag])
    current_best_tag = bp[current_best_tag]
 
best_tagsequence.reverse()
 
print("The sentence was:", end=" ") # end=" " print 输出不换行
for w in sentence: print(w, end=" ")
print("\n")
print("The best tag sequence is:", end=" ")
for t in best_tagsequence: print(t, end=" ")
print("\n")
print("The probability of the best tag sequence is:", prob_tagsequence)
# 最佳标签序列的概率为 5.71772824864617e-14

　马尔可夫（Markov）是俄国著名的数学家。马尔可夫预测法是以马尔可夫的名字命名的一种特殊的市场预测方法。马尔可夫预测法主要用于市场占有率的预测和销售期望利润的预测。就是一种预测事件发生的概率的方法。它是基于马尔可夫链，根据事件的目前状况预测其将来各个时刻（或时期）变动状况的一种预测方法。马尔可夫预测法是对地理、天气、市场、进行预测的基本方法，它是地理预测中常用的重要方法之一。

马尔可夫分析的基础原理

　　马尔可夫进行深入研究后指出!对于一个系统,由一个状态转至另一个状态的转换过程中,存在着转移概率,并且这种转移概率可以依据其紧接的前一种状态推算出来,与该系统的原始状态和此次转移前的过程无关。一系列的马尔可夫过程的整体称为马尔可夫链-马尔可夫过程的基本概念是研究系统的“状态”及状态的‘转移“,从一个状态转换到另一个状态的可能性,我们称之为状态转移概率-所有状态转移概率的排列即是转移概率矩阵

　　1.状态转移概率具有两个特性：

　　(1)P_ij\ge0(P_ij指从第i转向第j的概率)；

　　\sum_{j=1}P_ij=1

　　2.马尔可夫分析的基本假定

　　在进行马尔可夫分析时,我们假定：

　　(1)预测期系统状态数保持不变

　　(2)系统状态转移概率矩阵不随时间变化

　　(3)状态转移仅受前一状态影响,即马尔可夫过程的无后效性

　　3.马尔可夫过程用于预测基本步骤

　　首先确定系统状态,然后确定状态之间转移概率,再进行预测,并对预测结果进行分析-若结果合理,则可提交预测报告,否则需检查系统状态及状态转移概率是否正确。

什么是马尔可夫过程

　　事物的发展状态总是随着时间的推移而不断变化的。在一般情况下，人们要了解事物未来的发展状态，不但要看到事物现在的状态，还要看到事物过去的状态。马尔可夫认为，还存在另外一种情况，人们要了解事物未来的发展状态，只须知道事物现在的状态，而与事物以前的状态毫无关系。例如，Ａ产品明年是畅销还是滞销，只与今年的销售情况有关，而与往年的销售情况没有直接的关系。后者的这种情况就称为马尔可夫过程，前者的情况就属于非马尔可夫过程。

　　马尔可夫过程的重要特征是无后效性。事物第n次出现的状态，只与其第n-1次的状态有关，它与以前的状态无关。举一个通俗例子说：池塘里有三片荷叶和一只青蛙，假设青蛙只在荷叶上跳来跳去。若现在青蛙在荷叶Ａ上，那么下一时刻青蛙要么在原荷叶Ａ上跳动，要么跳到荷叶Ｂ上，或荷叶Ｃ上。青蛙究竟处在何种状态上，只与当前状态有关，而与以前位于哪一片荷叶上并无关系。这种性质，就是无后效性。

　　所谓“无后效性”，是指过去对未来无后效，而不是指现在对未来无后效。马尔可夫链是与马尔可夫过程紧密相关的一个概念。马尔可夫链指出事物系统的状态由过去转变到现在，再由现在转变到将来，一环接一环像一根链条，而作为马尔可夫链的动态系统将来是什么状态，取什么值，只与现在的状态、取值有关，而与它以前的状态、取值无关。因此，运用马尔可夫链只需要最近或现在的动态资料便可预测将来。马尔可夫预测法就是应用马尔可夫链来预测市场未来变化状态。

转移概率和转移概率矩阵

　　（一）转移概率

　　运用马尔可夫预测法，离不开转移概率和转移概率的矩阵。事物状态的转变也就是事物状态的转移。事物状态的转移是随机的。例如，本月份企业产品是畅销的，下个月产品是继续畅销，或是滞销，是企业无法确定的，是随机的。由于事物状态转移是随机的，因此，必须用概率来描述事物状态转移的可能性大小。这就是转移概率。转移概率用“ ”表示。下面举一例子说明什么是转移概率。

　　（二）转移概率矩阵

　　所谓矩阵，是指许多个数组成的一个数表。每个数称为矩阵的元素。矩阵的表示方法是用括号将矩阵中的元素括起来，以表示它是一个整体。如Ａ就是一个矩阵。

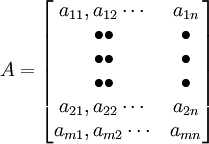
　　 $A=\begin{bmatrix} a_{11},a_{12}\cdots & a_{1n} \\ \bullet \bullet & \bullet \\ \bullet \bullet & \bullet\\ \bullet \bullet & \bullet\\ a_{21},a_{22}\cdots & a_{2n}\\ a_{m1},a_{m2}\cdots & a_{mn}\end{bmatrix}$

　　这是一个由m行n列的数构成的矩阵，表示位于矩阵中第i行与第j列交叉点上的元素，矩阵中的行数与列数可以相等，也可以不等。当它们相等时，矩阵就是一个方阵。

　　由转移概率组成的矩阵就是转移概率矩阵。也就是说构成转移概率矩阵的元素是一个个的转移概率。

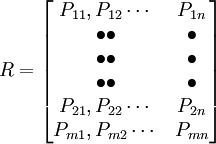　　 $R=\begin{bmatrix} P_{11},P_{12}\cdots & P_{1n} \\ \bullet \bullet & \bullet \\ \bullet \bullet & \bullet\\ \bullet \bullet & \bullet\\ P_{21},P_{22}\cdots & P_{2n}\\ P_{m1},P_{m2}\cdots & P_{mn}\end{bmatrix}$ 　　　（9-11）

　　转移概率矩阵有以下特征：

　　①,0≤Pij≤1

　　②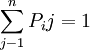 $\sum^{n}_{j-1}P_i j=1$ ，即矩阵中每一行转移概率之和等于1。

马尔可夫预测法案例分析

案例一:马尔可夫预测法进行某企业经营状况预测

　　用马尔可夫预测法预测企业经营状况的关键步骤有两步：

　　(1)由企业过去的经营状况确定一步转移概率矩阵；

　　(2)求出n步转移概率矩阵，完成n个时段后企业经营状况的预测。

　　其中步骤(1)又可分为两步，首先要确定各时段的企业经营状况，其次是根据其状态转移规律确定一步转移概率矩阵中各元素的值。

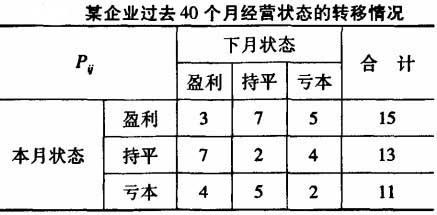
　　假设某企业的经营状况分为盈利、持平、亏本3种状态，分别记为E1、E2、E3。该企业在过去40个月即2004年1月至2007年4月的经营状况变化情况如表所示。

　　从表中可见，在15个从El出发的状态中，有3个转移到了El，7个转移到了E2，5个转移到了E3。相应得出从E2和E3出发的状态的转移情况。总的状态转移情况如表所示。

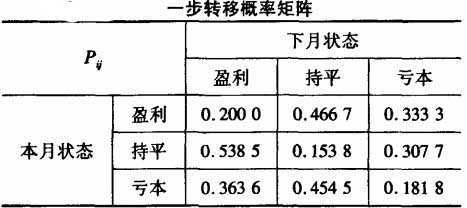
　　其中行方向上的“盈利、持平、亏本”表示出发的状态，列方向上的“盈利、持平、亏本”表示一步转移到的状态。“合计”列表示从“盈利”、“持平”、“亏本”状出发的总的次数。接下来以频率近似代替概率，便可得到其一步转移概率矩阵，如下表所示。其中概率值可用Excel的公式计算完成。其数学公式如：从盈利到盈利的一步转移概率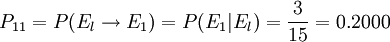 $P_{11}=P(E_l\to E_1)=P(E_1|E_l)=\frac{3}{15}=0.2000$ ；从持平到亏本的一步转移概率 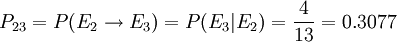$P_{23}=P(E_2\to E_3)=P(E_3|E_2)=\frac{4}{13}=0.3077$ ，其余可相应得出。

案例二:马尔可夫预测法的应用

　　一、对市场占有率的预测

　　在市场经济的条件下，各企业都十分注意扩大自己的市场占有率。因此，预测企业产品的市场占有率，就成为企业十分关心的问题。

　　若假设：

　　①市场的发展变化只与当前市场条件有关；

　　②没有新的竞争者加入，也没有老的竞争者退出；

　　③顾客总量保持不变；

　　④顾客在不同品牌之间流动的概率保持不变，就可用马尔可夫预测法对市场占有率进行预测。

　　当然，假设与市场实际存在差距，只要预测对象基本符合假设条件，就可以运用此法得出相对科学的预测结论。

　　根据马尔可夫链的基本原理，一般情况下，本期市场占有率仅取决于上期市场占有率和转移概率。因此要预测Ｋ月后的市场占有率，其矩阵为ABk 。

　　二、对市场占有率的预测马尔可夫预测法的一般步骤

　　1.调查目前本企业产品市场占有率状况,得到市场占有率向量A

　　由于市场上生产与本氽业产品相同的同类企业有许多家，但我们最关心的是本企业产品的市场占有率。故一般情况下，可以运用问卷形式进行抽样凋查，得出与本企业有关的同类产品目前在市场上占有率向量A=P1、P2、P3……Pn),1、2、3、……n代表又n家同类企业,且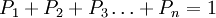 $P_1+P_2+P_3\ldots+P_n=1$ 或100%。

　　2.调查消费者的变动情况，计算转移概率矩阵B

　　对于众多的消费者而言，购不购买本企业的产品纯粹是偶然事件，但是若本企业生产的产品在质量、价格、营销策略相对较为稳定的情况下，众多消费者的偶然的购买变动，就会演变成必然的目前该类产品相对稳定的市场变动情况。

　　因为原来购买本企业产品的消费者在将来可能仍然购买奉企业的产品，也可能转移到购买别的企业的同类产品，而原来购买其他企业产品的消费者，在将来可能会转移到购买本企产品，两者互相抵消，就能形成相对稳定的转移概率，只要通过市场调查，就能得到购买本企业和其他企业产品的转移概率矩阵。

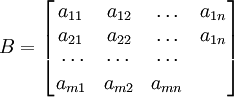
　　 $B=\begin{bmatrix}a_{11}&a_{12}&\ldots&a_{1n}\\a_{21}&a_{22}&\ldots&a_{1n}\\\ \cdots&\cdots&\cdots\\a_{m1}&a_{m2}&a_{mn}\end{bmatrix}$

　　矩阵B称为转移概率矩阵，且要求矩阵的各行元素之和为1，即购买某种产品的消费者中，将来购买本企业产品和购买非本企业产品的消费者人数的比重之和等于1或100%。

　　3.用向量A和转移概率矩阵B预测下一期本企业产品市场占有率。

　　若已知某产品目前市场占有率向量A，又根据凋查结果得到未来转移概率矩阵B，则未来某产品各企业的市场占有率可以用A乘以B求得。

　　即A×B=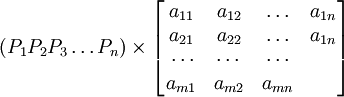 $(P_1P_2P_3\ldots P_n)\times\begin{bmatrix}a_{11}&a_{12}&\ldots&a_{1n}\\a_{21}&a_{22}&\ldots&a_{1n}\\\ \cdots&\cdots&\cdots\\a_{m1}&a_{m2}&a_{mn}\end{bmatrix}$

　　三、产品长期市场占有率预测的实证分析

　　现以某市某品牌彩电市场占有率预测为例说明马尔可夫预测法在实际市场占有率顶测中的应用。

　　就全球而言，生产彩电的企业成下上万，但我们最为关心的足本企业品牌彩电的市场占有率情况，为了在市场竞争中做到知己知彼，我们当然需要掌握其他彩电的市场占有情况．但成千上万种彩电的市场占有情况我们不可能电不必要统统调查，只要调杏在彩电牛产企业中市场占有率最大，竞争嫩里最强，对本公司产品构成威胁的龙头企业产品占有率情况，而把大量的其他彩电生产企业产品对如其他类，这样，就能把成千上万中彩电归纳为三大企业:即本企业、龙头企业、其他企业。根据马可夫预测法的预测步骤，

　　第一步，要调查目前市场的占有率情况，得到市场占有率向量A，若通过对本市一万户彩电用户的随机调查，得出目前市场占有率向量A=(0.2、0.5、0.3)即目前，在一万户用户中，购买本企业彩电户数占20%，购买龙头企业品牌彩电用户数占50%，还有30%是购买其他品牌彩电。

　　第二步，调查消费购买变动情况，得出整个市场彩电下一期的转移概率矩阵B，若经过调查，这一万户消费者，下一期若购买彩电，在现在购买本企业彩电的消费者中，下一期仍然有50%购买本企业彩电，40%将购买龙头企业的彩电，10%将购买其他牌号的彩电；现在购买龙头企业彩电的消费者，下一期将有20%转移购买我公司的生产的彩电；50%仍然购买龙头企业彩电，而30%将购买其他牌号的彩电；现在购买其他品牌彩电，而有40%将转移购买龙头企业产品30%将购买本企业的彩电。据此可得出下期整个市场彩电购买情况变动的转移概率矩阵。

　　 $\begin{bmatrix}0.5&0.4&0.1\\0.2&0.5&0.3\\0.3&0.4&0.3\end{bmatrix}$

　　第三步，用向量S乘以矩阵B即可得出下期本企业、龙头企业及其他企业市场占有率分别为29％、45％和26％，第四步,若这种变化成为相对稳定状况，也即转移概率矩阵将对市场占有率不起变动作用，我们就可以计舒：出竞争相对稳定以后的王种牌号彩电的市场占有率。设x = (x1x2X3)是稳定以后的市场占有率，则x不随时间的推移而变化，也即市场占有率处于动态平衡，即有xB=x，详细写出来即为

　　即(x1x2X3)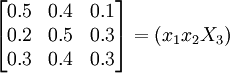 $\begin{bmatrix}0.5&0.4&0.1\\0.2&0.5&0.3\\0.3&0.4&0.3\end{bmatrix}=(x_1x_2X_3)$

　　可以联立方程组：

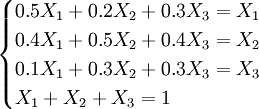
　　 $\begin{cases}0.5X_1+0.2X_2+0.3X_3=X_1\\0.4X_1+0.5X_2+0.4X_3=X_2\\0.1X_1+0.3X_2+0.3X_3=X_3\\X_1+X_2+X_3=1\end{cases}$

　　解方程组得x1 = 32.92,x2 = 36.36,x3 = 30.69，本企业产品在市场较为稳定情况下的市场占有率为32.92％，龙头企业为36.36％，其他企业为30.69％。

　　四、对使用马尔可夫预测法的总结

　　马尔可夫预测法是一种既实用叉较为方便的市场占有率预测方法+运用马尔可夫预测法关键是要调查得到企业目前市场占有率情况，以及下期市场占有牢的改变方向，而要得到这些资料，必须进行抽样渊查，在抽样调查时，需要注意样本的代表件，牢牢遵循抽样调查的随机原则，否则就得水到准确的预测结果。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家小花儿/article/detail/380338

【机器学习】马尔可夫（Markov）预测法 整理_马尔科夫预测能解决哪些类型的问题