72.Minimum Falling Path Sum(下降路径最小和)
题目:
给定一个方形整数数组 A,我们想要得到通过 A 的下降路径的最小和。
下降路径可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列。
示例:
输入:[[1,2,3],[4,5,6],[7,8,9]] 输出:12 解释: 可能的下降路径有:
-
[1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9][2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9][3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]
和最小的下降路径是 [1,4,7],所以答案是 12。
思路:
从第二行开始,上方下落路径至多三条,左上,上,右上,如果是两侧只有两条路径。直接在上方数字中找到最小数值,加上本身数值,这就是到达该点的和最小的下降路径。
接下来一行一行向下,直到计算到最后一行,遍历最后一行,找到最小值即可。
图解:
红色是计算式,左上角是本来数组的值。
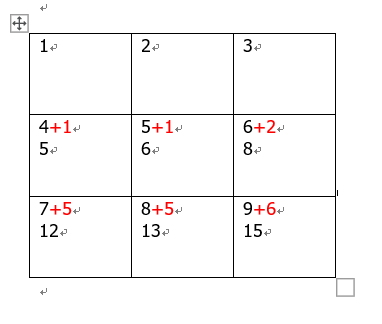
代码:


1 public static int minFallingPathSum(int[][] A) { 2 int min = 9999; 3 int len = A.length; 4 for(int i = 1;i<len;i++) 5 { 6 for(int j = 0;j<len;j++) 7 { 8 if(j==0) 9 { 10 A[i][j] = A[i][j] + Math.min(A[i-1][j], A[i-1][j+1]); 11 } 12 else if(j==len-1) 13 { 14 A[i][j] = A[i][j] + Math.min(A[i-1][j], A[i-1][j-1]); 15 } 16 else 17 { 18 A[i][j] = A[i][j] + Math.min(A[i-1][j], Math.min(A[i-1][j-1], A[i-1][j+1])); 19 } 20 } 21 } 22 for(int i = 0;i<len;i++) 23 { 24 if(min>A[len-1][i]) 25 min = A[len-1][i]; 26 } 27 return min; 28 }


