【笔试】4399_4399编程题硬币

自己总结，答案不一定对，代码也没验证

单选

1

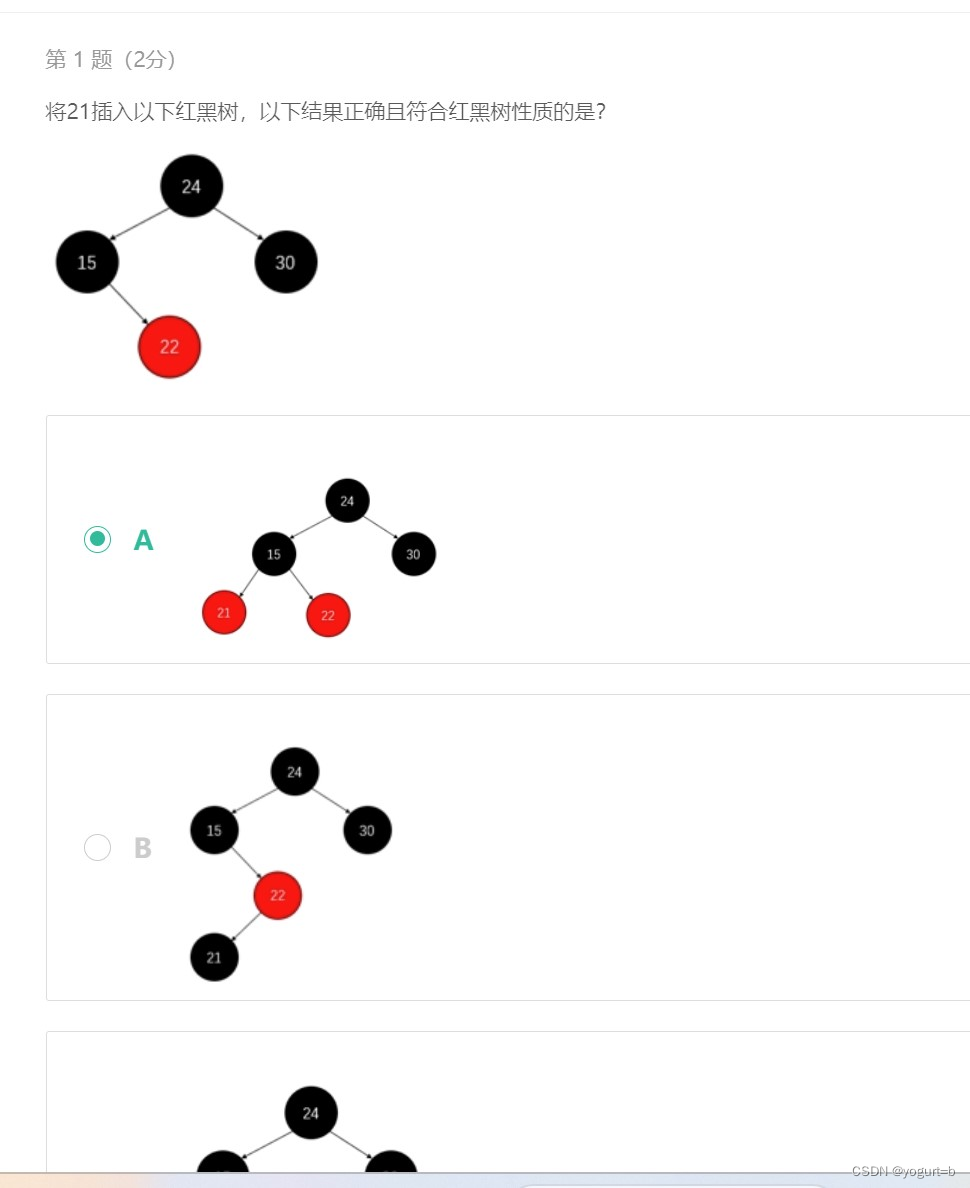在红黑树中，具有以下性质：
每个节点要么是红色，要么是黑色。
根节点是黑色的。
每个叶子节点（NIL 节点）都是黑色的。
如果一个节点是红色的，那么它的子节点必须是黑色的。
从任何给定节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点，这被称为"黑高度"。

插入新节点：
首先，将新节点插入到红黑树中，就像插入普通的二叉搜索树一样，保持二叉搜索树的性质。
设置新节点颜色：
新插入的节点通常被标记为红色。这是因为在插入后，树的性质可能会被破坏，标记为红色有助于后续的修复。
修复红黑树性质：
插入节点后，需要检查红黑树的性质是否被破坏，如果被破坏，需要进行一系列旋转和颜色调整操作来修复它。

2

假设由客户端主动断开连接，以下关于tcp状态转移的描述中，错误的一项是
A客户端发送FIN报文后立即进入FIN WAIT 1状态
客户端给服务端返回确认报文后立即进入CLOSED状态
服务端收到客户端的确认报文后立即进入CLOSED状态
服务端给客户端返回确认报文后进入CLOSE WAIT状态

TCP关闭流程

客户端收到确认报文：

客户端收到服务端的确认报文后，进入FIN WAIT 2状态，表示客户端已经完成发送和接收数据，并等待服务端的关闭请求。
服务端决定关闭连接：

当服务端也准备关闭连接时，它发送一个带有FIN标志的TCP报文给客户端。
客户端收到服务端的FIN报文：

客户端收到服务端发送的带有FIN标志的报文后，发送一个确认报文，然后进入TIME WAIT状态，等待可能丢失的确认报文，以确保数据完整性。
服务端收到确认报文：

服务端收到客户端的确认报文后，进入CLOSED状态，表示连接已经关闭。
客户端结束TIME WAIT状态：

客户端在TIME WAIT状态等待一段时间后，进入CLOSED状态。

3

下面关于MySQL中的锁机制说法错误的是
A MySQL中的锁主要用于解决多个线程并发访问某一资源导致的数据不一致问题
B 不同存储引擎支持的锁机制不同，MyISAM采用的是表级锁，而lnnodb支持行级和表级锁B
C MyISAM支持共享读锁与独占写锁，即可理解为两个不同线程对MyISAM表进行读写操作和写写操作时，都是串行执行送
D Innodb支持共享锁(s)和排它锁(x)，排它锁即为一个事务对某行数据加了排它锁时，其他事务可读但不可写该行的最新数据

MySQL中的锁机制

C这句话描述是不准确的。MyISAM表在读操作和写操作之间是串行执行的，但不是因为共享读锁和独占写锁。实际上，MyISAM表使用的是表级锁，这意味着只有在没有其他事务锁定整个表的情况下，才能进行写操作。读操作可以并行进行，不会被写操作阻塞，但写操作会阻塞其他的写操作和读操作，因此并不是真正的支持共享读锁和独占写锁。

编程

2

给你一个整数数组coins,表示不同面额的硬币，以及一个整数amount，表示总金额计算并返回可以凑成总金额所需的 最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回-1。你可以认为每种硬币的数量是无限的。
要求:时间复杂度O(Sn)S是金额，n是面额数
数值范围:
1 <= coins.length <= 12
0 <= amount <= 10^4
[测试用例]
输入: coins =[1,2,5], amount = 11
输出:3
输入: coins =[2],amount =3
输出:-1
输入: coins =[1],amount =0
输出:0

动态规划

#include <iostream>
#include <vector>
using namespace std;

int coinChange(vector <int>& coins,int amount){
	vector<int> dp(amount+1,amount+1);
	dp[0]=0;
	for(auto coin:coins)
	{
		for(int i=coin;i<=amount;i++)
		{
			dp[i]=min(1+dp[i-coin],dp[i]);
		}
	 } 
	return dp[amount] == amount+1? -1 : dp[amount];
}
int main() 
{
	int n;
	cin>>n;
	vector<int> coin;
	int tmp;
	while(n--)
	{
		cin>>tmp;
		coin.push_back(tmp);
	}
	int amo;
	cin>>amo;
	int res = coinChange(coin,amo);
	cout<<res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

编程3

你参与了一个微信小游戏的研发，策划同学计划给你发布n项任务，每项任务会有一个 发布时间点r和 预估处理时长p ，你需要等待任务发布后才能开始编码实现，同时每项任务都会有一位测试同学跟进测试工作，你需要合理安排工作，让所有测试同学等待的时间之和最少，此外你作为一个资深的程序员，多项任务可以交替进行输入:nr1p1…rn pn
输出:各项任务的任务id和完成时间，任务id从下标1开始，按完成时间升序排列比如
输入:2 1 4 3 1
即发布2项任务，任务1的发布时间点r=1，处理时长p=4;任务2的发布时间点r=3，处理时长p=1，合理的工作安排如下图所示
输出:
2 4
1 6
测试同学等待的总时长为10

在某个时间点剩余执行时间越短越优先

STCF 最短完成时间优先
GPT给出的算法：

#include <iostream>
#include <vector>

using namespace std;

struct Process {
    int id;          // 进程ID
    int arrivalTime; // 到达时间
    int burstTime;   // 执行时间
    int completionTime; // 完成时间
};

// 按到达时间升序排序进程
bool compareArrivalTime(const Process& p1, const Process& p2) {
    return p1.arrivalTime < p2.arrivalTime;
}

int main() {
    int n; // 进程数量
    cout << "请输入进程数量: ";
    cin >> n;

    vector<Process> processes(n);

    // 输入进程信息
    for (int i = 0; i < n; i++) {
        processes[i].id = i + 1;
        cout << "进程 " << processes[i].id << " 的到达时间: ";
        cin >> processes[i].arrivalTime;
        cout << "进程 " << processes[i].id << " 的执行时间: ";
        cin >> processes[i].burstTime;
    }

    // 按到达时间升序排序进程
    sort(processes.begin(), processes.end(), compareArrivalTime);

    int currentTime = 0; // 当前时间
    int totalCompletionTime = 0; // 所有进程的总完成时间

    // STCF算法
    while (!processes.empty()) {
        int shortestJobIndex = -1;
        int shortestJobTime = INT_MAX;
//可以先对process按到达时间排序
        for (int i = 0; i < processes.size(); i++) {
            if (processes[i].arrivalTime <= currentTime && processes[i].burstTime < shortestJobTime) {
                shortestJobIndex = i;
                shortestJobTime = processes[i].burstTime;
            }
        }
//这一块没体现抢占，应该修改为按一个一个世界片或者执行到下一个进程到达时间，而不是全部做完
        if (shortestJobIndex == -1) {
            currentTime++;
        } else {
            Process& currentProcess = processes[shortestJobIndex];
            currentProcess.completionTime = currentTime + currentProcess.burstTime;
            totalCompletionTime += currentProcess.completionTime;
            currentTime += currentProcess.burstTime;
            processes.erase(processes.begin() + shortestJobIndex);
        }
    }

    // 计算平均完成时间
    double averageCompletionTime = static_cast<double>(totalCompletionTime) / n;
    cout << "平均完成时间: " << averageCompletionTime << endl;

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69