【论文阅读】互连网络的负载平衡路由算法 (GAL, Globally Adaptive Load-balancing 全局自适应负载平衡)

• Globally Adaptive Load-balancing 全局自适应负载平衡
  • GAL: Globally Adaptive Load-balanced routing 全局自适应负载平衡路由
    • 1. GAL on a ring
    • 2. GAL on higher dimensional torus
    • 3. 实验性能
    • 4. 算法稳定性 Stability
    • 总结
  • References

Globally Adaptive Load-balancing 全局自适应负载平衡

将自适应(adaptive)引入后，可以发现自适应算法比 oblivious 算法具有更优越的平均性能。但最坏情况下(worst-case)的高吞吐量的代价是本地流量(local traffic)的下降，对于任何类型的不经意的错误路由(绕远)来说，良性流量的次优性能仍然亟待解决。

此次重点讨论自适应算法，引入了两种新的全局自适应负载均衡路由方法，称为 GAL[1] 和 CQR[2]。与之前基于本地信息(具有最短输出队列(shortest output queue)的有效维度)做出路由决策的自适应路由算法不同，全局自适应负载均衡算法使用分段注入队列(segmented injection queues)或通道队列(channel queues)来感知全局拥塞，以决定每个维度的路由方向。它们通过自适应地在选定的方向上进行路由来进一步平衡网络的负载。使用近似全局信息使 GAL 和 CQR 能够在良性流量模式上实现最小自适应路由的性能(延迟和吞吐量)，同时在对抗性流量上实现明显的负载平衡目标。

GAL: Globally Adaptive Load-balanced routing 全局自适应负载平衡路由

迄今为止讨论(在当时)的自适应算法还没有在良性模式(benigh patterns)(例如 UR、NN)和对抗模式（例如 TOR）上都产生最佳吞吐量。理想的算法会以最小路由路由良性流量，并在网络通道上平衡对抗性流量的负载。在本节中，我们提出一种路由算法 GAL，该算法使用近似全局信息(approximate global infomation)，将其路由决策在合适的时刻从最小更改为非最小。首先考虑在节点环上路由良性流量 NN 和对抗性流量 TOR 的算法，然后将 GAL 扩展到更高维的环面网络。

1. GAL on a ring

为了感知 8 节点的 ring 的近似全局信息，需要考虑每个源节点的 8 组注入队列(即将注入队列分段)，每个组对应一个目标节点。每个组包含两个队列，一个最小队列和一个非最小队列(高维便是多个非最小队列)。当从终端节点接受数据包时，如果该队列的长度(已存储数据包/flit的个数)小于阈值T(threshold)，则将数据包放在目的地组中的最小队列进行最小路由，否则将其插入到两个队列中较短的队列中，如图5.1所示。

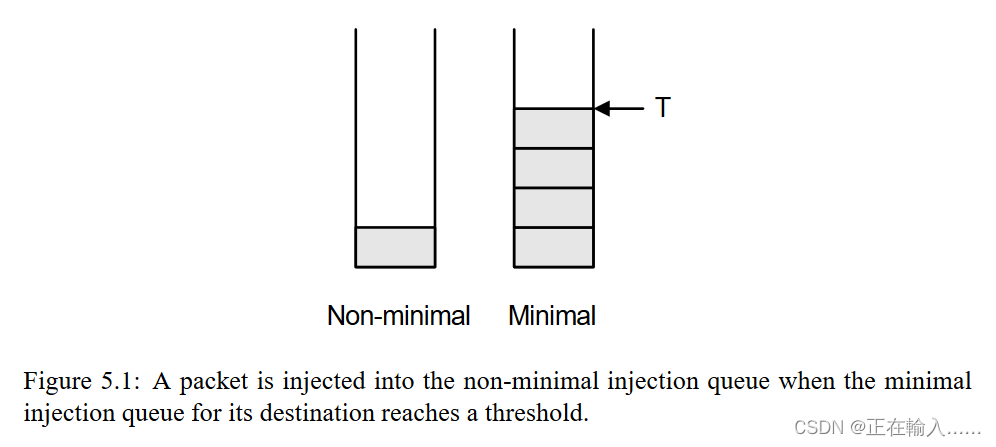
当使用这种方案时，理想情况是 NN 流量模式总是被最小化，即永远不会到达最小队列的阈值。而当用此方案去路由 TOR 流量模式时，最初所有的数据包都会使用最小路由，然而当达到 0.33 load 的负载，最小方向会达到饱和而阈值也会被超过，因此方案接下来会将以非最小路由的方式发送剩下的数据包。

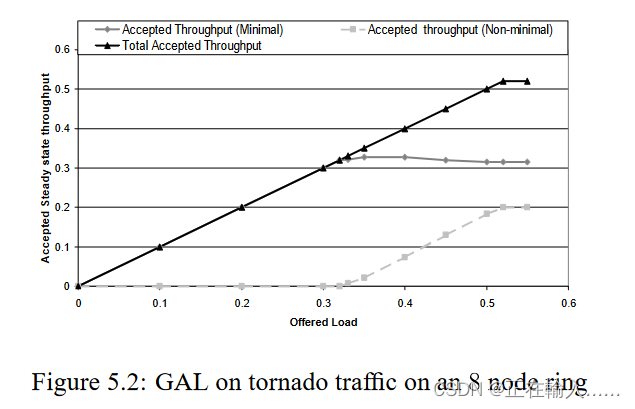
如图5.2所示，方案在低负载时以最小路由进行路由，只有当最小通道在 0.33 的负载下饱和后，最小队列长度才会超过阈值。此时一些流量会被非最小路由。随着负载的增加，更多的流量会被非最小路由。在饱和时，负载会以5/8的流量最小路由和3/8的流量非最小路由比例保持平衡。因此通过使用近似全局拥塞信息做出全局路由决策(最小或非最小)，该方案能够在良性模式(NN)和对抗模式(TOR)上实现最佳性能，这是先前路由算法没有实现的。

2. GAL on higher dimensional torus

将 GAL 引入高维度 Torus 拓扑。在 n 个维度的 torus 拓扑中，将源节点 s 到目标节点 d 的所有可能路径划分为 2^n 个象限(quadrants)，每个象限对应一种方向组合(每个维度提供一个方向)。GAL为每个象限提供一组单独的注入队列。图5.3显示了2-D network的每个节点的设置。

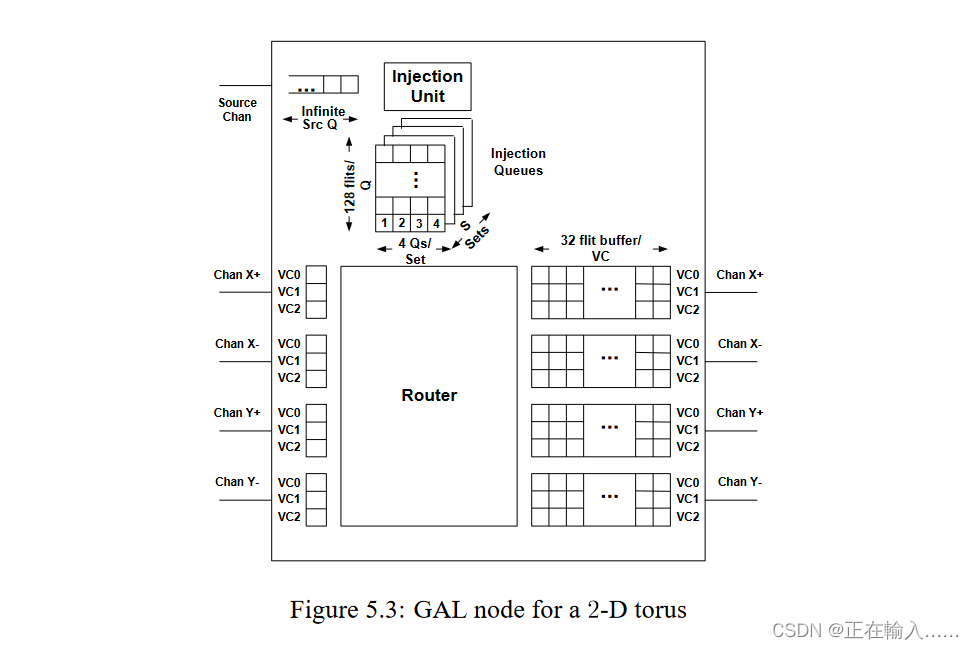
每个 node(路由器)都有一个无限源队列对终端节点的网络接口进行建模，类似于 Booksim 模拟器模拟中的注入队列。每个节点中共有 S = k^2 个组(Sets)，每个组包含4个注入队列(代表四个象限，其中一个为最小路由队列，根据源目标节点对)。当注入单元(injection unit)接收数据包时，注入Sets由目标节点确定。当确定了注入组后，在组中，选择注入队列(即选择象限)按如下步骤：

• 优先选择与从源到目标节点拥有最小距离且其占用率小于阈值的相关的象限的队列。如果队列超过了阈值，则选择所有队列中最短的队列。
• 一旦选择了象限，数据包就会在该象限内进行自适应路由，如 GOAL 按照本地拥塞信息(具有最短队列的有效维度)进行自适应路由。

如图5.3所示，GAL 路由算法需要和 GOAL 一样的 3 个 VC 通道在每个单向的物理通道去保证无死锁。一旦为数据包选择了象限，数据包就会在该象限中单调地前进，从而无活锁。

3. 实验性能

将 GAL 与自适应算法 CHAOS、MIN AD 和 GOAL 的性能进行比较。图 5.3 显示了 GAL 节点的实验设置。每个节点都有一个无限源队列来对网络接口进行建模，并且有 8x8 = 64 组用于 8x8 环面的注入队列。每组都有与每个象限相对应的 4 个注入队列(每个队列都有128flit deep)。路由器中每个单向的物理通道分别有 3 个 VC 通道(32 flits deep each)。假设每个数据包长度为 1 flit，以便将路由算法研究与流量控制问题分开。对于每个最小注入队列，GAL 的阈值为 2 flits。所有算法的总缓冲区资源保持恒定，即 VC 数量和 VC 通道缓冲区深度的乘积保持恒定。

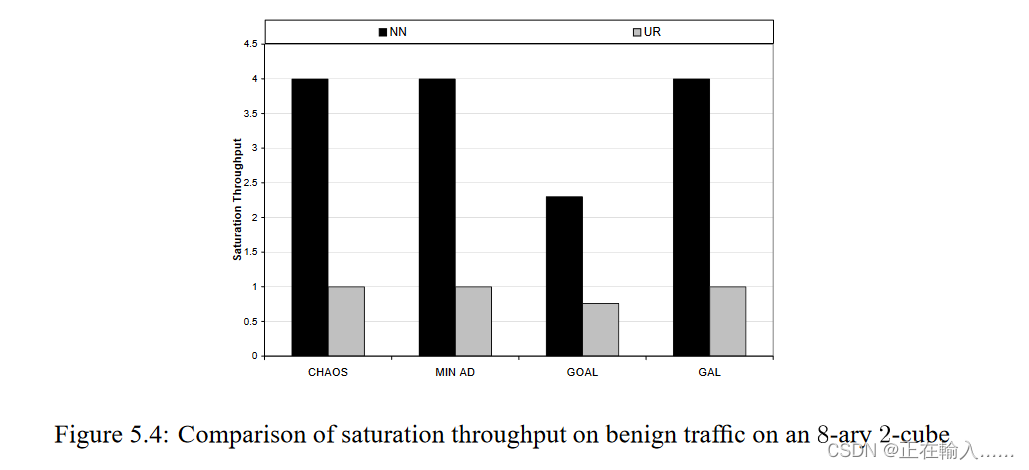
良性和对抗性流量模式的四种算法的吞吐量性能。两种良性流量模式如图 5.4 所示，而四种对抗性模式如图 5.5 所示。这些数字表明，GAL 是唯一能够在这两类流量模式上提供最佳性能的算法。它成为一种类似 GOAL 的负载均衡算法，并与对抗流量上 GOAL 的吞吐量相匹配。同时，它在良性模式上的表现并与 MIN AD 在这些模式上的性能相匹配。

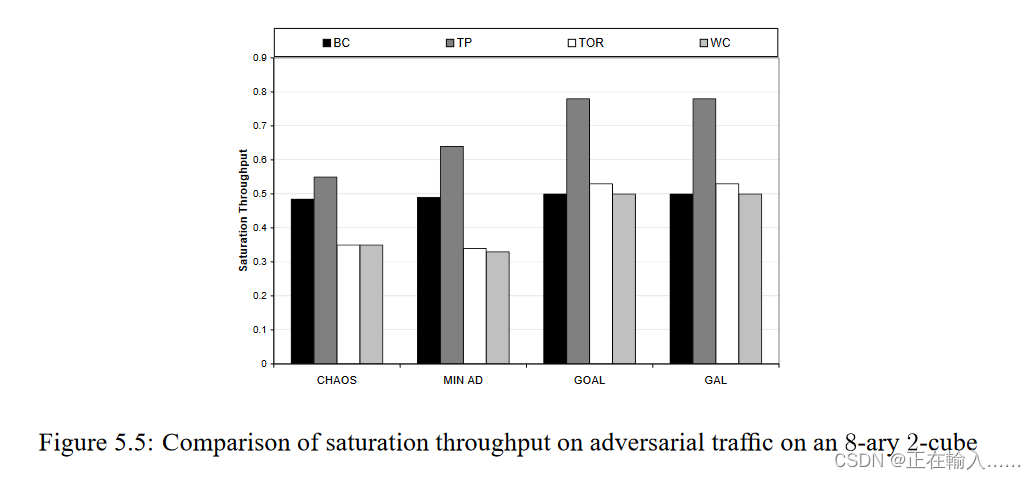
此外还有延迟等性能的比较，此处不一一总结。

4. 算法稳定性 Stability

之前讨论了路由算法稳定性的重要性。即如果提供的负载增加到超过饱和点，可接受的吞吐量仍保持恒定，则算法是稳定的。对于非最小自适应路由算法来说，实现稳定性可能具有挑战性，因为很难区分负载不平衡引起的拥塞和负载平衡网络饱和引起的拥塞。在前一种情况下，重新路由流量(可能是非最小流量)可以缓解这种不平衡并增加吞吐量。然而，在负载平衡但饱和的情况下，重新路由流量可能会导致不平衡并降低吞吐量。 GAL 通过测量吞吐量的变化并调整其队列阈值来解决这种不稳定问题。更改这些阈值可以控制非最小发送的数据包比例，这反过来又用于保持稳定性。

一个简单的示例来演示控制非最小发送数据包比例的必要性。考虑使用 GAL 路由 UR 流量但使用固定队列阈值的情况。对于超出饱和的提供的负载，流量最初将被最小化路由，因为最小队列是空的(应该是没有到达阈值)。由于网络无法承受所有流量，背压将导致数据包传输到到最小队列中。尽管最小路由完美地平衡了 UR 流量的负载，但这些队列的占用率最终将超过固定阈值，并且某些流量将被非最小路由。此时，吞吐量将开始下降，因为通道带宽被非最小数据包浪费(图 5.10)。

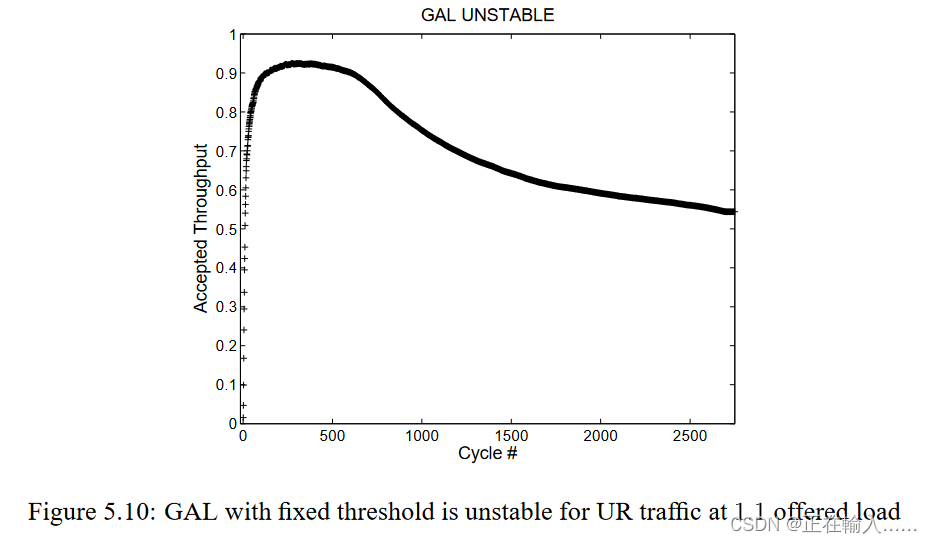
相反，如果数据包没有进行非最小路由，吞吐量将保持稳定。为了控制非最小路由的数据包数量，GAL 在队列深度设置的最小值Tmin和最大值Tmax之间动态改变每个阈值 T。这是针对每个队列集(queue set，即针对每一个目标节点进行动态调整)独立完成的。然后，阈值限制非最小路由的数据包的比例 - 增加会降低数据包被放置在非最小队列中的可能性，并且当 T = Tmax 时，所有数据包都被最小路由。 为了确保稳定性，只要观察到吞吐量下降，T就会增加。如果一直下降，T会持续增加到Tmax为止。流量模式可能之后会进行变化，使得非最小路由重新有效，当吞吐量不变或者增加，T就会下降。

文章通过检测每个源节点对应集合中的所有注入队列在一个周期内排出的数据包的总数来估算每个源-目标节点对的吞吐量。这也是针对每个队列集(queue set，即针对每一个目标节点进行动态调整)独立完成的。

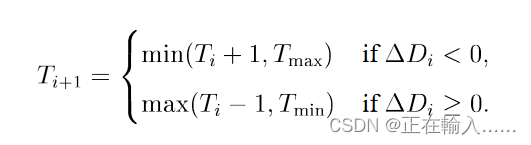
图 5.11 显示了阈值调整的示例。测试设置如下：在 1.10 注入负载下施加 UR 流量，然后在第 600 个周期切换到注入负载下的 TOR。因此，具有阈值调整方案的 GAL 对于良性和硬性流量模式都是稳定的。但是在阈值进行调整的过程中，以及通过阈值进行最小非最小路由切换所带来的延迟较高，后续需要解决。

总结

在低负载和良性流量模式下，GAL 最小限度地路由所有流量，因此与此类友好流量上的最小路由算法的低延迟和高吞吐量相匹配。在对抗性流量模式下，GAL 在低负载时进行最小路由，然后在注入队列检测到拥塞时切换到非最小路由。在饱和状态下，GAL 与最佳负载平衡的不经意路由的吞吐量相匹配。这结合了最小算法（低负载下的低延迟）和明显负载平衡算法（高饱和​​吞吐量）的最佳功能。

虽然 GAL 在各种吞吐量和延迟指标上比任何其他已知的路由算法表现更好，但 GAL 存在四个严重问题：

• 一旦开始非最小路由流量，它就会具有非常高的延迟。
• 适应流量变化较慢。
• 需要复杂的方法来实现稳定性。
• 算法实施起来很复杂。

这些问题都与 GAL 使用注入队列长度来推断全局拥塞有关。之后将介绍通道队列路由(CQR - 发音为“seeker”)[2]，它与 GAL 在本地和困难模式上实现高吞吐量的能力相匹配，但克服了 GAL 的局限性。 CQR 通过使用通道队列而不是注入队列来估计全局拥塞，从而克服了这些限制。在需要非最小路由的负载下，CQR 的延迟比 GAL 低得多。它能够快速适应流量的变化，无条件稳定，并且实现简单。

References

[1] A. Singh, W. J. Dally, A. K. Gupta, and B. Towles, “Adaptive channel queue routing on k-ary n-cubes,” in Proceedings of the sixteenth annual ACM symposium on Parallelism in algorithms and architectures, Barcelona Spain: ACM, Jun. 2004, pp. 11–19. doi: 10.1145/1007912.1007915.
[2] A. Singh, W. J. Dally, B. Towles, and A. K. Gupta, “Globally Adaptive Load-Balanced Routing on Tori,” IEEE Comput. Arch. Lett., vol. 3, no. 1, pp. 2–2, Jan. 2004, doi: 10.1109/L-CA.2004.8.