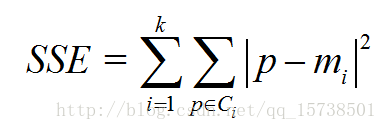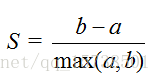devbox
我家小花儿
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

机器学习算法（7）——K近邻(KNN)、K-means、模糊c-均值聚类、DBSCAN与层次与谱聚类算法_dbscan,knn

作者：我家小花儿 | 2024-05-01 07:14:25

赞

踩

dbscan,knn

1、K-近邻算法（KNN）概述 （有监督算法，分类算法）

     最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢，其次就是存在一个测试对象同时与多个训练对象匹配，导致一个训练对象被分到了多个类的问题，基于这些问题呢，就产生了KNN。

     KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

     下面通过一个简单的例子说明一下：如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。
                                               

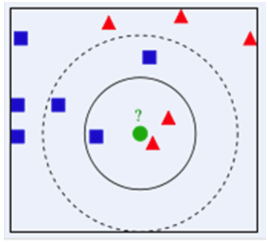
    由此也说明了KNN算法的结果很大程度取决于K的选择。

     在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离（城市街区距离(CityBlock distance)）：

                      

同时，KNN通过依据k个对象中占优的类别进行决策，而不是单一的对象类别决策。这两点就是KNN算法的优势。

      对KNN算法的思想总结一下：就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：

1）计算测试数据与各个训练数据之间的距离；

2）按照距离的递增关系进行排序；

3）选取距离最小的K个点；

4）确定前K个点所在类别的出现频率；

5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

from：http://www.cnblogs.com/ybjourney/p/4702562.html

KNN的主要优点有：

　　　　1） 理论成熟，思想简单，既可以用来做分类也可以用来做回归

　　　　2） 可用于非线性分类

　　　　3） 训练时间复杂度比支持向量机之类的算法低，仅为O(n)

　　　　4） 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感

　　　　5） 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合

　　　　6）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分

KNN的不足：

1、计算量大，分类速度慢

      改进：浓缩训练样本集 ；加快K个最近邻的搜索速度

2、KNN在对属性较多的训练样本进行分类时，由于计算量大而使其效率大大降低效果。懒惰算法，对测试样本分类时的计算量大，内存开销大，评分慢

3、K值难以确定 
· 目前没有很好的方法，一般采用先定一个初始值，然后根据实验测试的结果调整K值。 

4、对不平衡样本集比较敏感

    当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。改进：采用权值的方法（增大距离小的邻居样本的权值）

Python实现：

  1. import numpy as np
  2. Dataset=np.array([[1.0,2.0],[1.2,0.1],[0.1,1.4],[0.3,3.5]])
  3. labels=['A','A','B','B']
  4. test=[1.1,0.3]
  5. k=3
  6. #分类
  7. diff=test-Dataset
  8. squaredist=np.sum(diff**2,axis=1)
  9. dist=squaredist**0.5
  10. index=np.argsort(dist)
  11. dict={}
  12. for i in range(k):
  13.     vote=labels[index[i]]
  14.     dict[vote]=dict.get(vote,0)+1
  15. max=0
  16. for key,value in dict.items(): #以列表返回可遍历的(键, 值) 元组数组
  17.     if max<value:
  18.         max=value
  19.         classes=key
  20.  
  21. print(classes)

当axis为0时,是压缩行,即将每一列的元素相加,将矩阵压缩为一行
当axis为1时,是压缩列,即将每一行的元素相加,将矩阵压缩为一列 ;

 np.argsort(-x) #按降序排列

dict.get(key, default=None)返回指定键的值，如果值不在字典中返回默认值None。
  • key -- 字典中要查找的键。
  • default -- 如果指定键的值不存在时，返回该默认值值。

2、K-均值聚类（K-means）（无监督学习、聚类算法，随机算法）

（随机算法是指：根据初始点的选择不同，最终收敛的位置可能有差异，因此要多选几次初始值，结果取最好的那一个）

1. 聚类

     “类”指的是具有相似性的集合。聚类是指将数据集划分为若干类，使得类内之间的数据最为相似，各类之间的数据相似度差别尽可能大。聚类分析就是以相似性为基础，对数据集进行聚类划分，属于无监督学习。

2、 K-means

       k-means算法是一种简单的迭代型聚类算法，采用距离作为相似性指标，从而发现给定数据集中的K个类，且每个类的中心是根据类中所有值的均值得到，每个类用聚类中心来描述。对于给定的一个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标，聚类目标是使得各类的聚类平方和最小。

a. 最常用的无监督算法 
b. 计算距离方法：欧式距离，曼哈顿距离 
c. 应用：去除孤立点，离群点（只针对度量算法）；可以离散化 
d. 最常用归一化预处理方法 
f. k-means设置超参数k时，只需要设置最大的k值。 
g. k-means算法最终肯定会得到稳定的k个中心点，可以用EM(Expectation Maximum)算法解释 
h. k-means算法k个随机初始值怎么选？ 多选几次，比较，找出最好的那个 
i. 调优的方法：1. bi-kmeans 方法（依次“补刀”） 
j. 调优的方法：2. 层次聚类（逐步聚拢法）k=5 找到5个中心点，把中心点喂给k-means。初始中心点不同，收敛的结果也可能不一致。 
k. 聚类效果怎么判断？用SSE误差平方和指标判断，SSE越小越好，也就是肘部法则的拐点处。也可以用轮廓系数法判断，值越大，表示聚类效果越好，簇与簇之间距离越远越好，簇内越紧越好。 
l. k-means算法最大弱点：只能处理球形的簇（理论） 

 3、算法流程

  K-means是一个反复迭代的过程，算法分为四个步骤：

1） 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；

2） 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；

3） 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；

4） 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）。

用以下例子加以说明：

   

      图1：给定一个数据集；图2：根据K = 5初始化聚类中心，保证　聚类中心处于数据空间内；图3：根据计算类内对象和聚类中心之间的相似度指标，将数据进行划分；图4：将类内之间数据的均值作为聚类中心，更新聚类中心。最后判断算法结束与否即可，目的是为了保证算法的收敛。

from：https://www.cnblogs.com/ybjourney/p/4714870.html

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. # coding=utf-8
  4. from numpy import *
  5. # 加载数据
  6. def loadDataSet(fileName):  # 解析文件，按tab分割字段，得到一个浮点数字类型的矩阵
  7.     dataMat = []              # 文件的最后一个字段是类别标签
  8.     fr = open(fileName)
  9.     for line in fr.readlines():
  10.         curLine = line.strip().split('\t')
  11.         fltLine = map(float, curLine)    # 将每个元素转成float类型
  12.         dataMat.append(fltLine)
  13.     return dataMat
  14.  
  15. # 计算欧几里得距离
  16. def distEclud(vecA, vecB):
  17.     return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离
  18.  
  19. # 构建聚簇中心，取k个(此例中为4)随机质心
  20. def randCent(dataSet, k):
  21.     n = shape(dataSet)[1]
  22.     centroids = mat(zeros((k,n)))   # 每个质心有n个坐标值，总共要k个质心
  23.     for j in range(n):
  24.         minJ = min(dataSet[:,j])
  25.         maxJ = max(dataSet[:,j])
  26.         rangeJ = float(maxJ - minJ)
  27.         centroids[:,j] = minJ + rangeJ * random.rand(k, 1)
  28.     return centroids
  29.  
  30. # k-means 聚类算法
  31. def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
  32.     m = shape(dataSet)[0]
  33.     clusterAssment = mat(zeros((m,2)))    # 用于存放该样本属于哪类及质心距离
  34.     # clusterAssment第一列存放该数据所属的中心点，第二列是该数据到中心点的距离
  35.     centroids = createCent(dataSet, k)
  36.     clusterChanged = True   # 用来判断聚类是否已经收敛
  37.     while clusterChanged:
  38.         clusterChanged = False;
  39.         for i in range(m):  # 把每一个数据点划分到离它最近的中心点
  40.             minDist = inf;#无穷大
  41.             minIndex = -1;
  42.             for j in range(k):
  43.                 distJI = distMeans(centroids[j,:], dataSet[i,:])
  44.                 if distJI < minDist:
  45.                     minDist = distJI;
  46.                     minIndex = j  # 如果第i个数据点到第j个中心点更近，则将i归属为j
  47.             if clusterAssment[i,0] != minIndex: clusterChanged = True;  # 如果分配发生变化，则需要继续迭代
  48.             clusterAssment[i,:] = minIndex,minDist**2   # 并将第i个数据点的分配情况存入字典
  49.         print(centroids)
  50.         for cent in range(k):   # 重新计算中心点
  51.             ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]]   # 取clusterAssment第一列等于cent的所有列
  52.             centroids[cent,:] = mean(ptsInClust, axis = 0)  # 算出这些数据的中心点
  53.     return centroids, clusterAssment
  54. # --------------------测试----------------------------------------------------
  55. # 用测试数据及测试kmeans算法
  56. datMat = mat(loadDataSet('testSet.txt'))
  57. myCentroids,clustAssing = kMeans(datMat,4)
  58. print(myCentroids)
  59. print (clustAssing)

                     

       nonzero()函数是numpy中用于得到数组array中非零元素的位置（数组索引）的函数,对于一维数组，它的返回值是一个长度为a.ndim(数组a的轴数)的元组，元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。对于二维数组b2，得到的是一个长度为2的元组。它的第0个元素是数组a中值不为0的元素的第0轴的下标，第1个元素则是第1轴的下标，

cluster[:,0].A 表示将mat转化为array

K-Means的主要优点有：

　　　　1）原理比较简单，实现也是很容易，收敛速度快。

　　　　2）聚类效果较优。

　　　　3）算法的可解释度比较强。

　　　　4）主要需要调参的参数仅仅是簇数k。

K-Means的主要缺点有：

　　　　1）K值的选取不好把握

　　　　2）对于不是凸的数据集比较难收敛

　　　　3）如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。

　　　　4） 采用迭代方法，得到的结果只是局部最优。

　　　　5） 对噪音和异常点比较的敏感。

Kmeans算法的缺陷

       聚类中心的个数K 需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适
      Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。（可以使用Kmeans++算法来解决）

只适合凸数据集。

针对上述第2个缺陷，可以使用Kmeans++算法来解决

2.1、K-Means ++ 算法

Kmeans++算法，主要可以解决初始中心的选择问题，不可解决k的个数。

k-means++算法选择初始seeds的基本思想就是：初始的聚类中心之间的相互距离要尽可能的远。

  1. 从输入的数据点集合中随机选择一个点作为第一个聚类中心
  2. 对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
  3. 选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
  4. 重复2和3直到k个聚类中心被选出来
  5. 利用这k个初始的聚类中心来运行标准的k-means算法

 从上面的算法描述上可以看到，算法的关键是第3步，如何将D(x)反映到点被选择的概率上，一种算法如下：

  • 先从我们的数据库随机挑个随机点当“种子点”
  • 对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
  • 然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。
  • 重复2和3直到k个聚类中心被选出来
  • 利用这k个初始的聚类中心来运行标准的k-means算法

可以看到算法的第三步选取新中心的方法，这样就能保证距离D(x)较大的点，会被选出来作为聚类中心了。如下图 所示：  

                          

      假设A、B、C、D四个点与一个质心的距离为D(x)如上图所示，当算法取值Sum(D(x))*random时，该值会以较大的概率落入D(x)较大的区间内，所以对应的点会以较大的概率被选中作为新的聚类中心。

k-means++代码：http://rosettacode.org/wiki/K-means%2B%2B_clustering

from：Kmeans（K均值）与Kmeans++和KNN（K近邻）算法比较 

2.2、K-Means距离计算优化elkan K-Means

    在传统的K-Means算法中，我们在每轮迭代时，要计算所有的样本点到所有的质心的距离，这样会比较的耗时。那么，对于距离的计算有没有能够简化的地方呢？elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离的计算。那么哪些距离不需要计算呢？

　elkan K-Means利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质，来减少距离的计算。

　1、第一种规律是对于一个样本点x和两个质心\mu _{j_{1}},\mu _{j_{2}}。如果我们预先计算出了这两个质心之间的距离D(j_{1},j_{2})，则如果计算发现2D(x,j_{1})\leq D(j_{1},j_{2}),我们立即就可以知道D(x,j_{1})\leq D(x,j_{2})。此时我们不需要再计算D(x,j2),省了一步距离计算。

　2、第二种规律是对于一个样本点x和两个质心\mu _{j_{1}},\mu _{j_{2}}。我们可以得到D(x,j_{2})\geq max\begin{Bmatrix} 0,D(x,j_{1})-D(j_{1},j_{2})}{ \end{Bmatrix}这个从三角形的性质也很容易得到。

   利用上边的两个规律，elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本的特征是稀疏的，有缺失值的话，这个方法就不使用了，此时某些距离无法计算，则不能使用该算法。

2.3、Mini Batch K-Means算法

       Mini Batch K-Means算法是K-Means算法的变种，采用小批量的数据子集减小计算时间，同时仍试图优化目标函数，这里所谓的小批量是指每次训练算法时所随机抽取的数据子集，采用这些随机产生的子集进行训练算法，大大减小了计算时间，与其他算法相比，减少了k-均值的收敛时间，小批量k-均值产生的结果，一般只略差于标准算法。

该算法的迭代步骤有两步：

1：从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心

2：更新质心

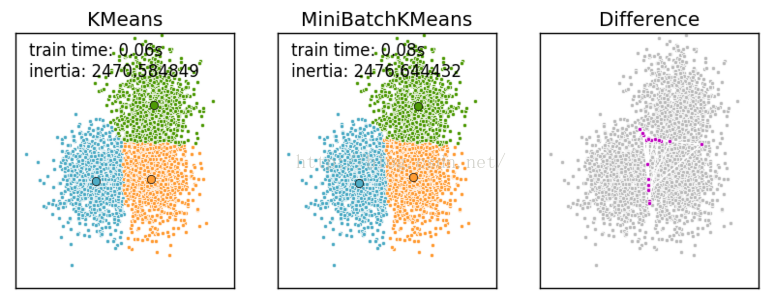
      与K均值算法相比，数据的更新是在每一个小的样本集上。对于每一个小批量，通过计算平均值得到更新质心，并把小批量里的数据分配给该质心，随着迭代次数的增加，这些质心的变化是逐渐减小的，直到质心稳定或者达到指定的迭代次数，停止计算Mini Batch K-Means比K-Means有更快的收敛速度，但同时也降低了聚类的效果，但是在实际项目中却表现得不明显,k-means和mini batch k-means的实际效果对比图:

          

如何选取合适的K值？

     K-means聚类方法，一般有人工设置K值，但是我们希望能从数据自身出发去确定真实的聚类数，也就是对数据而言的最佳聚类数。为此总结出主流的确定聚类数k的方法有以下两类。

1.手肘法

       手肘法的核心指标是SSE(sum of the squared errors，误差平方和)

                                                             

其中，C_{i}是第i个簇，p是C_{i}中的样本点，m_{i}是C_{i}的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。

       手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。这也是该方法被称为手肘法的原因。
     我们就是要求出随着k值的变化SSE的变化规律，找到SSE减幅最小的k值，这时k应该是相对比较合理的值。

  1. import pandas as pd
  2. from sklearn.cluster import KMeans
  3. import matplotlib.pyplot as plt
  4.  
  5. df_features = pd.read_csv(r'C:\预处理后数据.csv',encoding='gbk') # 读入数据
  6. '利用SSE选择k'
  7. SSE = []  # 存放每次结果的误差平方和
  8. for k in range(1,9):
  9.     estimator = KMeans(n_clusters=k)  # 构造聚类器
  10.     estimator.fit(df_features[['R','F','M']])
  11.     SSE.append(estimator.inertia_)
  12. X = range(1,9)
  13. plt.xlabel('k')
  14. plt.ylabel('SSE')
  15. plt.plot(X,SSE,'o-')
  16. plt.show()

k与SSE的关系图如下： 

                                

显然，肘部对于的k值为4，故对于这个数据集的聚类而言，最佳聚类数应该选4。

2、轮廓系数法

该方法的核心指标是轮廓系数（Silhouette Coefficient），某个样本点X_{i}的轮廓系数定义如下：

                                                            

其中，a是X_{i}与同簇的其他样本的平均距离，称为凝聚度，b是X_{i}与最近簇中所有样本的平均距离，称为分离度。而最近簇的定义是

                                                           

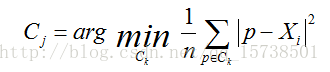
其中p是某个簇C_{k}中的样本。简单点讲，就是用X_{i}到某个簇所有样本的平均距离作为衡量该点到该簇的距离，选择离X_{i}最近的一个簇作为最近簇。

       找到最近簇后，求出(与X_{i}同一簇的)所有样本的轮廓系数，再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1]，且簇内样本的距离越近，簇间样本距离越远，平均轮廓系数越大，聚类效果越好。平均轮廓系数最大的k便是最佳聚类数。

      对于每个k值进行聚类并且求出相应的轮廓系数，然后做出k和轮廓系数的关系图:

  1. import pandas as pd
  2. from sklearn.cluster import KMeans
  3. from sklearn.metrics import silhouette_score
  4. import matplotlib.pyplot as plt
  5.  
  6. df_features = pd.read_csv(r'C:\Users\61087\Desktop\项目\爬虫数据\预处理后数据.csv',encoding='gbk')
  7. Scores = []  # 存放轮廓系数
  8. for k in range(2,9):
  9.     estimator = KMeans(n_clusters=k)  # 构造聚类器
  10.     estimator.fit(df_features[['R','F','M']])
  11.     Scores.append(silhouette_score(df_features[['R','F','M']],estimator.labels_,metric='euclidean'))
  12. X = range(2,9)
  13. plt.xlabel('k')
  14. plt.ylabel('轮廓系数')
  15. plt.plot(X,Scores,'o-')
  16. plt.show()

 得到聚类数k与轮廓系数的关系图：
                                   

       可以看到，轮廓系数最大的k值是2，这表示我们的最佳聚类数为2。但是，值得注意的是，从k和SSE的手肘图可以看出，当k取2时，SSE还非常大，所以这是一个不太合理的聚类数，我们退而求其次，考虑轮廓系数第二大的k值4，这时候SSE已经处于一个较低的水平，因此最佳聚类系数应该取4而不是2。

       但是，讲道理，k=2时轮廓系数最大，聚类效果应该非常好，那为什么SSE会这么大呢？在我看来，原因在于轮廓系数考虑了分离度b，也就是样本与最近簇中所有样本的平均距离。为什么这么说，因为从定义上看，轮廓系数大，不一定是凝聚度a（样本与同簇的其他样本的平均距离）小，而可能是b和a都很大的情况下b相对a大得多，这么一来，a是有可能取得比较大的。a一大，样本与同簇的其他样本的平均距离就大，簇的紧凑程度就弱，那么簇内样本离质心的距离也大，从而导致SSE较大。所以，虽然轮廓系数引入了分离度b而限制了聚类划分的程度，但是同样会引来最优结果的SSE比较大的问题，这一点也是值得注意的。
      从以上两个例子可以看出，轮廓系数法确定出的最优k值不一定是最优的，有时候还需要根据SSE去辅助选取，这样一来相对手肘法就显得有点累赘。因此，如果没有特殊情况的话，还是建议首先考虑用手肘法。
from :https://blog.csdn.net/qq_15738501/article/details/79036255

3、模糊c-均值聚类

     K-means算法是硬聚类算法，是典型的基于原型的目标函数聚类方法的代表，它是数据点到原型的某种距离作为优化的目标函数，利用函数求极值的方法得到迭代运算的调整规则。K-means算法以欧式距离作为相似度测度，它是求对应某一初始聚类中心向量V最优分类，使得评价指标J最小。算法采用误差平方和准则函数作为聚类准则函数。

                                                                     

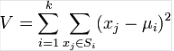
        模糊c-均值聚类算法 fuzzy c-means algorithm或称（ FCM）。在众多模糊聚类算法中， FCM算法应用最广泛且较成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而决定样本点的类属以达到自动对样本数据进行分类的目的。

        什么是隶属度？对于冷热程度，我们采取三个模糊子集：冷、暖、热。对于某一个温度，可能同时属于两个子集。要进一步具体判断，我们就需要提供一个描述“程度”的函数，即隶属度。

                                           

       相较于k-means的硬聚类，FCM提供了更加灵活的聚类结果。因为大部分情况下，数据集中的对象不能划分成为明显分离的簇，指派一个对象到一个特定的簇有些生硬，可能会出错。因此对每个对象和每个簇赋予一个权值，指明对象属于该簇的程度。基于概率的方法可以给出这样的权值，但有时候很难确定一个合适的统计模型，因此使用具有非概率特性的模糊c均值就是一个比较好的选择。

简单地说，就是要最小化损失函数J_f:

                                    

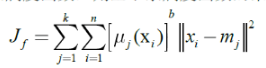
      其中，有n个样本点，k是聚类的簇数；j是类标号；表示样本x_i属于j类的隶属度。i表示第i个样本，x_i是具有d维特征的一个样本。m_j是j簇的中心，也具有d维度。

                            

通过迭代计算求解上式的最优解。

MATLAB函数： 
1. [center,U,obj_fcn] = FCM(Data,N_cluster,options); 
2. [center,U,obj_fcn] = FCM(Data,N_cluster);

输入变量 ：
data ---- n*m矩阵,表示n个样本,每个样本具有m维特征值 
cluster_n ---- 标量,表示聚合中心数目,即类别数 
options ---- 4*1列向量，其中 
options(1): 隶属度矩阵U的指数，>1(缺省值: 2.0) ，即公式里的指数b.
options(2): 最大迭代次数(缺省值: 100) 
options(3): 隶属度最小变化量,迭代终止条件(缺省值: 1e-5) 
options(4): 每次迭代是否输出信息标志(缺省值: 0) 

输出变量 
center ---- 聚类中心 
U ---- 隶属度矩阵 
obj_fcn ---- 目标函数值 

FCM用下列步骤确定聚类中心c_i和隶属矩阵U[1]：

1：用在0，1间的随机数初始化隶属矩阵U，

2：按式5，计算m个聚类中心m_i，i=1,…,m。

3：用式6 计算新的U矩阵。返回步骤2。

4：计算损失函数。如果它小于某个确定的阀值，或它相对上次价值函数值的改变量小于某个阀值，则算法停止。

matlab代码参考：https://blog.csdn.net/wzl1997/article/details/79264560

4、DBSCAN

     DBSCAN是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间的紧密相连的，在该类别任意样本周围不远处一定有同类别的样本存在。通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。

DBSCAN 算法是一种基于密度的聚类算法：
　　1.聚类的时候不需要预先指定簇的个数
　　2.最终的簇的个数不确定
DBSCAN算法将数据点分为三类：
　　1.核心点：在半径Eps内含有超过MinPts数目的点。
　　2.边界点：在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内的点。
　　3.噪音点：既不是核心点也不是边界点的点。

     如下图所示：图中黄色的点为边界点，因为在半径Eps内，它领域内的点不超过MinPts个，我们这里设置的MinPts为5；而中间白色的点之所以为核心点，是因为它邻域内的点是超过MinPts（5）个点的，它邻域内的点就是那些黄色的点！

                          

DBSCAN算法的流程

1.根据邻域条件遍历所有点，将所有点分别标记为核心点、边界点或噪声点；
2.删除噪声点；
3.为距离在Eps之内的所有核心点之间赋予一条边；
4.每组连通的核心点形成一个簇；
5.将每个边界点指派到一个与之关联的核心点的簇中（哪一个核心点的半径范围之内）。

DBSCAN小结

     和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数k，当然它最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点，这点和BIRCH算法类似。

　 那么我们什么时候需要用DBSCAN来聚类呢？一般来说，如果数据集是稠密的，并且数据集不是凸的，那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的，则不推荐用DBSCAN来聚类。

下面对DBSCAN算法的优缺点做一个总结。DBSCAN的主要优点有：

　　　　1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　　　2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　　　3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

　　　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　　　2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

　　　　3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

from：https://www.cnblogs.com/bonelee/p/8692336.html

from：https://www.cnblogs.com/pinard/p/6208966.html

5、Spectral Clustering谱聚类

      谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

     对于一个图G，我们一般用点的集合V和边的集合E来描述。即为G(V,E)。其中V即为我们数据集里面所有的点(v1,v2,...vn)。对于V中的任意两个点，可以有边连接，也可以没有边连接。我们定义权重w_{i,j}为点v_{i}和点v_{j}之间的权重。

         

    如何切图可以让子图内的点权重和高，子图间的点权重和低呢？对于上面这个图，假设点7和点8之间的权重值很小，那么很容易有红线所示的划分（假设二分），上面的代价函数计算出来的值很小。但显然绿色线所示才是最佳的分法。

传送门：https://www.cnblogs.com/pinard/p/6221564.html

              https://blog.csdn.net/songbinxu/article/details/80838865

5、层次聚类

      层次法（Hierarchicalmethods）先计算样本之间的距离。每次将距离最近的点合并到同一个类。然后，再计算类与类之间的距离，将距离最近的类合并为一个大类。不停的合并，直到合成了一个类。其中类与类的距离的计算方法有：最短距离法，最长距离法，中间距离法，类平均法等。比如最短距离法，将类与类的距离定义为类与类之间样本的最短距离。

      凝聚型层次聚类的策略是先将每个对象作为一个簇，然后合并这些子簇为越来越大的簇，直到所有对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类，它们只是在簇间相似度的定义上有所不同。 这里给出采用最小距离的凝聚层次聚类算法流程：

(1) 将每个对象看作一类，计算两两之间的最小距离；

(2) 将距离最小的两个类合并成一个新类；

(3) 重新计算新类与所有类之间的距离；

(4) 重复(2)、(3)，直到所有类最后合并成一类。

     另外我们可以看出凝聚的层次聚类并没有类似基本K均值的全局目标函数，没有局部极小问题或是很难选择初始点的问题。合并的操作往往是最终的，一旦合并两个簇之后就不会撤销。当然其计算存储的代价是昂贵的。

层次聚类的优缺点

优点：1，距离和规则的相似度容易定义，限制少；2，不需要预先制定聚类数；3，可以发现类的层次关系；4，可以聚类成其它形状

缺点：1，计算复杂度太高；2，奇异值也能产生很大影响；3，算法很可能聚类成链状

from：https://blog.csdn.net/andy_shenzl/article/details/83783469

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家小花儿/article/detail/517672
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号