机器学习----混淆矩阵(Confusion Matrix)

混淆矩阵(Confusion Matrix)

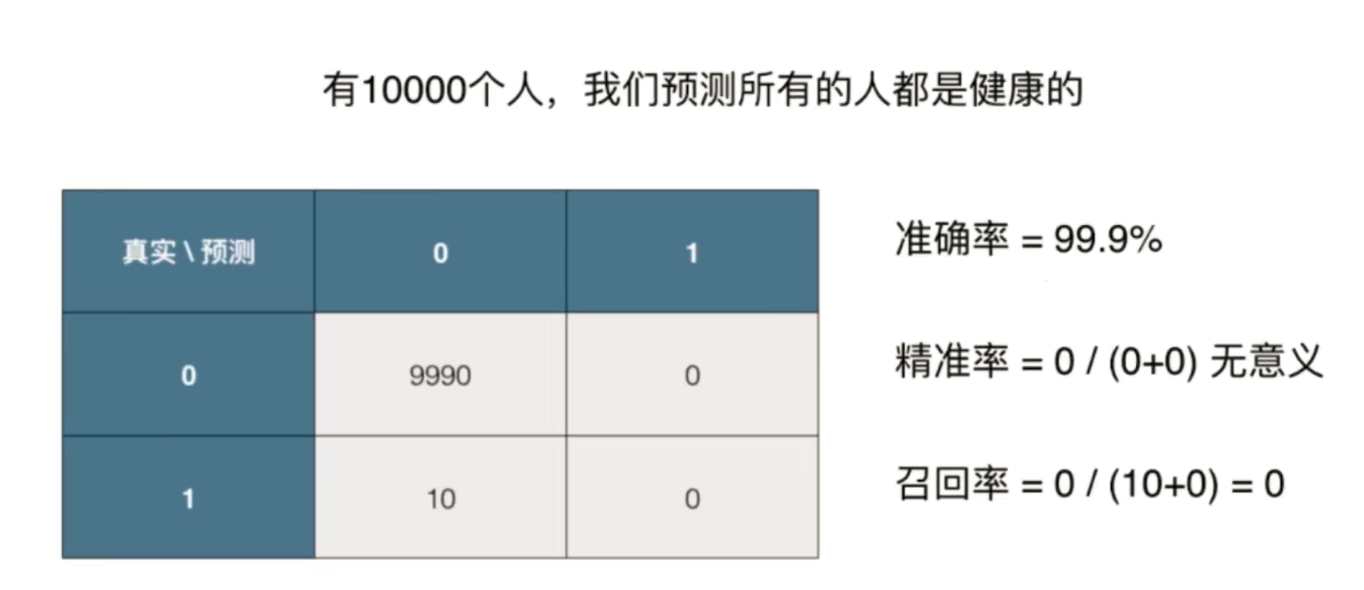
假设有一个算法，其预测某种癌症的准确率为99.9%。这个算法好吗？
99.9%的准确率看上去很高，但是如果这种癌症本身的发病率只有0.1%，即使不训练模型而直接预测所有人都是健康人，这样的预测的准确率也能达到99.9%。 更极端的情况，如果这种癌症本身的发病率只有0.01%，这算法预测的准确率还不如直接预测所有人都健康。 对于极度偏斜的数据(癌症患者的人数和健康人数量差别特别大)（skewed data），用准确率评价分类算法好坏有局限性.]

解决方法：混淆矩阵

工具：混淆矩阵，以二分类为例

0 - Negative - 阴性, 1 - Positive - 阳性
1是我们关注的部分。

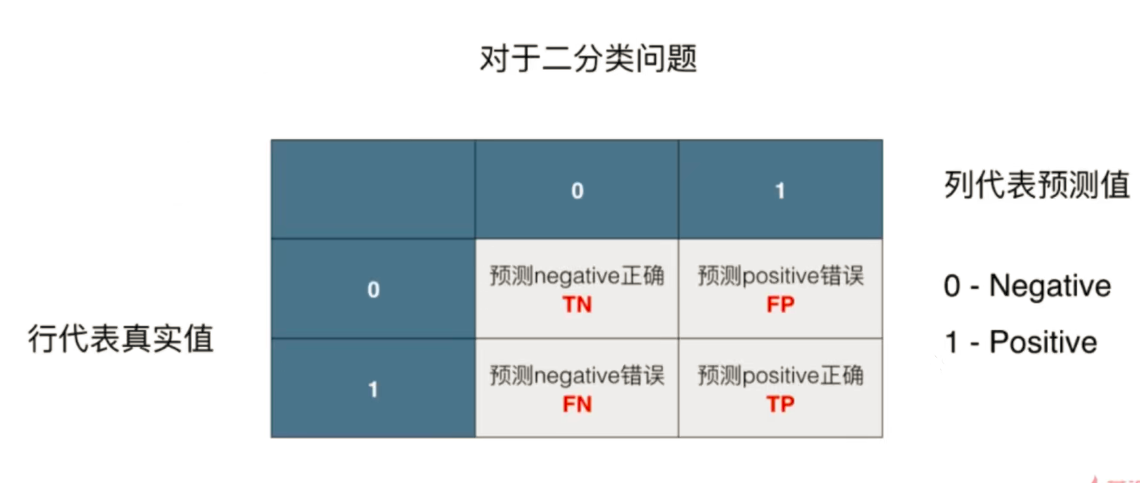
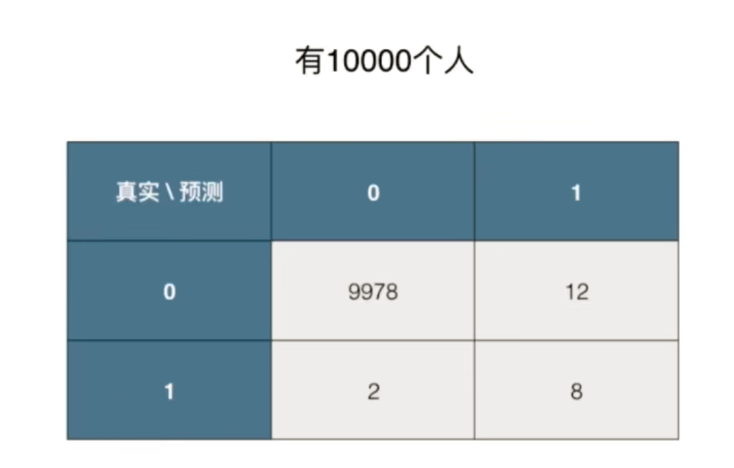
00位置代表有9978人真实没患癌症; 模型预测9978人也没患癌症
01位置代表有12人没患癌症; 模型却预测12人患了癌症
11位置代表有2人患了癌症; 模型却预测2人没患癌症
12位置代表有8人患了癌症; 模型预测8人患了癌症

精确率和召回率

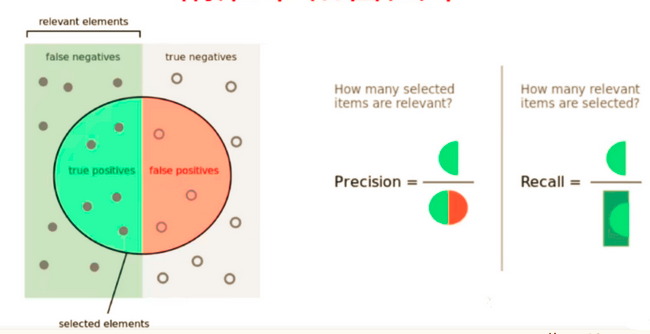
精准率 precision = TP / (TP + FP)

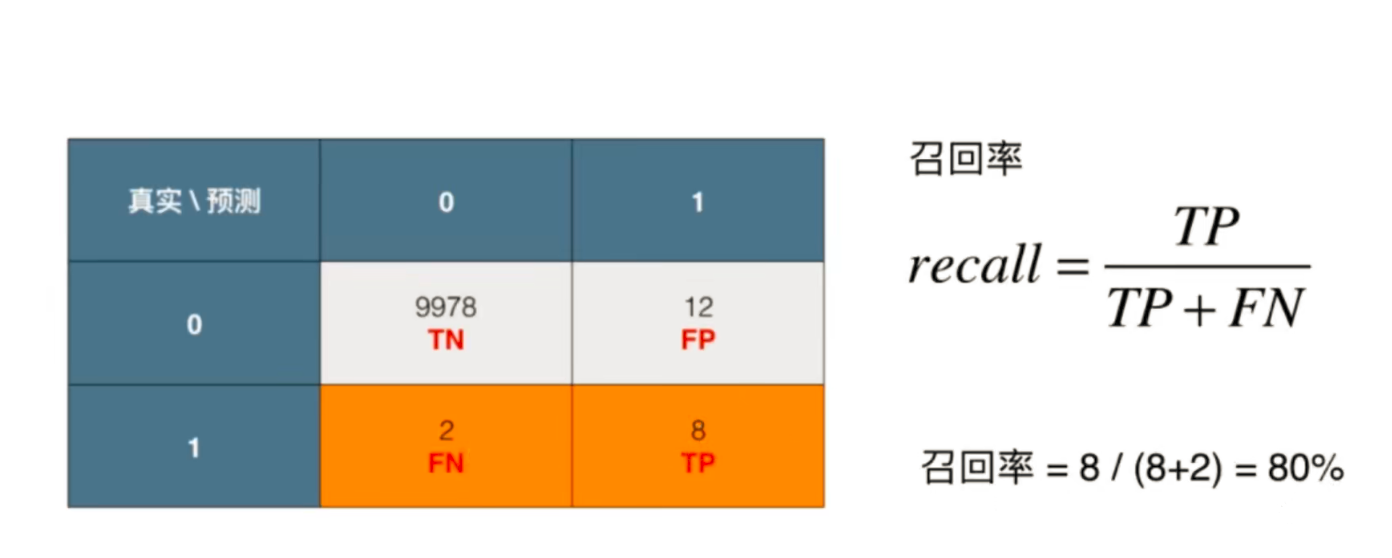
召回率 recall = TP / (TP + FN)

在有偏数据中，将1作为真正关注的事件

精准率：预测的关注事件（1）中预测对了的概率

### 召回率: 表示 我们算法在已经发生的事件中正确预测个数的比率。

使用混淆矩阵的好处

回到之前列举的癌症预测案例, 如果某种癌症的发病率为0.1%，那么预测所有人都健康的模型，虽然准确率达到99.9%。但精准率没有意义，召回率为0，可见这个模型是个无效的模型, 所以混淆矩阵可以作为季度偏斜的数据的评价指标

实现混淆矩阵、精准率、召回率

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0    # 产生极度偏斜的数据

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

准确度

log_reg.score(X_test, y_test)
1

输出：0.9755555555555555

混淆矩阵

y_log_predict = log_reg.predict(X_test)

def TN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict==0))   # 注意这里是一个‘&’

TN(y_test, y_log_predict)   # 403

def FP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict==1))

FP(y_test, y_log_predict)   # 2

def FN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict==0))

FN(y_test, y_log_predict)   # 9

def TP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict==1))

TP(y_test, y_log_predict)   # 36

def confusion_matrix(y_true, y_predict):
    return np.array([
        [TN(y_true, y_predict), FP(y_true, y_predict)],
        [FN(y_true, y_predict), TP(y_true, y_predict)]
    ])

confusion_matrix(y_test, y_log_predict)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

输出结果：
array([[403, 2], [ 9, 36]])

精准率

def precision_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fp = FP(y_true, y_predict)
    try:
        return tp / (tp + fp)
    except:   # 处理分母为0的情况
        return 0.0

precision_score(y_test, y_log_predict)
1
2
3
4
5
6
7
8
9

def recall_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)

    try:
        return tp / (tp + fn)
    except:
        return 0.0

recall_score(y_test, y_log_predict)
1
2
3
4
5
6
7
8
9
10

输出结果：0.8

scikit-learn中的混淆矩阵、精准率、召回率

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_log_predict)

from sklearn.metrics import precision_score
precision_score(y_test, y_log_predict)

from sklearn.metrics import recall_score
recall_score(y_test, y_log_predict)
1
2
3
4
5
6
7
8

0.8

F1 score

对于极度偏斜的数据，使用指标精准率和召回率都优于使用指标分类准确度。
但精准率和召回率是两个指标。如果一个算法的精准率和召回率表现不同，该如何取舍这两个指标？
解决方法1：视具体场景而定。
有时我们注重精准率，比如股票预测，我们希望预测股票为升结果都是准确的（否则可能亏钱），而不在意错过另一些错过的股票上升的机会（错过一些赚钱的机会）。
有时我们注重召回率，比如病人诊断。我们希望得病的人都能识别出来（否则这些人可能会病情恶化），而有一些没得病的人被错误地识别出来没有关系（这些人做进一步检查即可）。
解决方法2：同时关注精准率和召回率，即新指标：F1 score

指标：F1 score

F1 score是precision和recall的调和平均值。

调和平均值的特点：如果precision和recall非常不平衡，则F1 score也是比较低的。只有两者都高，F1 score才会高。
F1 score的取值范围：[0, 1]

def f1_score(precison, recall):
    try:
        return 2*precison*recall /(precison + recall)
    except:
        return 0.0
1
2
3
4
5

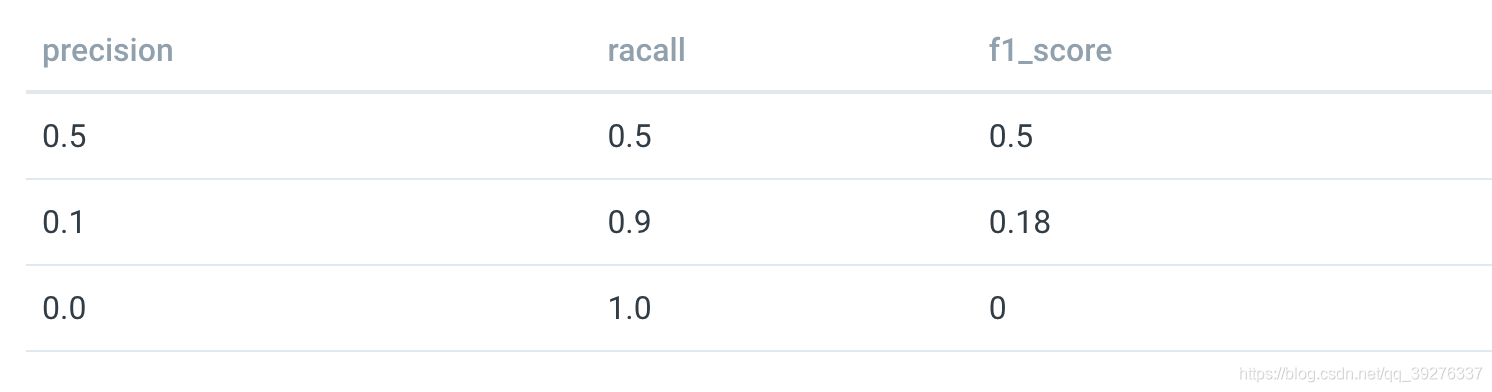
precision和recall取不同的值对f1_score的影响

F1 score来评价手写数字的识别效果

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
y[digits.target==9] = 1
y[digits.target!=9]= 0  # 产生极度偏斜的数据
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
from sklearn.linear_model import LogisticRegression
log_reg  = LogisticRegression()
log_reg.fit(X_train, y_train)
y_log_predict = log_reg.predict(X_test)
from sklearn.metrics import accuracy_score, mean_squared_error, confusion_matrix
from sklearn.metrics import precision_score, recall_score
precison = precision_score(y_test, y_log_predict)
recall = recall_score(y_test, y_log_predict)
f1_score(precison, recall)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

输出：0.8674698795180723
对有偏数据，指标F1 score优于分类准确度。

Precision-Recall平衡

我们总是希望精准率和召回率这两个指标都尽可能地高。但事实上精准率和召回率是互相矛盾的，我们只能在其中找到一个平衡。
以逻辑回归为例来说明精准率和召回率之间的矛盾关系，以下是逻辑回归的公式：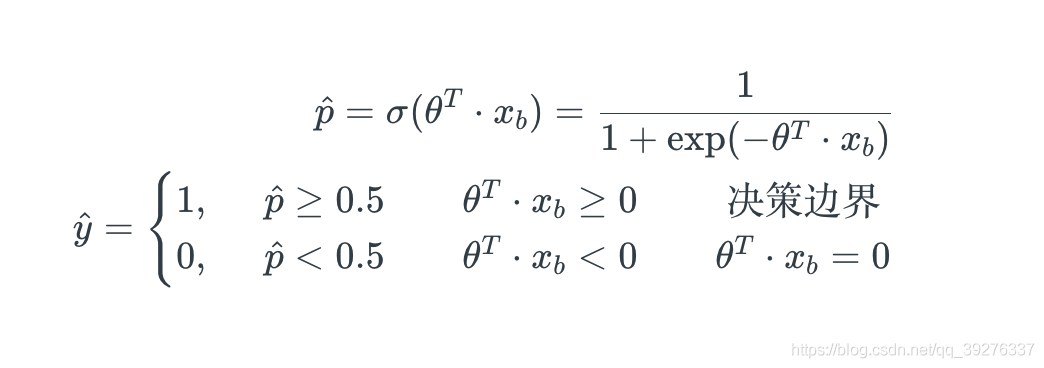
在这里决策边界是以0为分界点，如果把0改成一个自定义的threshold，threshold的改变会平移决策边界，从而影响精准率和召回率的结果。

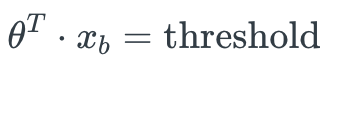
threshold是怎样影响精准率和召回率的

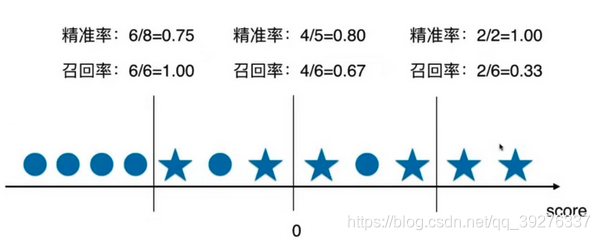
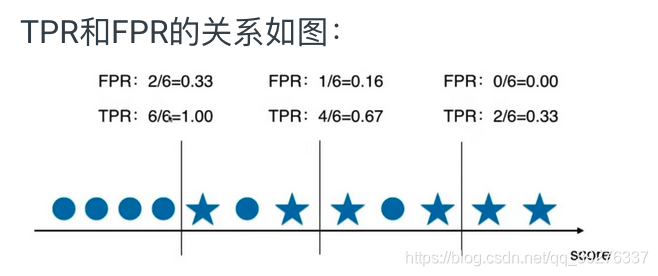
如图，图中的直线代表决策边界，决策边界右边的样本分类为1，决策边界左边的样本分类为0。图中五角星为实际类别为1的样本，0为实际类别为0的样本。
如果以0为分界点，精准率 = 4/5 = 0.0，召回率 = 4 / 6 = 0.67
分界点往右移，则精准率提升，召回率降低。
分界点往左移，则精准率下降，召回率提升。

下面使用LR对手写数字分类的例子来说明分界点移动对精准率和召回率的影响

# 数据
import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# 训练模型
import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# 模型指标
log_reg.score(X_test, y_test)   #  0.9755555555555555

y_predict = log_reg.predict(X_test)

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_predict)   # array([[403,   2], [  9,  36]], dtype=int64)

from sklearn.metrics import precision_score
precision_score(y_test, y_predict)   # 0.9473684210526315

from sklearn.metrics import recall_score
recall_score(y_test, y_predict)   # 0.8

from sklearn.metrics import f1_score
f1_score(y_test, y_predict)   # 0.8674698795180723
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

移动LogisticRegression的分界点
分析LogisticRegression当前使用的分界点

上文中提到，通过调整threshold来移动决策边界，但sklearn并没有直接提供这样的接口。自带predict函数都是以0作为threshold的。
但sklearn提供了决策函数，把X_test传进去，得到的是每个样本的score值。predict函数就是根据样本的score值来判断它的分类结果。

log_reg.decision_function(X_test)
1

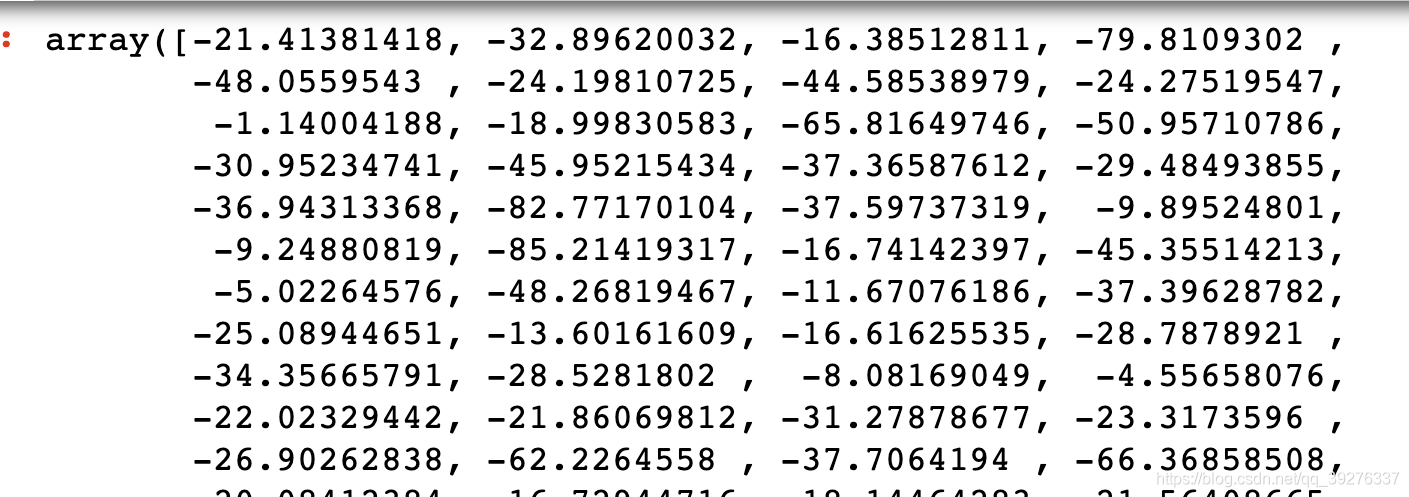
例如前60个样本的score值是这样的，那么它们的predict结果0的决策函数值小于0, 1的大于零

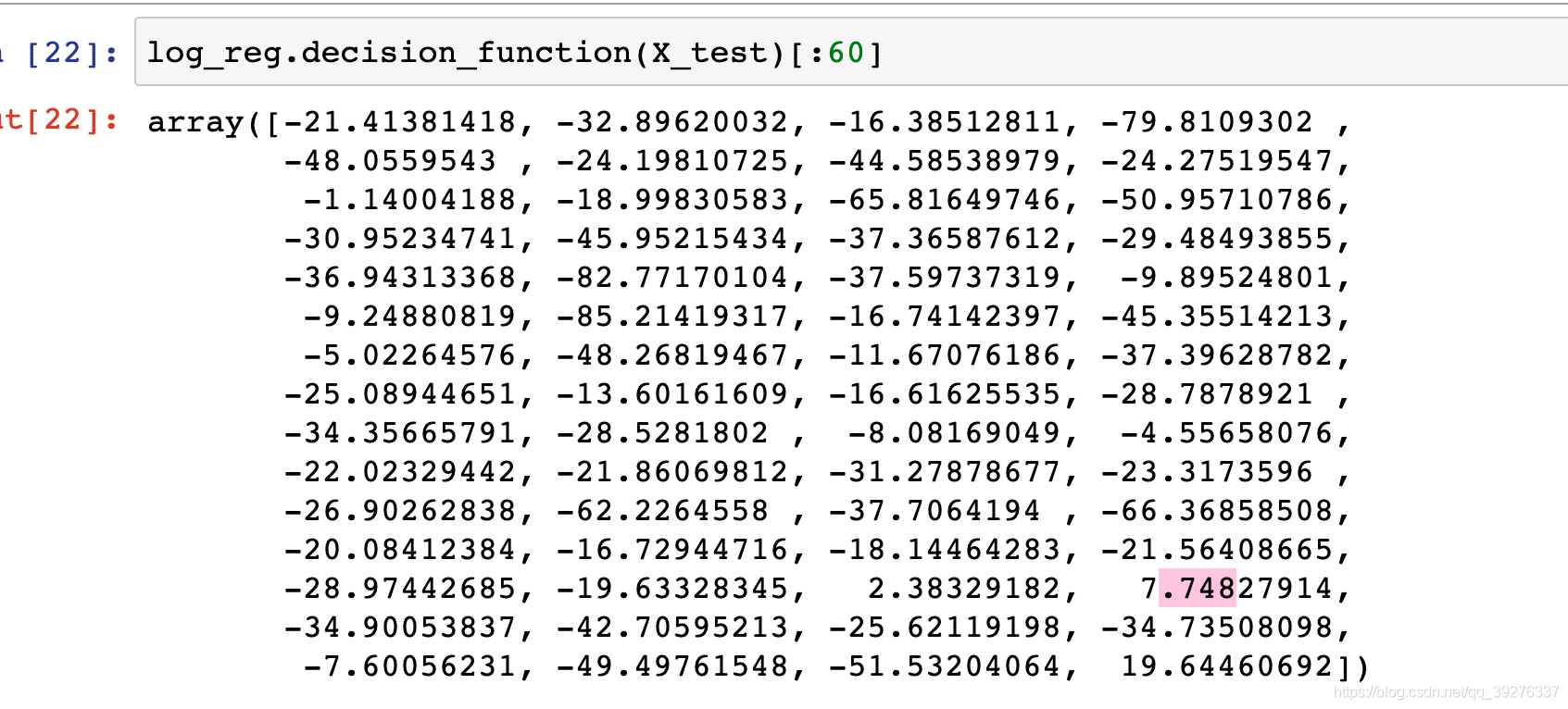
所以可以基于decision_function来移动决策边界。

decision_scores = log_reg.decision_function(X_test)
np.min(decision_scores)   # -85.68608522646575
np.max(decision_scores)   # 19.8895858799022
1
2
3

移动threshold: 0->5

y_predict_2 = np.array(decision_scores >= 5, dtype='int')
confusion_matrix(y_test, y_predict_2)   # array([[404,   1], [ 21,  24]], dtype=int64)
precision_score(y_test, y_predict_2)   # 0.96
recall_score(y_test, y_predict_2)   # 0.5333333333333333
1
2
3
4

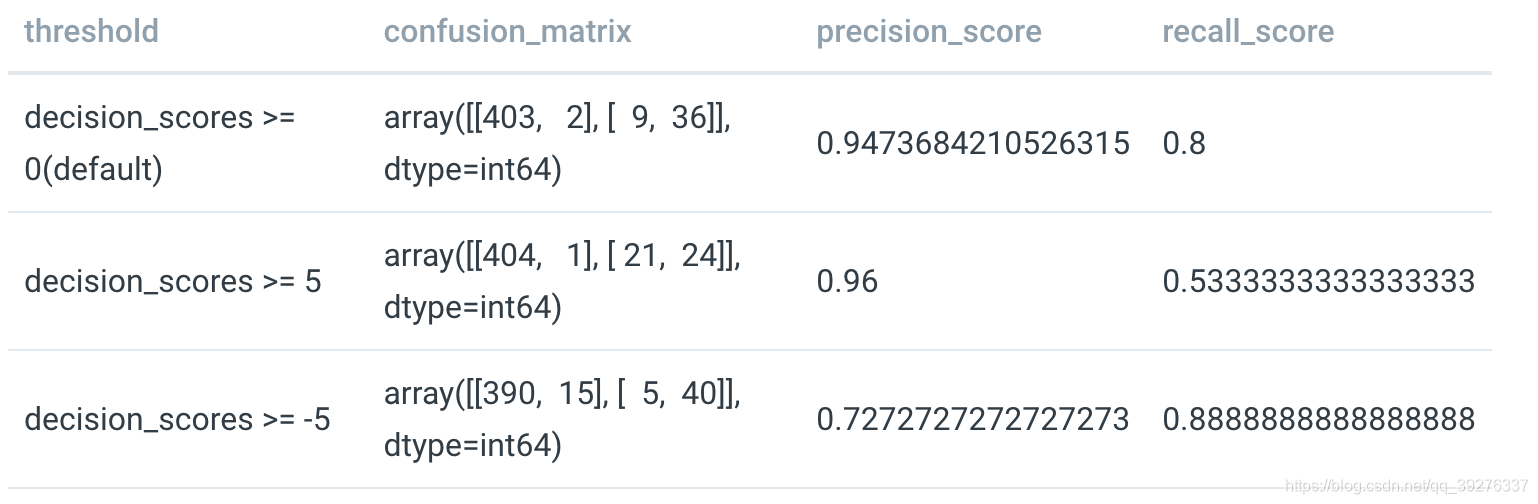
precision-recall曲线

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

输出：0.9755555555555555
skleran的LogisticRegression中，通过discision score和threshold来判断分类结果。
默认情况下threshold = 0。调整threshold值，精准率和召回率就会相应的变化。接下来通过可视化的方式表现threshold和精准率、召回率之间的关系。

精准率和召回率的变化曲线

precision_scores = []
recall_scores = []
thresholds = np.arange(np.min(decision_scores),np.max(decision_scores),step=0.1)
for threshold in thresholds:
    y_predict = np.array(decision_scores >= threshold, dtype='int')
    precision_scores.append(precision_score(y_test, y_predict))
    recall_scores.append(recall_score(y_test, y_predict))
plt.plot(thresholds, precision_scores, label='precision_score')
plt.plot(thresholds, recall_scores, label='recall_score')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11

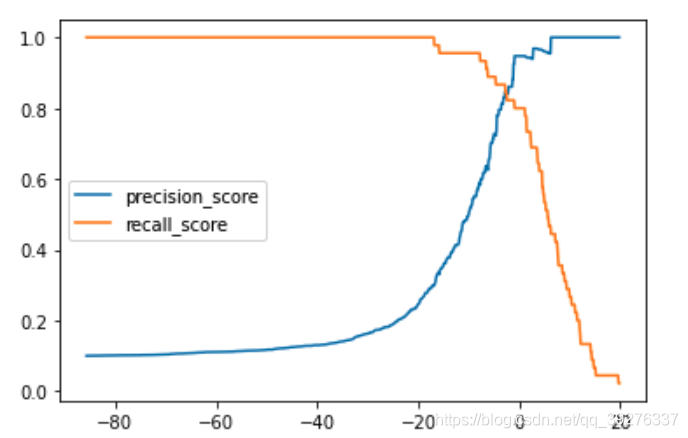
绘制precision-recall曲线

plt.plot(precision_scores, recall_scores)
plt.show()
1
2

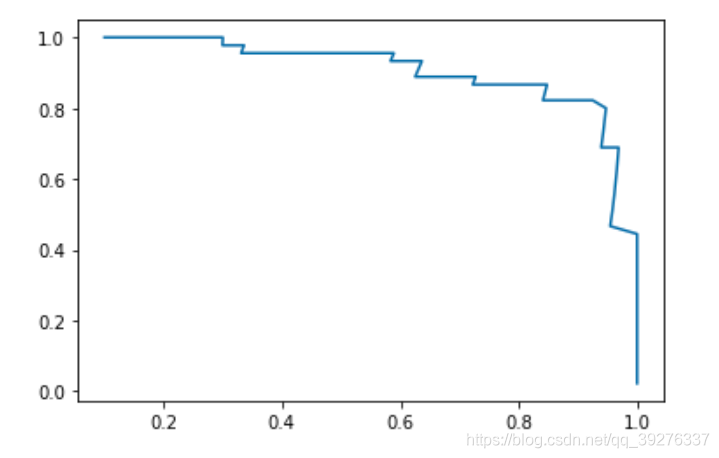
scikit-learn中的precision-recall曲线

from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_test, decision_scores)
plt.plot(thresholds, precisions[:-1], label='precision_score')
plt.plot(thresholds, recalls[:-1], label='recall_score')
plt.legend()
plt.show()
1
2
3
4
5
6

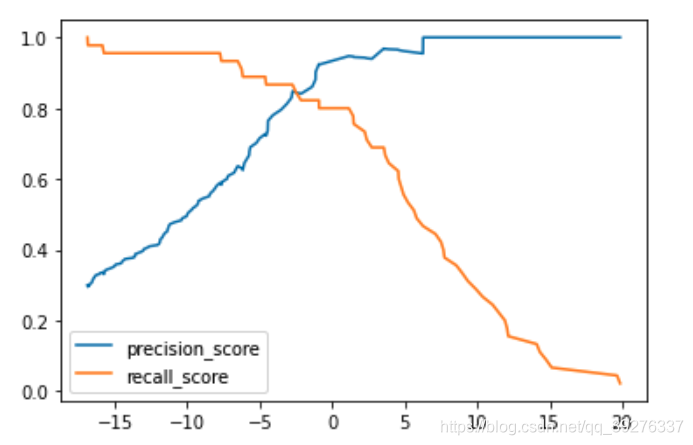
Note 1:precisions.shape = (151,)，recalls.shape = (151,)，thresholds.shape = (150,)，这是因为“the last precision and recall values are 1. and 0. respectively and do not have a corresponding threshold.”
Note 2：sklearn提供的precision-recall曲线自动只寻找了我们最关心的那一部分。

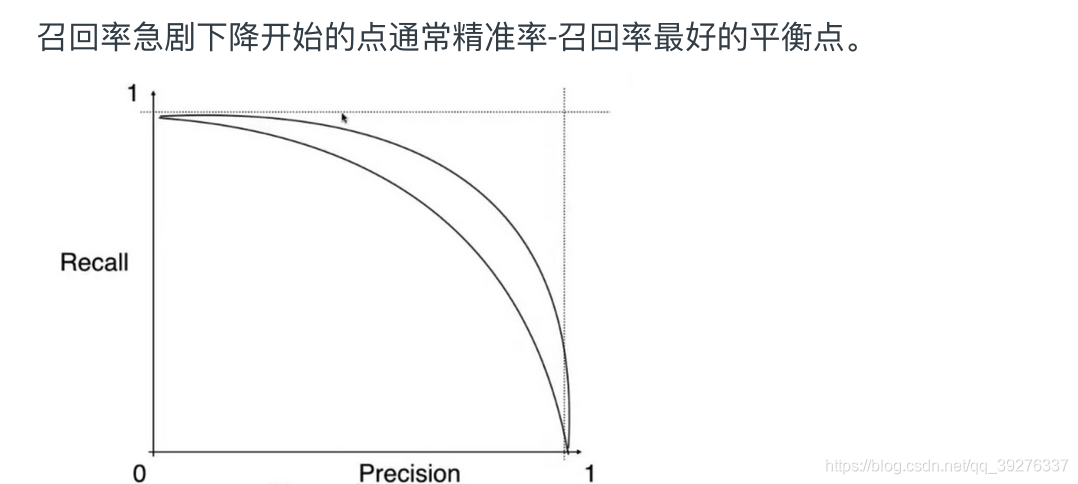
精准率-召回率曲线整体上是这样的曲线。用不同的算法或相同的算法的不同的超参数都能训练出各自的模型。每种模型都有不同的精准率-召回率曲线。
假如如图是两个模型的精准率-召回率曲线，那么明显可以得出结论外面曲线的模型优于里面曲线的模型。因此PR曲线也可以作为选择模型/超参数的指标。

ROC曲线

ROC：Receiver Operation Characteristic Curve
ROC曲线描述TPR和FPR之间的关系。

• TPR = recall = TP / (TP + FN) # true positive rate
• FPR = FP / (FP + TN) # false positive rate
  

def TN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict==0))   # 注意这里是一个‘&’

def FP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict==1))

def FN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict==0))

def TP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict==1))

def confusion_matrix(y_true, y_predict):
    return np.array([
        [TN(y_true, y_predict), FP(y_true, y_predict)],
        [FN(y_true, y_predict), TP(y_true, y_predict)]
    ])

def precision_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fp = FP(y_true, y_predict)
    try:
        return tp / (tp + fp)
    except:   # 处理分母为0的情况
        return 0.0

def recall_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)

    try:
        return tp / (tp + fn)
    except:
        return 0.0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

TPR和FPR

def TPR(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)

    try:
        return tp / (tp + fn)
    except:
        return 0.0

def FPR(y_true, y_predict):
    fp = FP(y_true, y_predict)
    tn = TN(y_true, y_predict)

    try:
        return fp / (fp + tn)
    except:
        return 0.0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

加载数据

def TPR(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)

    try:
        return tp / (tp + fn)
    except:
        return 0.0

def FPR(y_true, y_predict):
    fp = FP(y_true, y_predict)
    tn = TN(y_true, y_predict)

    try:
        return fp / (fp + tn)
    except:
        return 0.0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

绘制TFP和FRP的曲线，即ROC

decision_scores = log_reg.decision_function(X_test)
import matplotlib.pyplot as plt

fprs = []
tprs = []

thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), step=0.1)
for threshold in thresholds:
    y_predict = np.array(decision_scores >= threshold, dtype='int')
    fprs.append(FPR(y_test, y_predict))
    tprs.append(TPR(y_test, y_predict))

plt.plot(fprs, tprs)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14

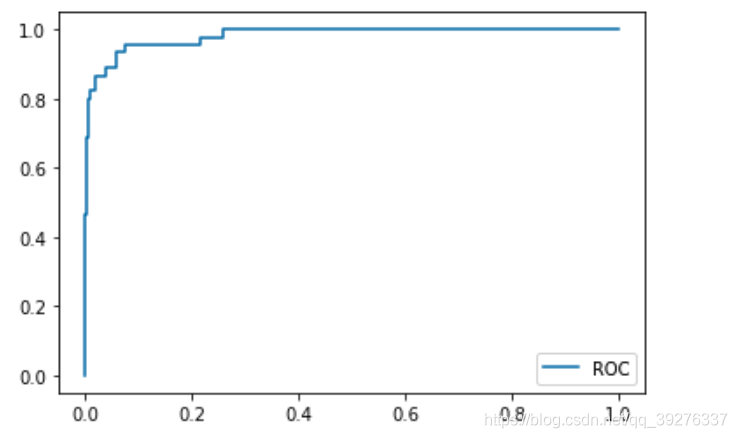
sklearn中的ROC曲线

from sklearn.metrics import roc_curve

fprs, tprs, thresholds = roc_curve(y_test, decision_scores)
plt.plot(fprs, tprs)
plt.show()

1
2
3
4
5
6

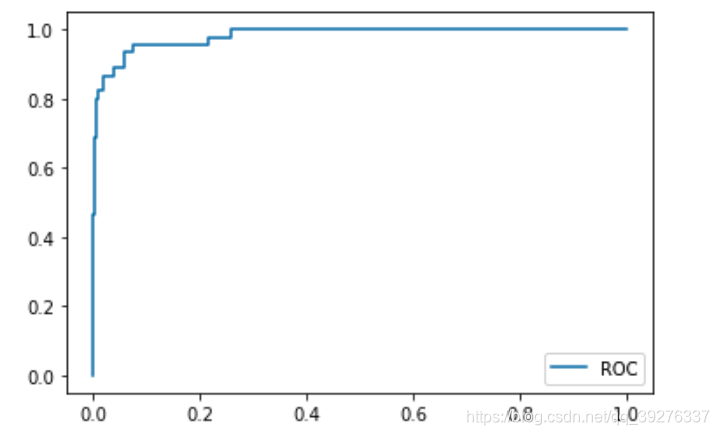
我们通常关注这条曲线下面的面积。面积越大，说明分类的效果越好。

ROC score

ROC score代码曲线下面的面积。
auc = area under cur

from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, decision_scores)
1
2

输出：0.9830452674897119

总结

对于有偏数据，观察它的精准率和召回率是非常有必要的。
但是ROC曲线对有偏数据并不敏感，它主要用于比较两个模型的孰优孰劣

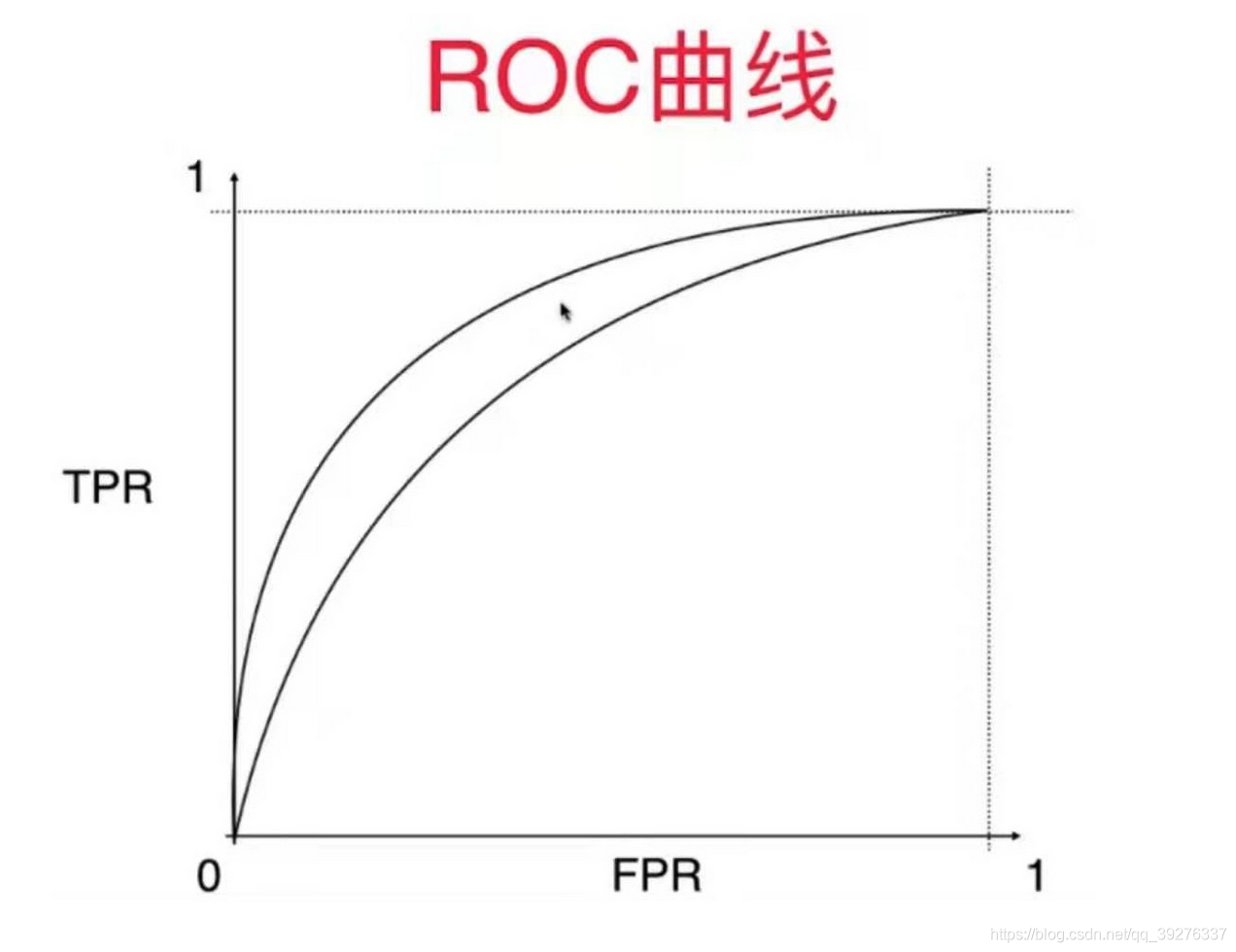
如果两根曲线分别代码两个模型的ROC曲线，在这种情况下我们会选择外面那根曲线对应模型。
ROC曲线的横轴就是FPRate，纵轴就是TPRate，当二者相等时，表示的意义则是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的，此时AUC为0.5

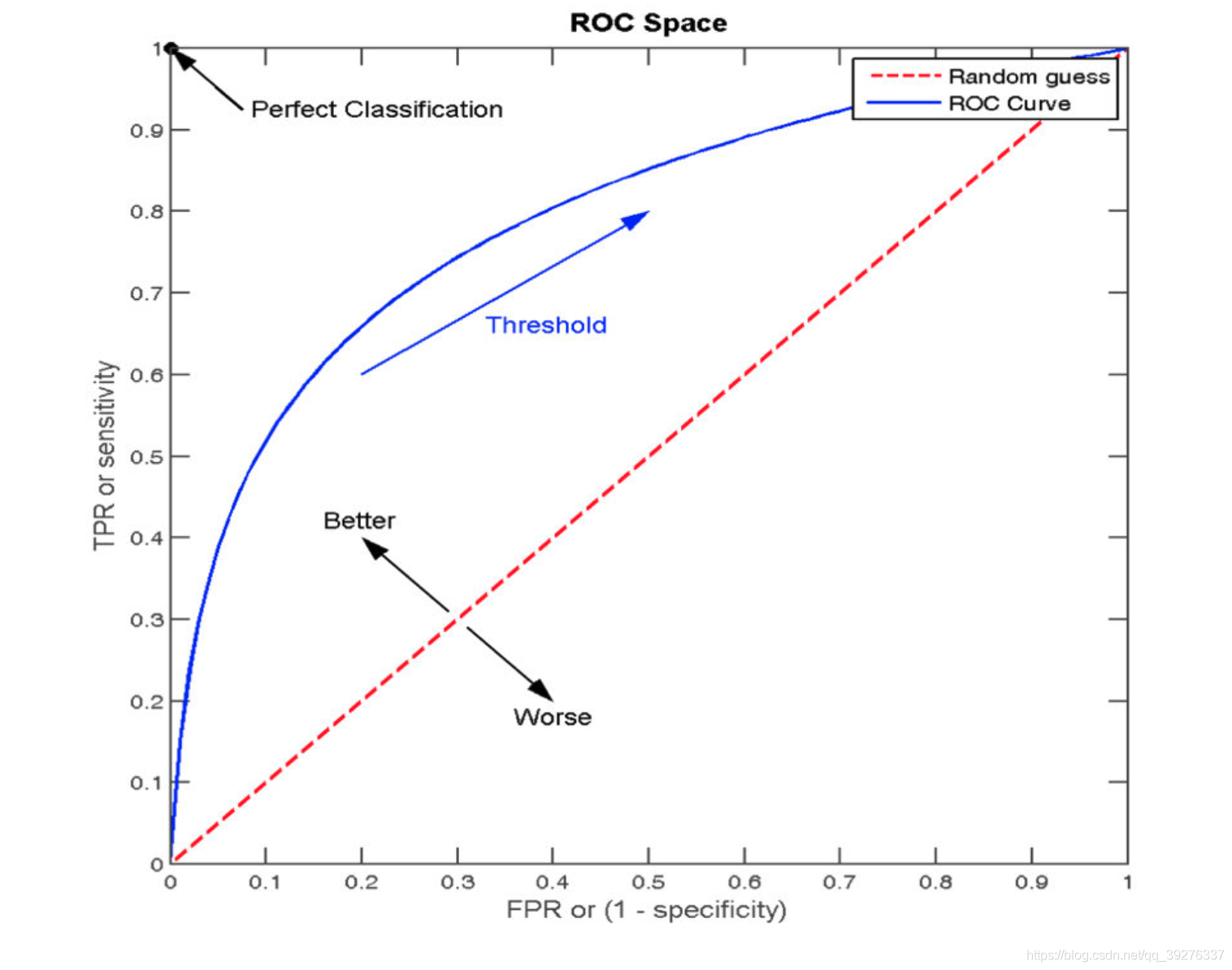
AUC指标

• AUC的概率意义是随机取一对正负样本，正样本得分大于负样本得分的概率
• AUC的范围在[0, 1]之间，并且越接近1越好，越接近0.5属于乱猜
• AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5<AUC<1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。