Numpy的用法详细总结_numpy使用

前言

• Numpy（Numerical Python），Python的一种开源的数值计算扩展

• 我觉得比较简单好理解的显示结果就不会在文中再体现出来，我更愿意在这篇博客中写下我遇到过的坑，以及自己对于一些方法的个人理解，如果读者有需要还是更建议全部自己敲一遍。我学的时候是全部都自己敲了一遍，并在这过程中才能发现许多问题。代码看着简单，其实并不简单，谁敲谁知道。

---

1. 创建不同类型的array

直接使用numpy中的array方法就可以创建数组了，如果输入的是一个列表则创建数组，输入多个列表这样数据就有两个维度就会变成矩阵了。除了我们直接手动指明数组内容的创建方式，numpy中还提供一些快速操作，如创建全0数组，全1数组等便捷操作，下面进行具体展开。

1.1 创建一维数组 array

import numpy as np
# 一维array
a = np.array([2,23,4], dtype=np.int32) # np.int默认为int32，dtype可以指定array的数据类型
print(a)
print(a.dtype)  #显示array的数据类型
1
2
3
4
5

1.2 创建二维数组（矩阵）array

# 多维array
a = np.array([[2,3,4],
              [3,4,5]])
print(a) # 生成2行3列的矩阵
1
2
3
4

1.3 创建全0数组 zeros

a = np.zeros((3,4))
print(a) # 生成3行4列的全零矩阵
1
2

1.4 创建全1数组 ones

# 创建全一数据，同时指定数据类型
a = np.ones((3,4),dtype=np.int)
print(a)
1
2
3

1.5 创建全空数组 empty

如何表示空的概念？其实这边创建出来数组中的数据都是无限小的、无限接近于0但不是0，这方便我们数学上的一些操作

# 创建全空数组，其实每个值都是接近于零的数
a = np.empty((3,4))
print(a)
1
2
3

[[6.23042070e-307 3.56043053e-307 1.37961641e-306 2.22518251e-306]
[1.33511969e-306 6.23037317e-307 6.23053954e-307 1.37962185e-306]
[1.11261027e-306 6.89805151e-307 1.78020169e-306 1.42410974e-306]]

1.6 创建有连续序列的数组 arange

和Python中的range()类似，同样是要指定起始点和终止点，可以指定步长或者反向步长，同样是左开右闭。但是range就不能直接返回一个列表了

# 创建连续数组
a = np.arange(10,21,2) # 10-20的数据，步长为2
print(a)
1
2
3

• 直接使用numpy中的arange方法得到的是一个一维数组，那如果我们想要创建出一个矩阵中数据是连续的该怎么办？我们还是先用arange把数据用一维数组的形式存储好，然后再使用reshape重塑数组维度，改造成矩阵形式。
• reshape的本质就是把原本数组中的元素按顺序展开来，然后依次填入新定义的尺寸中去。

# 使用reshape改变上述数据的形状
b = a.reshape((2,3))
print(b)
1
2
3

• 但是重塑时要注意，我们重塑数组指定的尺寸大小是否和原本arange数组的尺寸大小一样，大一点和小一点都会报错，改造不能乱改造，必须基于原先arange数组的特点进行改变排列。报错时则会出现如下错误
  

1.7 创建有连续间隔的数组 linspace

也可以称为线性等分向量（linear space），在一个指定区间内按照指定的步长，将区间均等分，生成的是一个线段类型的数组。生成的线性间隔数据中，是有把区间的两端加进去的

# 创建线段型数据
a = np.linspace(1,10,20) # 开始端1，结束端10，且分割成20个数据，生成线段
print(a)
1
2
3

• 同样，在这边我们也可以用reshape重新改造数组中数据的排列方式

# 同时也可以reshape
b = a.reshape((5,4))
print(b)
1
2
3

1.8 创建随机数组 random.rand

利用random.rand() 可以创建出指定尺寸的数组

a = np.random.rand(3,4)
b = np.random.rand(2)
print(a,"\n",b)
1
2
3

---

2. 关于数组信息的显示操作

这些方法都是用上面方法创建出来的数组的内置方法

2.1 数组的维度 ndim

print('number of dim:', array.ndim)
1

2.2 数组各个维度上的长度 shape

print('shape:',array.shape)
1

2.3 数组中的元素个数 size

print('size:',array.size)
1

2.4 数组的数据类型 dtype

对数组使用astype()可以转换数据类型。

print('type',array.dtype)
1

---

3. 一维数组的基本运算

先假设现在有两个一维数组

import numpy as np
# 一维矩阵运算
a = np.array([10,20,30,40])
b = np.arange(4)
print(a,b)
1
2
3
4
5

3.1 加减法

会在两个数组的相同对应位置上进行相加减，然后返回各个位置被相加减后结果的同样尺寸数组

c = a - b
d = a + b
print(c,d)
1
2
3

[10 19 28 37]
[10 21 32 43]

3.2 乘除法

将对应的元素相乘除，返回的是同样尺寸的数组

c = a * b
d = b / a
print(c)
print(d)
1
2
3
4

[ 0 20 60 120]
[0. 0.05 0.06666667 0.075 ]

3.3 点乘（内积和）

两种方法在一维数组中效果中都一样，都是返回对应元素相乘后相加的结果，返回的是一个数值

c = a.dot(b)
d = np.dot(a,b)
print(c)
print(d)
1
2
3
4

200
200

3.4 数组的指数

和Python中指数的写法一样，直接对array进行指数运算**就行了

# 在Numpy中，想要求出矩阵中各个元素的乘方需要依赖双星符号 **，以二次方举例，即：
c = b**2
print(c)
1
2
3

3.5 一维数组转换为矩阵

print(A[np.newaxis,:]) # [1 1 1]变为[[1 1 1]]
1

[[1 1 1]]

print(A[np.newaxis,:].shape) # (3,)变为(1, 3)
1

(1, 3)

print(A[:,np.newaxis])
1

[[1]
[1]
[1]]

3.6 数组与标量的运算

数组除了可以与数组进行运算之外，还可以与标量进行加减乘除，其结果就是数组中的每一个元素都与标量进行运算后汇总后的结果

data1 = np.array([[1, 2, 3], [4, 5, 6]])
data2 = 10
print(data1 + data2)     # 数组相加
1
2
3

[[11, 12, 13]
[14, 15, 16]]

pritn(data1 * data2)  #数组相乘
1

[[10, 20, 30],
[40, 50, 60]]

3.7 两个数组之间的比较

• 返回两个数组对应位置上的最值

x = np.array([12, 9, 13, 15]
y = np.array([11, 10, 4, 8]

np.maximum(x, y)  # 两个数组元素级最大值的
1
2
3
4

[12, 10, 13, 15]

-返回两个数组对应位置上比较谁更大后的结果

np.greater(x, y)  # 执行元素级的比较操作
1

[ True, False, True, True]

---

4. 多维数组的基本运算

首先创建两个二维数组

a = np.array([[1,1],[0,1]])
b = np.arange(4).reshape((2,2))

print(a)
print(b)
1
2
3
4
5

[[1 1]
[0 1]]

[[0 1]
[2 3]]

4.1 多维数组的矩阵乘法

多维数组有两种乘法，同样是用dot，但是这边dot用法和前面提到的一维数组中的点乘不一样，这边dot是用于矩阵乘法的。

# 多维度矩阵乘法
# 第一种乘法方式:
c = a.dot(b)
print(c)

# 第二种乘法:
c = np.dot(a,b)
print(c)
 
# 多维矩阵乘法不能直接使用'*'号
1
2
3
4
5
6
7
8
9
10

[[2 4]
[2 3]]

4.2 多维数组的转置

print(A)
1

[[14 13 12 11]
[10 9 8 7]
[ 6 5 4 3]]

# 矩阵转置
print(np.transpose(A))
1
2

[[14 10 6]
[13 9 5]
[12 8 4]
[11 7 3]]

print(A.T)
1

[[14 10 6]
[13 9 5]
[12 8 4]
[11 7 3]]

4.3 多维数组的修建操作 clip

将原本数组中的数据范围修改成指定的数据范围，让所有数的取值都落入到自己指定的数据表示范围中去，不在指定范围内的数都会被强制修改为指定范围的最小值或者最大值。

• clip(Array,Array_min,Array_max)
  将Array_min<X<Array_max X表示矩阵A中的数，如果满足上述关系，则原数不变。否则，如果X<Array_min，则将矩阵中X变为Array_min；如果X>Array_max，则将矩阵中X变为Array_max

print(np.clip(A,5,9))
1

[[9 9 9 9]
[9 9 8 7]
[6 5 5 5]]

4.4 多维数组转一维 flatten

# 多维转一维
A = np.arange(3,15).reshape((3,4))
# print(A)
print(A.flatten())
# flat是一个迭代器，本身是一个object属性
1
2
3
4
5

[ 3 4 5 6 7 8 9 10 11 12 13 14]

4.5 其它操作

其他操作和一维数组中类似，只有在乘法这块上不一样，只有多维数组才能实现矩阵乘法操作。

5. 数组中的数据统计

5.1 三角函数 sin cos tan acr

np.sin、np.cos、np.tan、np.arcsin、np.arccos、np.arctan这些都可以使用，在numpy库中都可以找到对应的函数方法。

# Numpy中具有很多的数学函数工具
c = np.sin(a)
print(c)
1
2
3

5.2 最大值/最小值 max min

调用numpy中的内置方法min、max找到最值；

• 除了计算整体的最值以外，还可以计算沿着指定的轴的最值，只要我们在参数列表中为 axis 进行赋值。
  例如：
  当axis的值为0的时候，将会以列作为查找单元，
  当axis的值为1的时候，将会以行作为查找单元。

print(np.max(a))
print(np.min(a，axis=1))
1
2

5.3 最值索引 argmax argmin

除了可以找到数组中的最值，我们还可以找到数组中最值的索引。但返回的是在一维数组下的索引，即使是在多维数组中使用最值索引，返回的也是一维坐标，而不是多维坐标。

print(np.argmax(a))
print(np.argmin(a))
1
2

5.4 均值 mean average

以下三种方法效果类似，同时都可以沿着指定的轴进行计算均值。mean和average类似但是在源码上略有不同。

print(np.mean(a))
print(np.average(a)
print(a.mean())
1
2
3

5.5 总和 sum

# 累加
print(np.cumsum(a))
print(a.sum())
1
2
3

5.6 中位数 median

# 中位数
print(np.median(a))
1
2

5.7 方差和标准差 var std

print(a.var())
print(a.std())
1
2

5.8 开平方 sqrt

print(np.sqrt(a))
1

5.9 对数和指数运算 log power

对数运算不指定底数，默认以 $e$ 为底数。但我们也可以指定底数，但只能指定2或者10为底数。

print(np.log(a))
print(np.log2(a))
print(np.log10(a))
1
2
3

指数运算也可以直接用Python中的**进行指数运算，也可以用numpy中封装好的指数方法。

print(np.power(a,2))
1

5.10 绝对值 abs

将数组中的所有元素都以绝对值表示

print(np.abs(a))
1

5.11 排序 sort

对于多维数组的排序，只能在多维数组中的最小列表单位内部中排序。

# 仿照列表排序
A = np.arange(14,2,-1).reshape((3,4)) # -1表示反向递减一个步长
print(A)
1
2
3

[[14 13 12 11]
[10 9 8 7]
[ 6 5 4 3]]

print(np.sort(A))
1

[[11 12 13 14]
[ 7 8 9 10]
[ 3 4 5 6]]

---

6. 数组的索引和切片操作

Python中是可以对序列进行切片的，同样numpy中也提供了对数组的类切片操作，可以灵活根据指定的索引，取出我们所需的数组片段。

6.1 一维数组的索引

这个就是正常的用法,直接写数组下标就可以了

import numpy as np
A = np.arange(3,15)
print(A)
1
2
3

[ 3 4 5 6 7 8 9 10 11 12 13 14]

print(A[3])
1

6.2 多维数组的索引

B = A.reshape(3,4)
print(B)
1
2

[[ 3 4 5 6]
[ 7 8 9 10]
[11 12 13 14]]

• 一维索引

print(B[2])
1

[11 12 13 14]

• 二维索引两种写法都行，输出结果都一样，不过第二种写法在numpy中应用更多，更推荐使用

print(B[0][2])
print(B[0,2])
1
2

5
5

6.3 数组的切片

这里以矩阵举例，一维数组的切片做法和Python中的序列切片操作一样。

• 行索引里的:表示，从开头到结尾，Z[:,2]表示矩阵中的第二列元素，和Python序列中切片的:含义相同

Z = np.arange(9).reshape(3,3)
print( Z[:,2] )
1
2

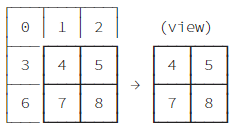
• Z[1:,1:]表示 行的取值范围是第一行到最后一行，列的取值范围是第一列到最后一列，最后行和列两个维度相重叠的部分，就是最后取到的数据

Z[1:,1:]
1

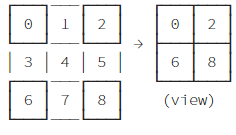
• 除了可以指定边界之外，还可以指定步长，[::2,::2]表示行的步长为2，列的步长也为2相重叠下的部分

Z[::2,::2]
1

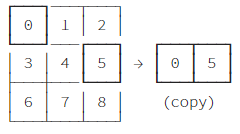
• 在指定的多维索引上下边界中，返回一个 1 * 维度数 的矩阵，内容是指定边界的开头结尾的元素（可能有点难理解，等我以后应用到了再回来补充）

Z[[0,1],[0,2]]
1

• 更为复杂的例子如下，反正方法很多很灵活，找到适合自己的一套方法就行了。

---

7. 数组的逻辑运算操作

7.1 逻辑运算

• 可以对数组中的每一个元素都进行逻辑比较判断运算，返回的是数组中每一个元素比较判断结果的布尔值True、False，我们可以直接对数组进行比较，具体例子如下：

a = np.array([1,1,4,3])
b = np.arange(4)
print(a==b)
1
2
3

[False True False True]

print(b<2)
1

[ True True False False]

7.2 条件查询

还可以通过写条件查询在使用索引访问数组时，这时就会返回一个列表表示条件查询的结果。例如：在一维数组中 取大于3 并且 可以被二整除 的元素

print(a[(a > 3)&(a % 2 == 0)])
1

8. 数组的合并

可以对要合并的方向上尺寸相同的数组进行合并

8.1 上下合并

A = np.array([1,1,1])
B = np.array([2,2,2])
print(np.vstack((A,B)))
# vertical stack 上下合并,对括号的两个整体操作。
1
2
3
4

[[1 1 1]
[2 2 2]]

8.2 左右合并

# horizontal stack左右合并
D = np.hstack((A,B))
print(D)
1
2
3

[1 1 1 2 2 2]

---

9. 广播 Broadcasting

numpy中独有的特性：广播Broadcasting
numpy数组间的基础运算是一对一，也就是a.shape==b.shape，但是当两者不一样的时候，就会自动触发广播机制。
不同尺寸的数组也可以直接做运算，在运算之前numpy会将两个数组扩展至相同的尺寸，然后再将相同位置的元素相加

from numpy import array
a = array([[ 0, 0, 0],
           [10,10,10],
           [20,20,20],
           [30,30,30]])
b = array([0,1,2])
print(a+b)
1
2
3
4
5
6
7

[[ 0 1 2]
[10 11 12]
[20 21 22]
[30 31 32]]

• 很明显当不同尺寸的数组做运算时，小的那个会扩展尺寸向大的那个靠拢，同时小数组新扩展出来的位置会用原本存在的元素填充。具体如下图。

• 但不是什么时候，两个大小不同的数组运算时都会触发广播。只有当两个数组的尾部维度相同时才能够进行相互运算trailing dimensions compatible，可以理解为矩阵进行乘法前的条件，否则会报错。

---

总结

一开始我以为挺简单的学这个Numpy库，结果我发现细节还是很多的，后面发现很灵活，没我想的那么简单。这篇我博客以为一晚上就能写完，结果花了我两天的时间在这上面。或者下次可以试试其他学习方法，这次一边学一边写博客，效率好像有点低，也可能我不太习惯。学习下一个库函数Scipy时，我看看要不要先手敲一边代码，再来考虑做笔记。

参考资料

1. Github上的入门教程numpy-beginner
2. 英文教程 From Python to Numpy