- 1AI科技,赋能企业财务管理
- 2(三) InnoDB笔记之查询(B+树索引)_b+树查询
- 3秒杀DeepLabv3+与UNet的表面缺陷检测网络
- 4《Git常用命令》详细讲解·第5篇(git log和git blame)_git blame csdn
- 5(一)大数据---Hadoop整体介绍(架构层)----(组件、引擎)分类_hadoop组层
- 6AI辅写疑似度检测软件:七个推荐工具助你识别高风险_ai检测软件
- 7AIGC大模型必备知识——LLM ,你知道它是如何训练的吗?小白必读深度好文_llm模型训练
- 8internal/modules/cjs/loader.js:968 throw err; ^ Error: Cannot find module ‘webpack-cli/bin/conf
- 9在树莓派下利用DS18B20传感器获取温度
- 10用python画颗爱心祝生日快乐_python如何实现生日快乐代码
DDPM Stable Diffusion_参数重整化
赞
踩
1、介绍
目前所采用的扩散模型大都是来自于2020年的工作DDPM: Denoising Diffusion Probabilistic Models,和GAN相比,DDPM拟合的是加噪图片,并通过反向过程(去噪)生成原始图片。而GAN通过判别器拟合原始图片,和DDPM有本质的区别。

图1 GAN和DDPM模型对比
图1中,GAN模型通过使得生成器(Generator)生成的图片 x′ 尽可能逼近真实图片 x ,从而达到以假乱真的目的,本质上还是去生成和真实图片接近的新图片,因此GAN生成的图片可能没有太多亮点。而DDPM是拟合整个从真实图片 x0 到随机高斯噪声 z 的过程,再通过反向过程生成新的图片,和GAN有本质的区别。
DDPM模型原理
DDPM包括两个过程:前向过程(forward process)和反向过程(reverse process),其中前向过程又称为扩散过程(diffusion process),如下图所示。无论是前向过程还是反向过程都是一个参数化的马尔可夫链(Markov chain),其中反向过程可以用来生成图片。

图2 DDPM前向和反向过程
图2中,由高斯随机噪声 xT 生成原始图片 x0 为反向过程,反之为前向过程。为了尽可能简化,我们主要介绍下前向过程、反向过程、DDPM如何训练、DDPM如何生成图片以及DDPM代码实现。
DDPM前向过程(扩散过程)
一句话概括,前向过程就是对原始图片 x0 不断加高斯噪声最后生成随机噪声 xT 的过程,如下图所示(图片来自于网络)。

图3 DDPM前向过程
由 xt−1 到 xt 可以表示为:
(1)xt=αtxt−1+1−αtϵt−1其中 αt 是一个很小值的超参数, ϵt−1∼N(0,1) 是高斯噪声。由公式(1)推导,最终可以得到 x0 到 xt 的公式,表示如下:
(2)xt=α¯tx0+1−α¯tϵ其中 α¯t=∏i=1tαi ,ϵ∼N(0,1) 也是一个高斯噪声。有了公式(2),便可以由输入图片x0直接生成随机噪声。
DDPM反向过程(去燥过程)
前向过程是将原始图片变成随机噪声,而反向过程就是通过预测噪声 ϵ ,将随机噪声 xT 逐步还原为原始图片 x0 ,如下图所示。

图4 DDPM反向过程
反向过程公式表示如下:
(3)xt−1=1αt(xt−1−αt1−α¯tϵθ(xt,t))+σtz其中 ϵθ 是噪声估计函数(一般使用NN模型),用于估计真实噪声 ϵ , θ 是模型训练的参数, z∼N(0,1) , σtz 表示的是预测噪声和真实噪声的误差。DDPM的关键就是训练噪声估计模型 ϵθ(xt,t) ,用于估计真实的噪声 ϵ。
DDPM如何训练
前面提到DDPM的关键是训练噪声估计模型 ϵθ(xt,t) ,用于估计 ϵ ,那么损失函数可以使用MSE误差,表示如下:
(4)Loss=‖ϵ−ϵθ(xt,t)‖2=‖ϵ−ϵθ(α¯txt−1+1−α¯tϵ,t)‖2整个训练过程可以表示如下:

图5 DDPM训练过程
论文中的DDPM训练过程如下所示:

图6 论文中DDPM训练过程
DDPM如何生成图片
在得到预估噪声 ϵθ(xt,t) 后,就可以按公式(3)逐步得到最终的图片 x0 ,整个过程表示如下:

图7 DDPM生成图片过程
2、公式推导
前置知识
① 贝叶斯法则
先验概率 P(θ) :根据以往的经验和分析得到的,假设 θ 发生的概率;
似然函数 P(x∣θ) :在假设 θ 已发生的前提下,发生事件 x 的概率;
后验概率 P(θ∣x) :在事件 x 已发生的前提下,假设 θ 成立的概率;
标准化常量 P(x) :在已知所有假设下,事件 x 发生的概率;
它们之间的关系为: P(θ∣x)=P(x∣θ)P(θ)P(x)
② 贝叶斯公式
P(A,B)=P(B∣A)P(A)=P(A∣B)P(B)
P(A,B,C)=P(C∣B,A)P(B,A)=P(C∣B,A)P(B∣A)P(A)
P(B,C∣A)=P(B∣A)P(C∣A,B)
若满足马尔科夫链关系 A→B→C ,即当前时刻的概率分布仅与上一时刻有关,则有:
P(A,B,C)=P(C∣B,A)P(B,A)=P(C∣B)P(B∣A)P(A)
P(B,C∣A)=P(B∣A)P(C∣B)
③ 高斯分布的概率密度函数、高斯函数的叠加公式
给定均值为 μ ,方差为 σ2 的单一变量高斯分布 N(μ,σ2) ,其概率密度函数为:
q(x)=12πσexp(−12(x−μσ)2) 很多时候,为了方便起见,可以将前面的常数系数去掉,写成:
q(x)∝exp(−12(x−μσ)2) ⇔ q(x)∝exp(−12(1σ2x2−2μσ2x+μ2σ2)) 给定两个高斯分布 X∼N(μ1,σ12) , Y∼N(μ2,σ22) ,则它们叠加后的 aX+bY 满足:
aX+bY∼N(a×μ1+b×μ2,a2×σ12+b2×σ22)
④ KL散度
KL散度可以用来衡量两个分布的差异,假设随机变量的真实概率分布为 P ,而我们通过建模得到的一个近似分布为 Q ,则 P 与 Q 的KL散度满足下式:
DKL(P,Q)=−∑PlogQ−(−∑PlogP)=∑PlogPQ
对于两个单一变量的高斯分布 p∼N(μ1,σ12) 和 q∼N(μ2,σ22) 而言,它们的KL散度为:
DKL(p,q)=logσ2σ1+σ12+(μ1−μ2)22σ22−12
⑤ 参数重整化(重参数技巧)
若要从高斯分布 N(μ,σ2) 中采样,可先从标准分布 N(0,1) 中采样出 z ,再得到 σ2∗z+μ ,即我们的采样值。这样做的目的是将随机性转移到 z 上,让采样值对 μ 和 σ 可导。
基本介绍
如下图所示,DDPM模型主要分为两个过程:加噪过程(从右往左)和去噪过程(从左往右)。
★ 加噪过程:给定真实图像 x0 ,逐步对它添加高斯噪声,得到 x1, x2, ⋯ ,显然这是一个马尔科夫链过程,在进行了足够多的 T 次加噪后,图像会被高斯噪声淹没,可以认为是各向独立的高斯噪声的图像。
★ 去噪过程:针对噪声图像 xT ,让神经网络模型对其逐步去噪,得到 xT−1, xT−2, ⋯ ,最终复原出没有噪声的逼真图像 x0 ,所以加噪过程其实可以看作是在为去噪过程构建标签。

前向过程(扩散过程,加噪过程)
给定初始图像 x0 ,向其中逐步添加高斯噪声,加噪过程持续 T 次,产生一系列带噪图像,达到破坏图像的目的。由 xt−1 加噪至 xt 的过程中,所加噪声的方差为 βt ,又称扩散率,是一个给定的,大于 0 小于 1 的,随扩散步数增加而逐渐增大的值。定义扩散过程如下式:
xt=1−βtxt−1+βtzt,zt∼N(0,I)
根据定义,加噪过程可以看作在上一步的基础上乘了一个系数,然后加上均值为 0 ,方差为 βt 的高斯分布。所以加噪过程是确定的,并不是可学习的过程,将其写成概率分布的形式,则有:
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)
此外,加噪过程是一个马尔科夫链过程,所以联合概率分布可以写成下式:
q(x1,x2,⋯,xT|x0)=q(x1|x0)q(x2|x1)⋯q(xT|xT−1)=∏t=1Tq(xt|xt−1)
定义 αt=1−βt ,即 αt+βt=1 ,代入 xt 表达式并迭代推导,可得 x0 到 xt 的公式:
xt=1−βtxt−1+βtzt=αtxt−1+βtzt
=αt(αt−1xt−2+βt−1zt−1)+βtzt
=αtαt−1xt−2+αtβt−1zt−1+βtzt
=αtαt−1(αt−2xt−3+βt−2zt−2)+αtβt−1zt−1+βtzt
=αtαt−1αt−2xt−3+αtαt−1βt−2zt−2+αtβt−1zt−1+βtzt
=αtαt−1⋯α1x0+αtαt−1⋯α2β1z1+αtαt−1⋯α3β2z2+⋯+αtαt−1βt−2zt−2+αtβt−1zt−1+βtzt
上式从第二项到最后一项都是独立的高斯噪声,它们的均值都为0,方差为各自系数的平方。根据高斯分布的叠加公式,它们的和满足均值为0,方差为各项方差之和的高斯分布。又有上式每一项系数的平方和(包括第一项)为1,证明如下,注意始终有 αt+βt=1 :
αtαt−1⋯α1+αtαt−1⋯α2β1+αtαt−1⋯α3β2+⋯+αtβt−1+βt
=αtαt−1⋯α2(α1+β1)+αtαt−1⋯α3β2+⋯+αtαt−1βt−2+αtβt−1+βt
=αtαt−1⋯α2×1+αtαt−1⋯α3β2+⋯+αtαt−1βt−2+αtβt−1+βt
=αtαt−1⋯α3(α2+β2)+⋯+αtαt−1βt−2+αtβt−1+βt
=αtαt−1⋯α3×1+⋯+αtαt−1βt−2+αtβt−1+βt
=⋯⋯=αt+βt=1
那么,将 αtαt−1⋯α1 记作 α¯t ,则正态噪声的方差之和为 1−α¯t , xt 可表示为:
xt=α¯tx0+1−α¯tz¯t,z¯t∼N(0,I)
由该式可以看出, xt 实际上是原始图像 x0 和随机噪声 z¯t 的线性组合,即只要给定初始值,以及每一步的扩散率,就可以得到任意时刻的 xt ,写成概率分布的形式:
q(xt∣x0)=N(xt;α¯tx0,(1−α¯t)I)
当加噪步数 T 足够大时, α¯t 趋向于 0, 1−α¯t 趋向于 1,所以 xT 趋向于标准高斯分布。
反向过程(逆扩散过程,去噪过程)
前向过程对原始图像 x0 逐步加噪声变成 xT ,反向过程则是从 xT 逐步恢复到 x0 。前向过程用 q(xt∣xt−1) 来表示,那么反向过程则是求 q(xt−1∣xt) 。如果能实现这种逆转,就可以从一个随机的高斯噪声 N(0,I) 中重建出一个真实的原始样本,实现图像生成的目的。
有文献证明,如果 q(xt∣xt−1) 满足高斯分布且扩散率 βt 足够小,则 q(xt∣xt−1) 也满足高斯分布。虽然前向过程中每一步所加的噪声都采样自特定的高斯分布,但是采样有无数种可能性,所以 q(xt−1∣xt) 不太可能从理论上求得,我们可以通过学习一个深度网络(参数为 θ )来拟合。
反向过程仍然是一个马尔科夫链过程,网络以当前时刻 t 和当前时刻的状态 xt 作为输入,构建反向过程条件概率,其中,均值和方差都是含参的,且都以 xt 和 t 作为输入,有下式:
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))
pθ(x0:T)=pθ(xT)pθ(xT−1∣xT)⋯pθ(x0∣x1)=pθ(xT)∏t=1Tpθ(xt−1∣xt)
而真实的反向过程,或者称作扩散过程的后验条件概率,根据贝叶斯公式可以写成:
q(xt−1∣xt)=q(xt∣xt−1)q(xt−1)q(xt)
其中, q(xt−1) 是不可知的,但是如果知道 x0 ,则扩散过程的后验条件概率可以写成:
q(xt−1∣xt,x0)=q(xt∣xt−1,x0)×q(xt−1∣x0)q(xt∣x0)=N(xt−1,μ~(xt,x0),β~tI)
又根据前向过程的推导,有下面三个式子满足:
q(xt−1|x0)=α¯t−1x0+1−α¯t−1z¯t−1∼N(xt−1;α¯t−1x0,(1−α¯t−1)I)
q(xt∣x0)=α¯tx0+1−α¯tz¯t∼N(xt;α¯tx0,(1−α¯t)I)
q(xt∣xt−1,x0)=q(xt∣xt−1)=αtxt−1+βtzt∼N(xt;αtxt−1,βtI)
将三个式子代入,并结合前置知识中的高斯函数概率密度函数,展开后合并同类项,有下式:
q(xt−1∣xt,x0)=N(xt;αtxt−1,βtI)×N(xt−1;α¯t−1x0,(1−α¯t−1)I)N(xt;α¯tx0,(1−α¯t)I)
∝exp(−12((xt−αtxt−1)2βt+(xt−1−α¯t−1x0)21−α¯t−1−(xt−α¯tx0)21−α¯t))
=exp(−12(xt2−2αtxtxt−1+αtxt−12βt+xt−12−2α¯t−1x0xt−1+α¯t−1x021−α¯t−1−(xt−α¯tx0)21−α¯t))
=exp(−12((αtβt+11−α¯t−1)xt−12−(2αtβtxt+2α¯t−11−α¯t−1x0)xt−1+C(xt,x0)))
此式符合前置知识中高斯函数概率密度函数的展开形式,有以下两个式子满足:
1βt~2=αtβt+11−α¯t−1and2μ~(xt,x0)βt~2=2αtβtxt+2α¯t−11−α¯t−1x0
对第一个式子,有:
1βt~2=αt(1−α¯t−1)+βtβt(1−α¯t−1)=αt−αtα¯t−1+1−αtβt(1−α¯t−1)=1−α¯tβt(1−α¯t−1)
对第二个式子,有:
μ~(xt,x0)=(αtβtxt+α¯t−11−α¯t−1x0)×βt~2=(αtβtxt+α¯t−11−α¯t−1x0)×1−α¯t−11−α¯tβt
=αt(1−α¯t−1)1−α¯txt+α¯t−11−α¯tβtx0=αt(1−α¯t−1)1−α¯txt+α¯t−11−α¯tβtxt−1−α¯tz¯tα¯t
=(αt(1−α¯t−1)1−α¯t+βtα¯t−1α¯t(1−α¯t))xt−α¯t−11−α¯tβtz¯tα¯t(1−α¯t)
=(αt(1−α¯t−1)1−α¯t+1−αtαt(1−α¯t))xt−βtz¯tαt1−α¯t
=αt(1−α¯t−1)+1−αtαt(1−α¯t)xt−βtz¯tαt1−α¯t=1−αtα¯t−1αt(1−α¯t)xt−βtz¯tαt1−α¯t
=1−α¯tαt(1−α¯t)xt−βtz¯tαt1−α¯t=1αt(xt−βt1−α¯tz¯t)
所以,在给定 x0 的条件下,反向过程真实的概率分布的均值只与 xt 和 z¯t 有关,满足下式:
q(xt−1∣xt,x0)=N(xt−1,μ~(xt,x0),β~tI)=N(xt−1,1αt(xt−βt1−α¯tz¯t),1−α¯t−11−α¯tβtI)
优化目标
扩散模型的目标是得到尽可能真实的 x0 ,即求模型参数 θ ,使其最终得到 x0 的概率最大,这显然是一个极大似然估计问题,写出似然函数:
p(x0∣θ)=pθ(x0)=∫x1∫x2⋯∫xTpθ(x0,x1,x2,⋯,xT)dx1dx2⋯dxT
=∫x1∫x2⋯∫xTq(x1:T∣x0)pθ(x0,x1,x2,⋯,xT)q(x1:T∣x0)dx1dx2⋯dxT=Eq(x1:T∣x0)[pθ(x0:T)q(x1:T∣x0)]
由 Jensen 不等式,对任一凸函数 f ,始终满足函数值的期望大于等于期望的函数值,对上式两边取负对数,得到负对数似然函数,满足:
−logpθ(x0)=−logEq(x1:T∣x0)[pθ(x0:T)q(x1:T∣x0)]≤Eq(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)]
式子右侧称为变分下界,最小化负对数似然函数可以转换为最小化变分下界,结合马尔科夫链的贝叶斯公式将变分下界展开:
LVLB=Eq(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)]
=Eq(x1:T∣x0)[logq(x1∣x0)q(x2∣x1)⋯q(xT∣xT−1)pθ(xT)pθ(xT−1∣xT)⋯pθ(x1∣x0)]
=Eq(x1:T∣x0)[log∏t=1Tq(xt∣xt−1)pθ(xT)∏t=1Tpθ(xt−1∣xt)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=1Tlogq(xt∣xt−1)pθ(xt−1∣xt)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt∣xt−1)pθ(xt−1∣xt)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt∣xt−1,x0)pθ(xt−1∣xt)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt,xt−1,x0)pθ(xt−1∣xt)q(xt−1,x0)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt−1∣xt,x0)q(xt∣x0)q(x0)pθ(xt−1∣xt)q(xt−1∣x0)q(x0)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)⋅q(xt∣x0)q(xt−1∣x0)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)+∑t=2Tlogq(xt∣x0)q(xt−1∣x0)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[−logpθ(xT)+∑t=2Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)+logq(xT∣x0)q(x1∣x0)+logq(x1∣x0)pθ(x0∣x1)]
=Eq(x1:T∣x0)[logq(xT∣x0)pθ(xT)+∑t=2Tlogq(xt−1∣xt,x0)pθ(xt−1∣xt)−logpθ(x0∣x1)]
因为和的期望等于期望的和,可得:
=Eq(x1:T∣x0)[logq(xT∣x0)pθ(xT)]+∑t=2TEq(x1:T∣x0)[logq(xt−1∣xt,x0)pθ(xt−1∣xt)]−Eq(x1:T∣x0)[logpθ(x0∣x1)]
因为期望目标与部分时间步的概率无关可以直接省去,可得:
=Eq(xT∣x0)[logq(xT∣x0)pθ(xT)]+∑t=2TEq(xt,xt−1∣x0)[logq(xt−1∣xt,x0)pθ(xt−1∣xt)]−Eq(x1∣x0)[logpθ(x0∣x1)]
中间的求和项根据前置知识中的贝叶斯公式改写,可得:
=Eq(xT∣x0)[logq(xT∣x0)pθ(xT)]+∑t=2TEq(xt∣x0)q(xt−1∣xt,x0)[logq(xt−1∣xt,x0)pθ(xt−1∣xt)]−Eq(x1∣x0)[logpθ(x0∣x1)]
=DKL(q(xT|x0)∥pθ(xT))+∑t=2TEq(xt∣x0)[DKL(q(xt−1|xt,x0)∥pθ(xt−1|xt))]−Eq(x1∣x0)[logpθ(x0|x1)]
=LT+LT−1+⋯+L0
对 LT 而言,先验分布 q(xT∣x0) 是确定的值,而 pθ(xT) 是一个各向同性的高斯分布,二者都不含参数,我们可将这一项视为常数,最小化变分上界时不用考虑。
对剩余的求和项,当 t 的取值为 1 时,分子为 q(x0∣x1,x0) ,即在已知 x0 的条件下求 x0 的概率分布,也是确定值,所以其实 L0 可以并入 Lt−1 ,由此可将变分上界简化一些。
推导到这里,优化目标就被转化为了最小化后验分布与网络参数化的高斯分布之间的KL散度。
为了简化计算,DDPM对 pθ(xt−1∣xt) 做了进一步简化,采用固定方差 Σθ(xt,t)=σt2I ,这里的 σt2 是一个无需训练的常量,文中提到,设置为 βt 或 β~t 有相似的效果,这里我们假定 σt2=β~t ,则KL散度中的两项分别可写作:
q(xt−1∣xt,x0)=N(xt−1,μ~(xt,x0),β~tI)=N(xt−1,μ~(xt,x0),σt2I)
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))=N(xt−1;μθ(xt,t),σt2I)
结合前置知识中高斯分布的KL散度公式,有:
DKL(q(xT|x0)∥pθ(xT))
=DKL(N(xt−1,μ~(xt,x0),σt2I)∥N(xt−1;μθ(xt,t),σt2I))
=log1+σt2+‖μ~t(xt,x0)−μθ(xt,t)‖22σt2−12
=12σt2‖μ~t(xt,x0)−μθ(xt,t)‖2
将此式代回之前变分上界的式子,则优化目标 Lt−1 可以写作:
Lt−1=Eq(xt∣x0)[12σt2‖μ~t(xt,x0)−μθ(xt,t)‖2]
也就是说,我们希望网络参数化高斯分布的均值 μθ(xt,t) 与后验分布的均值 μ~t(xt,x0) 一致。
此式还可以继续扩展,在反向过程中, μ~t(xt,x0) 可以写成用 xt 和 z¯t 表示的形式,而在前向过程中, xt 又可以写成用 x0 和 z¯t 表示的形式,将它们代入上式,则有:
Lt−1=Ex0,z¯t∼N(0,I)[12σt2‖1αt(xt(x0,z¯t)−βt1−α¯tz¯t)−μθ(xt(x0,z¯t),t)‖2]
其中,参数化高斯分布的均值 μθ(xt,t) 可以相应改写成与真实均值 μ~t(xt,x0) 一样的形式:
μθ(xt(x0,z¯t),t)=1αt(xt(x0,z¯t)−βt1−α¯tzθ(xt(x0,z¯t),t))
这里的 zθ(xt(x0,z¯t),t)) 是神经网络的拟合项,即优化目标由原来的拟合均值转换成了拟合噪声。将其代入 Lt−1 的表达式中,则 Lt−1 可表达为:
=Ex0,z¯t∼N(0,I)[12σt2‖1αt(xt(x0,z¯t)−βt1−α¯tz¯t)−1αt(xt−βt1−α¯tzθ(xt(x0,z¯t),t))‖2]
=Ex0,z¯t∼N(0,I)[12σt2‖xt(x0,z¯t)αt−βtαt1−α¯tz¯t−xt(x0,z¯t)αt+βtαt1−α¯tzθ(xt(x0,z¯t),t)‖2]
=Ex0,z¯t∼N(0,I)[12σt2‖βtαt1−α¯t(z¯t−zθ(xt(x0,z¯t),t))‖2]
=Ex0,z¯t∼N(0,I)[βt22σ2αt(1−α¯t)‖z¯t−zθ(α¯tx0+1−α¯tz¯t,t)‖2]
可以将系数项去掉,进一步简化:
Lt−1simple=Ex0,z¯t∼N(0,I)[‖z¯t−zθ(α¯tx0+1−α¯tz¯t,t)‖2]
虽然推导比较复杂,但最终得到的优化目标非常简单,就是让网络预测的噪声与真实的噪声一致。
3、Stable Diffusion
1. Diffusion文字生成图片——整体结构
1.1 整个生成过程
我们知道在使用 Diffusion 的时候,是通过文字生成图片,但是上一篇文章中讲的Diffusion模型输入只有随机高斯噪声和time step。那么文字是怎么转换成Diffusion的输入的呢?加入文字后 Diffusion 又有哪些改变?下图可以找到答案。

文字生成图片全过程
实际上 Diffusion 是使用Text Encoder生成文字对应的embedding(Text Encoder使用CLIP模型),然后和随机噪声embedding,time step embedding一起作为Diffusion的输入,最后生成理想的图片。我们看一下完整的图:

token embedding、随机噪声embedding、time embedding一起输入diffusion
上图我们看到了Diffusion的输入为token embedding和随机embedding,time embedding没有画出来。中间的Image Information Creator是由多个UNet模型组成,更详细的图如下:

更详细的结构
可以看到中间的Image Information Creator是由多个UNet组合而成的,关于UNet的结构我们放在后面来讲。
现在我们了解了加入文字embedding后 Diffusion 的结构,那么文字的embedding是如何生成的?接下来我们介绍下如何使用CLIP模型生成文字embedding。
1.2 使用CLIP模型生成输入文字embedding
CLIP 在图像及其描述的数据集上进行训练。想象一个看起来像这样的数据集,包含4 亿张图片及其说明:

图像及其文字说明
实际上CLIP是根据从网络上抓取的图像及其文字说明进行训练的。CLIP 是图像编码器和文本编码器的组合,它的训练过程可以简化为给图片加上文字说明。首先分别使用图像和文本编码器对它们进行编码。

然后使用余弦相似度刻画是否匹配。最开始训练时,相似度会很低。

然后计算loss,更新模型参数,得到新的图片embedding和文字embedding

通过在训练集上训练模型,最终得到文字的embedding和图片的embedding。有关CLIP模型的细节,可以参考对应的论文。
1.3 UNet网络中如何使用文字embedding
前面已经介绍了如何生成输入文字embedding,那么UNet网络又是如何使用的?实际上是在UNet的每个ResNet之间添加一个Attention,而Attention一端的输入便是文字embedding。如下图所示。

更详细的图如下:

2. 扩散模型Diffusion
前面介绍了Diffusion是如何根据输入文字生成图片的,让大家有个大概的了解,接下来会详细介绍扩散模型Diffusion是如何训练的,又是如何生成图片的。
2.1 扩散模型Duffison的训练过程

扩散模型Diffusion
Diffusion模型的训练可以分为两个部分:
- 前向扩散过程(Forward Diffusion Process) → 图片中添加噪声
- 反向扩散过程(Reverse Diffusion Process) → 去除图片中的噪声
2.2 前向扩散过程
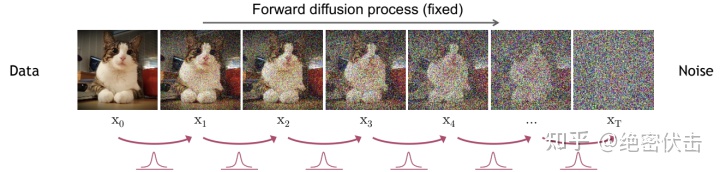
前向扩散过程是不断往输入图片中添加高斯噪声。
2.3 反向扩散过程

反向扩散过程是将噪声不断还原为原始图片。
2.4 训练过程

在每一轮的训练过程中,包含以下内容:
- 每一个训练样本选择一个随机时间步长 t
- 将time step t 对应的高斯噪声应用到图片中
- 将time step转化为对应embedding
下面是每一轮详细的训练过程:

2.5 从高斯噪声中生成原始图片(反向扩散过程)

上图的Sample a Gaussian表示生成随机高斯噪声,Iteratively denoise the image表示反向扩散过程,如何一步步从高斯噪声变成输出图片。可以看到最终生成的Denoised image非常清晰。
补充1:UNet模型结构
前面已经介绍了Diffusion的整个过程,这里补充以下UNet的模型结构,如下图所示

这里面Downsampe、Middle block、Upsample中都包含了ResNet残差网络。
补充2:Diffusion模型的缺点及改进版——Stable Diffusion
前面我们在介绍整个文字生成图片的架构中,图里面用的都是Stable Diffusion,后面介绍又主要介绍的是Diffusion。其实Stable Diffusion是Diffusion的改进版。
Diffusion的缺点是在反向扩散过程中需要把完整尺寸的图片输入到U-Net,这使得当图片尺寸以及time step t足够大时,Diffusion会非常的慢。Stable Diffusion就是为了解决这一问题而提出的。后面有时间再介绍下Stable Diffusion是如何改进的。
补充3:UNet网络同时输入文字embedding
在第2节介绍Diffusion原理的时候,为了方便,都是没有把输入文字embedding加进来,只用了time embedding和随机高斯噪声,怎么把文字embedding也加进来可以参考前面的1.3节。
补充4:DDPM为什么要引入时间步长t
引入时间步长 t 是为了模拟一个随时间逐渐增强的扰动过程。每个时间步长 t 代表一个扰动过程,从初始状态开始,通过多次应用噪声来逐渐改变图像的分布。因此,较小的 t 代表较弱的噪声扰动,而较大的 t 代表更强的噪声扰动。
这里还有一个原因,DDPM 中的 UNet 都是共享参数的,那如何根据不同的输入生成不同的输出,最后从一个完全的一个随机噪声变成一个有意义的图片,这还是一个非常难的问题。我们希望这个 UNet 模型在刚开始的反向过程之中,它可以先生成一些物体的大体轮廓,随着扩散模型一点一点往前走,然后到最后快生成逼真图像的时候,这时候希望它学习到高频的一些特征信息。由于 UNet 都是共享参数,这时候就需要 time embedding 去提醒这个模型,我们现在走到哪一步了,现在输出是想要粗糙一点的,还是细致一点的。
所以加入时间步长 t 对生成和采样过程都有帮助。
补充5:为什么训练过程中每一次引入的是随机时间步长 t
我们知道模型在训练过程中 loss 会逐渐降低,越到后面 loss 的变化幅度越小。如果时间步长 t 是递增的,那么必然会使得模型过多的关注较早的时间步长(因为早期 loss 大),而忽略了较晚的时间步长信息。
3.1 另外一版
写在最前面:
由于Stable Diffusion里面有关扩散过程的描述,描述方法有很多版本,比如前向过程也可以叫加噪过程,为了便于理解,这里把各种描述统一说明一下。
- Diffusion扩散模型:文章里面所有出现Diffusion扩散模型的地方,都是指2020年提出的DDPM模型DDPM: Denoising Diffusion Probabilistic Models
- 前向扩散过程、加噪过程(含义一样,下同)
- 反向扩散过程、去噪过程、图片生成过程、Sampling
- 单轮去噪过程、单轮U-Net过程、单轮反向扩散过程
开源的Stable Diffusion
目前AI绘画最火的当属Midjorney和Stable Diffusion,但是由于Midjourney没有开源,因此我们主要分享下Stable Diffusion,后面我们会补充介绍下Midjourney。
公开资料显示,Stable Diffusion是StabilityAI公司于2022年提出的,论文和代码都已开源。StabilityAI在10月28日完成了1.01亿美元的融资,目前估值已经超过10亿美元。
大家可以去Stable Diffusion Online这个网站体验一下Stable Diffusion,我们输入文本“’A sunset over a mountain range, vector image”(山脉上的日落),看一下效果:

Stable Diffusion绘画
在了解应用后,接下来我们介绍下Stable Diffusion。主要还是通过图解的方式,避免大量公式推导,看起来费劲。
1. Stable Diffusion文字生成图片过程
Stable Diffusion其实是Diffusion的改进版本,主要是为了解决Diffusion的速度问题。那么Stable Diffusion是如何根据文字得出图片的呢?下图是Stable Diffusion生成图片的具体过程:

Stable Diffusion文字生成图片过程
可以看到,对于输入的文字(图中的“An astronout riding a horse”)会经过一个CLIP模型转化为text embedding,然后和初始图像(初始化使用随机高斯噪声Gaussian Noise)一起输入去噪模块(也就是图中Text conditioned latent U-Net),最后输出 512×512 大小的图片。在文章(绝密伏击:十分钟读懂Diffusion:图解Diffusion扩散模型)中,我们已经知道了CLIP模型和U-Net模型的大致原理,这里面关键是Text conditioned latent U-net,翻译过来就是文本条件隐U-net网络,其实是通过对U-Net引入多头Attention机制,使得输入文本和图像相关联,后面我们重点讲讲这一块是怎么做的。
2. Stable Diffusion的改进一:图像压缩
Stable Diffusion原来的名字叫“Latent Diffusion Model”(LDM),很明显就是扩散过程发生隐空间中(latent space),其实就是对图片做了压缩,这也是Stable Diffusion比Diffusion速度快的原因。
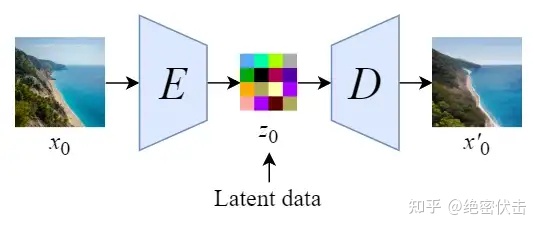
自编码器(Autoencoder)
Stable Diffusion会先训练一个自编码器,来学习将图像压缩成低维表示。
- 通过训练好的编码器 E ,可以将原始大小的图像压缩成低维的latent data(图像压缩)
- 通过训练好的解码器 D ,可以将latent data还原为原始大小的图像
在将图像压缩成latent data后,便可以在latent space中完成扩散过程,对比下和Diffusion扩散过程的区别,如下图所示:

Diffusion扩散过程和Stable Diffusion扩散过程的对比
可以看到Diffusion扩散模型就是在原图 x 上进行的操作,而Stale Diffusion是在压缩后的图像 z 上进行操作。
Stable Diffusion的前向扩散过程和Diffusion扩散模型基本没啥区别,只是多了一个图像压缩,只是反向扩散过程二者之前还是有区别。
3. Stable Diffusion的改进二:反向扩散过程
在第一节我们已经简单介绍过Stable Diffusion文字生成图片的过程,这里我们扩展下,看一下里面的细节,如下图所示:
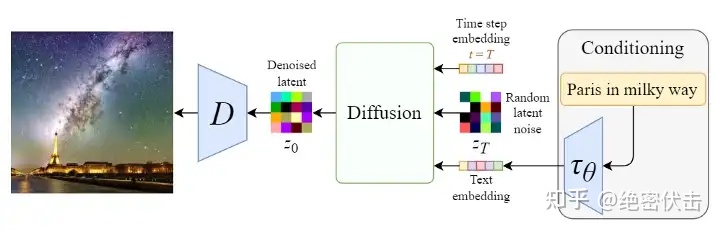
支持文本输入的反向扩散过程
上图从右至左,输入的文字是“Pairs in milky way”(银河系的巴黎),经过CLIP模型 τθ 转为Text embedding,然后和初始图像(噪声向量 zT )、Time step向量 T ,一起输入Diffusion模块(多轮去噪过程),最后将输出的图像 z0 经过解码器 D 后,生成最终的图像。
Stable Diffusion在反向扩散过程中其实谈不上改进,只是支持了文本的输入,对U-Net的结构做了修改,使得每一轮去噪过程中文本和图像相关联。在上一篇文章(绝密伏击:十分钟读懂Diffusion:图解Diffusion扩散模型)中,我们在介绍使用Diffusion扩散模型生成图像时,一开始就已经介绍了在扩散过程中如何支持文本输入,以及如何修改U-Net结构,只是介绍U-Net结构改进的时候,讲的比较粗,感兴趣的可以去看看里面的第一节。下面我们就补充介绍下Stable Diffusion是如何对U-Net结构做修改,从而更好的处理输入文本。
3.1 反向扩散细节:单轮去噪U-Net引入多头Attention(改进U-Net结构)
我们先看一下反向扩散的整体结构,如下图所示:
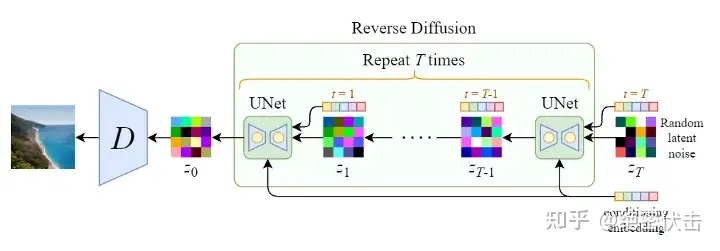
反向扩散过程的整体结构
从上图可以看出,反向扩散过程中输入文本和初始图像 ZT 需要经过 T 轮的U-Net网络( T 轮去噪过程),最后得到输出 Z0 ,解码后便可以得到最终图像。由于要处理文本向量,因此必然要对U-Net网络进行调整,这样才能使得文本和图像相关联。下图是单轮的去噪过程:

单轮去噪过程
上图的最左边里面的Semantic Map、Text、Representations、Images稍微不好理解,这是Stable Diffusion处理不同任务的通用框架:
- Semantic Map:表示处理的是通过语义生成图像的任务
- Text:表示的就是文字生成图像的任务
- Representations:表示的是通过语言描述生成图像
- Images:表示的是根据图像生成图像
这里我们只考虑输入是Text,因此首先会通过模型CLIP模型生成文本向量,然后输入到U-Net网络中的多头Attention(Q, K, V)。
这里补充一下多头Attention(Q, K, V)是怎么工作的,我们就以右边的第一个Attention(Q, K, V)为例。
(1)Attention(Q,K,V)=softmax(QKTd)⋅V其中: Q=WQ⋅zT,K=WK⋅τθ(y),V=WV⋅τθ(y) 。可以看到每一轮去噪过程中,文本向量 τθ(y) 会和当前图像 zT 计算相关性。
Stable Diffusion完整结构
最后我们来看一下Stable Diffusion完整结构,包含文本向量表示、初始图像(随机高斯噪声)、时间embedding,如下图所示:

Stable Diffusion完整结构
上图详细的展示了Stable Diffusion前向扩散和反向扩散的整个过程,我们再看一下不处理输入文字,只是单纯生成任意图像的Diffusion结构。

不输入文字,单纯生成任意图像的Diffusion结构
可以看到,不处理文字输入,生成任意图像的Diffusion模型,和Stable Diffusion相比,主要有两个地方不一样:
- 少了对输入文字的embedding过程(少了编码器 E、解码器 D )
- U-Net网络少了多头Attention结构
4 其他参考
HuggingFace推荐的博客:
代码+公式:The Annotated Diffusion Model
知乎讨论:diffusion model 最近在图像生成领域大红大紫,如何看待它的风头开始超过 GAN ? - 知乎
B站视频:


