【BFS】八数码问题（c++基础算法）_八数码问题例题

目录

一.读题

二.在做题之前

1.康拓展开

2.DFS和BFS的区别

3.栈和队列的区别

三.做题

1.算法原理

2.算法实现

①队列

②康托展开

 ③标记

四.AC代码

---

一.读题

作为最经典的一道宽度优先搜索题，它的题面并不是很难懂。

【宽搜（难度：6）】8数码问题

题目描述

【题意】 
  

在3×3的棋盘上摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围上下左右相邻的棋子可以移到空格中。

现给出原始状态和目标状态，求实现从初始布局到目标布局的最少步骤（初始状态的步数为0）。

如下图，答案为5。 

  

 
【输入格式】
    第一个3*3的矩阵是原始状态；
    第二个3*3的矩阵是目标状态。
【输出格式】
    输出移动所用最少的步数。
【样例1输入】
2 8 3
1 6 4
7 0 5
1 2 3
8 0 4
7 6 5
【样例1输出】
5
 
【样例2输入】
2 8 3
1 6 4
7 0 5
0 1 2
3 4 5
8 7 6
【样例2输出】
17

很显然，这是要我们求出矩阵1通过白色方块的上下左右移动转化向矩阵2的最小步数。

---

二.在做题之前

在做题之前，我们先要弄懂3个问题。

1.康拓展开

在这道题中，我们要利用康托展开判断是否重复。在文前，蒟蒻已经写了一篇文章，不懂的可以去看一下：【宽搜必备】康托展开（从公式解析到代码实现）

那么，我们就可以写出：

int kt(int a[],int n)
{
	int s=1;
	for(int i=1;i<=n;i++)
	{
		int index=1,f=1,count=0;
		for(int j=i+1;j<=n;j++)
		{
			f*=index;
			index++;
			if(a[i]>a[j]) count++; 
		}
		s=s+count*f;
	}	
	return s;
} 

2.DFS和BFS的区别

bfs 遍历节点是先进先出，dfs遍历节点是先进后出；
bfs是按层次访问的，dfs 是按照一个路径一直访问到底，当前节点没有未访问的邻居节点时，然后回溯到上一个节点，不断的尝试，直到访问到目标节点或所有节点都已访问。
bfs 适用于求源点与目标节点距离最近的情况，例如：求最短路径。dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况，例如：全排列、拓扑排序、求到达某一点的任意一条路径。

3.栈和队列的区别

（1）栈和队列的出入方式不同：栈是后进先出、队列是先进先出。
（2）栈和队列在具体实现的时候操作的位置不同：因为栈是后进先出，它在一段进行操作；而队列是先进先出，实现的时候在两端进行。

现在，我们搞懂了这三个问题，就可以做题了。

---

三.做题

1.算法原理

采用BFS遍历的方式寻找最优路径。

首先定义一个结构体ma来存放八数码的每一个状态信息，其中包括节点对应的矩阵，节点在BFS遍历树中的深度（相当于步数），以及节点对应的康托值。然后，定义visited数组存放已经访问过的节点状态。

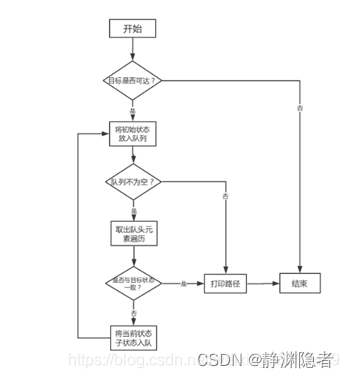
利用队列实现遍历，具体步骤如下:

1.将初始状态的各种信息压入队列中。
2.判断队列是否为空，若为空，退出循环，打印移动步骤，结束。
3.取出队头元素判断是否与目标状态一致。若一致,则退出循环，输出移动步骤，程序结束。若不一致,则分别判断空格向左、向上、向下以及向右能否移动。                                                                 5.若可以移动，求其康托值，然后压进队列。并跳转到步骤四。

2.算法实现

①队列

因为此队列要存的东西是一个结构体，因此也要把其类型定为结构体ma

②康托展开

在此代码中，康托展开用于判重。要将一个3*3的矩阵换为一个数。首先，我们要把此二维数组变为一维的。

    int d[10],len = 0;
    for (int i = 1; i <= 3; i++)
    {
        for (int j = 1; j <= 3; j++) 
        {
            d[++len] = ak.a[i][j];
        }
    }

然后，进行康拓转化。最后就是这样

int kt(ma ak)
{
    int d[10],len = 0;
    for (int i = 1; i <= 3; i++)
    {
        for (int j = 1; j <= 3; j++) 
        {
            d[++len] = ak.a[i][j];
        }
    }
    int s=1;
    for(int i=1;i<=9;i++)
    {
        int index=1,f=1,count=0;
        for(int j=i+1;j<=9;j++)
        {
            f=f*index,index++;
            if(d[i]>d[j]) count++;
        }
        s=s+count*f;
    }
    return s;
}

 ③标记

很简单，用数组flag标记康托值即可

---

四.AC代码

#include<bits/stdc++.h>
using namespace std;
struct ma{
    int a[10][10],x0,y0,ans,kt; 
};
int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};
queue<ma>q;
bool flag[400000];
int kt(ma ak)
{
    int d[10],len = 0;
    for (int i = 1; i <= 3; i++)
    {
        for (int j = 1; j <= 3; j++) 
        {
            d[++len] = ak.a[i][j];
        }
    }
    int s=1;
    for(int i=1;i<=9;i++)
    {
        int index=1,f=1,count=0;
        for(int j=i+1;j<=9;j++)
        {
            f=f*index,index++;
            if(d[i]>d[j]) count++;
        }
        s=s+count*f;
    }
    return s;
}
int main()
{
    ma shi,mo;
    for(int i=1;i<=3;i++)
    {
        for(int j=1;j<=3;j++)
        {
            scanf("%d",&shi.a[i][j]);
            if(shi.a[i][j]==0)
            {
                shi.x0=i,shi.y0=j;
            }
        }
    }
    shi.ans = 0;
    shi.kt = kt(shi);
    flag[shi.kt] = 1;
    q.push(shi);
    for(int i=1;i<=3;i++)
    {
        for(int j=1;j<=3;j++)
        {
            scanf("%d",&mo.a[i][j]);
        }
    }
    mo.kt=kt(mo);
    while(!q.empty())//q非空，可以走
    {
        for(int i=0;i<4;i++)//四个方向
        {
            ma ac=q.front();
            int nx = ac.x0 + dx[i];
            int ny = ac.y0+ dy[i];
            if(nx>=1&&ny>=1&&nx<=3&&ny<=3)
            {
                swap(ac.a[ac.x0][ac.y0],ac.a[nx][ny]);
                ac.x0=nx;
                ac.y0=ny;
                //将0与目标数交换
                ac.ans++;//步数加1
                ac.kt=kt(ac);
                //康托判重
                 if (!flag[ac.kt])
                {
                    flag[ac.kt] = 1;
                    q.push(ac);
                    //加入队列
                    if(ac.kt==mo.kt)
                    { 
                        printf("%d",q.back().ans);
                        exit(0);
                    }
                }
            }
        }
        q.pop();
        //弹出已遍历完所有情况的矩阵
    }
}