常见文本相似度计算方法简介_文本相似度匹配实现

作者名: 李鹏宇

0引言

在自然语言处理任务中，我们经常需要判断两篇文档是否相似、计算两篇文档的相似程度。比如，基于聚类算法发现微博热点话题时，我们需要度量各篇文本的内容相似度，然后让内容足够相似的微博聚成一个簇；在问答系统中，我们会准备一些经典问题和对应的答案，当用户的问题和经典问题很相似时，系统直接返回准备好的答案；在监控新闻稿件在互联网中的传播情况时，我们可以把所有和原创稿件相似的文章，都看作转发，进而刻画原创稿件的传播范围；在对语料进行预处理时，我们需要基于文本的相似度，把重复的文本给挑出来并删掉……总之，文本相似度是一种非常有用的工具，可以帮助我们解决很多问题。

这里对计算文本相似度涉及的模型和算法，进行简要的整理。目录如图0-1。

图0-1 目录

1文本相似度计算任务的简单分析

文本的相似性计算，是我们常说的“文本匹配任务”的一种特殊情况。

1.1任务目标

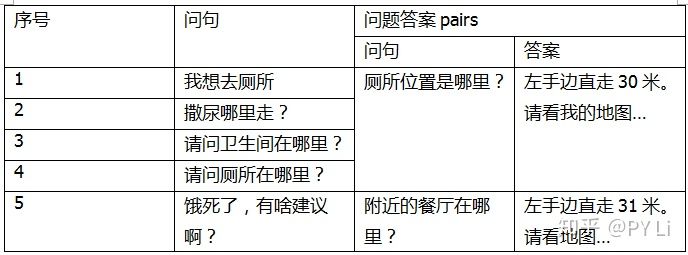
一般来说，文本相似度计算任务的输入，是两篇文档，比如表1-1的前两个句子；输出是两篇文档的相似程度，通常用[0,1]区间内的小数来表示。作为一个懂人话的人类，我知道句子1和句子2的内容是一样的，并认为计算二者的相似性非常简单。

假如说，我们要判断1万对文档的相似性，或者在1秒内判断100对文档的相似度呢？那我就不行了，需要上机器。

大家在生活里和可能已经用到了文本相似度计算支持的东西。很多产品(APP,网站，导游机器人等等)配备了问答系统，允许用户用自然语言向系统发出各种请求。系统会理解用户的语言，然后返回一定形式的内容并展示在终端展里，作为对用户的回答。有些问题比较经典，大家经常问到。工程师或者领域专家会把这些问题和对应的答案收集并存储起来——当用户再次问到类似的问题时，直接返回现成的答案即可。“类似”与否的判断，需要使用文本相似度计算来支持。

那么，如何让机器替我们完成文本相似度的计算呢？

表1-1 我对机器人说的话

1.2候选方案

文本相似度计算方法有2个关键组件,即文本表示模型和相似度度量方法，如表1-2。前者负责将文本表示为计算机可以计算的数值向量，也就是提供特征；后者负责基于前面得到的数值向量计算文本之间的相似度。

从文本表示模型和相似度度量方法中选择合适的，就可以组合出一个文本相似度计算方案。

表1-2 常见的文本表示模型和相似度度量方法

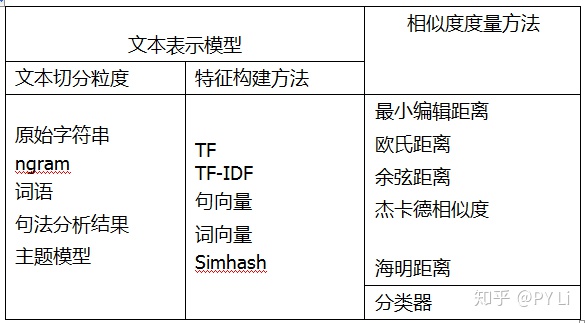
使用这个菜单里的选项，我们可以组合出非常多的文本相似度计算方案。那么，每一种方案都可以用来解决什么样的任务呢？要回答这个问题，需要了解一下每一个组件的原理和特点。后面会从有无监督、文本切分粒度、特征构建、距离计算方法4个维度介绍文本相似度计算方法。

我们有时候强调文档之间的差异性，会提“文本距离”；有时候强调文本之间相似的程度，会提“文本相似度”。“距离”和“相似度”是对立统一的两个东西，可以用一定的算法相互转化。这里的介绍会在两个概念之间来回跳跃，要注意区分。

2有监督和无监督的文本相似性计算

文本相似度计算方法分为有监督和无监督两类。

有监督方法，就是用朴素贝叶斯分类器之类的有监督模型来判断文本相似性或者计算相似度。这类方法要求有一定数量的标注语料，构建的代价比较高；由于训练语料通常无法做得很大，模型的泛化性不够，实际用起来会有点麻烦；距离计算环节的复杂度会比较高。

无监督方法，就是用欧氏距离等方法，直接计算文本之间的距离或者相似度。这类方法的特点是：不需要标注语料，特征工程或者参数估计可以使用很大的数据；很多方法对语言的依赖比较小，可以应对多语种混杂的场景；距离计算环节复杂度较低。

通常来说我们首先考虑无监督模式。

3文本切分粒度

3.1n-gram

我们常说的“n-gram语言模型“，指的是一类使用相同文本切分方式的语言模型。这种切分方式非常简单：使用一个长度为n的窗口，从左到右、逐字符滑过文本；每一步，会框到一个字符串，就是一个gram；文本里所有的gram就是该文本的切分结果。如表3-1所示，是几种常见的n-gram切分结果。

表3-1 “我爱北京天安门”的n-gram表示

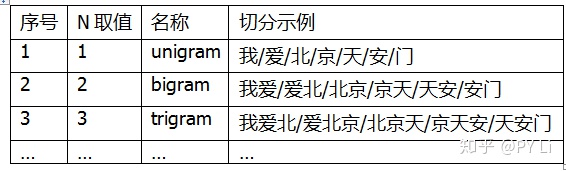
n-gram越长，词表越大。一份中文语料的Trigram词表可以达到上百万的规模。要是来个quadgram，由于内存消耗较大、特征很稀疏，我们的工作会很难开展。一般来说，bigram的效果就挺好了。

3.2分词

另外一种文本切分方式就是分词，比如将“我爱北京天安门”切分为“我/爱/北京/天安门”。分词的目的是将文本切分为有句法意义的一个个小单元，便于人和机器理解文本的内容。

在NLP进入深度学习时代之前，分词是中文信息处理的基础任务。语言这种序列数据，具有很强的时间/空间相关性。在一段文本序列的某些位置，会出现相关性特别高的若干连续字符，比如“我爱北京天安门”里的“天安门”，这3个字符内部之间的相关性明显高于它们同其他字符的相关性。

相比n-gram，分词的优势是，在字符相关性较小的位置进行切分、造成的信息损失比较小。由于分词降低了文本的相关性，可以提升一些带有独立性假设的模型。

当然，ngram由于极高的计算速度，仍然占有一定的市场。

3.3句法分析

我们可以基于句法分析的结果，从文本中抽取短语，作为文本的表示。这样得到的特征非常稀疏，适合精度要求较高的场景。

3.3.1粗暴版句法分析

我们可以用一些规则或者模型，从文本中提取特定的词语组合，作为文本的切分结果。比如用“第一个名词+第一个动词+第二个名词”这个规则处理“我爱北京天安门”的结果是“我+爱+北京”。

3.3.2正经句法分析

可以使用正经的句法分析工具，提取“主+谓+宾”之类的，作为文本的切分结果。句法分析的耗时比较高，适合数据量小的场景。

3.4主题模型

可以使用主题模型来提取文本的主题，用主题词来表示文本。常见的主题模型有PLSA、LDA以及它们的变种(LSA适用于教学场景；还有很多优秀的主题模型，所知甚少，不多介绍)。主题模型在训练的过程中，学习到了语料的全局信息，因此具有一定的“联想”或者说“推理”能力，可以基于文档内容推测出文档字面没有明说的一些信息。因此，主题模型可以处理一些需要关注隐藏信息的场景。

当然了，主题模型的训练比较慢、对语料规模和质量有较高的要求，因此考虑是否使用的时候需要慎重。

4特征构建方法

文本相似度计算任务的第二步，是用数值向量表示文本的内容。通常，我们会用一个数值向量描述文本在语义空间中的位置。

4.1TF与TF-IDF

4.1term frqeuncy向量

词袋模型(bag of words)假设，文本里的term（虽然名字里是”words”，实际上我们也可以用n-gram之类的切分方式）之间相互独立，也就是词语A的出现和词语B的出现没有关系。

我们可以用独热编码表示所有的term，然后对文本中的term去重，最后把得到的term的编码加起来,就得到了TF向量。

TF向量对常用词比较友好。假设有一份红学文集构成的语料，里面“红楼梦”“贾宝玉”这样的词语几乎会出现在每一篇文档里，相应的频率还很高。结果就是这样的词语“统治”了TF向量，导致两篇文档比较相似。换句话说，TF对文档的区分能力比较低。

4.2词向量和句向量

4.3simhash

4.3.1simhash简介

Simhash是敏感哈希算法在文本特征提取任务中的应用。它会把一篇文档映射为一个长度为64、元素值为0或1的一维向量。这样我们就可以使用某种距离计算方式，计算两篇文本的距离和相似度了。一般来说，与simhash配合的是海明距离。

4．3.2simhash的适用场景

Simhash的特点是，对文本的“相同”与否特别敏感：当两篇文档相同时，相似度为1；当其中一篇略有不同，相似度会有明显降低。因此非常适合用来判断两篇文档内容是否相同。

另外simhash的计算比较简单，速度上有一定优势。如果配合一定的检索策略来召回候选相似文档，simhash可以用来对海量文档进行去重——这就是simhash最常见的一个应用场景。

5距离的度量方式

假设表1-1的3句和4句分词结果分别为:

5.1欧氏距离

5.1.1欧氏距离的计算方法

假设我们有两个数值向量,表示两个实例在欧式空间中的位置:

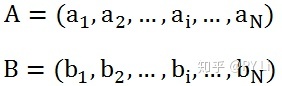
#########纠错开始#########

二者的欧氏距离不是这样计算的:

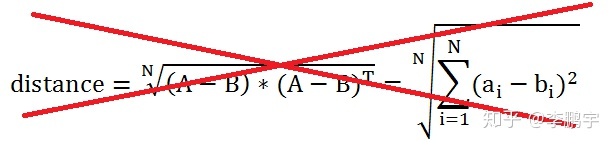
当初写文章时，我把把Lp范数和L2范数混淆了，写了一个错误的公式。L2范数，即欧氏距离，应该这样计算:

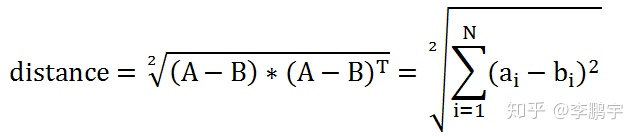
范数的详情可以参考

CSDN-专业IT技术社区-登录​blog.csdn.net/shijing_0214/article/details/51757564

这里感谢

知乎用户​www.zhihu.com/people/zhou-zong-59-7/activities

的提醒，指出了我的错误。这里对后面的类似错误也进行了修改。

##########纠错结束############

如图5-1，二维空间(平面)里有两个点

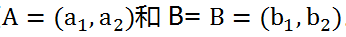
二者在X轴上的差异大小是

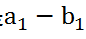
,在Y轴上的差异是

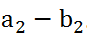
综合两个坐标轴上的差异，就得到了两点之间的距离:

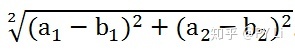
欧式距离是最符合我们直觉的一种距离度量方式。它认为事物的所有特征都是平等的。两个实例在所有维度上的差异的总和，就是二者的距离。

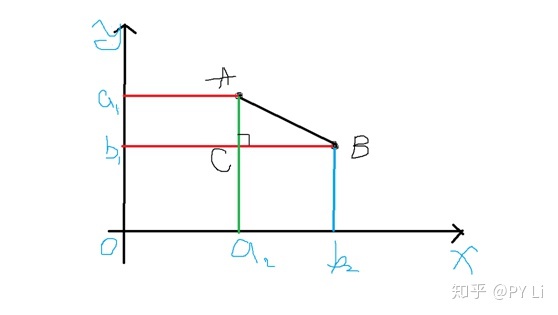
图5-1 二维空间中的两个点的距离

5.1.2基于欧式距离的文本相似度计算

假设我们的词汇表是(部分词语在特征选择中删掉了):

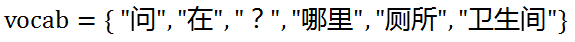
那么两个句子对应的TF向量分别是:

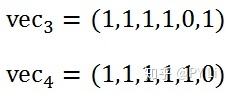
二者的欧氏距离为:

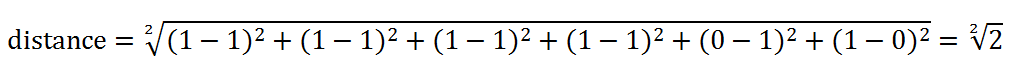
这样，我们就可以计算相似度了，常用的方式是:

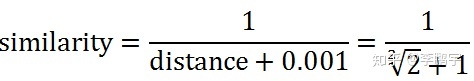
分母中的”1”用来保证相似度最高是1。当然，相似度可以根据场景要求花式定义。

5.2余弦距离

5.2.1余弦距离的计算方式

余弦距离来源于向量之间夹角的余弦值。假设空间中有两个向量:

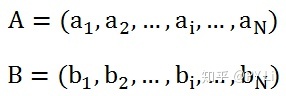
那么二者的夹角的余弦值等于:

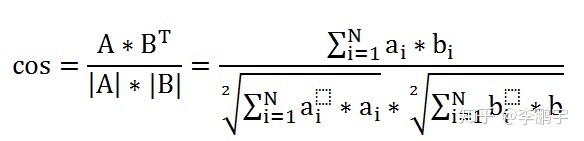
这个计算方式是可以推导出来的——由于形式简单，我们可以把它当做勾股定理这样的知名定理来对待。如图5-2，是二维平面上，两个向量之间夹角的示意图，我们可以基于勾股定理凑出上面的式子。

图5-2 二维空间中两个向量的夹角

5.2.2基于余弦距离的文本相似度

向量的夹角余弦值可以体现两个向量在方向上的差异，因此我们可以用它来度量某些事物的差异或者说距离。

在文本相似度计算任务中，为了让数据适合余弦夹角的概念，人们假想：语义空间中存在一个“原点”；以原点为起点、文本特征数组(这里为了避免与“语义向量”混淆，借用了“数组”这个名称)表示的点为终点 ，构成了一个向量，这就是代表了文本语义的“语义向量”。语义向量的方向，描述了文本的语义。因此，我们可以用两篇文档的语义向量的夹角余弦值来表示它们的差异。这个余弦值通常被称为“余弦距离”。

提取文本特征后，可以将数值向量套入前面的余弦值计算公式，既可以得到两篇文本的余弦距离:

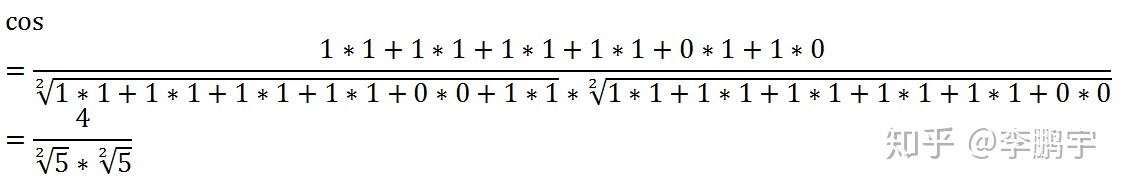
余弦值的取值范围是[-1,1]（感谢无知的小猪 - 知乎的提醒。此处取值范围原来写的是[0,1]，可能是当时我误以为分子取值大于0.实际上分子是可以小于0的），我们可以用一个简单的方式得到余弦相似度:

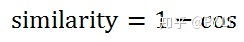
当文本特征维度比较高的时候，在余弦距离的视角下，文本之间的区分度越来越小。

这导致我们在设定“是否相同”的阈值时，遇到困难。因此余弦距离比较适用于文本较短，也就是特征维度较低的场景。

5.3Jacard相似度

5.3.1杰卡德相似度的计算方式

杰卡德相似度一般被用来度量两个集合之间的差异大小。假设我们有两个集合A和B，那么二者的杰卡德相似度为：

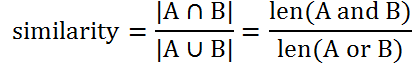
杰卡德距离的思想非常简单:两个集合共有的元素越多，二者越相似；为了控制距离的取值范围，我们可以增加一个分母，也就是两个集合拥有的所有元素。

5.3.2基于杰卡德相似度的文本相似度计算

我们可以把文档看做是词语的集合,然后用杰卡德距离相似度度量文档之间的差异。

表1-1的3句和4句的杰卡德相似度就是:

我们可以基于这个距离计算得到杰卡德距离:

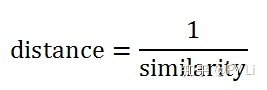
5.3.3杰卡德相似度的改装

我的同事兰博同学认为，杰卡德相似度忽略了文本长度差异。“我让你三掌！”和“我让你三掌！我让你三掌！我让你三掌!”这两句话，使用杰卡德相似度得到的相似度是1，即完全相同。事实上，二者的含义还是略有区别的(一般来说，重要的事情才需要说三遍)。如何区分这两句话呢？

他的解决思路是，在杰卡德相似度的分母增加一个对文本长度差异的惩罚:

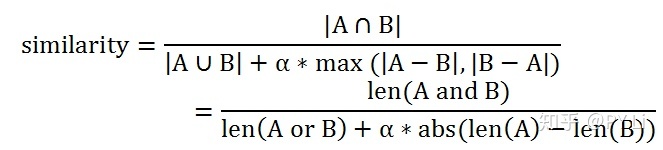
式中

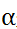
是一个超参数，可以根据相似度的效果调整大小。

5.4海明距离

海明距离是simhash算法的御用距离算法。

5.4.1海明距离的计算方式

海明距离的计算方式非常简单。如5.1.1所述，两个句子可以用词袋模型来表示:

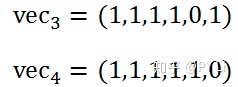
我们比较两篇文档的特征向量的每一个维度，判断各个维度上取值是否相等。不相等的维度越多，两篇文档差异越大。海明距离的计算方式如下:

其中，

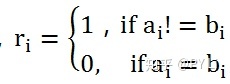
5.4.2基于海明距离的文本相似度

换个角度，两篇文档的特征向量里，相等的维度越多，相似度就越大。相似度的计算方法如下:

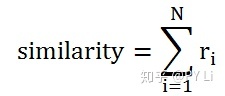
其中，

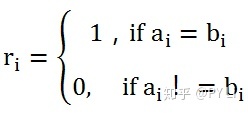
5.5最小编辑距离

最小编辑距离是一种经典的距离计算方法，用来度量字符串之间的差异。它认为，将字符串A不断修改(增删改)、直至成为字符串B，所需要的修改次数代表了字符串A和B的差异大小。当然了，将A修改为B的方案非常多，选哪一种呢？我们可以用动态规划找到修改次数最小的方案，然后用对应的次数来表示A和B的距离。计算方法见:

PY Li：最小编辑距离与动态规划25 赞同 · 2 评论文章

从定义上可以看出，最小编辑距离比较适合判断字面上的相似性，对文本字语义上的相似性无能为力。

6结语

相似度计算不光在文本数据处理里经常用到，在图像、音频、生物信息等等类型数据的处理中也有很高的出场率。对应地，相似度计算可以帮助我们解决生产活动里的很多具体问题。因此，它是一种非常有用的方法，值得我们仔细琢磨。

注意：本文为李鹏宇(知乎个人主页李鹏宇 - 知乎)原创作品，受到著作权相关法规的保护。如需引用、转载，请注明来源信息：（1）作者名，即“李鹏宇”；（2）原始网页链接，即当前页面地址。如有疑问，可发邮件至我的邮箱:lipengyuer@126.com。