Stochastic Approximation 随机近似方法的详解之（二）Robbins-Monro Algorithm_rm算法

6.2 Robbins-Monro Algorithm

RM算法是随机近似领域的先驱性工作。众所周知的随机梯度下降算法是RM算法的一种特殊情况。后面我们再介绍具体的细节。

先看一个例子：

我们想要去求下面这个等式的根，

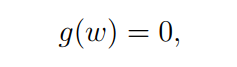
BTW，很多问题可以被转化为求根问题。比如，$J(w)$ 是我们要最小化的目标函数。它其实可以被等价转化为下面这个等式的求根问题：

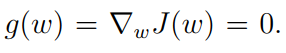
当函数g的表达式已知或者它的导数已知的时候，求解当然很简单。但是当g未知的时候（比如是一个神经网络或者g不能被精确观察到的时候），问题就困难起来了。这个时候我们知道的是什么呢？

只有输入$w$ 和带有噪声的输出$\tilde{g}(w,\eta )$，我们要根据他们两个来解这个$g(w)=0$的方程。

RM 算法如下：

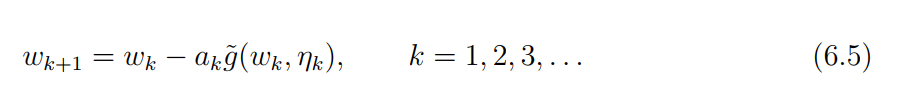
其中$w_k$是第k次对根的估测，$\tilde{g}(w,\eta )$ 是第 $k$ 个有噪声的观测。$a_k$是一个正的系数。

下面我们来看一个应用RM算法的例子：

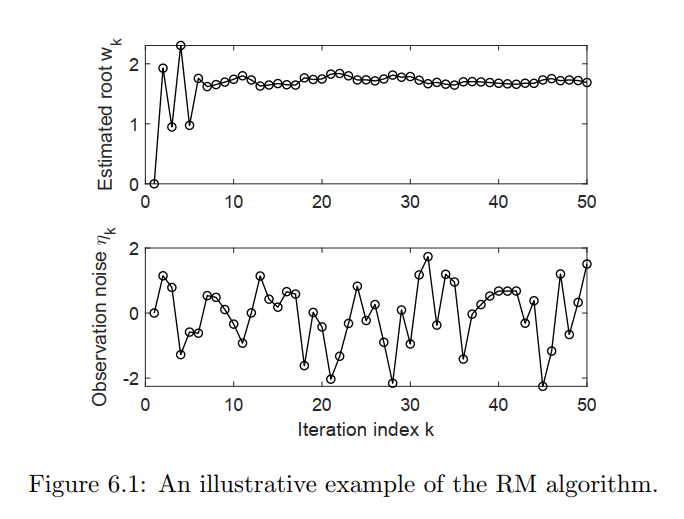
我们再看另一个例子：
$g(w)=\tanh (w-1)$ ，我们知道$g(w)=0$的根为1，我们从$w_1=3$开始迭代，并且设定$a_k=1/k$，结果是什么呢？下图展示了$w_i$的动态更新过程。

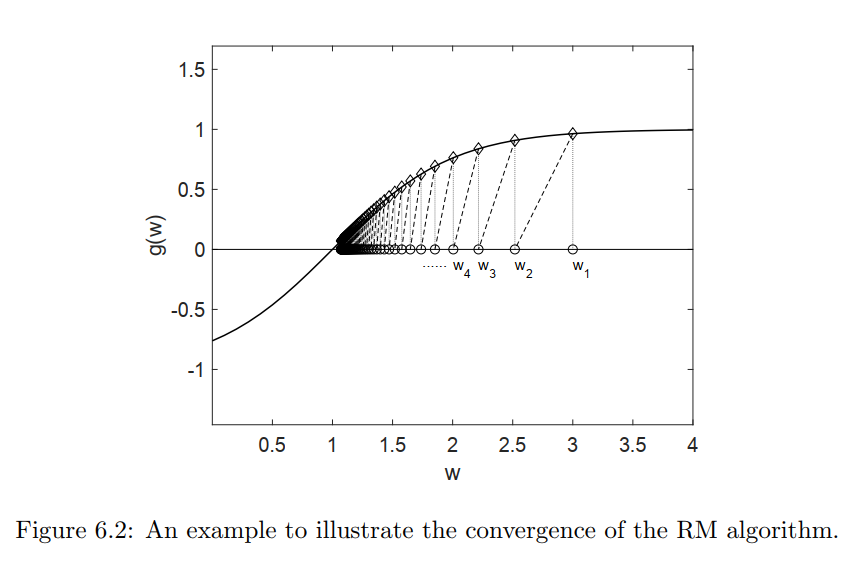
RM算法的收敛特性怎么去证明呢？
见《Mathematical Foundation of Reinforcement Learning》Shiyu Zhao P107

应用RM到均值估测上面

均值估计的原始问题为：

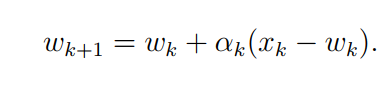
我们提到，在${\alpha }_k$满足一些温和的条件的时候，w是会收敛到$\mathbb{E}[X]$ 的。
我们接下来说明它是特殊的RM算法。

建立如下函数，求解w的问题就变成了求$g(w)=0$的问题。

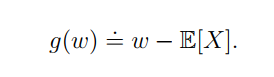
下面是我们观测到的输出：

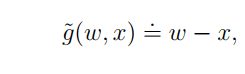
如何去解释这个输出呢？其实它可以拆分为$\tilde{g}(w)+\eta$ 这就符合了RM算法的设定。可以使用RM方法求解了。

其实我们发现了，在$\tilde{g}(w_k,{\eta }_k)$展开之后，和前面用迭代更新方法求均值是一模一样的。

对RM算法的收敛性感兴趣的朋友可以参考我的下一篇搬运：
Dvoretzky’s convergence theorem