- 1(read/write、select、getsockopt、signal)实时判断socket连接状态/是否断开_getsockopt函数判断sock链接状态
- 2搭建linux服务器详细教程_linux文件服务器搭建
- 3Java 实现一个单例模式_Java实现单例模式的两种方式
- 4Altium Designer学习之1——Stm32f103c8t6最小系统板(PCB制图,手把手教程)
- 5Kubernetes手动指定pod运行位置_k8s查看pod在哪个node上
- 6python(django框架)化妆品淘宝电商销售数据可视化和商品推荐系统设计与实现_基于python淘宝数据可视化
- 7推荐几款便宜幻兽帕鲁(Palworld)联机服务专用服务器_幻兽帕鲁 华为云服务器
- 8QueryWrapper中or和and并列使用_querywrapper and or
- 9【机器学习->预处理】pandas数据预处理:读取csv、处理缺失数据、转换为tensor_pandas 读第一行缺失的csv
- 10IEEE 802.1Q封装的VLAN数据帧格式_vlan帧格式
【清风数模】时间序列分析(spss实现,详细笔记)_spss时间序列分析实例
赞
踩
时间序列分析
前言
时间序列也称动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列。时间序列分析天致可分成三大部分,分别是描述过去、分析规律和预测未来,本讲将主要介绍时间序列分析中常用的三种模型:季节分解、指数平滑方法和ARIMA模型,并将结合Spss软件对时间序列数据进行建模。
时间序列数据
下面两张陶虹的照片也算是时间序列数据了。


例如:
(1)从出生到现在,你的体重的数据(每年生日称一次)。
(2)中国历年来GDP的数据。
(3)在某地方每隔一小时测得的温度数据。
时间序列的基本概念
时间序列也称动态序列,是指将某种现象的指标数值按照时间顺序排列而成的数值序列。
时间序列由两个组成要素构成:
1、第一个要素是时间要素;
年、季度、月、周、日、小时、分钟、秒
2、第二个要素是数值要素。
时间序列根据时间和数值性质的不同,可以分为时期时间序列和时点时间序列。
时期序列中,数值要素反映现象在一定时期内发展的结果;
时点序列中,数值要素反映现象在一定时点上的瞬间水平。
区分时期和时点序列
时期序列可加,时点序列不可加
例如:
(1)从出生到现在,你的体重的数据(每年生日称一次)。
(2)中国历年来GDP的数据。
(3)在某地方每隔一小时测得的温度数据。
(1)和 (3) 是时点时间序列;
(2)是时期时间序列
时期序列中的观测值反映现象在一段时期内发展过程的总量,不同时期的观测值可以相加,相加结果表明现象在更长一段时间内的活动总量;而时点序列中的观测值反映现象在某一瞬间上所达到的水平,不同时期的观测值不能相加,相加结果没有实际意义。
时间序列分解
因为时间序列是某个指标数值长期变化的数值表现,所以时间序列数值变化背后必然蕴含着数值变换的规律性,这些规律性就是时间序列分析的切入点。
一般情况下,时间序列的数值变化规律有以下四种:
- 长期变动趋势
- 季节变动规律
- 周期变动规律
- 不规则变动(随机扰动项)
一个时间序列往往是以上四类变化形式的叠加。
长期趋势:T
长期趋势(Secular trend,T)指的是统计指标在相当长的一段时间内,受到长期趋势影响因素的影响,表现出持续上升或持续下降的趋势,通常用字母T表示。例如,随着国家经济的发展,人均收入将逐渐提升;随着医学水平的提高,新生儿死亡率在不断下降。
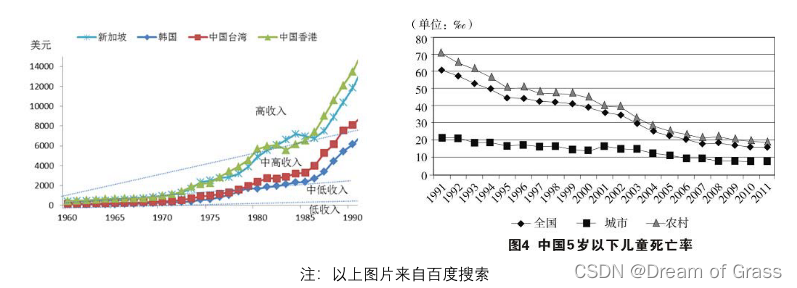
季节趋势:S
季节趋势(Seasonal Variation,S)是指由于季节的转变使得指标数值发生周期性变动。这里的季节是广义的,一般以月、季、周为时间单位,不能以年作单位。例如雪糕和棉衣的销量都会随着季节气温的变化而周期变化;每年的长假(五一、十一、春节)都会引起出行人数的大量增加。
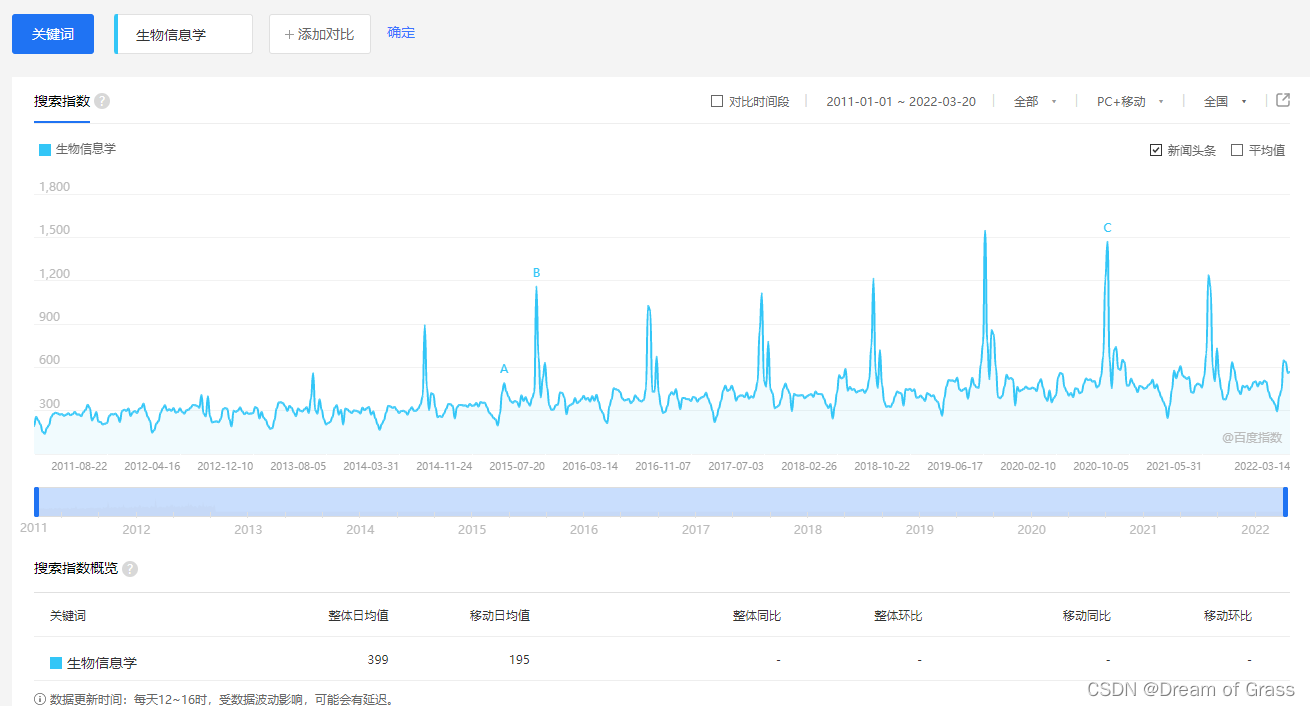
循环变动:C
循环变动(Cyclical Variation,C)与季节变动的周期不同,循环变动通常以若干年为周期,在曲线图上表现为波浪式的周期变动。这种周期变动的特征表现为增加和减少交替出现,但是并不具严格规则的周期性连续变动。最典型的周期案例就是市场经济的商业周期和的整个国家的经济周期。
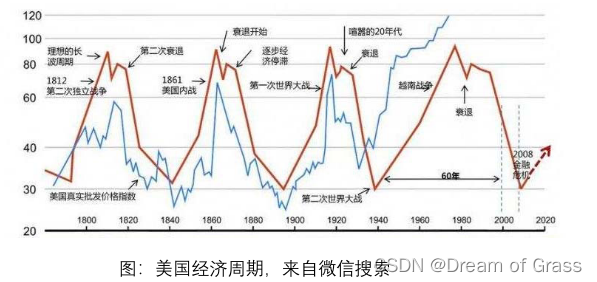
不规则变动:I
不规则变动(Irregular Variation,I)是由某些随机因素导致的数值变化,这些因素的作用是不可预知和没有规律性的,可以视为由于众多偶然因素对时间序列造成的影响(在回归中又被称为扰动项)。
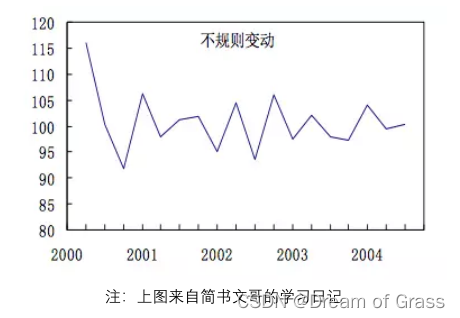
以上四种变动就是时间序列数值变化的分解结果。有时这些变动会同时出现在一个时间序列里面,有时也可能只出现一种或几种,这是由引起各种变动的影响因素决定的。正是由于变动组合的不确定性,时间序列的数值变化才那么千变万化。
四种变动与指标数值最终变动的关系可能是叠加关系,也可能是乘积关系。
叠加模型和乘积模型
(1)如果四种变动之间是相互独立的关系,那么叠加模型可以表示为:
Y
=
T
+
S
+
C
+
I
Y =T+S+C+I
Y=T+S+C+I
(⑵)如果四种变动之间存在相互影响关系,那么应该使用乘积模型:
Y
=
T
×
S
×
C
×
I
Y =T{\times}S{\times}C{\times}I
Y=T×S×C×I
Y:指标数值的最终变动;
T:长期趋势变动;
S:季节变动;
C:循环变动;
Ⅰ:不规则变动。
使用条件
(1)数据具有年内的周期性时才能使用时间序列分解,例如数据是月份数据(周期为12)、季度数据(周期为4),如果是年份数据则不行。
(2)在具体的时间序列图上,如果随着时间的推移,序列的季节波动变得越来越大,则反映各种变动之间的关系发生变化,建议使用乘积模型;反之,如果时间序列图的波动保持恒定,则可以直接使用叠加模型;当然,如果不存在季节波动,则两种分解均可以。
小例子
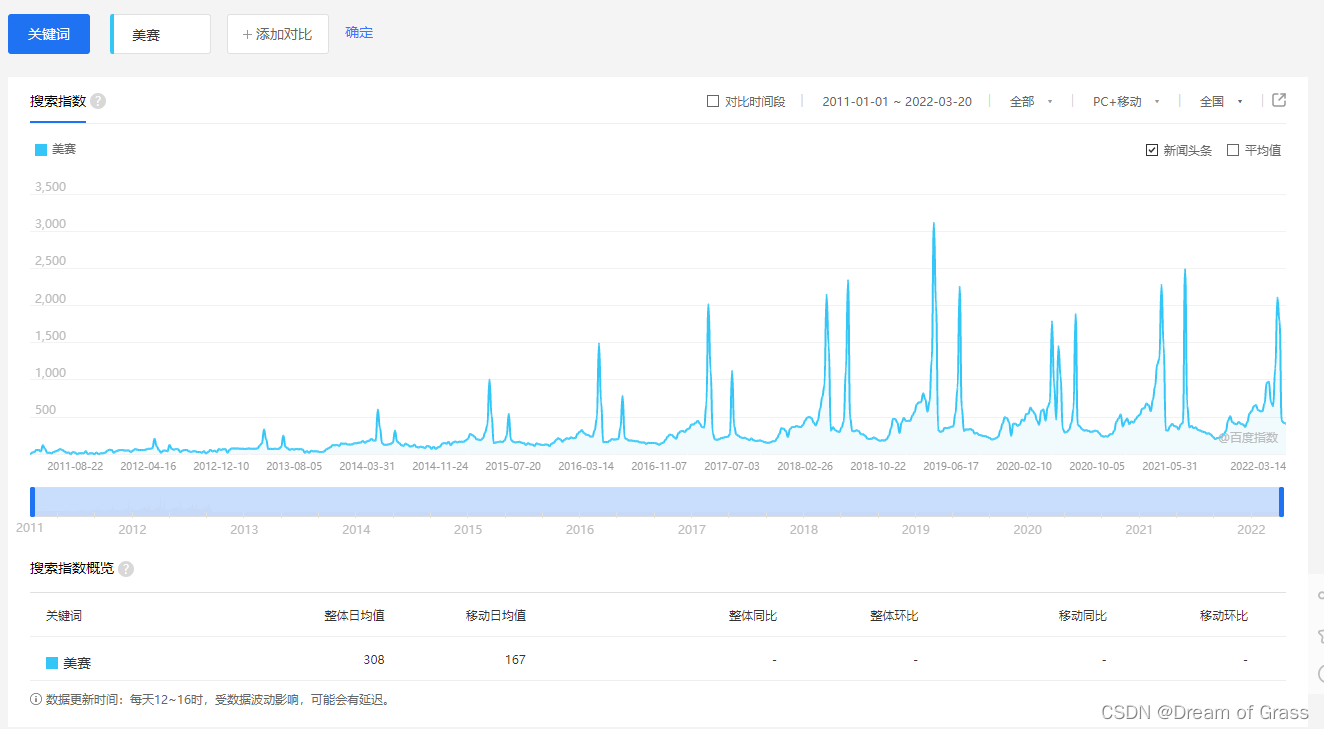
随着时间变化,搜索美赛数据的季节波动越来越大,那么使用乘积模型会更精确。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QssyZeGo-1651230142168)(D:/typora%E5%9B%BE%E7%89%87/image-20220328105008844.png)]](https://img-blog.csdnimg.cn/bfb38117f6494f4ab6413247ab393b5c.png)
随着时间变化,销售数据的季节波动越来越大,那么使用乘积模型会更精确。
实战
预测销售数据
更具某产品2014-2018年嫉妒销售数据,预测未来两年的销售数据。
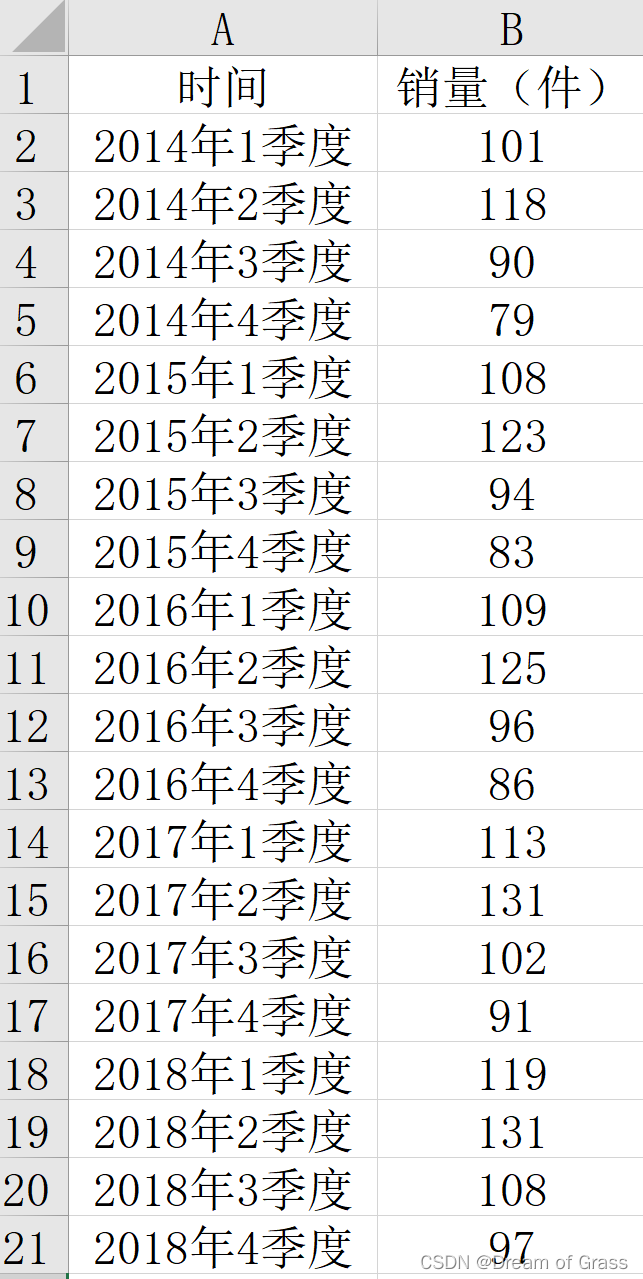
excel小技巧
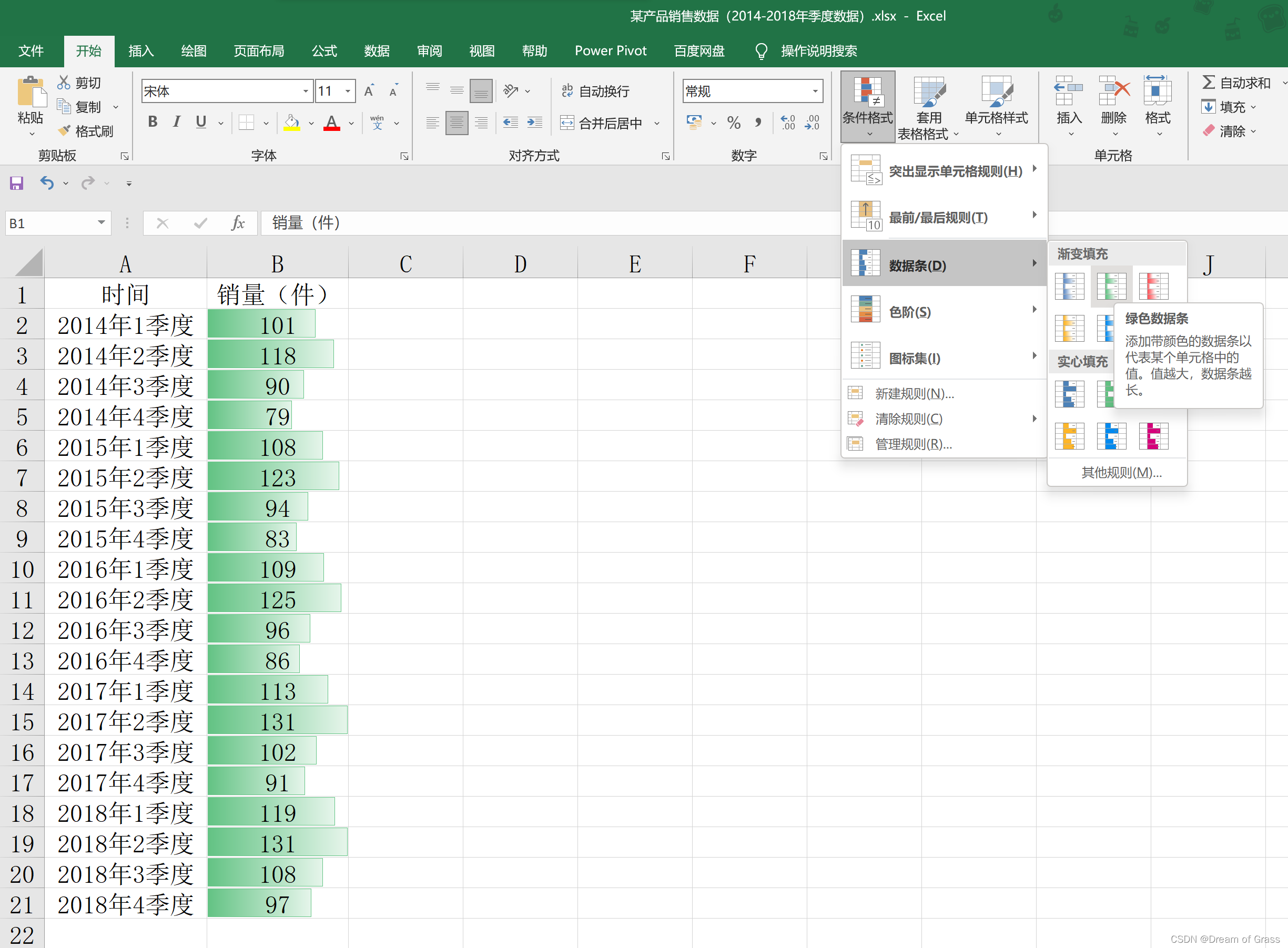
可以在这里用数据条使得数据变得较为直观。
新建时间变量
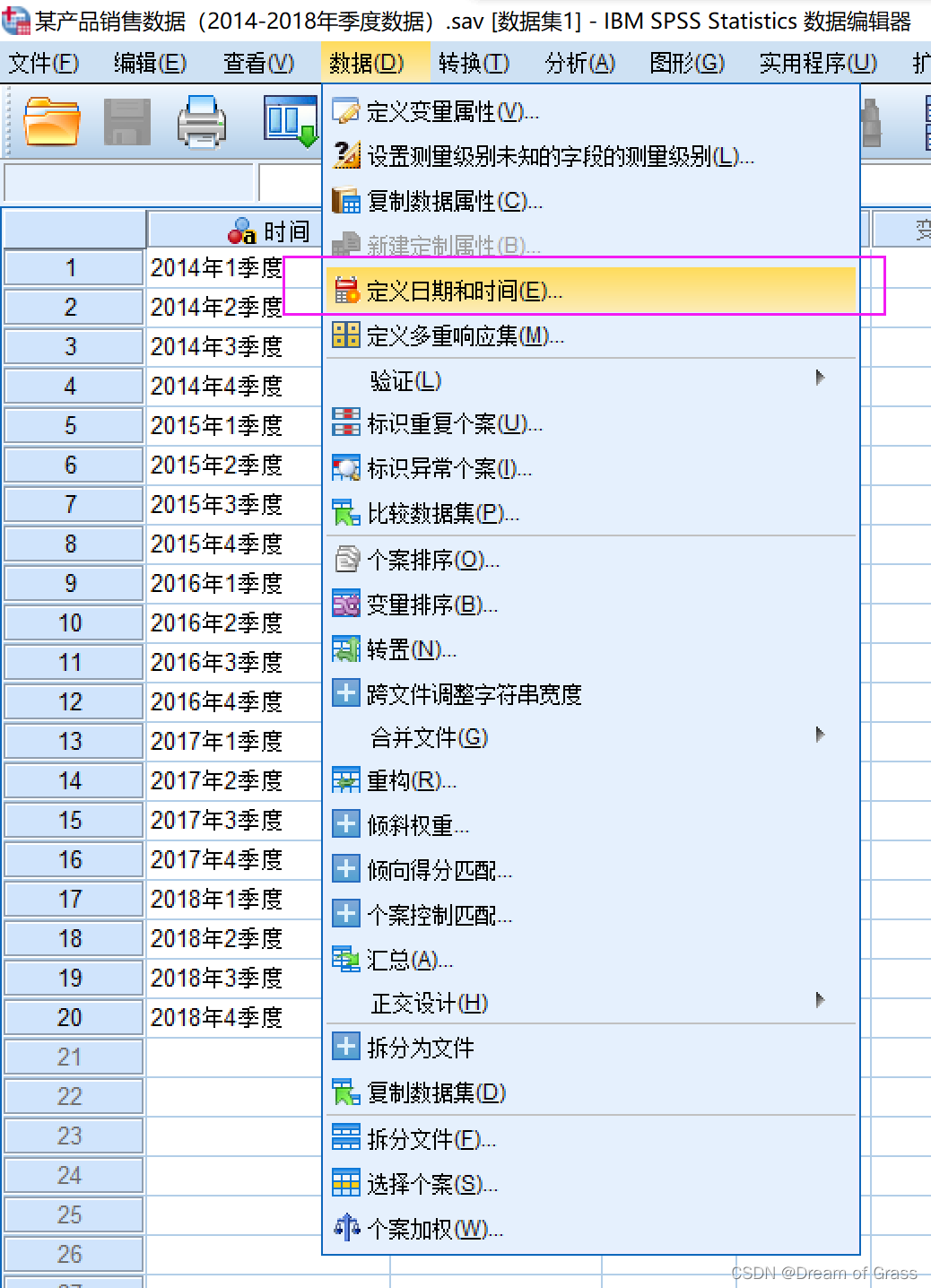
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EJMJGhKX-1651230142171)(D:/typora%E5%9B%BE%E7%89%87/image-20220328143456341.png)]](https://img-blog.csdnimg.cn/f61d2b4a77e4485097c1aef662fd7c09.png)
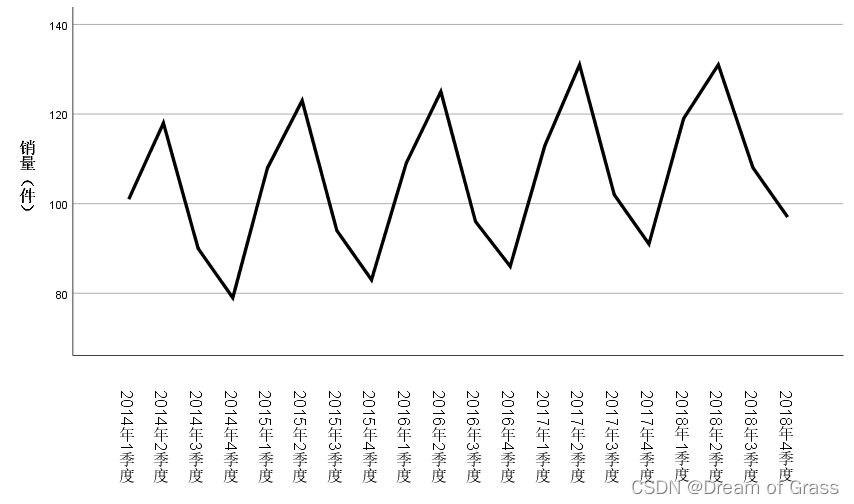
画时间序列图
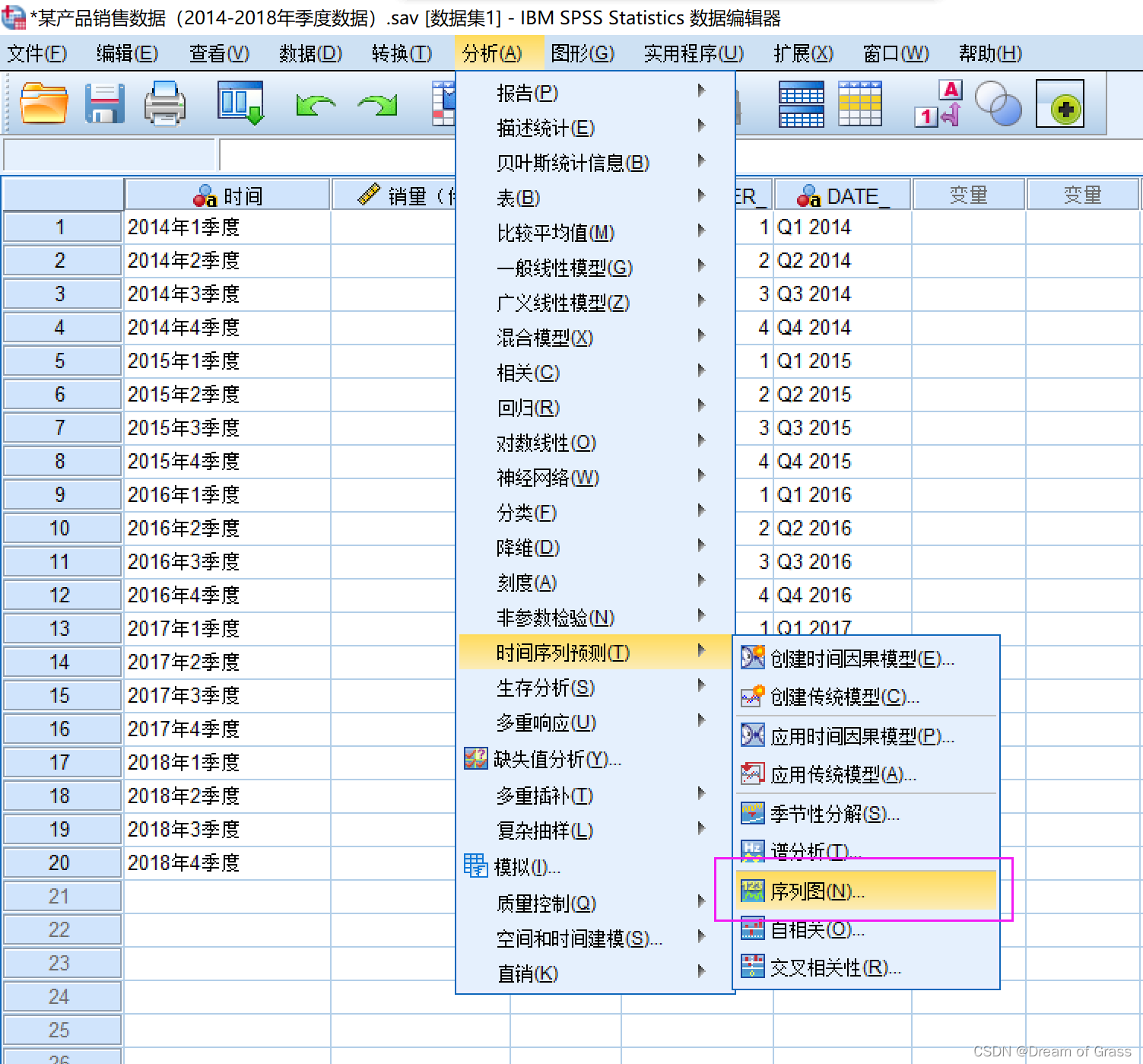
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KiNXU9K1-1651230142173)(D:/typora%E5%9B%BE%E7%89%87/image-20220328143721575.png)]](https://img-blog.csdnimg.cn/cf0f24ccb46a407998a75b6012c61446.png)
Spss时间序列建模器
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oC9bsMou-1651230142174)(D:/typora%E5%9B%BE%E7%89%87/image-20220328144132128.png)]](https://img-blog.csdnimg.cn/6efa2e31202d4c73928e7642ed1ad3cf.png)
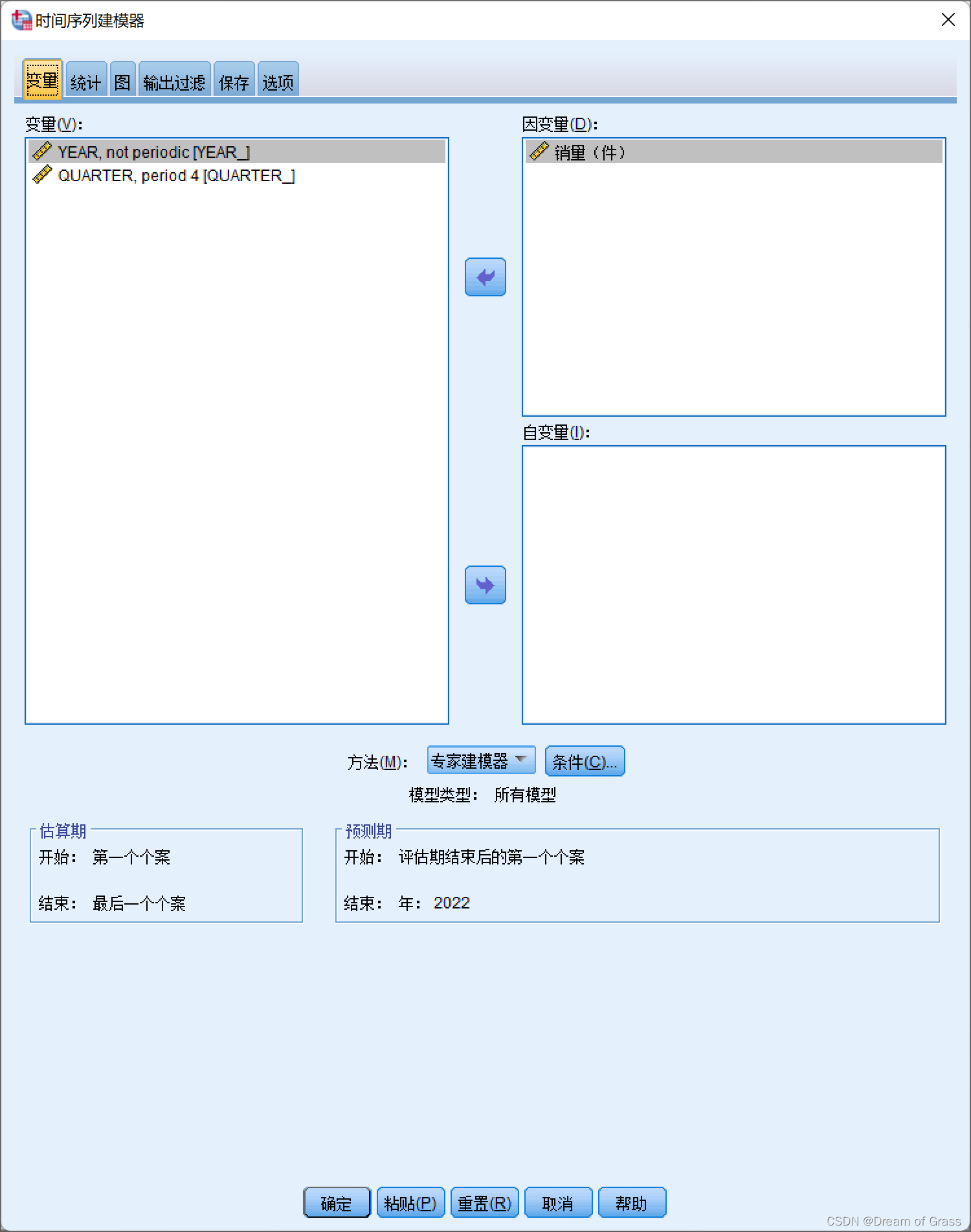

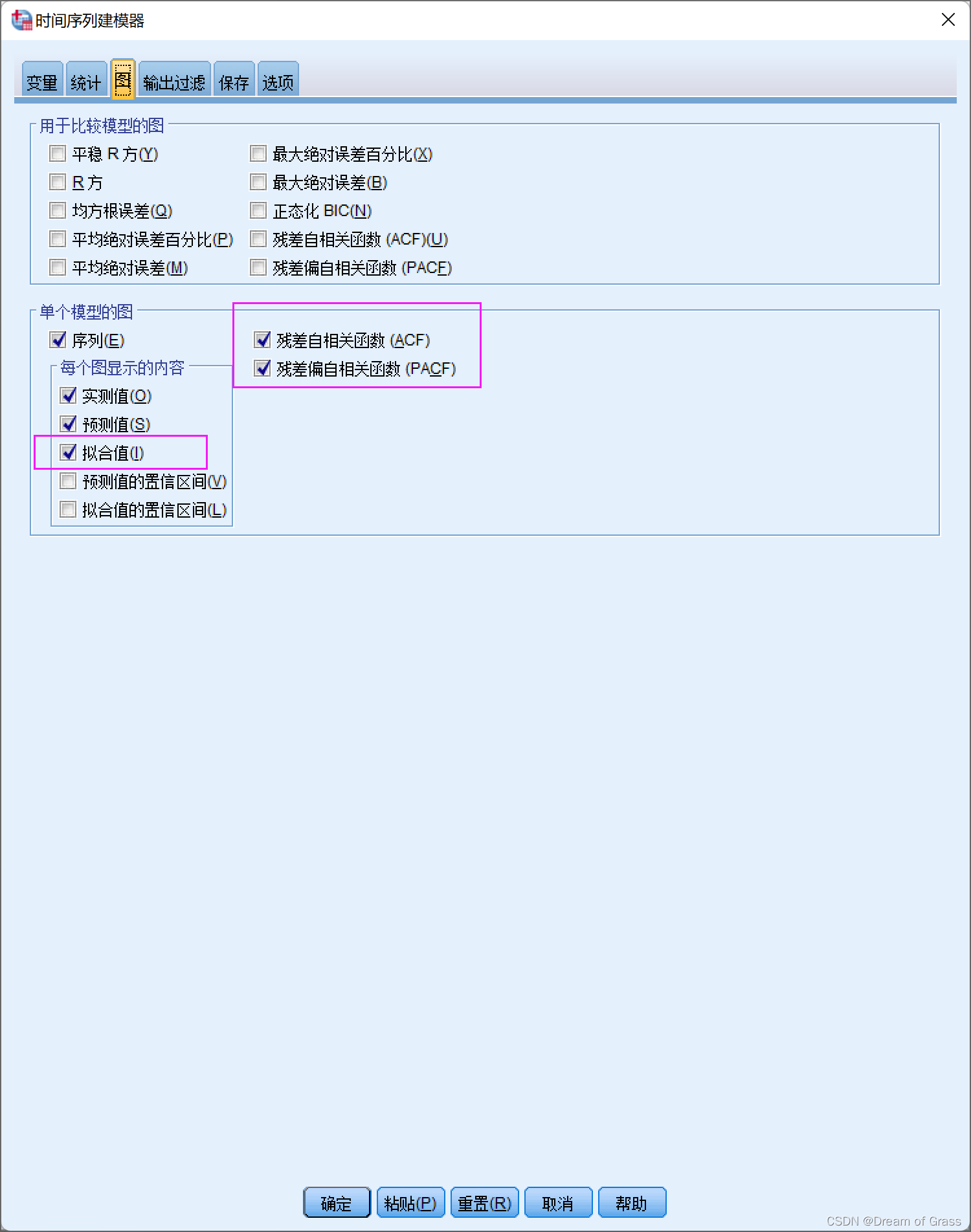
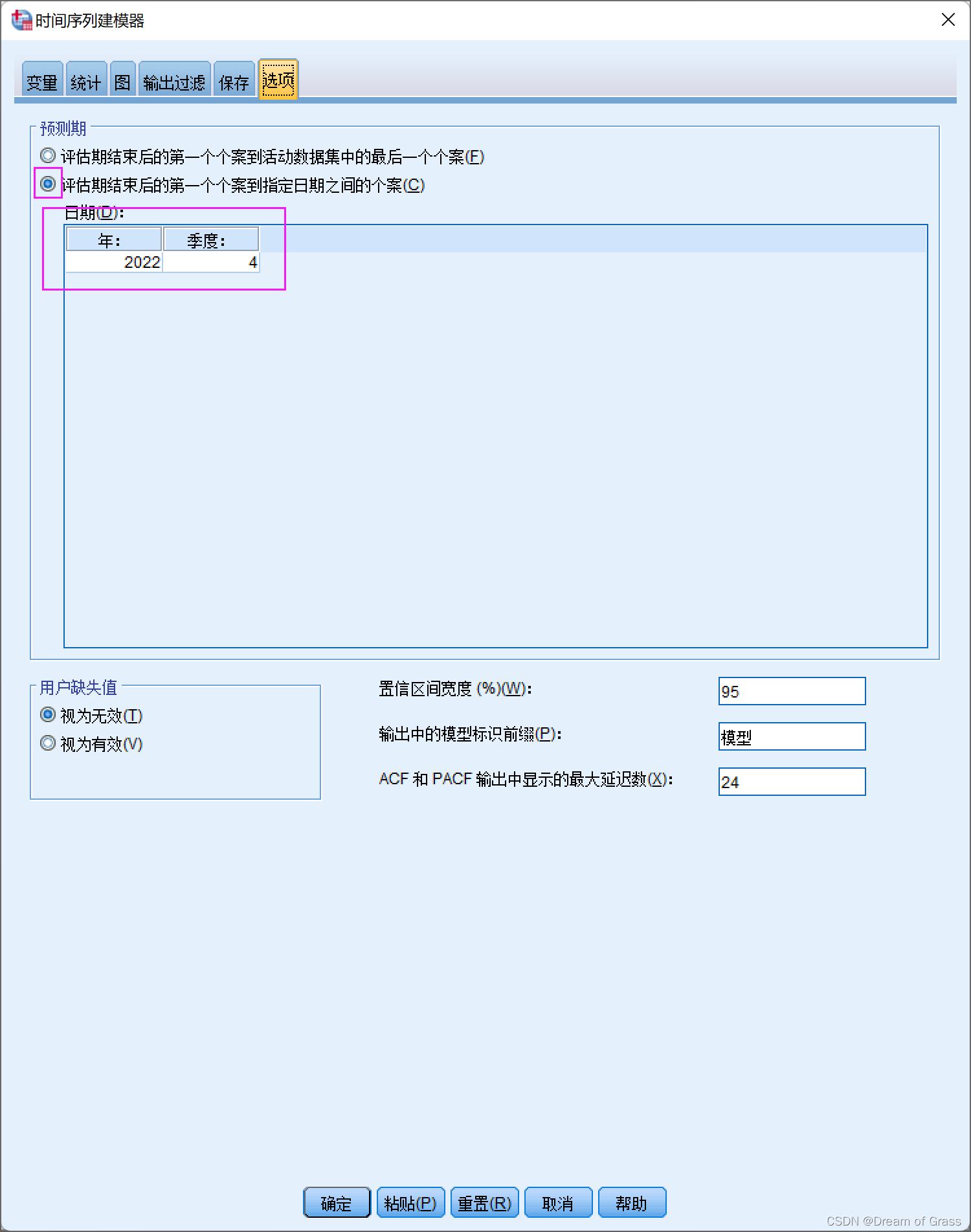
白噪声进行残差检验
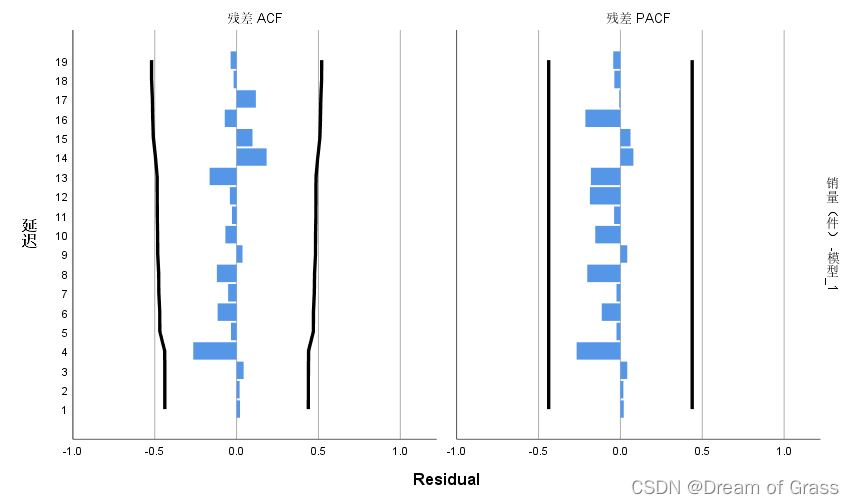
从残差的ACF和PACF冬形中可以看出,所有滞后阶数的自相关系数和偏自相关系数均和o没有显著的差异;
另外从下表可以看出,对残差进行Q检验得到的p值为0.741,即我们无法拒绝原假设,认为残差就是白噪声序列,因此温特加法模型能够很好的识别本例中的销量数据。

预测的结果和效果图
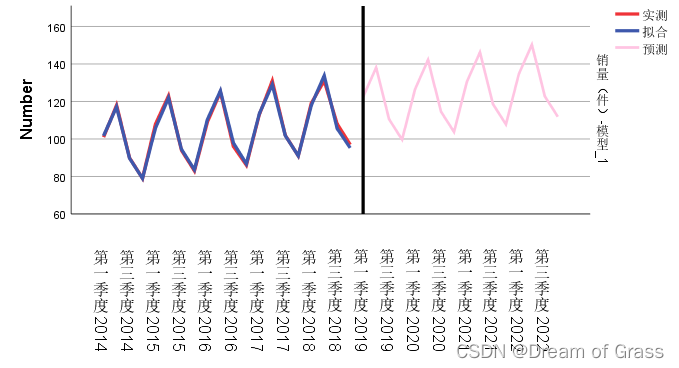
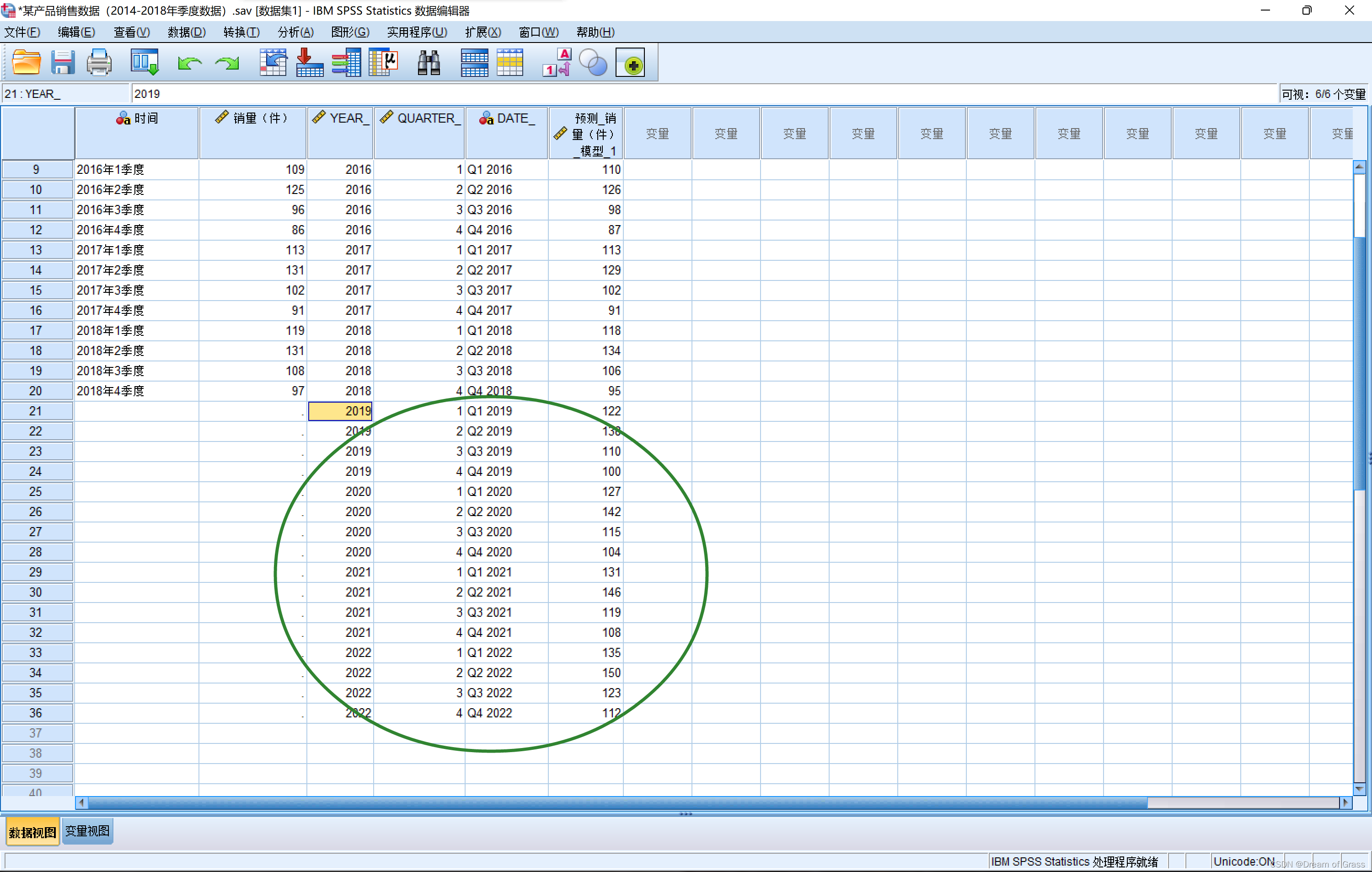
从图中可以看出,真实数据和拟合数据的时序图几乎重合,这说明温特加法模型对原数据拟合的效果很好;
另外,预测的后两年的数据既保留了原始序列的季节效应,也同时具有向上的线性趋势,这说明温特加法模型能很好的对该产品的销量数据进行预测。
人口数据预测
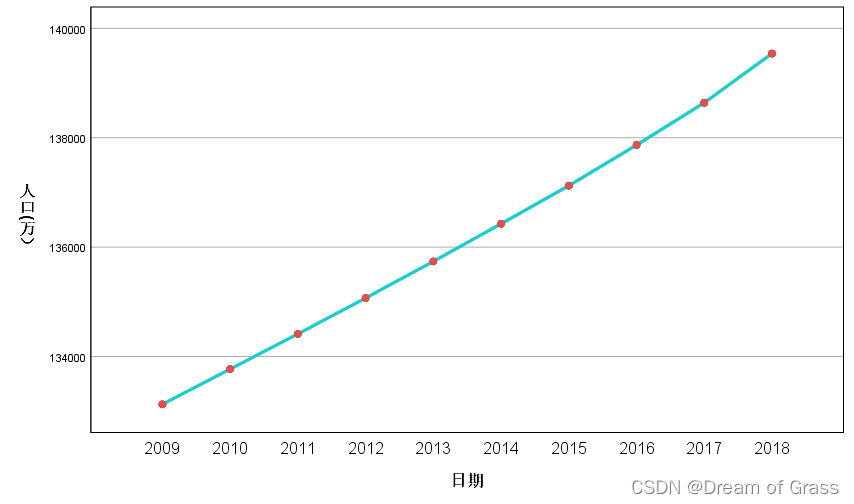
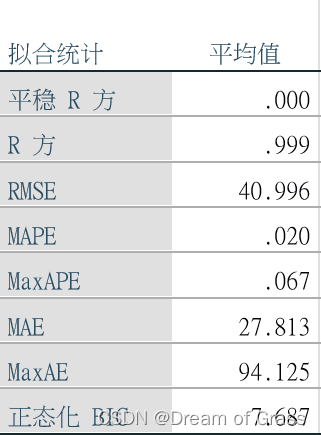
预测结果

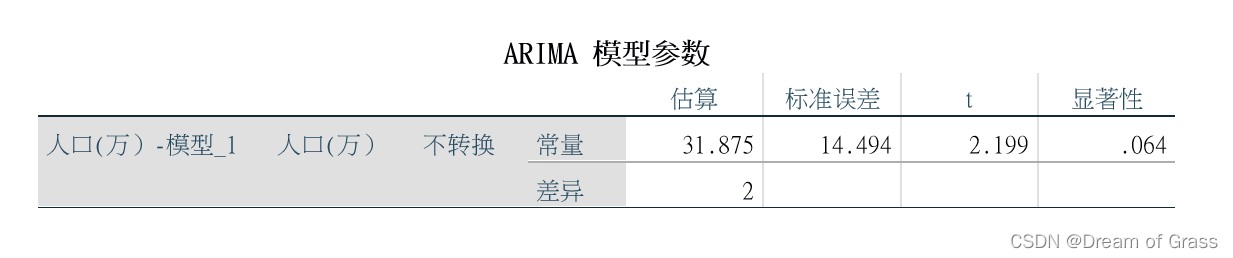

残差的白噪声检测
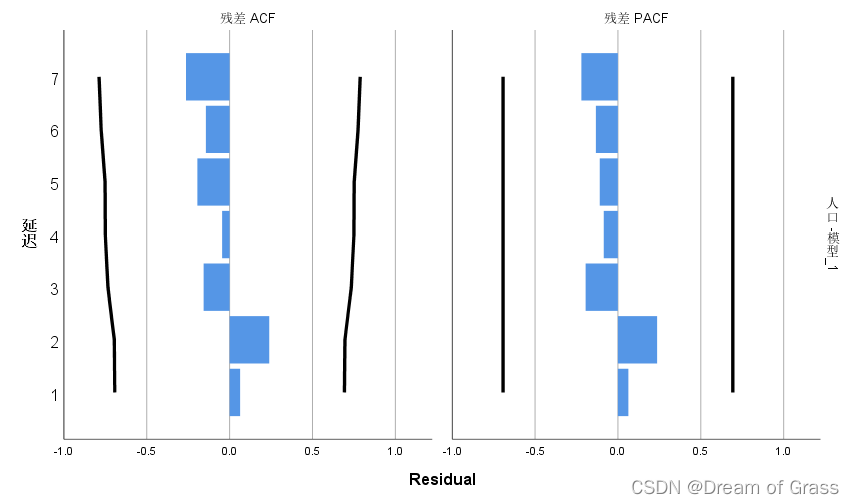

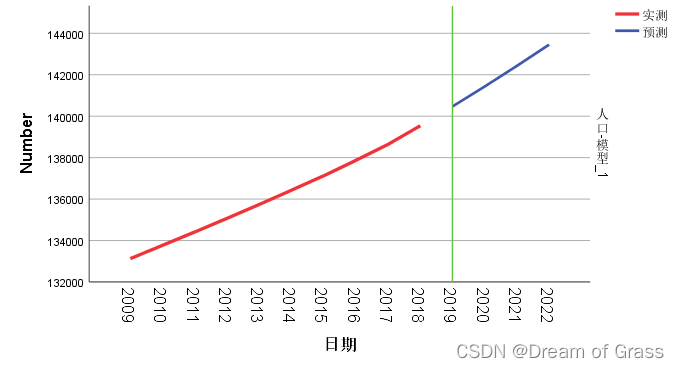
预测效果图形
上海证券交易所指数预测
给定2016/01/04至2019/08/07的上海证券交易所指数,请对其进行建模,并预测接下来一段时间的指数走势。
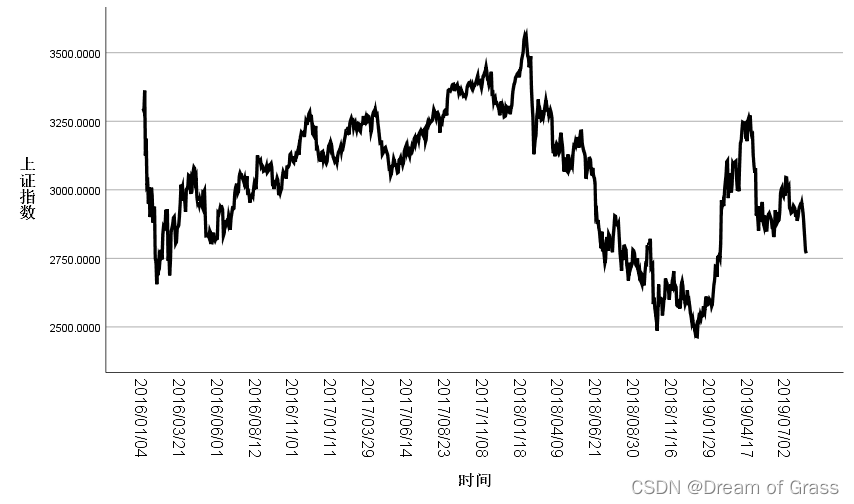
直接进行专家建模的结果

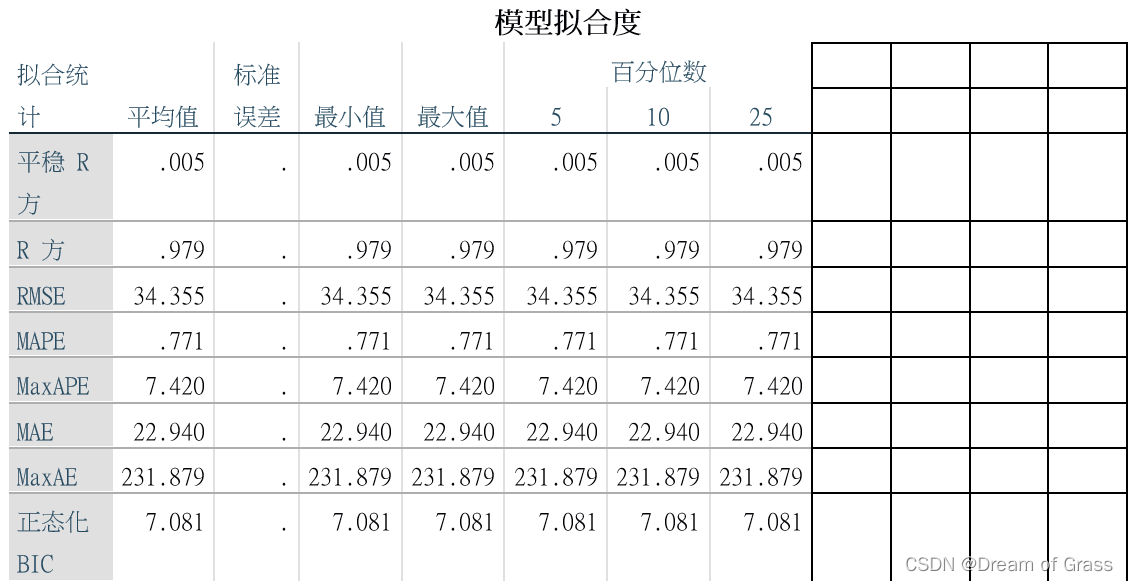
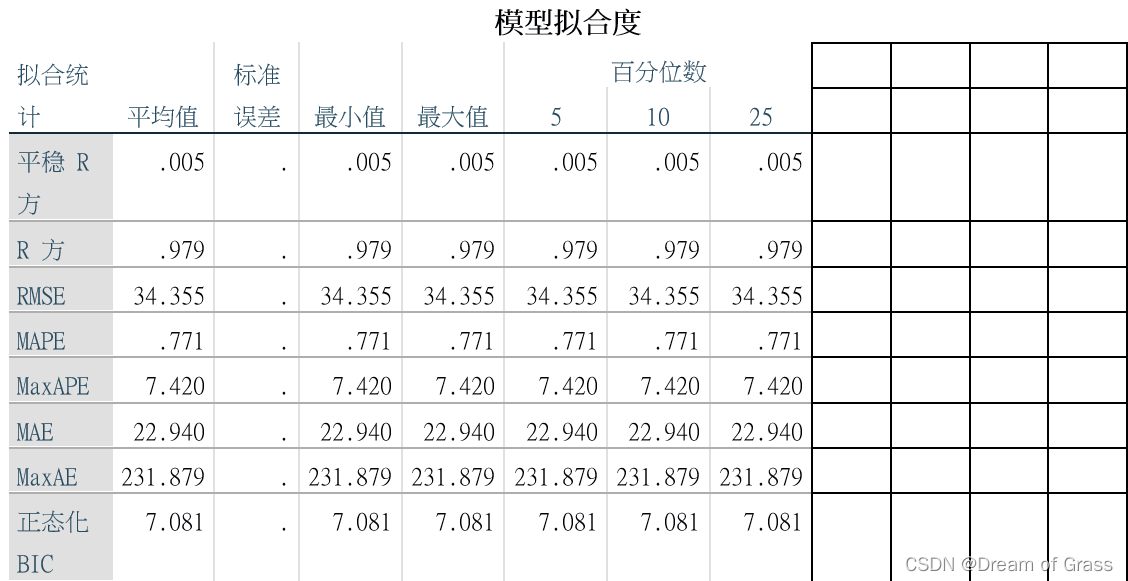


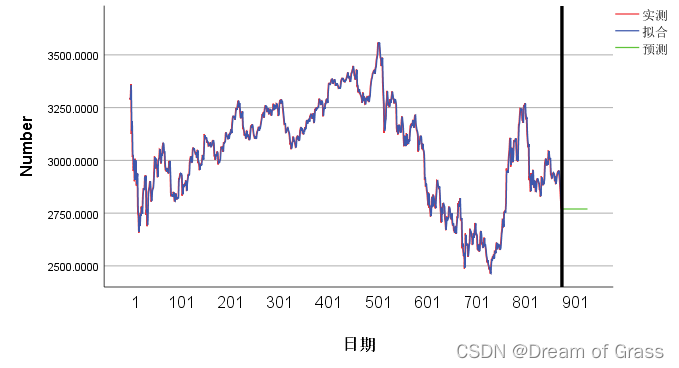
- 观察横坐标,Spss在建模时已经将我们的时间数据转换成了序列号了,这是因为我们的日期不连续导致的。
- R方很大说明拟合的很不错,但是平稳R方很小,且最关键的Q检验拒绝了原假设(认为残差不是白噪声,即模型没有完全识别出我们的数据),说明模型有待改进。
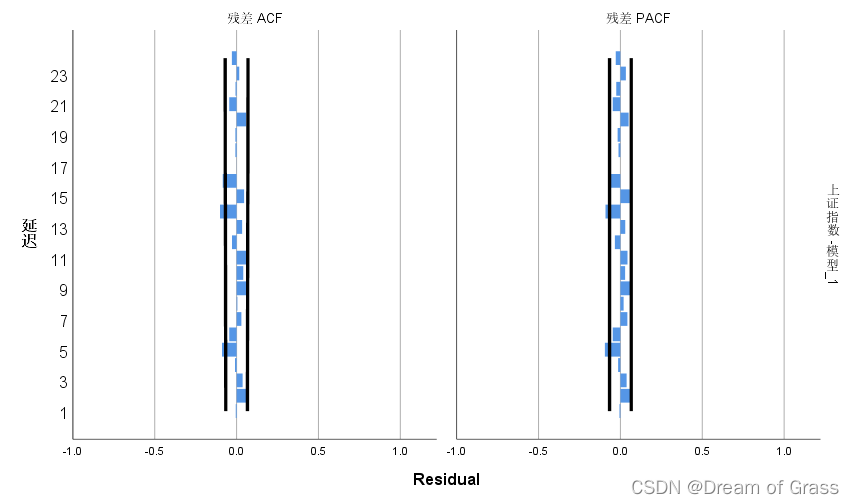
- 残差的ACF和PACF中有很多滞后阶数显著的异于0,说明残差不是白噪声;
- 简单指数平滑模型只能预测未来一期的哦。
剔除异常值后重新建模
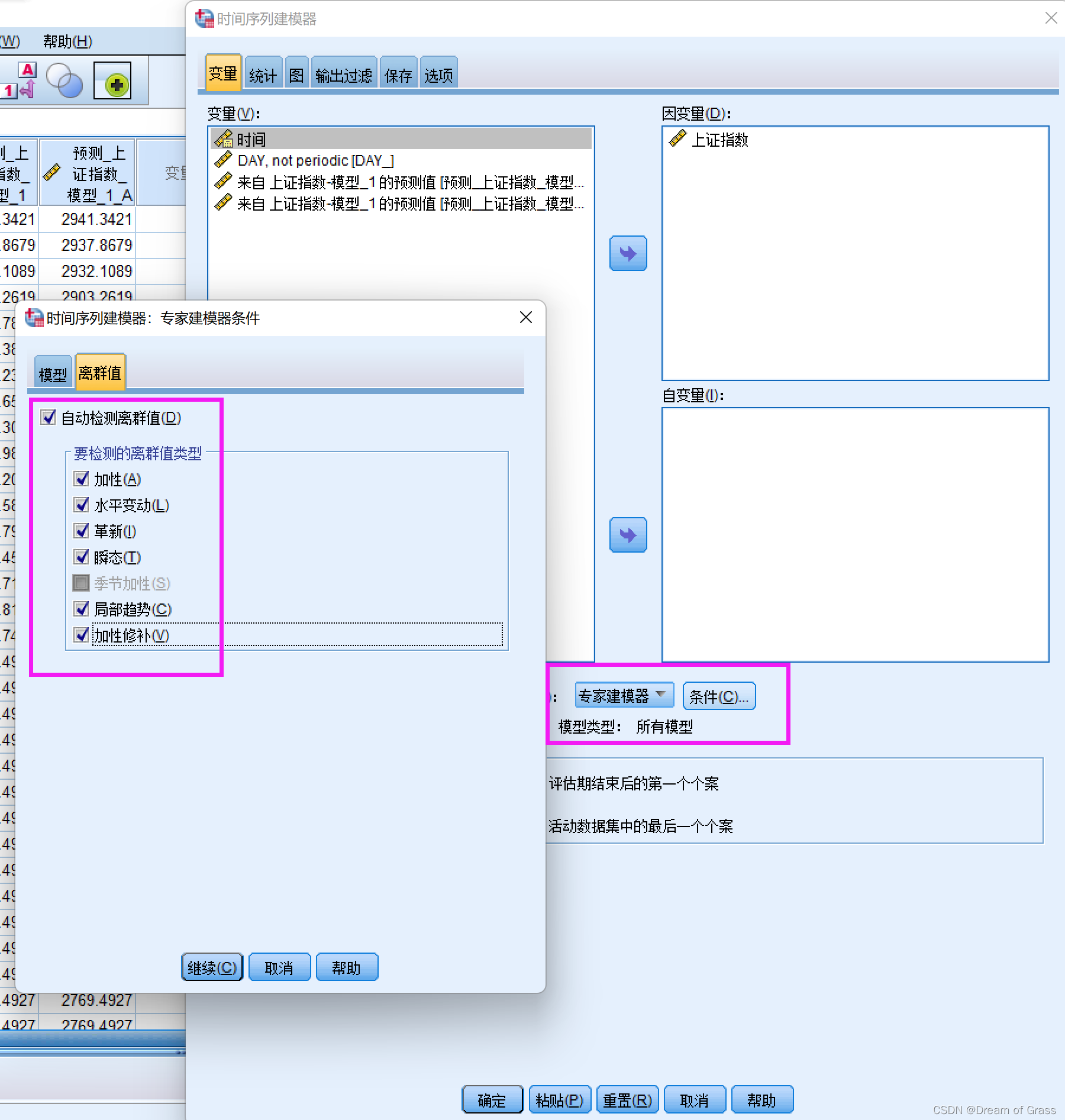
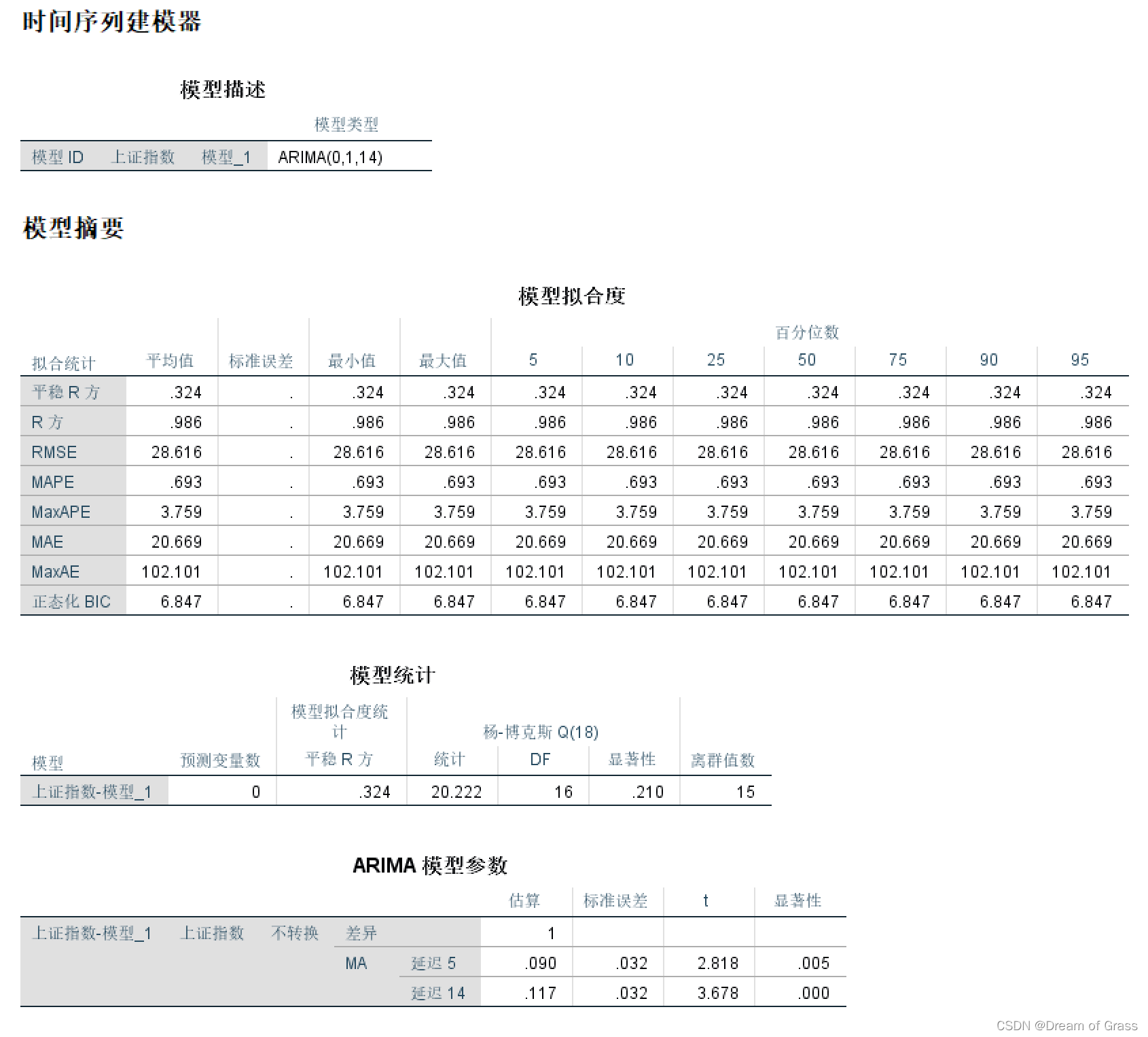
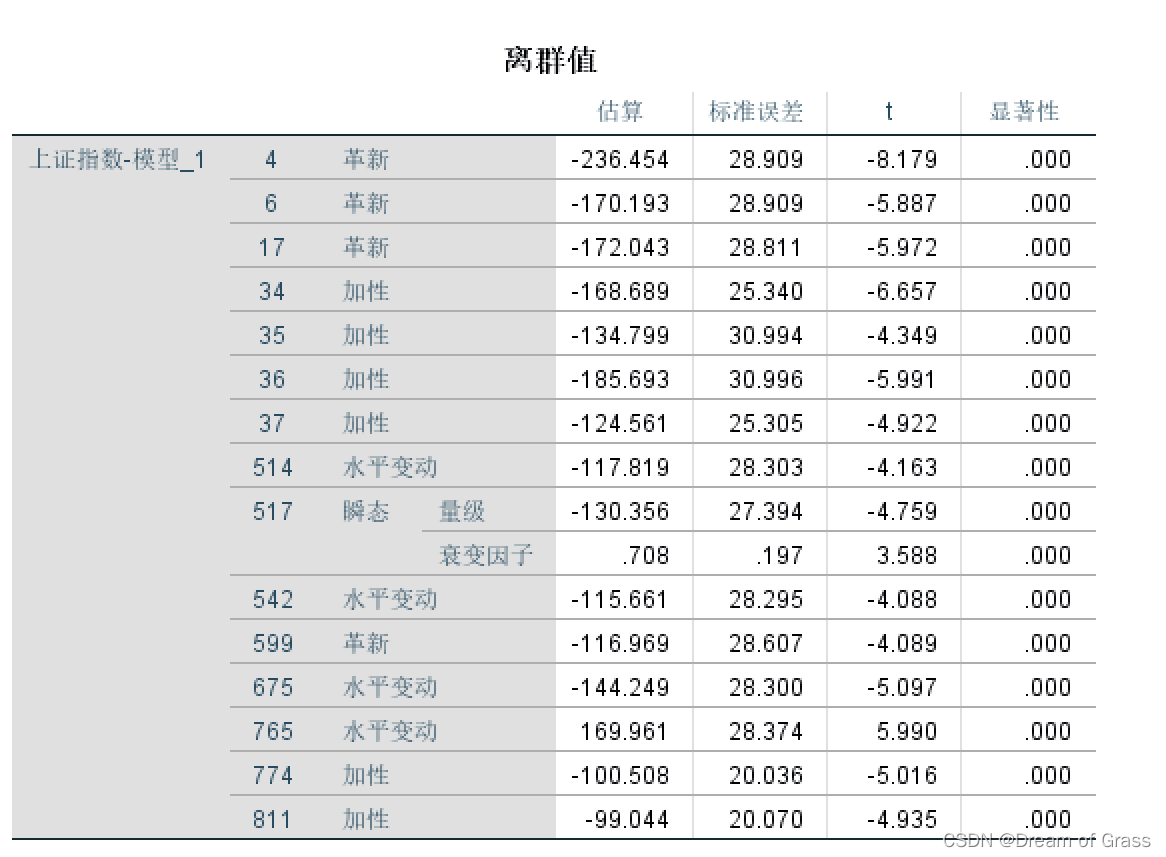
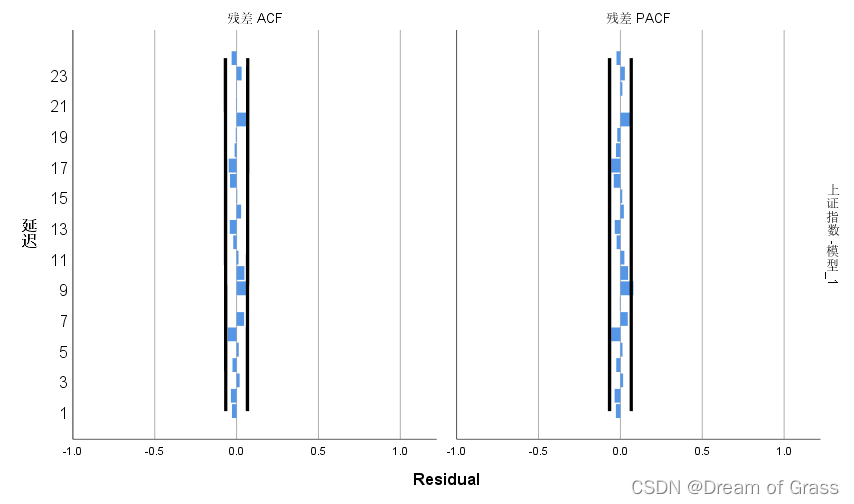
剔除异常值后, R 2 R^2 R2小幅增加,平稳的 R 2 R^2 R2明显增加,且残差也是白噪声了。
预测结果
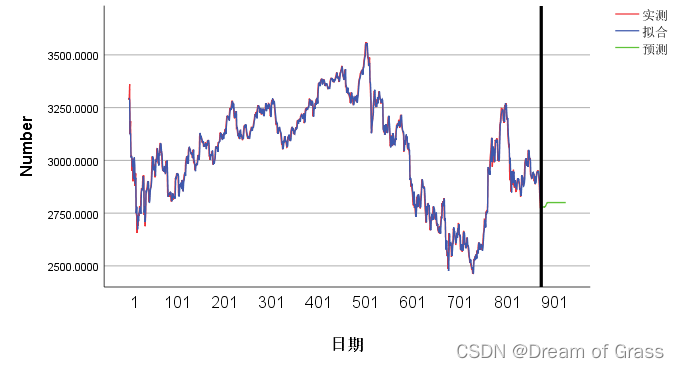
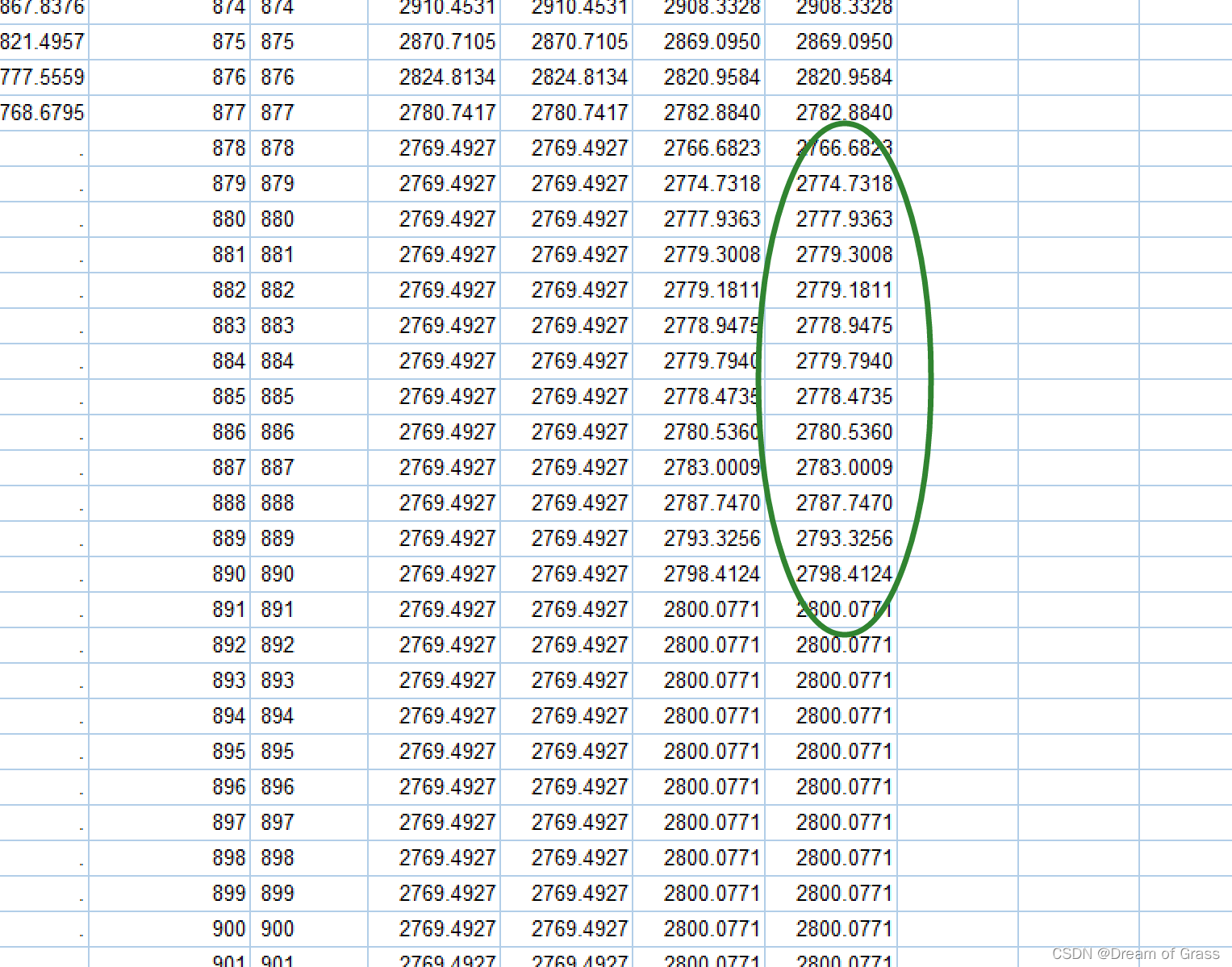
从表中可以看出,可以预测出前14期,超过14期后预测值不会改变哦~
GDP增速预测
真正的预测要结合背景,而不是直接套用模型,我们来看下面这个例子~
这个题目不能直接套模型,要结合背景


