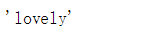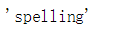- 1Win10系统下复现Pointnet++(pytorch)_pointnet++ windows上复现
- 2Streamlit自定义组件开发教程_streamlit教程
- 3stata处理wind数据——处理日期_stata数值型日期怎么提取年月日
- 4网络程序设计:基于Socket和epoll的网络聊天室_网络程序设计作业:基于socket api+epoll的在线聊天程序
- 5关于Django静态文件路径设置规则的精炼总结_django static文件规范
- 6python的nlargest_Python pandas.DataFrame.nlargest函数方法的使用
- 7微信小程序类目审核加急通道开放了
- 8[PCL]5 ICP算法进行点云匹配
- 9前端优化方案-CDN优化_前端cdn优化
- 10卷积神经网络之上采样-pytorch_卷积 上采样 pytorch
Python计算机视觉编程第八章——图像内容分类_如果需要进行文本识别,又要把图像分为
赞
踩
(一)K邻近分类法 (KNN)
基本思想:
把待分类文本表示成文本向量,与训练样本组成的样本空间中的向量计算相似度,得到k篇与该文本距离最近(最相似)的文本,根据这k篇文本所属的类别判定新文本所属的类别,在新文本的k个邻居中依次计算每类的权重,将文本分到权重最大的类中。
KNN 是非参数的(non-parametric),基于实例(instance-based)的算法。非参数意味着其不在底层的数据分布上进行任何的臆测。而基于实例意味着其不是明确地学习一个模型,而是选择记忆训练的实例们。由于 KNN 是基于实例的算法,也常被称呼为懒算法(lazy algorithm)。
算法原理:
当 KNN 被用于分类问题时,其输出是一个类别的成员(预测一个类别 - 一个离散值)
该算法包含三个元素:标记对象的集合(比如:一个分数记录的集合),对象之间的距离,k 的取值,即最邻近距离的数量。

我们将要把灰色的点分类为黄色,绿色,蓝色中的一类。一开始会计算灰色点与其他各个点的之间的距离,然后再找出 k 值 - 最邻近的一些点。

最邻近的点的数据按顺序如上所示,黄色的个数最多,所以灰色的点被划分为黄色所在的类。可以发现 KNN 是通过测量不同样本之间的距离进行分类的。KNN 算法的核心思想是:如果一个样本在特征空间中的 k 个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别。
算法步骤:
- 依公式计算 Item 与 D1、D2 … …、Dj 之相似度。得到Sim(Item, D1)、Sim(Item, D2)… …、Sim(Item, Dj)。
- 将Sim(Item, D1)、Sim(Item, D2)… …、Sim(Item, Dj)排序,若是超过相似度门槛t则放入邻居案例集合NN。
- 自邻居案例集合NN中取出前k名,依多数决,得到Item可能类别。
这种方法通常分类效果较好,但是也有很多弊端:与 K-means 聚类算法一样,需要预先设定 k 值,k 值的选择会影响分类的性能;此外,这种方法要求将整个训练集存储起来,如果训练集非常大,搜索起来就非常慢。对于大训练集,采取某些装箱形式通常会减少对比的次 数,从积极的一面来看,这种方法在采用何种距离度量方面是没有限制的;实际上, 对于你所能想到的东西它都可以奏效,但这并不意味着对任何东西它的分类性能都很好。另外,这种算法的可并行性也很一般。
实现最基本的 KNN 形式非常简单。给定训练样本集和对应的标记列表,下面的代码可以用来完成这一工作。这些训练样本和标记可以在一个数组里成行摆放或者干脆摆放列表里,训练样本可能是数字、字符串等任何你喜欢的形状。将定义的类对象添加到名为 knn.py 的文件里:
from numpy import * class KnnClassifier(object): def __init__(self,labels,samples): """ 使用训练数据初始化分类器 """ self.labels = labels self.samples = samples def classify(self,point,k=3): """ 在训练数据上采用 k 近邻分类,并返回标记 """ # 计算所有训练数据点的距离 dist = array([L2dist(point,s) for s in self.samples]) # 对它们进行排序 ndx = dist.argsort() # 用字典存储 k 近邻 votes = {} for i in range(k): label = self.labels[ndx[i]] votes.setdefault(label,0) votes[label] += 1 return max(votes) def L2dist(p1,p2): return sqrt( sum( (p1-p2)**2) ) def L1dist(v1,v2): return sum(abs(v1-v2))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
定义一个类并用训练数据初始化非常简单 ; 每次想对某些东西进行分类时,用 KNN 方法,我们就没有必要存储并将训练数据作为参数来传递。用一个字典来存储邻近标记,我们便可以用文本字符串或数字来表示标记。在这个例子中,我们用欧式距离 (L2) 进行度量,也可以使用其他度量方式,只需要将其作为函数添加到上面代码的最后。
一个简单的二维示例
首先建立一些简单的二维示例数据集来说明并可视化分类器的工作原理,下面的脚本将创建两个不同的二维点集,每个点集有两类,用 Pickle 模块来保存创建的数据:
# -*- coding: utf-8 -*- from numpy.random import randn import pickle from pylab import * # create sample data of 2D points # 创建二维样本数据 n = 200 # two normal distributions # 两个正态分布数据集 class_1 = 0.2 * randn(n, 2) class_2 = 1.6 * randn(n, 2) + array([5, 1]) labels = hstack((ones(n), -ones(n))) # save with Pickle # 用 Pickle 模块保存 # with open('points_normal.pkl', 'w') as f: with open('points_normal_test.pkl', 'wb') as f: pickle.dump(class_1, f) pickle.dump(class_2, f) pickle.dump(labels, f) # normal distribution and ring around it # 正态分布,并使数据成环绕状分布 print ("save OK!") class_1 = 0.6 * randn(n, 2) r = 0.8 * randn(n, 1) + 5 angle = 2 * pi * randn(n, 1) class_2 = hstack((r * cos(angle), r * sin(angle))) labels = hstack((ones(n), -ones(n))) # save with Pickle # 用 Pickle 保存 # with open('points_ring.pkl', 'w') as f: with open('points_ring_test.pkl', 'wb') as f: pickle.dump(class_1, f) pickle.dump(class_2, f) pickle.dump(labels, f)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
用不同的保存文件名运行该脚本两次,例如第一次用代码中的文件名进行保存,第二次将代码中的 points_normal_t.pkl 和 points_ring_t.pkl 分别改为 points_normal_test. pkl 和 points_ring_test.pkl 进行保存。将得到 4 个二维数据集文件(如下图所示),上述代码创建了两个不同的二维点集,每个点集有两类。
第一个二维点集中的class_1的数据集原本是200行2列的随机正态分布数据,之后将每个数据缩小了0.6倍。class_2的数据集原本是200行2列的随机正态分布数据,之后将每个数据扩大了1.2倍。
第二个二维点集中的class_1的数据集200行2列的随机正态分布数据,之后将每个数据缩小了0.2倍。class_2数据集是类似于长轴长度为2,短轴长度为根号2的椭圆的分布形状。
每个分布都有两个文件,将一个用来训练,另一个用来做测试。

用下面的代码来创建一个脚本:
# -*- coding: utf-8 -*- import pickle from pylab import * from PCV.classifiers import knn from PCV.tools import imtools # 用 Pickle 载入二维数据点 with open('points_normal_t.pkl','r') as f: class_1 = pickle.load(f) class_2 = pickle.load(f) labels = pickle.load(f) model = knn.KnnClassifier(labels, vstack((class_1, class_2))) # 用Pickle模块载入测试数据 with open('points_normal_test.pkl', 'r') as f: class_1 = pickle.load(f) class_2 = pickle.load(f) labels = pickle.load(f) #在测试数据集的第一个数据点上进行测试 print (model.classify(class_1[0])) #为了可视化所有测试数据点的分类,并展示分类器将两个不同的类分开得怎样,我 们可以添加这些代码: # 定义绘图函数 def classify(x,y,model=model): return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)]) # 绘制分类边界 imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1]) show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
创建了一个简短的辅助函数以获取 x 和 y 二维坐标数组和分类器,并返回一个预测的类标记数组。
def plot_2D_boundary(plot_range,points,decisionfcn,labels,values=[0]): """ Plot_range 为(xmin,xmax,ymin,ymax), points 是类数据点列表,decisionfcn 是评估函数,labels 是函数 decidionfcn 关于每个类返回的标记列表 """ clist = ['b','r','g','k','m','y'] # 不同的类用不同的颜色标识 # 在一个网格上进行评估,并画出决策函数的边界 x = arange(plot_range[0],plot_range[1],.1) y = arange(plot_range[2],plot_range[3],.1) xx,yy = meshgrid(x,y) xxx,yyy = xx.flatten(),yy.flatten() # 网格中的 x,y 坐标点列表 zz = array(decisionfcn(xxx,yyy)) zz = zz.reshape(xx.shape) # plot contour(s) at values contour(xx,yy,zz,values) #对于每类,用 * 画出分类正确的点,用 o 画出分类不正确的点 for i in range(len(points)): d = decisionfcn(points[i][:,0],points[i][:,1]) correct_ndx = labels[i]==d incorrect_ndx = labels[i]!=d plot(points[i][correct_ndx,0],points[i][correct_ndx,1],'*',color=clist[i]) plot(points[i][incorrect_ndx,0],points[i][incorrect_ndx,1],'o',color=clist[i]) axis('equal')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
当n=200 k=3时:

当n=20 k=3时:

每个示例中,不同颜色代表类标记,正确分类的点用星号表示,分类错误的点用圆点表示,曲线是分类器的决策边界。正如所看到的,kNN 决策边界适用于没有任何明确模型的类分布。
用稠密 SIFT 作为图像特征
在整幅图像上用一个规则的网格应用 SIFT 描述子可以得到稠密 SIFT 的表示形式 ,
from PIL import Image import os from numpy import * import sift def process_image_dsift(imagename,resultname,size=20,steps=10,force_orientation=False,resize=None): """ 用密集采样的 SIFT 描述子处理一幅图像,并将结果保存在一个文件中。可选的输入: 特征的大小 size,位置之间的步长 steps,是否强迫计算描述子的方位 force_orientation (False 表示所有的方位都是朝上的),用于调整图像大小的元组 """ im = Image.open(imagename).convert('L') if resize!=None: im = im.resize(resize) m,n = im.size if imagename[-3:] != 'pgm': #创建一个 pgm 文件 im.save('tmp.pgm') imagename = 'tmp.pgm' # 创建帧,并保存到临时文件 scale = size/3.0 x,y = meshgrid(range(steps,m,steps),range(steps,n,steps)) xx,yy = x.flatten(),y.flatten() frame = array([xx,yy,scale*ones(xx.shape[0]),zeros(xx.shape[0])]) savetxt('tmp.frame',frame.T,fmt='%03.3f') if force_orientation: cmmd = str("sift "+imagename+" --output="+resultname+ " --read-frames=tmp.frame --orientations") else: cmmd = str("sift "+imagename+" --output="+resultname+ " --read-frames=tmp.frame") os.system(cmmd) print 'processed', imagename, 'to', resultname
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
为了使用命令行处理,用 savetxt() 函数将帧数组存储在一个文本文件中,该函数的最后一个参数可以在提取描述子之前对 图像的大小进行调整,例如,传递参数 imsize=(100, 100) 会将图像调整为 100×100 像素的方形图像。最后,如果 force_orientation 为真,则提取出来的描述子会基于局部主梯度方向进行归一化;否则,则所有的描述子的方向只是简单地朝上。
利用类似下面的代码可以计算稠密 SIFT 描述子,并可视化它们的位置:
# -*- coding: utf-8 -*-
import sift, dsift
from pylab import *
from PIL import Image
dsift.process_image_dsift('D:\\Python\\chapter8\\empire.jpg','D:\\Python\\chapter7\\empire.sift',90,40,True)
l,d = sift.read_features_from_file('D:\\Python\\chapter8\\empire.sift')
im = array(Image.open('D:\\Python\\chapter8\\empire.jpg'))
sift.plot_features(im,l,True)
show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
代码里面的90,40分别代表圆圈的大小和圆心间隔,可以修改参数调节大小。
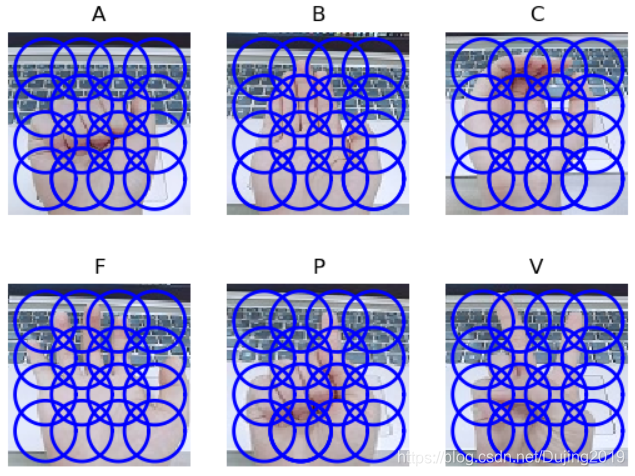
图像分类:手势识别
用稠密 SIFT 描述子来表示这些手势图像,将图像放在一个名为 uniform 的文件夹 里,每一类均分两组,并分别放入名为 train 和 test 的两个文件夹中。
可以通过下面的代码得到每幅图像的稠密 SIFT 特征:
import dsift
# 将图像尺寸调为 (50,50),然后进行处理
for filename in
imlist: featfile = filename[:-3]+'dsift' dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))
- 1
- 2
- 3
- 4
上面代码会对每一幅图像创建一个特征文件,文件名后缀为 .dsift。
注意:这里将图像分辨率调成了常见的固定大小。这是非常重要的,否则这些图像会有不同数量的描述子,从而每幅图像的特征向量长度也不一样,这将导致在后面比较它们时出错。
定义一个辅助函数,用于从文件中读取稠密 SIFT 描述子,如下:
# -*- coding: utf-8 -*- from PCV.localdescriptors import dsift import os from PCV.localdescriptors import sift from pylab import * from PCV.classifiers import knn def get_imagelist(path): return [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.ppm')] def read_gesture_features_labels(path): """ 对所有以 .dsift 为后缀的文件创建一个列表. """ featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')] # 读取特征 features = [] for featfile in featlist: l,d = sift.read_features_from_file(featfile) features.append(d.flatten()) features = array(features) # 创建标记 labels = [featfile.split('/')[-1][0] for featfile in featlist] return features,array(labels) #读取训练集、测试集的特征和标记信息 features,labels = read_gesture_features_labels('D:\\Python\\chapter8\\train\\') test_features,test_labels = read_gesture_features_labels('D:\\Python\\chapter8\\test\\') classnames = unique(labels) # 测试 kNN k = 1 knn_classifier = knn.KnnClassifier(labels,features) res = array([knn_classifier.classify(test_features[i],k) for i in range(len(test_labels))]) # 准确率 acc = sum(1.0*(res==test_labels)) / len(test_labels) print ('Accuracy:', acc)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
首先,用训练数据及其标记作为输入,创建分类器对象;然后,我们在整个测试集上遍历并用 classify() 方法对每幅图像进行分类。将布尔数组和 1 相乘并求和,可以计算出分类的正确率。由于该例中真值为 1,所以很容易计算出正确分类数。理论上应该会打印出一个类似下面的结果:
Accuracy: 0.811518324607
训练集和测试集完全相同会打印
但是训练集和测试集完全不相同也会打印
期间换了各种手势图片以及K值依旧如此,如果有博主知道原因,可以解答一下这个现象,谢谢!
(二)贝叶斯分类器
贝叶斯分类器是一种基于贝叶斯条件概率定理的概率分类器,它假设特征是彼此独立不相关的 (这就是它“朴素”的部分)。贝叶斯分类器可以非常有效地被训练出来,原因在于每一个特征模型都是独立选取的。尽管它们的假设非常简单,但是贝叶斯分类器已经在实际应用中获得显著成效,尤其是对垃圾邮件的过滤。
贝叶斯公式
P ( A ∣ B ) = P ( B / A ) P ( A ) P ( B ) P(A|B)=\frac{P(B/A)P(A)}{P(B)} P(A∣B)=P(B)P(B/A)P(A)
拼写纠错实例:
问题:我们看到用户输入了一个不在字典中的单词,我们需要去猜测,用户真正想输入的单词是什么?
-
转换成数学语言:
P(我们猜测他想输入的单词 | 他实际输入的单词 ) -
假设用户实际输入的单词记为D(D代表data,即为观测数据)
-
猜测1: P ( h 1 ∣ D ) P(h1 | D) P(h1∣D),猜测2: P ( h 2 ∣ D ) P(h2 | D) P(h2∣D),猜测3: P ( h 3 ∣ D ) P(h3 | D) P(h3∣D)…统一为: P ( h ∣ D ) P(h | D) P(h∣D)
P ( h ∣ D ) = P ( D ∣ h ) ∗ P ( h ) / P ( D ) P(h|D)=P(D|h)*P(h)/P(D) P(h∣D)=P(D∣h)∗P(h)/P(D) -
对于不同的具体猜测 h 1 , h 2 , h 3.... p ( D ) h1,h2,h3....p(D) h1,h2,h3....p(D)都是一样的,所以在比较 P ( h 1 ∣ D ) P(h1|D) P(h1∣D)和 P ( h 2 ∣ D ) P(h2|D) P(h2∣D)的时候我们可以忽略这个常数。则 P ( h ∣ D ) P(h|D) P(h∣D)正比于 P ( D ∣ h ) ∗ P ( h ) P(D|h)*P(h) P(D∣h)∗P(h)
-
对于给定观测数据,一个猜测是好是坏,取决于“这个猜测本身独立的可能性大小(先验概率,Prior)” 和 “这个猜测生成我们观测到的数据的可能性大小”
-
贝叶斯方法计算: P ( D ∣ h ) ∗ P ( h ) P(D|h)*P(h) P(D∣h)∗P(h), P ( h ) P(h) P(h)是特定猜测的先验概率。比如用户输入tIp,那到底是top还是tip,这个时候,当最大似然(最符合观测数据的(即 P ( D ∣ h ) P(D|h) P(D∣h)最大的)最有优势。)不能做出决定性的判断时,先验概率就可以给出指示,一般来说top出现的程度要高许多,所以他更可能打的是top。
贝叶斯拼写检查器
它以一个单词作为输入参数, 返回最可能的拼写建议结果
import re, collections # 把语料中的单词全部抽取出来, 转成小写, 并且去除单词中间的特殊符号 def words(text): return re.findall('[a-z]+', text.lower()) def train(features): model = collections.defaultdict(lambda: 1) for f in features: model[f] += 1 return model NWORDS = train(words(open(r'D:\\Python\\chapter8\\big.txt').read())) alphabet = 'abcdefghijklmnopqrstuvwxyz' #返回所有与单词 w 编辑距离为 1 的集合 def edits1(word): n = len(word) return set([word[0:i]+word[i+1:] for i in range(n)] + # deletion [word[0:i]+word[i+1]+word[i]+word[i+2:] for i in range(n-1)] + # transposition [word[0:i]+c+word[i+1:] for i in range(n) for c in alphabet] + # alteration [word[0:i]+c+word[i:] for i in range(n+1) for c in alphabet]) # insertion #返回所有与单词 w 编辑距离为 2 的集合 #在这些编辑距离小于2的词中间, 只把那些正确的词作为候选词 def known_edits2(word): return set(e2 for e1 in edits1(word) for e2 in edits1(e1) if e2 in NWORDS) def known(words): return set(w for w in words if w in NWORDS) #如果known(set)非空, candidate 就会选取这个集合, 而不继续计算后面的 def correct(word): candidates = known([word]) or known(edits1(word)) or known_edits2(word) or [word] return max(candidates, key=lambda w: NWORDS[w]) correct('lovele') #correct('speling')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
代码运行结果:
垃圾邮件过滤实例:
问题:给定一封邮件,判定它是否属于垃圾邮件?
-
D D D来表示这封邮件,由 N N N个单词组成。用 S S S表示垃圾邮件, H H H表示正常邮件。
P ( S ∣ D ) = P ( S ) ∗ P ( D ∣ S ) / P ( D ) P(S|D)=P(S)*P(D|S)/P(D) P(S∣D)=P(S)∗P(D∣S)/P(D) P ( H ∣ D ) = P ( H ) ∗ P ( D ∣ H ) / P ( D ) P(H|D)=P(H)*P(D|H)/P(D) P(H∣D)=P(H)∗P(D∣H)/P(D) -
先验概率: P ( S ) P(S) P(S)和 P ( H ) P(H) P(H)这两个先验概率都是很容易求出来的,只需要计算一个邮件库里面垃圾邮件和正常邮件的比例就行了。
-
D D D 里面含有 N N N个单词 d 1 , d 2 , d 3... d1, d2, d3... d1,d2,d3... P ( D ∣ S ) = P ( d 1 , d 2 , … , d n ∣ S ) P(D|S) = P(d1,d2,…,dn|S) P(D∣S)=P(d1,d2,…,dn∣S), P ( d 1 , d 2 , … , d n ∣ S ) P(d1,d2,…,dn|S) P(d1,d2,…,dn∣S) 就是说在垃圾邮件当中出现跟我们目前这封邮件一模一样的一封邮件的概率是多大。
-
P ( d 1 , d 2 , … , d n ∣ S ) P(d1,d2,…,dn|S) P(d1,d2,…,dn∣S) 扩展为: P ( d 1 ∣ S ) ∗ P ( d 2 ∣ d 1 , S ) ∗ P ( d 3 ∣ d 2 , d 1 , S ) ∗ … P(d1|S) * P(d2|d1, S) * P(d3|d2,d1, S) * … P(d1∣S)∗P(d2∣d1,S)∗P(d3∣d2,d1,S)∗…
-
假设 d i di di与 d i − 1 d_{i-1} di−1 是完全条件无关的(朴素贝叶斯假设特征之间是独立,互不影响),实际上 d 1 , d 2 , d 3 , d 4... d1,d2,d3,d4... d1,d2,d3,d4...是相关的,但是为了求解,不得不这样做,而且会对结果造成影响,但是对结果的影响没那么高,也能帮我们把解求出来,是我们可以接受的。简化为 P ( d 1 ∣ S ) ∗ P ( d 2 ∣ S ) ∗ P ( d 3 ∣ S ) ∗ … P(d1|S) * P(d2|S) * P(d3|S) * … P(d1∣S)∗P(d2∣S)∗P(d3∣S)∗…
-
对于 P ( d 1 ∣ S ) ∗ P ( d 2 ∣ S ) ∗ P ( d 3 ∣ S ) ∗ … P(d1|S) * P(d2|S) * P(d3|S) * … P(d1∣S)∗P(d2∣S)∗P(d3∣S)∗…只要统计 d i di di 这个单词在垃圾邮件中出现的频率即可。
贝叶斯过滤器:
贝叶斯过滤器是一种统计学过滤器,建立在已有的统计结果之上。还是以邮件过滤为例,我们必须预先提供两组已经识别好的邮件,一组是正常邮件,另一组是垃圾邮件。我们用这两组邮件,对过滤器进行"训练"。这两组邮件的规模越大,训练效果就越好。
"训练"过程很简单。首先,解析所有邮件,提取每一个词。然后,计算每个词语在正常邮件和垃圾邮件中的出现频率。比如,我们假定"advertisement"这个词,在4000封垃圾邮件中,有200封包含这个词,那么它的出现频率就是5%;而在4000封正常邮件中,只有2封包含这个词,那么出现频率就是0.05%。
假设我们收到了一封新邮件。在未经统计分析之前,我们假定它是垃圾邮件的概率为50%。因此P(S)和P(H)的先验概率都是50%。
即
p
(
S
)
=
p
(
H
)
=
50
%
p(S)=p(H)=50\%
p(S)=p(H)=50%
然后,对这封邮件进行解析,发现其中包含了advertisement这个词,用A表示这个单词,那么问题就变成了计算P(S|A)的值,即在某个词语(A)已经存在的条件下,垃圾邮件(S)的概率有多大。
根据条件概率公式,可以写出:
P
(
S
∣
A
)
=
P
(
A
∣
S
)
P
(
S
)
P
(
A
∣
S
)
P
(
S
)
+
P
(
A
∣
H
)
P
(
H
)
P(S|A)=\frac{P(A|S)P(S)}{P(A|S)P(S)+P(A|H)P(H)}
P(S∣A)=P(A∣S)P(S)+P(A∣H)P(H)P(A∣S)P(S)
公式中,P(A|S)和P(A|H)的含义是,这个词语在垃圾邮件和正常邮件中,分别出现的概率。分别等于5%和0.05%。所以,马可以计算P(S|A)的值:
P
(
S
∣
W
)
=
5
%
×
50
%
5
%
×
50
%
+
0.05
%
×
50
%
=
99.0
%
P(S|W)=\frac{5\%\times 50\%}{5\%\times 50\%+0.05\%\times 50\%}=99.0\%
P(S∣W)=5%×50%+0.05%×50%5%×50%=99.0%
这封新邮件是垃圾邮件的概率等于99%。这说明,advertisement这个词的推断能力很强,将50%的"先验概率"一下子提高到了99%的"后验概率"。
但是我们仍然不能得到这封邮件就是垃圾邮件,因为一封邮件包含很多词语,一些词语(比如advertisement)认定这是垃圾邮件,另一些认定不是。
现在就是计算联合概率(多个事件发生的情况下,另一个事件发生的概率有多大),比如:已知W1和W2是两个不同的词语,它们都出现在某封电子邮件之中,那么这封邮件是垃圾邮件的概率,就是联合概率。而结果就是两种,垃圾邮件(事件E1)或正常邮件(事件E2)。
| 事件 | W1 | W2 | 垃圾邮件 |
|---|---|---|---|
| E1 | 出现 | 出现 | Yes |
| E2 | 出现 | 出现 | No |
假设事件独立
概率分布如下:
| 事件 | W1 | W2 | 垃圾邮件 |
|---|---|---|---|
| E1 | P(S|W1) | P(S|W2) | P(S ) |
| E2 | 1-P(S|W1) | 1-P(S|W2) | 1-P(S) |
则:
P
(
E
1
)
=
P
(
S
∣
W
1
)
P
(
S
∣
W
2
)
P
(
S
)
P(E_{1})=P(S|W_{1})P(S|W_{2})P(S)
P(E1)=P(S∣W1)P(S∣W2)P(S)
P
(
E
2
)
=
(
1
−
P
(
S
∣
W
1
)
)
(
1
−
P
(
S
∣
W
2
)
)
(
1
−
P
(
S
)
)
P(E_{2})=(1-P(S|W_{1}))(1-P(S|W_{2}))(1-P(S))
P(E2)=(1−P(S∣W1))(1−P(S∣W2))(1−P(S))
则垃圾邮件概率:
P
=
P
(
E
1
)
P
(
E
1
)
+
P
(
E
2
)
P=\frac{P(E_{1})}{P(E_{1})+P(E_{2})}
P=P(E1)+P(E2)P(E1)
即: P = P ( S ∣ W 1 ) P ( S ∣ W 2 ) P ( S ) P ( S ∣ W 1 ) P ( S ∣ W 2 ) P ( S ) + ( 1 − P ( S ∣ W 1 ) ) ( 1 − P ( S ∣ W 2 ) ) ( 1 − P ( S ) ) P=\frac{P(S|W_{1})P(S|W_{2})P(S)}{P(S|W_{1})P(S|W_{2})P(S)+(1-P(S|W_{1}))(1-P(S|W_{2}))(1-P(S))} P=P(S∣W1)P(S∣W2)P(S)+(1−P(S∣W1))(1−P(S∣W2))(1−P(S))P(S∣W1)P(S∣W2)P(S)
因为P(S)=0.5
P
=
P
(
S
∣
W
1
)
P
(
S
∣
W
2
)
P
(
S
∣
W
1
)
P
(
S
∣
W
2
)
+
(
1
−
P
(
S
∣
W
1
)
)
(
1
−
P
(
S
∣
W
2
)
)
P=\frac{P(S|W_{1})P(S|W_{2})}{P(S|W_{1})P(S|W_{2})+(1-P(S|W_{1}))(1-P(S|W_{2}))}
P=P(S∣W1)P(S∣W2)+(1−P(S∣W1))(1−P(S∣W2))P(S∣W1)P(S∣W2)
将
P
(
S
∣
W
1
)
P(S|W_{1})
P(S∣W1)记为
P
1
P_{1}
P1,
P
(
S
∣
W
2
)
P(S|W_{2})
P(S∣W2)记为
P
2
P_{2}
P2,即:
P
=
P
1
P
2
P
1
P
2
+
(
1
−
P
1
)
(
1
−
P
2
)
P=\frac{P_{1}P_{2}}{P_{1}P_{2}+(1-P_{1})(1-P_{2})}
P=P1P2+(1−P1)(1−P2)P1P2
当有n个词联合认定时:
P
=
P
1
P
2
.
.
.
P
n
P
1
P
2
.
.
.
P
n
+
(
1
−
P
1
)
(
1
−
P
2
.
.
.
(
1
−
P
n
)
P=\frac{P_{1}P_{2}...P_{n}}{P_{1}P_{2}...P{n}+(1-P_{1})(1-P_{2}...(1-P_{n})}
P=P1P2...Pn+(1−P1)(1−P2...(1−Pn)P1P2...Pn
这时候还需要一个门槛值,假设为0.9,则当概率大于90%以上,就认定为垃圾邮件,这时候即使一封正常邮件中出现advertisement,也不会被认定为垃圾邮件。
下面让我们看一个使用高斯概率分布模型的贝叶斯分类器基本实现,也就是用从训练数据集计算得到的特征均值和方差来对每个特征单独建模。把下面的Bayes Classifier 类添加到文件 bayes.py 中:
class BayesClassifier(object): def __init__(self): """使用训练数据初始化分类器 """ self.labels = [] # class labels self.mean = [] # class mean self.var = [] # class variances self.n = 0 # nbr of classes def train(self,data,labels=None): """ 在数据 data( n ×dim 的数组列表)上训练,标记 labels 是可选的,默认为 0… n -1 """ if labels==None: labels = range(len(data)) self.labels = labels self.n = len(labels) for c in data: self.mean.append(mean(c,axis=0)) self.var.append(var(c,axis=0)) def classify(self,points): """ 通过计算得出的每一类的概率对数据点进行分类,并返回最可能的标记 """ # 计算每一类的概率 est_prob = array([gauss(m,v,points) for m,v in zip(self.mean,self.var)]) print 'est prob',est_prob.shape,self.labels # 获取具有最高概率的索引,该索引会给出类标签 ndx = est_prob.argmax(axis=0) est_labels = array([self.labels[n] for n in ndx]) return est_labels, est_prob
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
该模型每一类都有两个变量,即类均值和协方差。train() 方法获取特征数组列表 (每个类对应一个特征数组),并计算每个特征数组的均值和协方差。classify() 方 法计算数据点构成的数组的类概率,并选概率最高的那个类,最终返回预测的类标记及概率值,同时需要一个高斯辅助函数
def gauss(m,v,x): """ 用独立均值 m 和方差 v 评估 d 维高斯分布 """ if len(x.shape)==1: n,d = 1,x.shape[0] else: n,d = x.shape # 协方差矩阵,减去均值 S = diag(1/v) x = x-m # 概率的乘积 y = exp(-0.5*diag(dot(x,dot(S,x.T)))) # 归一化并返回 return y * (2*pi)**(-d/2.0) / ( sqrt(prod(v)) + 1e-6)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
该函数用来计算单个高斯分布的乘积,返回给定一组模型参数m 和 v 的概率。
将该贝叶斯分类器用于上一节的二维数据,下面的脚本将载入上一节中的二维数据, 并训练出一个分类器:
# -*- coding: utf-8 -*- import pickle import bayes import matplotlib.pyplot as plt import imtools import numpy as np # 用 Pickle 模块载入二维样本点 with open('points_normal_t.pkl', 'r') as f: class_1 = pickle.load(f) class_2 = pickle.load(f) labels = pickle.load(f) # 训练贝叶斯分类器 bc = bayes.BayesClassifier() bc.train([class_1,class_2],[1,-1]) # 用 Pickle 模块载入测试数据 with open('points_normal_test.pkl', 'r') as f: class_1 = pickle.load(f) class_2 = pickle.load(f) labels = pickle.load(f) # 在某些数据点上进行测试 print bc.classify(class_1[:10])[0] # 绘制这些二维数据点及决策边界 def classify(x,y,bc=bc): points = vstack((x,y)) return bc.classify(points.T)[0]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
该脚本会将前 10 个二维数据点的分类结果打印输出到控制台,输出结果如下:
[1 1 1 1 1 1 1 1 1 1]
根据朴素贝叶斯分类函数分别计算待分类文档属于类1和类0的概率
现在将每个词的出现与否作为一个特征,这被描述为词集模型,但一个词在文档中出现不止一次,就要使用词袋模型,在词袋中,每个单词可以出现多次:
# -*- coding: utf-8 -*- # ---------------------------从文本中构建词条向量------------------------- # 1 要从文本中获取特征,需要先拆分文本,这里特征是指来自文本的词条,每个词 # 条是字符的任意组合。词条可以理解为单词,当然也可以是非单词词条,比如URL # IP地址或者其他任意字符串 # 将文本拆分成词条向量后,将每一个文本片段表示为一个词条向量,值为1表示出现 # 在文档中,值为0表示词条未出现 # 导入numpy from numpy import * def loadDataSet(): # 词条切分后的文档集合,列表每一行代表一个文档 postingList = [['my', 'dog', 'has', 'flea', \ 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', \ 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['my', 'licks', 'ate', 'my', 'steak', 'how', \ 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']] # 由人工标注的每篇文档的类标签 classVec = [0, 1, 0, 1, 0, 1] return postingList, classVec # 统计所有文档中出现的词条列表 def createVocabList(dataSet): # 新建一个存放词条的集合 vocabSet = set([]) # 遍历文档集合中的每一篇文档 for document in dataSet: # 将文档列表转为集合的形式,保证每个词条的唯一性 # 然后与vocabSet取并集,向vocabSet中添加没有出现 # 的新的词条 vocabSet = vocabSet | set(document) # 再将集合转化为列表,便于接下来的处理 return list(vocabSet) # 根据词条列表中的词条是否在文档中出现(出现1,未出现0),将文档转化为词条向量 def setOfWords2Vec(vocabSet, inputSet): # 新建一个长度为vocabSet的列表,并且各维度元素初始化为0 returnVec = [0] * len(vocabSet) # 遍历文档中的每一个词条 for word in inputSet: # 如果词条在词条列表中出现 if word in vocabSet: # 通过列表获取当前word的索引(下标) # 将词条向量中的对应下标的项由0改为1 returnVec[vocabSet.index(word)] = 1 else: print('the word: %s is not in my vocabulary! ' % 'word') # 返回inputet转化后的词条向量 return returnVec # 训练算法,从词向量计算概率p(w0|ci)...及p(ci) # @trainMatrix:由每篇文档的词条向量组成的文档矩阵 # @trainCategory:每篇文档的类标签组成的向量 def trainNB0(trainMatrix, trainCategory): # 获取文档矩阵中文档的数目 numTrainDocs = len(trainMatrix) # 获取词条向量的长度 numWords = len(trainMatrix[0]) # 所有文档中属于类1所占的比例p(c=1) pAbusive = sum(trainCategory) / float(numTrainDocs) # 创建一个长度为词条向量等长的列表 p0Num = zeros(numWords); p1Num = zeros(numWords) p0Denom = 0.0; p1Denom = 0.0 # 遍历每一篇文档的词条向量 for i in range(numTrainDocs): # 如果该词条向量对应的标签为1 if trainCategory[i] == 1: # 统计所有类别为1的词条向量中各个词条出现的次数 p1Num += trainMatrix[i] # 统计类别为1的词条向量中出现的所有词条的总数 # 即统计类1所有文档中出现单词的数目 p1Denom += sum(trainMatrix[i]) else: # 统计所有类别为0的词条向量中各个词条出现的次数 p0Num += trainMatrix[i] # 统计类别为0的词条向量中出现的所有词条的总数 # 即统计类0所有文档中出现单词的数目 p0Denom += sum(trainMatrix[i]) # 利用NumPy数组计算p(wi|c1) p1Vect = p1Num / p1Denom # 为避免下溢出问题,后面会改为log() # 利用NumPy数组计算p(wi|c0) p0Vect = p0Num / p0Denom # 为避免下溢出问题,后面会改为log() return p0Vect, p1Vect, pAbusive # 朴素贝叶斯分类函数 # @vec2Classify:待测试分类的词条向量 # @p0Vec:类别0所有文档中各个词条出现的频数p(wi|c0) # @p0Vec:类别1所有文档中各个词条出现的频数p(wi|c1) # @pClass1:类别为1的文档占文档总数比例 def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): # 根据朴素贝叶斯分类函数分别计算待分类文档属于类1和类0的概率 p1 = sum(vec2Classify * p1Vec) + log(pClass1) p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1) if p1 > p0: return 1 else: return 0 # 分类测试整体函数 def testingNB(): # 由数据集获取文档矩阵和类标签向量 listOPosts, listClasses = loadDataSet() # 统计所有文档中出现的词条,存入词条列表 myVocabList = createVocabList(listOPosts) # 创建新的列表 trainMat = [] for postinDoc in listOPosts: # 将每篇文档利用words2Vec函数转为词条向量,存入文档矩阵中 trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) \ # 将文档矩阵和类标签向量转为NumPy的数组形式,方便接下来的概率计算 # 调用训练函数,得到相应概率值 p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses)) # 测试文档 testEntry = ['love', 'my', 'dalmation'] # 将测试文档转为词条向量,并转为NumPy数组的形式 thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) # 利用贝叶斯分类函数对测试文档进行分类并打印 print(testEntry, 'classified as:', classifyNB(thisDoc, p0V, p1V, pAb)) # 第二个测试文档 testEntry1 = ['stupid', 'garbage'] # 同样转为词条向量,并转为NumPy数组的形式 thisDoc1 = array(setOfWords2Vec(myVocabList, testEntry1)) print(testEntry1, 'classified as:', classifyNB(thisDoc1, p0V, p1V, pAb)) def bagOfWords2VecMN(vocabList, inputSet): # 词袋向量 returnVec = [0] * len(vocabList) for word in inputSet: if word in vocabList: # 某词每出现一次,次数加1 returnVec[vocabList.index(word)] += 1 return returnVec testingNB()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
可以看到对于简单文档,还是能准确分类的。代码参考https://blog.csdn.net/zhengzhenxian/article/details/79052185,感谢。
(三)支持向量机
SVM(Support Vector Machine,支持向量机)是一类强大的分类器,可以在很多分类问题中给出现有水准很高的分类结果。最简单的 SVM 通过在高维空间中寻找一个最优线性分类面,尽可能地将两类数据分开。对于一特征向量 x 的决策函数为:
f ( x ) = w ⋅ x − b f(x)=w\cdot x-b f(x)=w⋅x−b
其中w 是常规的超平面,b 是偏移量常数。该函数月阈值为 0,它能够很好地将两 类数据分开,使其一类为正数,另一类为负数。通过在训练集上求解那些带有标记
y
i
∈
{
−
1.1
}
y_{i}\in \left \{ -1.1 \right \}
yi∈{−1.1}的特征向量
x
i
x_i
xi的最优化问题,使超平面在两类间具有最大分开间隔,从而找到上面决策函数中的参数w 和 b。该决策函数的常规解是训练集上某些特征向量的线性组合:
w
=
∑
i
a
i
y
i
x
i
w=\sum_{i}^{}a_{i}y_{i}x_{i}
w=i∑aiyixi
所以决策函数可以写为:
f
(
x
)
=
∑
i
a
i
y
i
x
i
⋅
x
−
b
f(x)=\sum_{i}^{}a_{i}y_{i}x_{i}\cdot x-b
f(x)=i∑aiyixi⋅x−b
这里的 i 是从训练集中选出的部分样本,这里选择的样本称为支持向量,因为它们可以帮助定义分类的边界。
支持向量机基本原理:低维不可分转化为高维可分问题。
编写代码
#导入sklearn,用sklearn构造数据集
from sklearn.datasets.samples_generator import make_blobs #数据点生成器
X, y = make_blobs(n_samples=50, centers=2,
random_state=0, cluster_std=0.60)
#画散点图
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
- 1
- 2
- 3
- 4
- 5
- 6
n_samples:样本点个数
centers:簇个数
cluster_std:簇的离散程度,簇的离散程度越大越分散,越小越集中,越好做分类
画几条分割线:
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8

现在有三条线,构建隔离带,越宽越好,画阴影面积,基本思想就是画一条线,找离这条线最近的样本点,但是距离越远越好,感觉说的有点矛盾,但是应该能理解哈,距离是相对其他样本点来说最近,但是实际越远越好。
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10

训练一个基本的SVM
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear')
model.fit(X, y)
- 1
- 2
- 3
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma=‘auto’, kernel=‘linear’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
#绘图函数 def plot_svc_decision_function(model, ax=None, plot_support=True): """Plot the decision function for a 2D SVC""" if ax is None: ax = plt.gca() xlim = ax.get_xlim() ylim = ax.get_ylim() # create grid to evaluate model x = np.linspace(xlim[0], xlim[1], 30) y = np.linspace(ylim[0], ylim[1], 30) Y, X = np.meshgrid(y, x) xy = np.vstack([X.ravel(), Y.ravel()]).T P = model.decision_function(xy).reshape(X.shape) # plot decision boundary and margins ax.contour(X, Y, P, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']) # plot support vectors if plot_support: ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=300, linewidth=1, facecolors='none'); ax.set_xlim(xlim) ax.set_ylim(ylim)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27

1.这条线就是我们希望得到的决策边界
2.观察发现有3个点做了特殊的标记,它们恰好都是边界上的点
3.它们就是我们的support vectors(支持向量)
4.在Scikit-Learn中, 它们存储在这个位置 support_vectors_(一个属性)
#显示每个点的坐标
model.support_vectors_
- 1
- 2
array([[ 0.44359863, 3.11530945],
[ 2.33812285, 3.43116792],
[ 2.06156753, 1.96918596]])
观察可以发现,只需要支持向量我们就可以把模型构建出来。
接下来我们尝试一下,用不同多的数据点,看看效果会不会发生变化。分别使用60个和120个数据点
def plot_svm(N=10, ax=None): X, y = make_blobs(n_samples=200, centers=2, random_state=0, cluster_std=0.60) X = X[:N] y = y[:N] model = SVC(kernel='linear', C=1E10) model.fit(X, y) ax = ax or plt.gca() ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn') ax.set_xlim(-1, 4) ax.set_ylim(-1, 6) plot_svc_decision_function(model, ax) fig, ax = plt.subplots(1, 2, figsize=(16, 6)) fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1) for axi, N in zip(ax, [60, 120]): plot_svm(N, axi) axi.set_title('N = {0}'.format(N))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19

1.左边是60个点的结果,右边的是120个点的结果。
2.观察发现,左右两个图样本密集程度不一样,但是决策边界一模一样(意味着样本多样本少没什么差别,前提是没有引入新的支持向量),只要支持向量没变,其他的数据怎么加无所谓!
SVM 的一个优势是可以使用核函数(kernel function);核函数能够将特征向量映射到 另外一个不同维度的空间中,比如高维度空间。通过核函数映射,依然可以保持对决策函数的控制,从而可以有效地解决非线性或者很难的分类问题。用核函数 K ( x i , x ) K(x_{i} , x) K(xi,x) 替代上面决策函数中的内积 x i ⋅ x x_{i} · x xi⋅x。
下面是一些最常见的核函数:
- 线性是最简单的情况,即在特征空间中的超平面是线性的, K ( x i , x ) = x i ⋅ x K(x_{i} , x)=x_{i} · x K(xi,x)=xi⋅x;
- 多项式用次数为d的多项式对特征进行映射, K ( x i , x ) = ( γ x i ⋅ x + γ ) d , γ > 0 K(x_{i},x)= (\gamma x_{i}\cdot x+\gamma )^{d},\gamma>0 K(xi,x)=(γxi⋅x+γ)d,γ>0
- 经向基函数,通常指数函数是一种极其有效的选择, K ( x i , x ) = e ( − γ ∣ ∣ x i − x ∣ ∣ 2 ) , γ > 0 K(x_{i},x)= e^{\left ( -\gamma ||x_{i}-x||^{2} \right )},\gamma>0 K(xi,x)=e(−γ∣∣xi−x∣∣2),γ>0
- Sigmoid 函数,一个更光滑的超平面替代方案, K ( x i , x ) = t a n h ( γ x i ⋅ x + r ) K(x_{i},x)= tanh(\gamma x_{i}\cdot x+r) K(xi,x)=tanh(γxi⋅x+r)
每个核函数的参数都是在训练阶段确定的。
首先我们先用线性的核来看一下在下面这样比较难的数据集上还能分吗
from sklearn.datasets.samples_generator import make_circles
X, y = make_circles(100, factor=.1, noise=.1)
clf = SVC(kernel='linear').fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf, plot_support=False);
- 1
- 2
- 3
- 4
- 5
- 6
- 7

可以观察到,红色的点和黄色的点串在一起了,使用linear支持向量机,分类效果并不理想。
现在尝试高维核变换
#加入了新的维度r
from mpl_toolkits import mplot3d
r = np.exp(-(X ** 2).sum(1))
def plot_3D(elev=30, azim=30, X=X, y=y):
ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
ax.view_init(elev=elev, azim=azim)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('r')
plot_3D(elev=45, azim=45, X=X, y=y)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12

可以看到分类效果大大改善。
#加入径向基函数
clf = SVC(kernel='rbf', C=1E6)
clf.fit(X, y)
- 1
- 2
- 3
SVC(C=1000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma=‘auto’, kernel=‘rbf’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=300, lw=1, facecolors='none');
- 1
- 2
- 3
- 4

原来线性不可分问题,做了一个非线性变换,就能拟合这个数据。非线性在很多数据集上表达效果更好一些。
调节SVM参数:
调节C参数:
- 当C趋近于无穷大时:意味着分类严格不能有错误
- 当C趋近于很小的时:意味着可以有更大的错误容忍
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');
- 1
- 2
- 3

X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.8)
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, C in zip(ax, [10.0, 0.1]): #C参数
model = SVC(kernel='linear', C=C).fit(X, y)
axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model, axi)
axi.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, lw=1, facecolors='none');
axi.set_title('C = {0:.1f}'.format(C), size=14)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
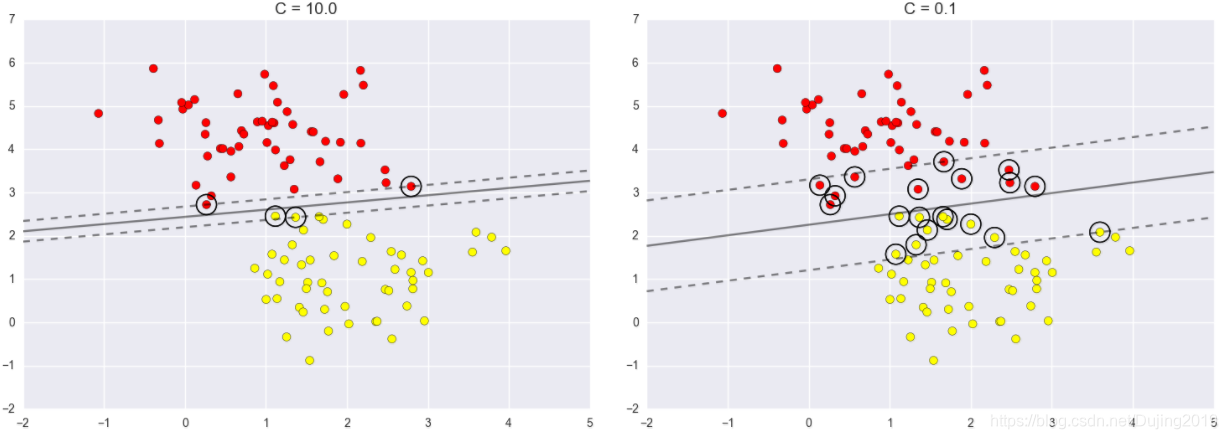
当C大的时候,最明显的缺点,线里面没有进入任何点,但是边界距离非常小,当C小一些的时候,隔离带大了,但是点进来了。所以C并不好评估。
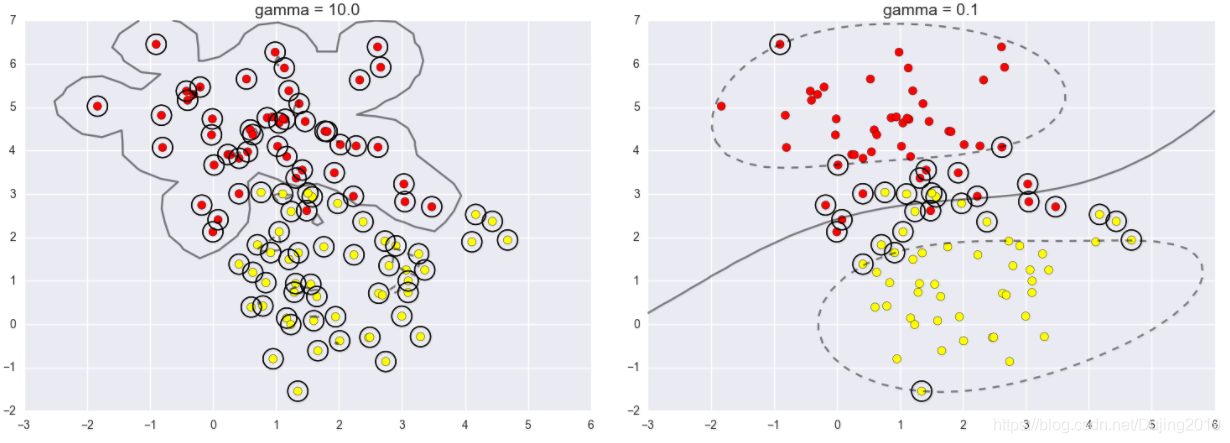
调节gamma参数:
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=1.1)
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, gamma in zip(ax, [10.0, 0.1]):
model = SVC(kernel='rbf', gamma=gamma).fit(X, y)
axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model, axi)
axi.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, lw=1, facecolors='none');
axi.set_title('gamma = {0:.1f}'.format(gamma), size=14)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
gamma控制着模型的复杂程度,越大的值,复杂程度越高,左边gamma值为10,分类效果比较好,但是越复杂的边界,其实实用价值偏低,越小的值;越精简,右边gamma值为0.1,决策边界更平稳,但是分错了很多数据点。
人脸识别问题
使用Wild数据集中的带标签的人脸,该数据集中包含数千张不同公众人物的经过整理的照片。数据集的读取器内置在Scikit-Learn中:
from sklearn.datasets import fetch_lfw_people faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
- 1
- 2
- 3
[‘Ariel Sharon’ ‘Colin Powell’ ‘Donald Rumsfeld’ ‘George W Bush’
‘Gerhard Schroeder’ ‘Hugo Chavez’ ‘Junichiro Koizumi’ ‘Tony Blair’]
(1348, 62, 47)
fig, ax = plt.subplots(3, 5)
for i, axi in enumerate(ax.flat):
axi.imshow(faces.images[i], cmap='bone')
axi.set(xticks=[], yticks=[],
xlabel=faces.target_names[faces.target[i]])
- 1
- 2
- 3
- 4
- 5

每个图的大小是 [62×47],在这里我们就把每一个像素点当成了一个特征,但是这样特征太多了,用PCA降维一下。
from sklearn.svm import SVC
#from sklearn.decomposition import RandomizedPCA
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
pca = PCA(n_components=150, whiten=True, random_state=42) #降维
svc = SVC(kernel='rbf', class_weight='balanced')
model = make_pipeline(pca, svc)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
from sklearn.model_selection import train_test_split
Xtrain, Xtest, ytrain, ytest = train_test_split(faces.data, faces.target,
random_state=40)
- 1
- 2
- 3
使用grid search cross-validation来选择我们的参数
from sklearn.model_selection import GridSearchCV
param_grid = {'svc__C': [1, 5, 10],
'svc__gamma': [0.0001, 0.0005, 0.001]}
grid = GridSearchCV(model, param_grid)
%time grid.fit(Xtrain, ytrain)
print(grid.best_params_)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
得到参数
Wall time: 51.5 s
{‘svc__C’: 5, ‘svc__gamma’: 0.001}
进行分类任务,用模型做预测
model = grid.best_estimator_
yfit = model.predict(Xtest)
yfit.shape
- 1
- 2
- 3
(337,)
fig, ax = plt.subplots(4, 6)
for i, axi in enumerate(ax.flat):
axi.imshow(Xtest[i].reshape(62, 47), cmap='bone')
axi.set(xticks=[], yticks=[])
axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],
color='black' if yfit[i] == ytest[i] else 'red')
fig.suptitle('Predicted Names; Incorrect Labels in Red', size=14);
- 1
- 2
- 3
- 4
- 5
- 6
- 7

预测对了用黑色表示,预测错了用红色表示。
from sklearn.metrics import classification_report
print(classification_report(ytest, yfit,
target_names=faces.target_names))
- 1
- 2
- 3

1.精度(precision) = 正确预测的个数(TP)/被预测正确的个数(TP+FP)
2. 召回率(recall)=正确预测的个数(TP)/预测个数(TP+FN)
3. F1 = 2精度召回率/(精度+召回率)
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest, yfit)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
xticklabels=faces.target_names,
yticklabels=faces.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label');
- 1
- 2
- 3
- 4
- 5
- 6
- 7

混淆矩阵,对角线的意思是测试样本中一个人正确的预测成这个人,非主对角线的意思是一个人被预测成另外一个人,这样显示出来能帮助我们查看哪些人更容易弄混。