数据结构第十四弹---链式二叉树基本操作(下)

1、翻转二叉树

如何翻转一颗二叉树？首先我们可以先观察一下翻转前后的变化。如下图。

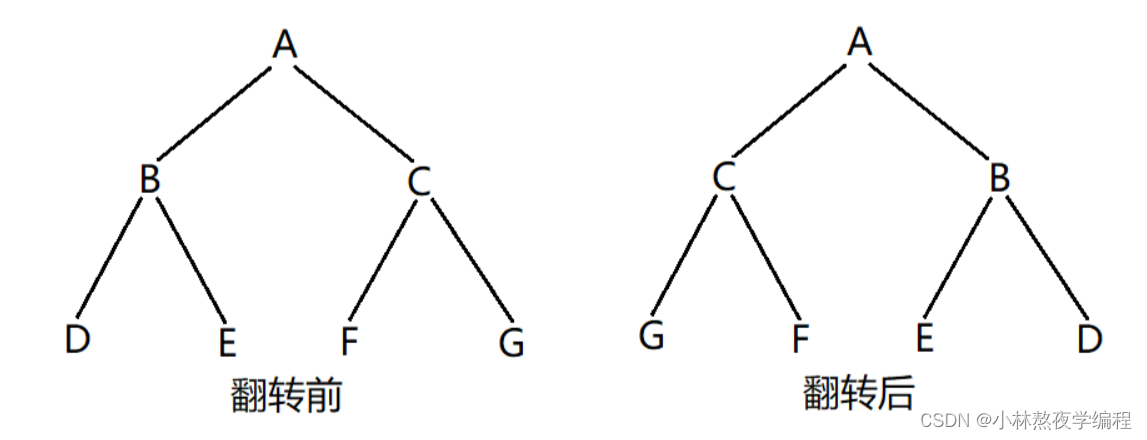
画图分析

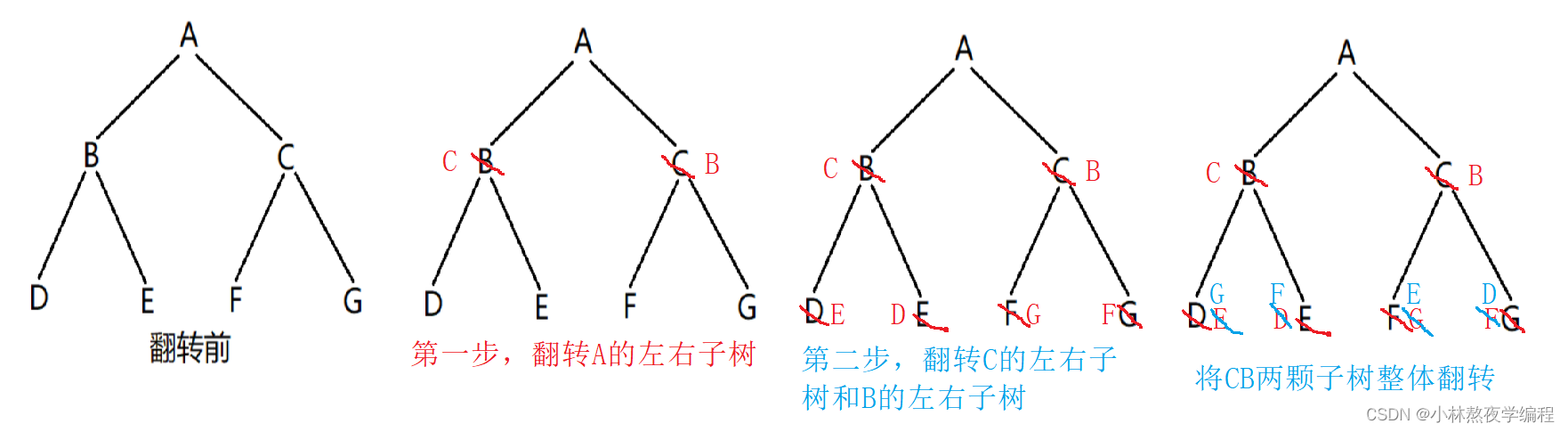
通过观察，可以发现：翻转后，根的左右子树的位置交换了；根的孩子的左右子树的位置也交换了；根的孩子的孩子的左右子树的位置也交换了…

思路：
1、翻转左子树
2、翻转右子树
3、交换左右子树位置

代码实现

//翻转二叉树
BTNode* invertTree(BTNode* root)
{
	if (root == NULL)//根为空，直接返回
		return NULL;
	BTNode* left = invertTree(root->left);//翻转左子树
	BTNode* right = invertTree(root->right);//翻转右子树
	//左右子树位置交换
	root->left = right;
	root->right = left;
	return root;
}
1
2
3
4
5
6
7
8
9
10
11
12

2、判断两棵树是否相同

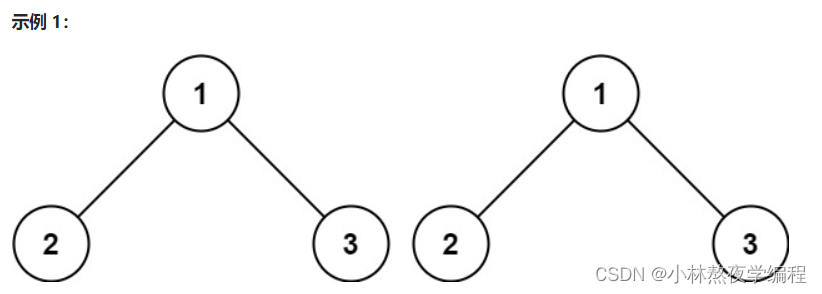
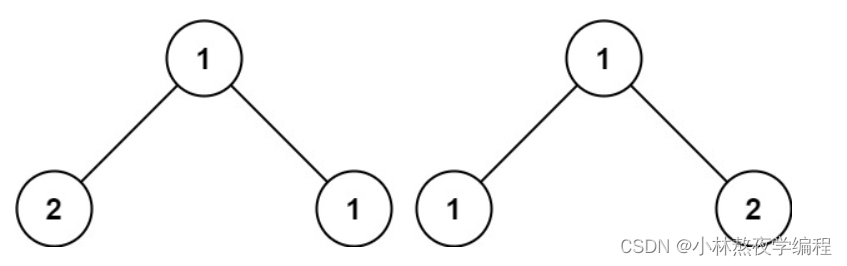
根据上图可知，相等的两棵树需要根节点数值相等，左右子树数值也相等。

因此可以将问题拆分为子问题。
1、两棵树根节点都为空，则相同。
2、两棵树根节点一个为空，则不相同。
3、两棵树根节点都不为空，两棵树的根的值不相等则不相同。
4、判断左右子树是否相等。

代码实现

bool isSameTree(BTNode* p, BTNode* q)
{
	if (p == NULL&&q == NULL)//两棵树均为空，则相同
		return true;
	if (p == NULL || q == NULL)//两棵树中只有一棵树为空，则不相同
		return false;
	if (p->data != q->data)//两棵树根的值不同，则不相同
		return false;
	return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);//两棵树的左子树相同并且右子树相同，则这两棵树相同
}
1
2
3
4
5
6
7
8
9
10

3、判断二叉树是否是单值二叉树

单值二叉树：即二叉树的每个结点具有相同的值。

思路：
1、判断根节点是否为空，为空则是单值二叉树。
2、在左子树存在的情况下，判断左孩子的值是否等于根节点的值。
3、在右子树存在的情况下，判断右孩子的是否等于根节点的值。
4、判断左子树和右子树是否为单值二叉树。

代码实现

//判断二叉树是否是单值二叉树
bool isUnivalTree(BTNode* root)
{
	if (root == NULL)//根为空，是单值二叉树
		return true;
	if (root->left && root->left->data != root->data)//左孩子存在，但左孩子的值不等于根的值
		return false;
	if (root->right && root->right->data != root->data)//右孩子存在，但右孩子的值不等于根的值
		return false;
	return isUnivalTree(root->left) && isUnivalTree(root->right);//左子树是单值二叉树并且右子树是单值二叉树
}

1
2
3
4
5
6
7
8
9
10
11
12

4、对称二叉树

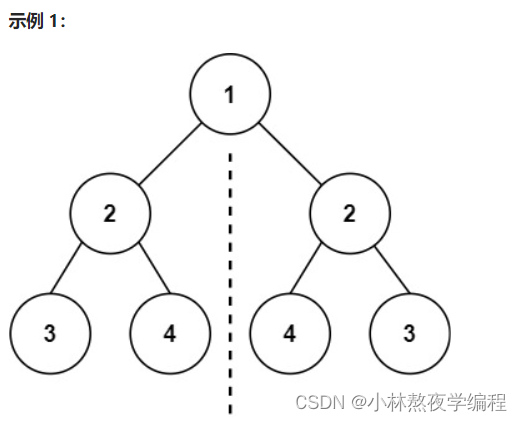
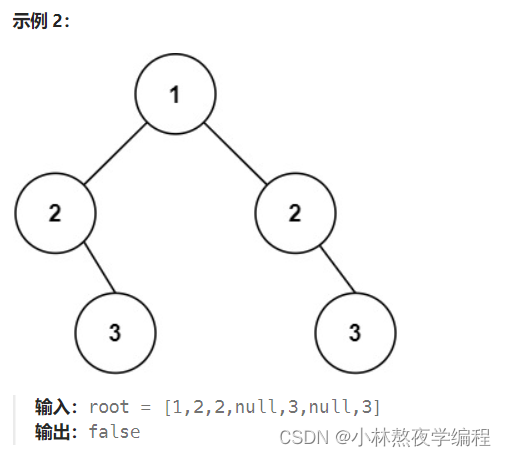
如上图所示，事例一为对称二叉树，事例二不为对称二叉树。可以得知，对称二叉树左孩子等于右孩子，左子树等于右子树。

思路：
1、判断根节点是否为空，为空则为对称二叉树。
2、根节点存在，且左右子树均为空，则为对称二叉树。
3、根节点存在且左右子树其中一个为空，则不为对称二叉树。
4、根节点存在且左右子树均不为空，且左右子树值不相等，则不为对称二叉树。
5、判断左子树是否等于右子树，右子树是否等于左子树。（递归，需要传两个参数，原函数为一个参数，所以创建新的函数实现递归函数）

代码实现

bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2)
{
    //1.都为空的
     if(root1==NULL && root2 == NULL)
          return true;
    //2.其中一个子树为空
    if(root1 == NULL || root2 == NULL)
          return false;
    //3.都不为空
    if(root1->val != root2->val)
           return false;
    return _isSymmetric(root1->left,root2->right)
           && _isSymmetric(root1->right,root2->left);
} 
bool isSymmetric(struct TreeNode* root) 
{
     //根为空，则为真
     if(root==NULL)
     return true;
     //将左子树与右子树进行比较 然后递归 原函数只有一个参数，可以构建一个新函数进行比较
     return _isSymmetric(root->left,root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

5、判断二叉树是否是平衡二叉树

平衡二叉树：即每个结点的左右两个子树的高度差的绝对值不超过1。

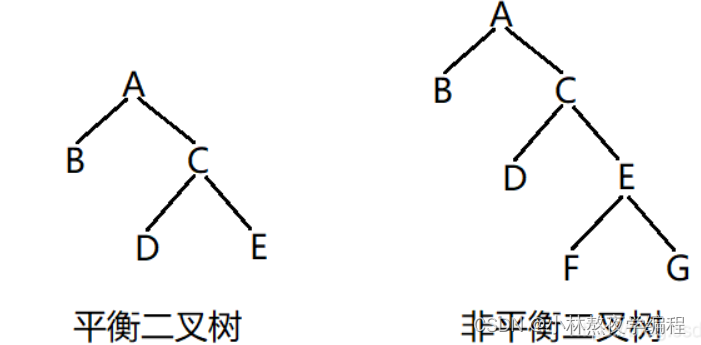
思路：
1、判断根节点是否为空，为空则是平衡二叉树。
2、计算左子树的高度。
3、计算右子树的高度。
4、如果左右子树的高度差不超过1并且左右子树均为平衡二叉树则为平衡二插树。

代码实现

//判断二叉树是否是平衡二叉树
bool isBalanced(BTNode* root)
{
	if (root == NULL)//空树是平衡二叉树
		return true;

	int leftDepth = BinaryTreeMaxDepth(root->left);//求左子树的深度
	int rightDepth = BinaryTreeMaxDepth(root->right);//求右子树的深度
	//左右子树高度差的绝对值不超过1 && 其左子树是平衡二叉树 && 其右子树是平衡二叉树
	return abs(leftDepth - rightDepth) < 2 && isBalanced(root->left) && isBalanced(root->right);
}

1
2
3
4
5
6
7
8
9
10
11
12

6、判断二叉树是否是另一棵二叉树的子树

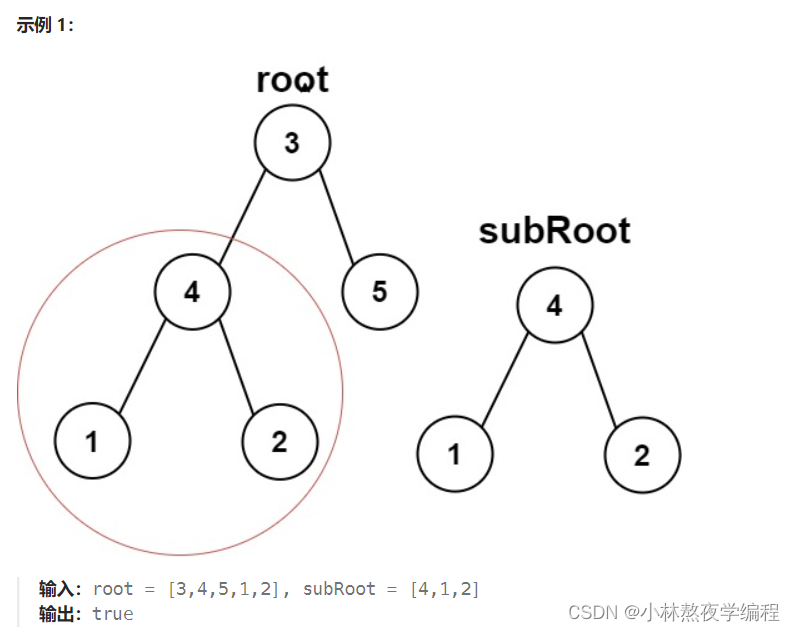
判断二叉树是否是另一个棵树的子树：即root中是否包含与subRoot相同结构和结点值的子树。(subRoot不为空)

思路：
1、如果根节点为空，则不是。
2、判断根节点是否与子树相等，相等则是。
3、判断左子树是否与子树相等，相等则是。
4、判断右子树是否与子树相等，相等则是。

代码实现

bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    //1.都为空
    if(p==NULL && q==NULL)
    return true;
    //2.一个为空
    if(p==NULL || q==NULL)
    return false;
    //3.根都不为空 且val不相等
    if(p->val!=q->val)
    return false;
    //4.根不为空 且根相等 则比较左右子树
    return isSameTree(p->left,q->left) &&
    isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root == NULL)
    return false;
    
    return isSameTree(root,subRoot)//根节点与子树
           ||isSubtree(root->left,subRoot)//左子树与子树
           ||isSubtree(root->right,subRoot);//右子树与子树
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

7、二叉树的销毁

二叉树的销毁跟其他数据结构的销毁基本类似，都是通过遍历销毁。此处需要通过后序遍历进行销毁，因为只有后序遍历销毁左右子树之后还能找到根节点。

代码实现

void TreeDestroy(BTNode* root)
{
	if (root == NULL)
		return;

	TreeDestroy(root->left);//销毁左子树
	TreeDestroy(root->right);//销毁右子树
	free(root);//释放根结点
}

1
2
3
4
5
6
7
8
9
10

8、二叉树的深度遍历

此处的深度遍历跟上一弹的深度遍历不太一样，前面的是通过遍历将数值打印出来，此处是将二叉树的数值通过遍历存储到一个新的数组中。

思路：
1、通过计算二叉树的有效数据个数，确定新开辟的数组的大小。
2、通过遍历将数据存储到数组中。
3、返回数组。

8.1、前序遍历

代码实现

 int RootSize(struct TreeNode* root)
 {
     return root==NULL?0:RootSize(root->left)+RootSize(root->right)+1;
 }
 void PervOrder(struct TreeNode* root,int* a,int* pi)
 {
      if(root==NULL)
      return;
      a[(*pi)++]=root->val;
      PervOrder(root->left,a,pi);
      PervOrder(root->right,a,pi);
 }
int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    //1.计算树的元素个数
    int sz=RootSize(root);
    //2.动态开辟一个树大小的数组
    int* a=(int*)malloc(sizeof(int)*sz);
    //3.前序遍历，将树的值赋值到数组上，但是如果对原函数进行递归遍历，
    //returnSize会多次返回，解决办法是构建新的递归函数
    int i=0;//记录数组下标和大小
    PervOrder(root,a,&i);
    *returnSize=sz;
    return a;//返回数组
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

8.2、中序遍历

代码实现

  int TreeSize(struct TreeNode* root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }
 void InOrder(struct TreeNode* root,int* a,int* pi)
 {
     if(root==NULL)
     return;
     InOrder(root->left,a,pi);
     a[(*pi)++]=root->val;
     InOrder(root->right,a,pi);
 }
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    //计算树的大小
    int sz=TreeSize(root);
    //动态开辟内存
    int* a=(int*)malloc(sizeof(int)*sz);
    //判断是否开辟成功
    if(a==NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    int i=0;
    InOrder(root,a,&i);
    //返回数据个数
    *returnSize=sz;
    //返回数组
    return a;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

8.3、后序遍历

代码实现

 int TreeSize(struct TreeNode* root)
 {
     return root==NULL?0:TreeSize(root->left)+TreeSize(root->right)+1;
 }
 void PostOrder(struct TreeNode* root,int* a,int* pi)
 {
     if(root==NULL)
     return;
     PostOrder(root->left,a,pi);
     PostOrder(root->right,a,pi);
     a[(*pi)++]=root->val;
 }
int* postorderTraversal(struct TreeNode* root, int* returnSize) 
{
    int sz=TreeSize(root);
    int* a=(int*)malloc(sizeof(int)*sz);
    if(a==NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    int i=0;
    PostOrder(root,a,&i);
    *returnSize=sz;
    
    return a;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

9、二叉树的构造和遍历

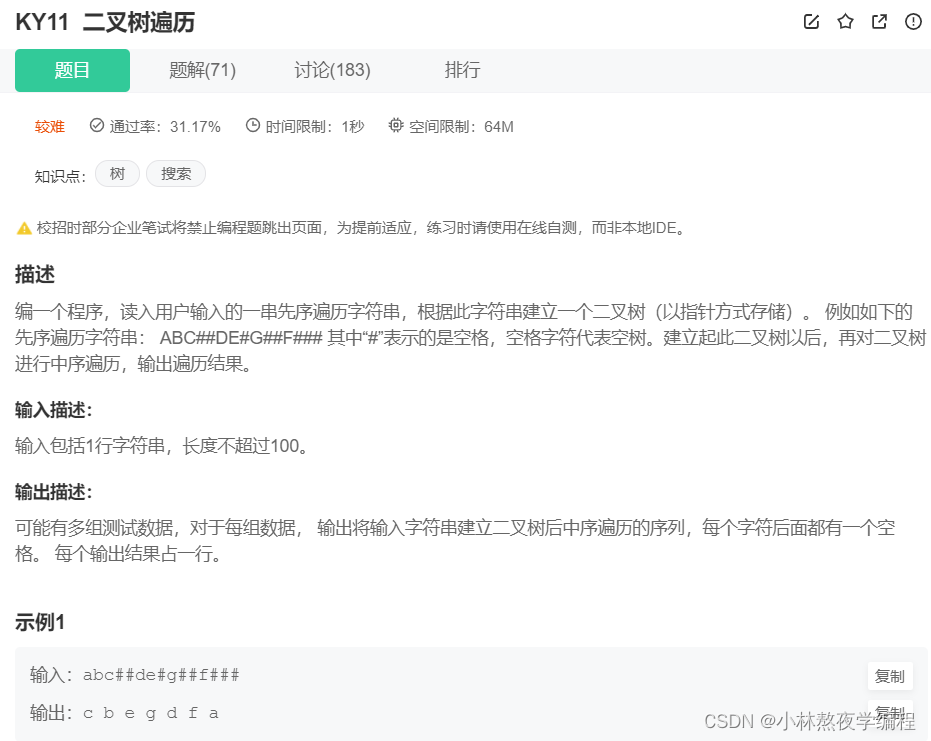
思路：
1、遍历字符串，如果该字符不等于’#’，则按照先序遍历构造二叉树，然后递归构造左右子树。
2、如果字符为’#’，则不再进行构造。
3、构造完之后通过中序遍历打印数据。
代码实现

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char data;
}TreeNode;
//创建树
TreeNode* CreateTree(char* str, int* pi)
{
    if(str[*pi] == '#')//
    {
        (*pi)++;
        return NULL;
    }
    //不是NULL，构建结点
    TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
    root->left = NULL;
    root->right = NULL;
    root->data = str[*pi];
    (*pi)++;
    //递归构建左子树
    root->left = CreateTree(str, pi);
    //递归构建右子树
    root->right = CreateTree(str, pi);
    return root;
}
//中序遍历
void Inorder(TreeNode* root)
{
    if(root == NULL)
        return;
    Inorder(root->left);
    printf("%c ", root->data);
    Inorder(root->right);
}
int main()
{
    char str[100];
    scanf("%s", str);
    int i = 0;
    TreeNode* root = CreateTree(str, &i);
    Inorder(root);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

测试

总结

本篇博客就结束啦，谢谢大家的观看，如果公主少年们有好的建议可以留言喔，谢谢大家啦！