【刷题】备战蓝桥杯 — dfs 算法

送给大家一句话：

风度真美！
即使流泪，也要鼓掌，
即使失望，也要满怀希望。
——刘宝增

1 前言

在蓝桥杯的比赛中，深度优先搜索（DFS，Depth-First Search）算法是一种常用的搜索算法，它通过尽可能深地搜索树的分支，来寻找解决方案。由于其简单和易于实现的特性，DFS成为解决问题的强大工具，尤其是在数据规模较小的情况下。数据在100以内一般使用dfs

运行原理： DFS算法的核心思想是从一个起点开始，沿着树的边走到尽可能深的分支上，然后回溯到之前的分叉点，寻找未探索的分支。这个过程重复进行，直到找到解决方案或探索完所有可能的路径。DFS通常使用递归实现，这使得代码简洁易读。它利用栈（递归调用栈）来记录访问路径，从而实现回溯功能。基本蓝桥杯dfs算法题型可以使用以下模版：

#include <bits/stdc++.h>
//视情况而定
#define int long long 
#define endl '\n'
#define N 1001

using namespace std;
//往往需要一个哈希表来辅助判断
int vis[N] = {0};
void dfs()
{
	//退出条件很重要！！！
	if() return ;
	for()
	{
		//跟新结果
		//继续深入
		dfs();
		//回溯
	}
}

signed main()
{
	//加快读写速度 也可以直接使用C语言标准输入输出函数
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	//多组数据
	int t = 0; cin >> t;
	while(t--)
	{
		//进行基础读入数据
		//构建图 ，记录结构体等
		//解决问题
		dfs();
	}
	return 0；
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

常用于以下题型：

1. 路径问题： 寻找从起点到终点的路径，或者求解所有可能的路径。
2. 排列组合问题： 需要枚举出所有可能的情况时，如全排列、组合选择。
3. 连通性问题： 如判断图中两个节点是否连通，或者求解连通分量。
4. 解谜与回溯问题： 如N 皇后问题、迷宫探索、数独解题等。

注意事项：

• 栈溢出问题（一般不用考虑）： 由于DFS使用递归实现，深度过大时可能会导致栈溢出。针对这一点，可以尝试使用迭代深化搜索（IDS）或非递归方式实现DFS。
• 重复状态处理（一定要仔细）： 在搜索过程中可能会遇到重复状态，如果不加以处理，可能会导致算法陷入无限循环。通常使用访问标记（如访问数组）来避免重复访问。
• 选择合适的剪枝策略（尽力而行）： 合理的剪枝可以显著提高DFS的效率。通过预先判断某些路径是否可能达到目标，从而避免无效搜索。

通过以上的解析，我们可以看到DFS不仅在蓝桥杯中，在很多算法竞赛和实际问题解决中都是一个非常实用的工具。它虽然在处理大数据量时可能会遇到性能瓶颈，但在数据量适中、需要深度搜索解决方案的问题上，DFS仍然是一个十分可靠的选择。
下面我们来一起做几道竞赛题目来试试手！

2 洛谷 P1030 [NOIP2001 普及组] 求先序排列

题目描述

给出一棵二叉树的中序与后序排列。求出它的先序排列。（约定树结点用不同的大写字母表示，且二叉树的节点个数 ≤8）

输入格式
共两行，均为大写字母组成的字符串，表示一棵二叉树的中序与后序排列。
输出格式
共一行一个字符串，表示一棵二叉树的先序。

根据题目，我们需要通过二叉树的中序遍历和后序遍历来写出前序遍历的结果。对于二叉树的确定单凭中序遍历或者后序遍历是不可能的，只有两者结合才能确定一棵完整的二叉树！来看样例：

• 输入
  BADC
  BDCA
• 输出
  ABCD

我们可以画出树的结构：

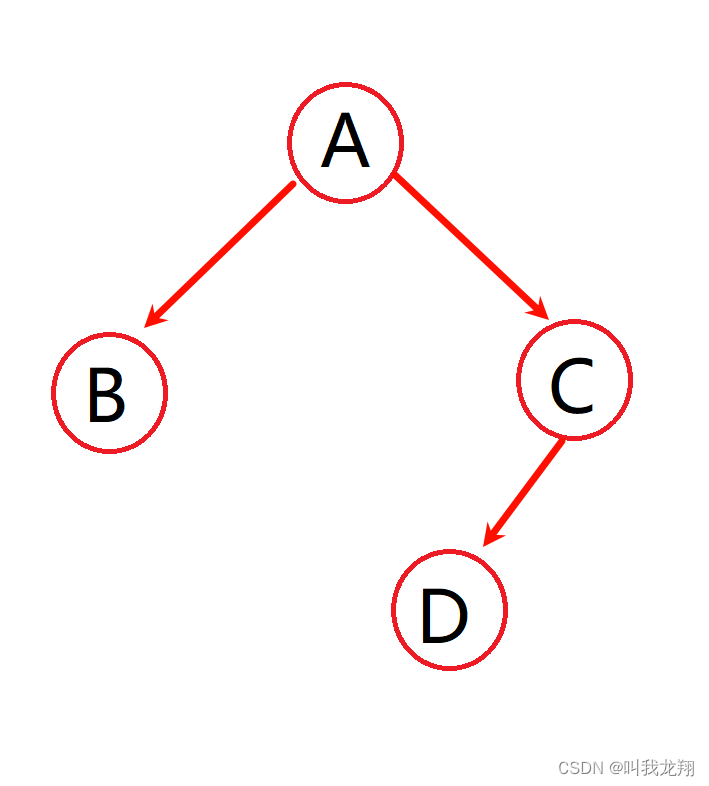
这样前序遍历的结果就有了

算法思路

这道题涉及了二叉树，那么如果不使用dfs 就会非常复杂捏！所以我们把解题交给dfs,重重递归解决问题：

1. 首先通过后序遍历 ， 我们可以确定根节点 （输出打印）
2. 通过在中序遍历中找到根节点的位置，可以区分左右子树
3. 区分出左右子树后，就可以继续寻找左右子树的根节点 ，重复1 - 2操作即可。

#include<iostream>
#include<string>

#define int long long 

using namespace std;

void dfs(string in ,string af)
{
	//为空时直接退出
	if(in.size() <= 0) return ; 
	//通过后序遍历获取根节点 
	char root = af[af.size() - 1];
	//输出
	cout << root;
	//分割左右子树 先变量左子树 再遍历右子树 
	int pos = in.find(root);  
	//注意substr的使用方法 （pos，len）从pos位置开始遍历len个数据
	dfs(in.substr(0 , pos), af.substr(0 , pos));
	dfs(in.substr(pos + 1 , in.size() - 1 - pos), af.substr(pos , af.size() - 1 - pos)) ;
}

signed main()
{
	//加快读写速度 也可以直接使用C语言标准输入输出函数
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	//通过string 来记录遍历的数据 比较方便（速度比较慢 数据量较小时问题不大）
	string in , af;
	cin >> in;
	cin >> af;
	//开始解决
	dfs(in , af);	
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

其中我们使用了string来记录遍历的数据 ,这样使用起来比较方便，但是速度比较慢（数据量较小时问题不大）。
然后通过不断寻找根节点，打印根节点来完成前序遍历。

提交！全部AC！！！

---

3 洛谷 P1294 高手去散步

链接：高手去散步

题目描述

鳌头山上有 n 个观景点，观景点两两之间有游步道共 m 条。高手的那个它，不喜欢太刺激的过程，因此那些没有路的观景点高手是不会选择去的。另外，她也不喜欢去同一个观景点一次以上。而高手想让他们在一起的路程最长（观景时它不会理高手），已知高手的穿梭机可以让他们在任意一个观景点出发，也在任意一个观景点结束。

输入格式
第一行，两个用空格隔开的整数 n 、 m 之后 m 行，为每条游步道的信息：两端观景点编号、长度。
输出格式
一个整数，表示他们最长相伴的路程。

根据题目描述，我们需要在一张地图中寻找最长的行走路线，直接使用暴力dfs是一种非常好的办法。

算法思路

这里需要对地图进行记录，相比直接的图标来记录（一个一个节点的地图）矩阵来记录地图更加方便，这里就是线性代数的美丽世界。通过 n x n的二维数据模拟矩阵，记录从一个节点前往另一个节点的距离，是不是非常方便：

  1 2 3 4                              
1 0 0 0 0 
2 0 0 0 0  
3 0 0 0 0 
4 0 0 0 0       
1
2
3
4
5

这样的一张矩阵既可以记录4个景点之间是否有道路，并储存道路距离。

有了这张表，接下来的思路就简单了

1. 首先先读入地图
2. 让遍历所有的景点（因为出发点可以是任意一个），并进行最长路程计算
3. 进行最长路程计算的过程是
   • 通过选取地图找到还没有去过的景点，并更新距离，直到没有路为止
   • 开始回溯，保证所以路线均被走过

#include<iostream>
#include<cmath>
#include<cstring>

using namespace std;
//n 个景点  m 条路 
int n , m;
//用来判断是否去过 
int hash1[20 + 20] = {0};
//地图矩阵 （+20 为了防止溢出）
int map[20 + 20][20 + 20]; 
//答案
int maxpath = 0; 

void dfs(int i , int dis)
{
	//对每一条路径进行搜索 
	for(int j = 1 ; j <= n ; j++)
	{
		//存在道路 并且 没去过 进行搜索 
		if(map[i][j] && hash1[j] == 0)
		{
			//更新结果 
			hash1[j] = 1;
			//搜索 
			dfs(j , dis + map[i][j]);
			//回溯 这个很重要！！！
			hash1[j] = 0; 
		} 
		//不存在道路和没去过的景点 说明走完了 更新结果 取最大值
		else{
			maxpath = max(maxpath , dis); 
		}
	}
} 

signed main()
{
	//加快读写速度 也可以直接使用C语言标准输入输出函数
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	
	//创建矩阵 
	cin >> n >> m;
	while(m--)
	{
		//两个景点编号 间隔距离 
		int v1 ,v2 , dis;
		cin >> v1 >> v2 >> dis;
		//储存到地图中 
		map[v1][v2] = dis;
		map[v2][v1] = dis;
	}
	
	//对每个位置进行深度优先搜索
	for(int i = 1 ; i <= n ;i++)
	{
		int dis = 0;
		//记录来过 
		hash1[i] = 1;
		//怕什么 搜！ 
		dfs(i , dis) ;
		//回溯 这个很重要！！！
		hash1[i] = 0; 
		//哈希表归零
		memset(hash1 , 0 ,sizeof(hash1));
	}
	cout << maxpath;
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

代码很好理解，就是把所有可能的路线全部遍历一遍,找到最合适的答案！！！

提交：全部AC!!!

4 蓝桥真题 十三届省赛 飞机降落

链接:飞机降落

题目描述

N架飞机准备降落到某个只有一条跑道的机场。其中第架飞机在T时刻到达机场上空，到达时它的剩余油料还可以继续盘旋D个单位时间，即它最早可以于T时刻开始降落，最晚可以于T+D时刻开始降落。降落过程需要L个单位时间。-架飞机降落完毕时，另一架飞机可以立即在同一时刻开始降落，但是不能在前一架飞机完成降落前开始降落。请你判断N架飞机是否可以全部安全降落。

输入格式
输入包含多组数据。第一行包含一个整数T，代表测试数据的组数。对于每组数据，第一行包含一个整数N。以下N行，每行包含三个整数：T，D和L。
输出格式
对于每组数据，输出YES或者NO，代表是否可以全部安全降落。

样例输入

2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20
1
2
3
4
5
6
7
8
9

样例输出

YES
NO
1
2

样例说明
对于第一组数据，可以安排第3架飞机于0时刻开始降落，20时刻完成降落。安排第2 架飞机于 20时刻开始降落，30时刻完成降落。安排第1架飞机于30时刻开始降落，40时刻完成降落。
对于第二组数据，无论如何安排，都会有飞机不能及时降落。

算法思路

这道题通过数据范围，我们应该想到dfs算法，那么应该如何解呢？？？我们需要一个飞机结构体来记录相应信息，一个哈希表来记录飞机状况。然后获取数据， 接下来就要进行深度优先搜索了：

1. 寻找可以降落的飞机（并标记为已经降落），更新时间
2. 再次寻找可以降落的飞机
3. 如果全部降落，那么返回true

这里的更新时间很有说法：

1. 首先每次的dfs都会有一个现在的时间刻
2. 我们需要判断飞机到达的时间刻加上可以盘旋的时间是否大于当前时间刻，如果满足那么就可以进行降落
3. 需要更新的时间 是 开始降落的时间加上降落所需时间
4. 开始降落的时间是dfs目前的时间刻与飞机到达时间的较大值，因为一定要等到上一架飞机降落后并且当前飞机可以降落才能进行。

这样我们就可以写出基本的思路：

#include<bits/stdc++.h>

using namespace std;

#define N 30

//用来判断是否已经降落
int hash1[N] = {0};
struct plane
{
  //T时刻到达 可以盘旋D时间   降落需要L时间
  int T , D , L;
}P[N];

bool flag = false; // 判断是否成功

void dfs(int n , int cnt , int time)
{
  //已经降落的飞机数量等于总数，那么就成功
  if(n == cnt) 
  {
    flag = true;
    return ;
  }
  else
  {
    //遍历所有飞机
    for(int i = 0 ; i < n ;i++)
    {
      //如果该飞机没有降落 并且 满足可以降落的条件
      if(hash1[i] == 0 && P[i].T + P[i].D  >= time)
      {
        hash1[i] = 1; //降落
        //继续深度搜索 更新时间！！！
        dfs(n, cnt + 1 , max(time , P[i].T) + P[i].L );
        hash1[i] = 0; //回溯
      }
    }
  }
}
signed main()
{
  //加快读写速度 也可以直接使用C语言标准输入输出函数
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
  // t 组数据
  int t = 0; cin >> t;
  while(t--)
  {
    int n = 0; cin >> n; 
    int m = n; int i = 0;
    //读入飞机数据
    while(m--)
    {
      cin >> P[i].T >> P[i].D >> P[i].L;
      i++;
    }
    //开始遍历
    dfs(n , 0 , 0);

    if(flag) cout << "YES\n";
    else cout << "NO\n";
    flag = false;
    memset(hash1 , 0 , sizeof(hash1));
  }
  return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

我们提交：通过所以测试点！！！

5 总结

1. dfs算法在数据较小的情况下可以使用。
2. 一定一定要确定好终止条件，避免栈溢出。
3. 相应做好回溯，保证每次的遍历都是不一样的选择，避免少结果。
4. 针对题目进行对应细节处理，有能力的话可以进行剪枝优化！！！

Thanks♪(･ω･)ﾉ谢谢阅读！！！

下一篇文章见！！！