机器人路径规划：基于改进型A*算法的机器人路径规划（提供Python代码）_a*算法多机器人路径规划

一、A*算法介绍

A*算法最早可追溯到1968年，在IEEE Transactions on Systems Science and Cybernetics中的论文A Formal Basis for the Heuristic Determination of Minimum Cost Paths中首次提出。
https://blog.csdn.net/weixin_46204734/article/details/136790525

参考文献：

[1] Hart P E ,MEMBER,IEEE,et al.A Formal Basis for the Heuristic Determination of Minimum Cost Paths[J].IEEE Transactions on Systems Science and Cybernetics, 2007, 4(2):100-107.DOI:10.1109/TSSC.1968.300136.

[2] Hart P E , Nilsson N J , Raphael B .A Formal Basis for the Heuristic Determination of Minimum Cost Paths[J].IEEE Transactions on Systems Science & Cybernetics, 1972, 4(2):28-29.DOI:10.1145/1056777.1056779.

[2]张海涛,程荫杭.基于A*算法的全局路径搜索[J].微计算机信息, 2007(17):3.DOI:10.3969/j.issn.1008-0570.2007.17.095.

二、部分代码

import numpy as np
import matplotlib.pyplot as plt
 
show_animation = False
use_beam_search = False
use_iterative_deepening = False
use_dynamic_weighting = False
use_theta_star = False
use_jump_point = False
 
beam_capacity = 30
max_theta = 5
only_corners = False
max_corner = 5
w, epsilon, upper_bound_depth = 1, 4, 500
 
 
def draw_horizontal_line(start_x, start_y, length, o_x, o_y, o_dict):
    for i in range(start_x, start_x + length):
        for j in range(start_y, start_y + 2):
            o_x.append(i)
            o_y.append(j)
            o_dict[(i, j)] = True
 
 
def draw_vertical_line(start_x, start_y, length, o_x, o_y, o_dict):
    for i in range(start_x, start_x + 2):
        for j in range(start_y, start_y + length):
            o_x.append(i)
            o_y.append(j)
            o_dict[(i, j)] = True
 
 
def in_line_of_sight(obs_grid, x1, y1, x2, y2):
    t = 0
    while t <= 0.5:
        xt = (1 - t) * x1 + t * x2
        yt = (1 - t) * y1 + t * y2
        if obs_grid[(int(xt), int(yt))]:
            return False, None
        xt = (1 - t) * x2 + t * x1
        yt = (1 - t) * y2 + t * y1
        if obs_grid[(int(xt), int(yt))]:
            return False, None
        t += 0.001
    dist = np.linalg.norm(np.array([x1, y1] - np.array([x2, y2])))
    return True, dist

三、部分结果

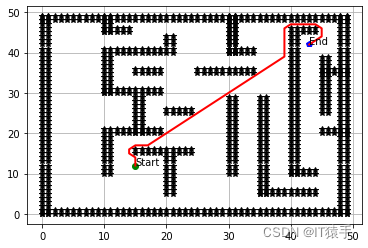
四、完整Python代码

见下方联系方式