- 1微信小程序 实现在底图上绘制扇形_原生微信小程序如何画扇形图表
- 2AlexNet基于MNIST数据集的代码实现_alexnet mnist
- 3Spring Shiro基础组件 SecurityManager_spring securitymanager
- 46月1日，今日信息差
- 5时序违例在FPGA开发流程的分析及解决，结合实际工程_片内时序违例
- 6【Python学习笔记】Python实现文件批量转为utf-8格式_python批量转换utf8
- 7新型Black Matter勒索病毒，勒索300万美金_blackmatter
- 8最新VS code配置C/C++环境(tasks.json, launch.json,c_cpp_properties.json)及运行多个文件、配置Cmake_配置c_cpp_properties.json
- 9vscode使用git_vscode集成git
- 10微服务之SpringCloud AlibabaSeata处理分布式事务
智慧交通项目实战全流程-DeepSort多目标跟踪&车道线检测_人工智能实战项目:智慧交通 行车道检测
赞
踩
1. 项目介绍
2. 算法库
2.1 numba介绍
numba是⼀个⽤于编译Python数组和数值计算函数的编译器，这个编译器能够⼤幅提⾼直接使⽤Python编写的函数的运算速度。
使用方法
numba对代码进⾏加速时，给要优化的函数加上@jit优化器即可。使⽤jit的时候可以让numba来决定什么时候以及怎么做优化。
numba也能够基于输⼊的类型编译⽣成特定的代码，即输入整型，输出会是整型；输入是浮点型，输出也会是浮点型
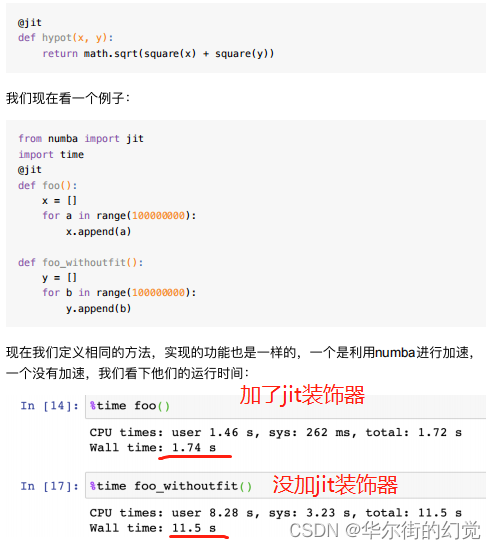
小结：numba装饰器的优点①加速 ②基于输⼊的类型编译⽣成特定的类型
- numba是进⾏python加速的⼯具包
- 在要进⾏加速的python函数中添加装饰器@jit即可实现代码的加速
2.2 imutils介绍
imutils是在OPenCV基础上的⼀个封装，达到更为简结的调⽤OPenCV接⼝的⽬的，它可以轻松的实现图像的平移，旋转，缩放，骨架化等⼀系列的操作。
2.3 cv.dnn
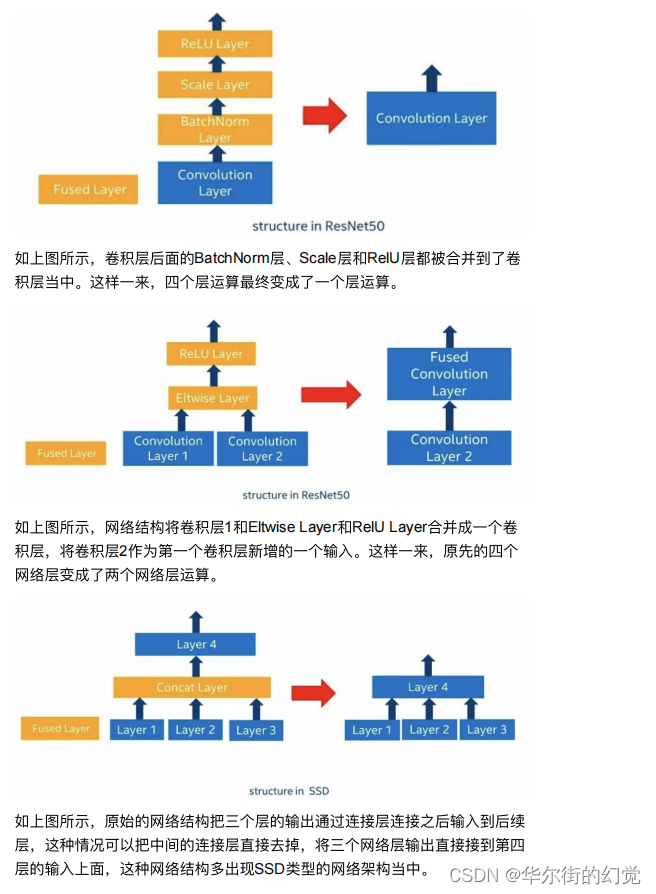
层融合
层融合通过对⽹络结构的分析，把多个层合并到⼀起，从⽽降低⽹络复杂度和减少运算量。
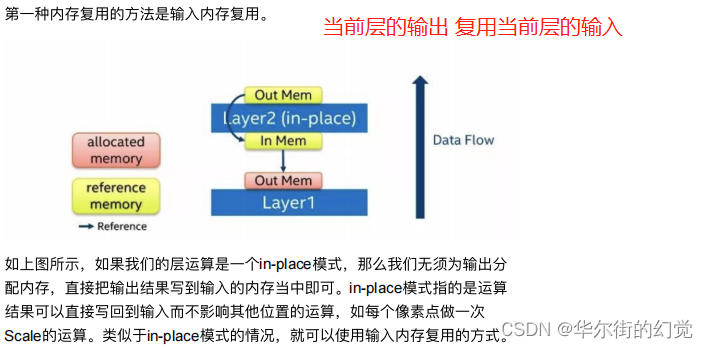
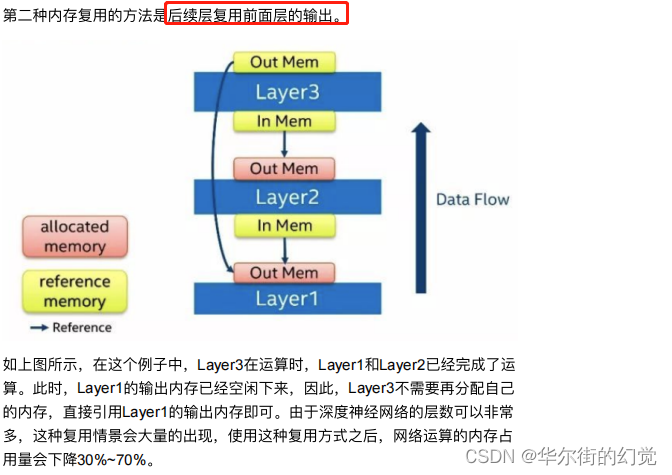
内存复用
2.3.1 dnn.blobFromImage
作⽤：根据输⼊图像，创建维度N（图⽚的个数），通道数C，⾼H和宽W次序的blobs
blobFromImage(image,
scalefactor=None,
size=None,
mean=None,
swapRB=None,
crop=None,
ddepth=None):
- 1
- 2
- 3
- 4
- 5
- 6
- 7
参数：
- image:cv2.imread 读取的图⽚数据 scalefactor: 缩放像素值，如 [0, 255] - [0, 1]
- size:输出blob(图像)的尺⼨，如 (netInWidth, netInHeight)
- mean: 从各通道减均值. 如果输⼊ image 为BGR 次序，且swapRB=True，则 通道次序为 (mean-R, mean-G, mean-B).
- swapRB: 交换 3通道图⽚的第⼀个和最后⼀个通道，如 BGR - RGB
- crop: 图像尺⼨ resize 后是否裁剪. 如果crop=True，则，输⼊图⽚的尺⼨调整 resize后，⼀个边对应与 size 的⼀个维度，⽽另⼀个边的值⼤于等于 size 的 另⼀个维度；然后从resize 后的图⽚中⼼进⾏ crop. 如果 crop=False ，则⽆需 crop，只需保持图⽚的⻓宽⽐
- ddepth: 输出blob 的 Depth. 可选: CV_32F 或 CV_8U
2.3.2 dnn.NMSBoxes
作⽤：根据给定的检测boxes和对应的scores进⾏NMS（⾮极⼤值抑制）处理
原型：
NMSBoxes(bboxes,
scores,
score_threshold,
nms_threshold,
eta=None,
top_k=None)
- 1
- 2
- 3
- 4
- 5
- 6
参数：
- boxes: 待处理的边界框 bounding boxes
- scores: 对于于待处理边界框的 scores
- score_threshold: ⽤于过滤 boxes 的 score 阈值
- nms_threshold: NMS ⽤到的阈值
- indices: NMS 处理后所保留的边界框的索引值 eta: ⾃适应阈值公式中的相关系数：
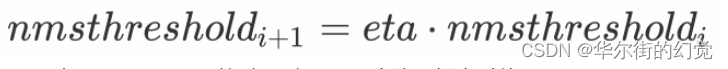
- top_k: 如果 top_k>0，则保留最多 top_k 个边界框索引值.
2.3.2 dnn.readNet
作⽤：加载深度学习⽹络及其模型参数
原型：
readNet(model, config=None, framework=None)
- 1
参数：
- model: 训练的权重参数的模型⼆值⽂件，⽀持的格式有： *.caffemodel (Caffe)、 *.pb (TensorFlow)、 *.t7 或 .net (Torch)、.weights (Darknet)、 *.bin (DLDT).
- config: 包含⽹络配置的⽂本⽂件，⽀持的格式有： *.prototxt(Caffe)、 *.pbtxt (TensorFlow)、 *.cfg (Darknet)、 *.xml (DLDT).
2.3.4 总结
3 车流量检测
学习目标
- 了解多⽬标跟踪的实现⽅法
- 知道⻋流量统计的⽅法
随着城市交通量的迅猛增加，⻋流量统计已成为智能交通系统中⼀项关键技术和热门研究⽅向。⾼效⽽精确的⻋流量检测可以交通管理者和决策者，以及驾驶员提供数据⽀撑，从⽽为交通调度，降低拥堵情况的发⽣，提⾼道路利⽤率有⾮常重要的意义。
⻋流量统计主要有以下⼏种⽅式:
- ⼈⼯统计，需要消耗⼤量的⼈⼒且当⼯作⼈员在⻓时间计数后会因疲惫造成漏检或重复计数，统计结果具有不可验证性。
- 通过安装可接触式或不可接触式的传感器于路⾯进⾏⻋辆计数，可接触式传感
器⼀般铺设于道路下⽅，当⻋辆经过时，传感器内部的电压，磁场或压⼒会发⽣变换弯成⻋辆计数。但这类传感器的安装和维护费⽤很⾼，现在已不再⼤量铺设。不可接触式的包括超声，红外，雷达传感器等，这类容易受到恶劣天⽓的影响使检测精度降低。 - 基于视频的⻋流量统计，也就是本项⽬中实现的⽅法。
该项⽬对输⼊的视频进⾏处理，主要包括以下⼏个步骤：
- 使⽤yoloV3模型进行目标检测，
- 然后使用SORT算法进行目标追踪，使用卡尔曼滤波器进行目标位置预测，并利用匈牙利算法对比目标的相似度，完成车辆目标追踪，
- 利用虚拟线圈的思想实现车辆目标的计数，完成车流量的统计。
项⽬流程如下图所示：
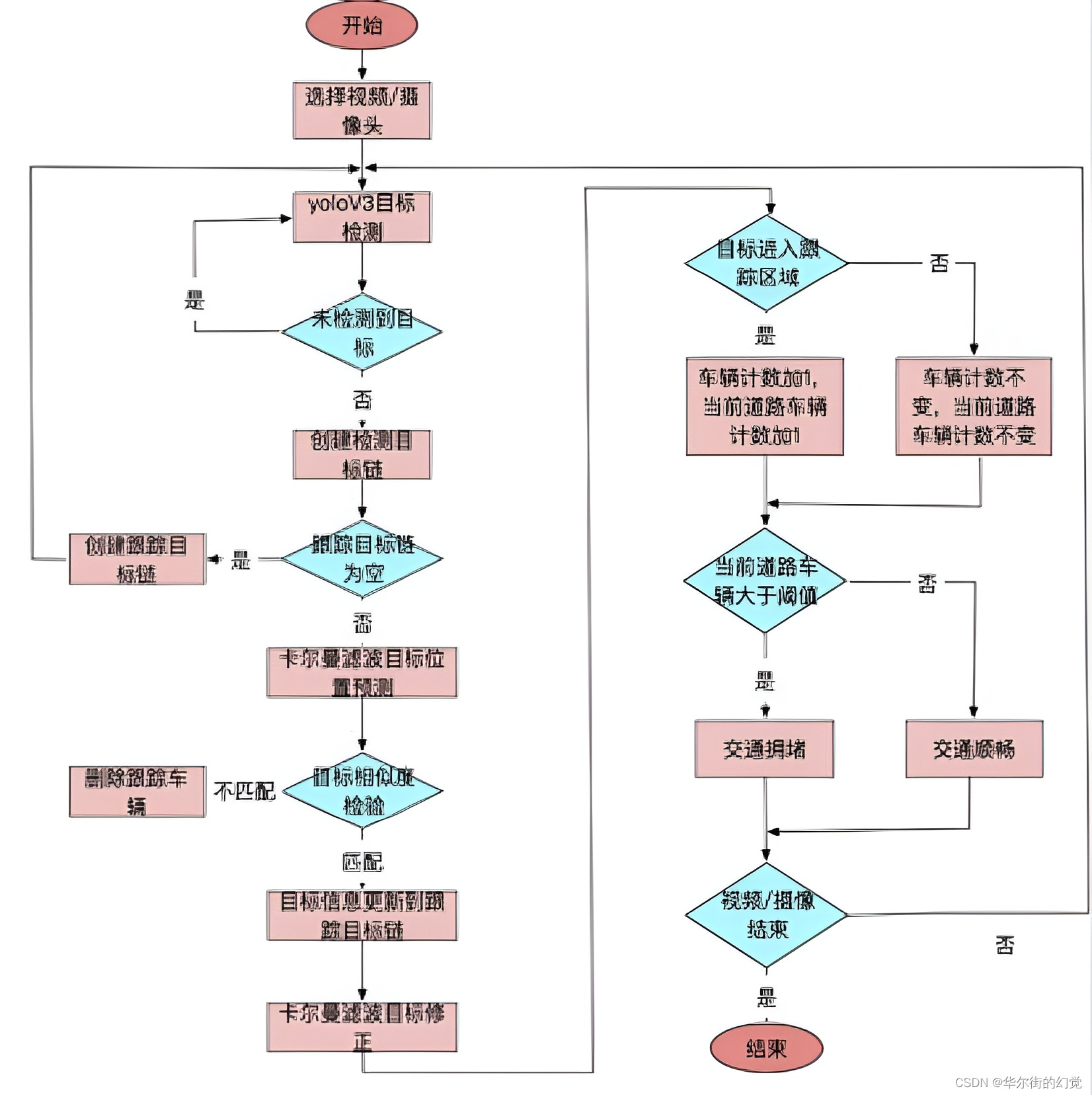
总结
- 目标跟踪方法：使⽤的是sort算法，其中使用卡尔曼滤波器对⽬标位置进⾏估计，利用匈⽛利算法进行目标关联
- 车流量计数：使用虚拟线圈算法对⻋辆进行计数
3.1 多目标跟踪
学习目标：
- 了解多目标跟踪的常见的分类⽅法
- 了解在多目标跟踪中常用的运动模型
- 知道多目标跟踪的常用算法
3.1.1 多目标跟踪分类
多⽬标跟踪，即MOT（Multi-Object Tracking），也就是在⼀段视频中同时跟踪多个目标。MOT主要应⽤在安防监控和自动驾驶等领域中。
多⽬标跟踪可看做多变量估计问题，即给定⼀个图像序列，sti 表示第 t 帧第 i 个目标的状态，St= (st1, st2, …, stM )表示第 t 帧所有⽬标的状态序列，si is:ie= (s , …, s )表示第 i 个⽬标的状态序列，其中is和ie 分别表示⽬标 i 出现的第⼀帧和最后⼀帧，S1:t = (S1 , S2 , …, St )表示所有目标从第⼀帧到第t帧的状态序列。这⾥的状态可以理解为⽬标对应图像中哪个位置，或者是否存在于此图像中，通过匹配得到对应的观测⽬标：O1:t = (O 1, O 2, …, Ot )。
3.1.1.1 初始化方法
多目标跟踪问题中并不是所有目标都会在第⼀帧出现，也并不是所有目标都会出现在每⼀帧。那如何对出现的目标进⾏初始化，可以作为跟踪算法的分类表征。常见的初始化方法分为两⼤类，⼀个是【基于检测的跟踪】Detection-Based-Tracking(DBT)，⼀个是【不基于检测的跟踪】Detection-Free-Tracking(DFT)。下图⽐较形象地说明了两类算法的区别。
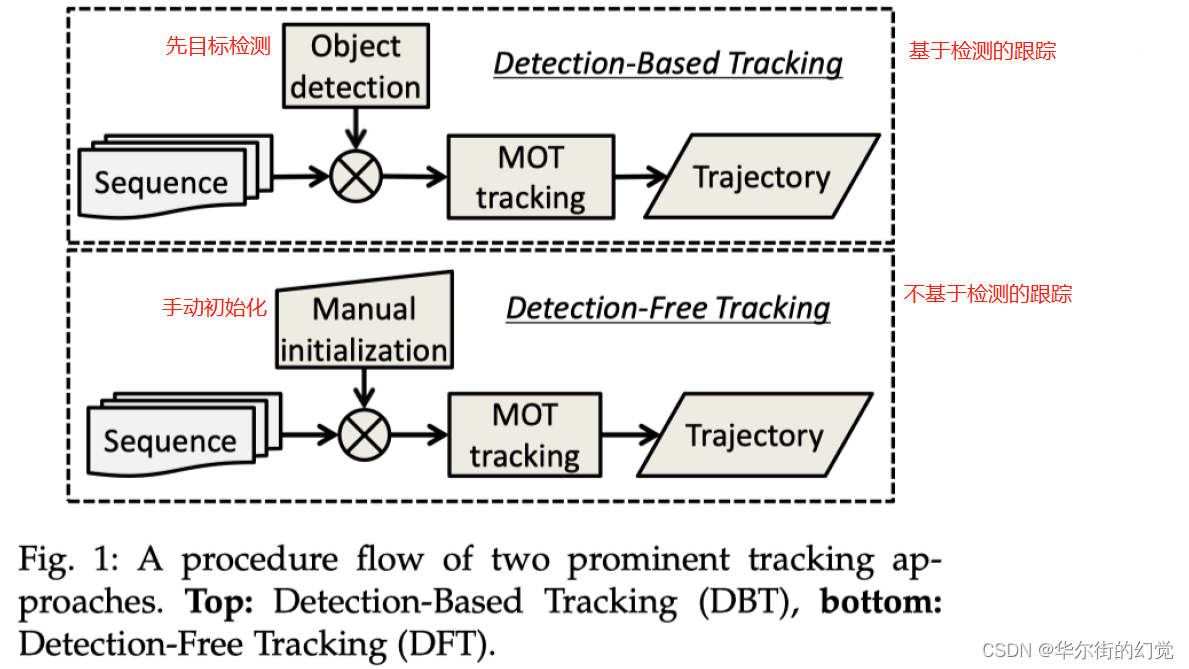
- DBT（常用）
DBT的方式就是典型的tracking-by-detection模式，即先检测目标，然后将目标关联进入跟踪轨迹中。那么就存在两个问题，第一，该跟踪方式非常依赖目标检测器的性能，第二，目标检测的实质是分类和回归，即该跟踪方式只能针对特定的目标类型，如:行人、车辆、动物。DBT则是目前业界研究的主流 - DFT
DFT是单目标跟踪领域的常用初始化方法，即每当新目标出现时，人为告诉算法新目标的位置，这样做的好处是target free，坏处就是过程比较麻烦，存在过多的交互，所以DBT相对来说更受欢迎。
3.1.1.2 处理模式
MOT也存在着不同的处理模式，在线Online 和 离线Ofline两大类，其主要区别在于是否用到了后续帧的信息。下图形象解释了Online与Offine跟踪的区别。
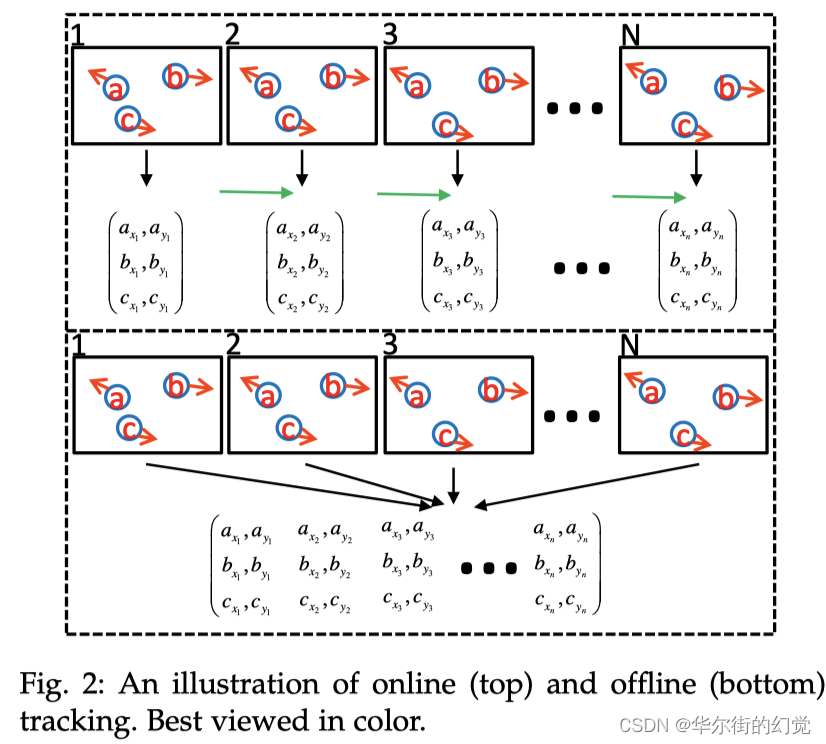
- Online Tracking（常用）
Online Tracking是对视频顿逐顿进行处理，当前帧的跟踪仅利用过去的信息。 - Offline Tracking
不同于Online Tracking，Offline Tracking会利用前后视频帧的信息对当前帧进行目标跟踪，这种方式只适用于视频，如果应用于摄像头，则会有滞后效应,通常采用时间窗方式进行处理，以节省内存和加速。
3.1.2 多目标跟踪的运动模型
为了简化多目标跟踪的难度，我们引入运动模型类简化求解过程，运动模型捕捉目标的动态行为，它估计目标在未来帧中的潜在位置，从而减少搜索空间。在大多数情况下，假设目标在现实中是平缓运动的，那么在图像空间也是如此。对于车辆的运动，大致可分为线性和非线性两种运动:
- 线性运动： 线性运动模型是目前最主流的模型，即假设目标的运动属性平稳(速度，加速度，位置) ;
- 非线性运动：虽然线性运动模型比较常用，但由于存在它解决不了的问题，非线性运动模型随之诞生。它可以使tracklets间运动相似度计算得更加准确
3.1.3 多目标跟踪常用算法
多目标跟踪中基于神经网络的算法，端到端的算法并不多，主要还在实验室的刷榜阶段，模型复杂，速度慢，追踪结果也不好，我们就不再介绍，主要给大家介绍以下两种主流的算法
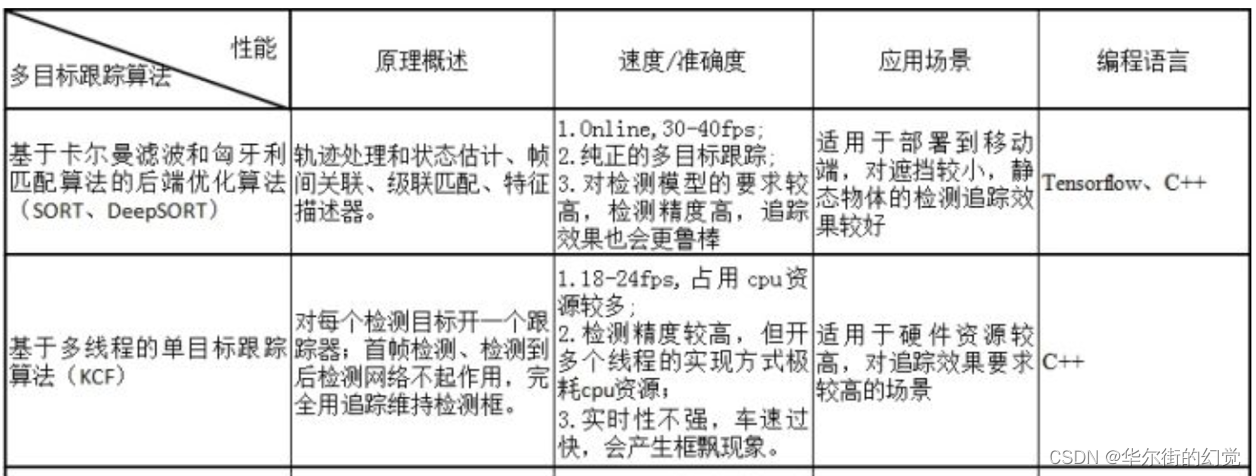
3.1.3.1 基于Kalman和KM算法的后端优化算法
该类算法能达到实时性，但依赖于检测算法效果要好，特征区分要好 (输出最终结果的好坏依赖于较强的检测算法，而基于卡尔曼加匈牙利匹配的追踪算法作用在于能够输出检测目标的id，其次能保证追踪算法的实时性)，这样追踪效果会好，id切换少。代表性的算法是SORT / DeepSORT.
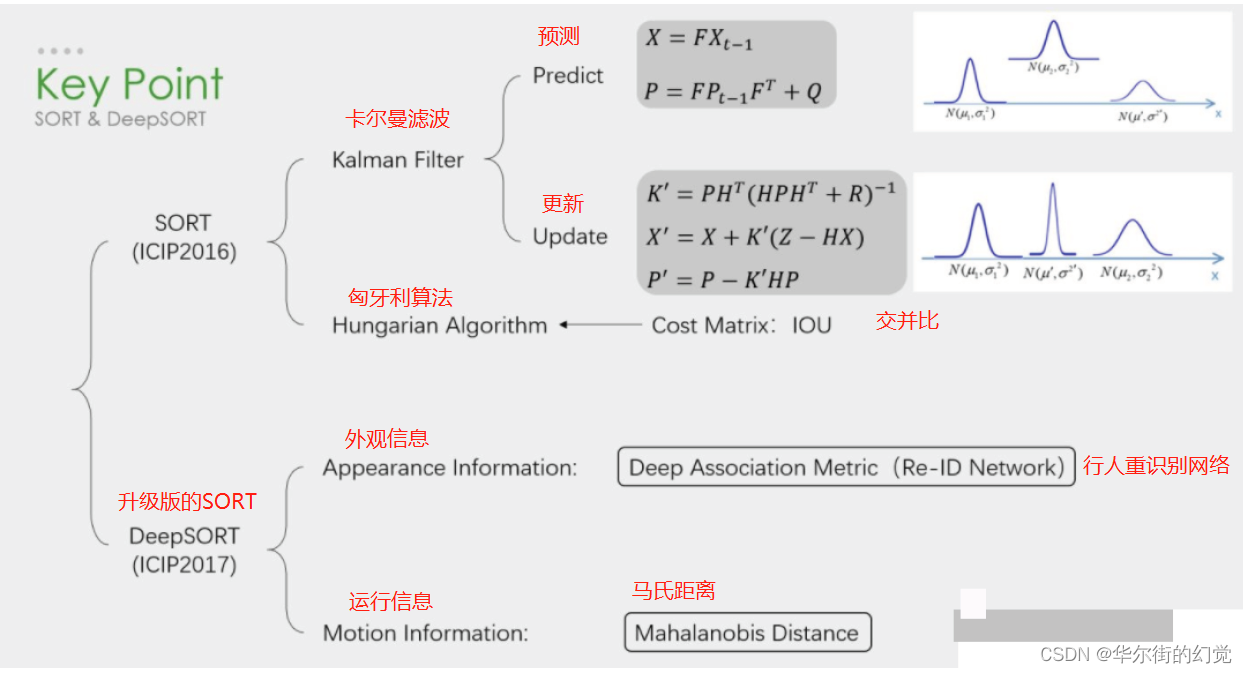
SORT 是一种实用的多目标跟踪算法，引入了线性速度模型与卡尔曼滤波来进行位置预测，在无合适匹配检测框的情况下，使用运动模型来预测物体的位置。匈牙利算法是一种寻找二分图的最大匹配的算法，在多目标跟踪问题中可以简单理解为寻找前后两帧的若干目标的匹配最优解的一种算法。而卡尔曼滤波可以看作是一种运动模型，用来对目标的轨迹进行预测，并且使用确信度较高的跟踪结果进行预测结果的修正。
多目标追踪一般接在目标检测后。在工业界目标检测采用比较多的是yolo检测网络，单阶段式，速度快，精度不差，部署在NV的平台帧率可以达到30fps以上。所以要实现目标检测代码和多目标追踪代码集成的任务，需要先将两者的框架统一：先实现目标检测网络，检测的输出结果主要是将检测框的位置信息输入到多目标追踪算法中。
3.1.3.2 基于多线程的单目标跟踪的多目标跟踪算法
这类算法特点是跟踪效果会很好，因为其为每一类物体都单独分配了一个跟踪器但该算法对目标尺度变化要求较大，参数调试需要合理，同时该算法极耗cpu资源，实时性不高，代表算法是利用KCF进行目标跟踪。
多目标追踪本质上是多个目标同时运动的问题，所以有提出将单目标跟踪器引入到多目标追踪的问题，为每一个目标分配一个KCF跟踪器，然后间接地使用匹配算法来修正那些跟踪失败或新出现的目标。代表性的单目标跟踪算法为核相关滤波算法(KCF)在精度和速度上能够同时达到很高的水平，是当时单目标跟踪最优秀的算法之一，后来的很多单目标跟踪算法都是基于此做的改进。
实际应用过程中会为每个目标分配一个KCF跟踪器并采用多线程的方式来组织这些跟踪器。同时因为实际硬件条件的限制，不可能提供强大的计算力资源，会采用检测器与跟踪器交替进行的跟踪策略。由于检测的帧率不高，使得跟踪的维持效果出现滞后或框飘的现象较为严重，实用性不大。
3.1.4 总结
多目标跟踪，即MOT (Multi-Object Tracking) ，在一段视频中同时跟踪多个目标
- 基于初始化方法
- DBT：基于检测的目标跟踪方法
- DFT：每当新目标出现时，人为告诉算法新目标的位置
- 基于处理模型的方法
- 离线处理：利用前后视频顿的信息对当前帧进行目标跟踪.
- 在线处理：对视频顿逐进行处理，当前帧的跟踪仅利用过去的信息
- 运动模型
- 线性运动(常用)
- 非线性运动
- 常用算法
- 基于Kalman和KM算法的后端优化算法
- 基于多线程的单目标跟踪的多目标跟踪算法
3.2 辅助功能
学习目标
- 能够实现两个目标框的交并比
- 了解候选框在多目标跟踪中的表达方式及相应转换方法
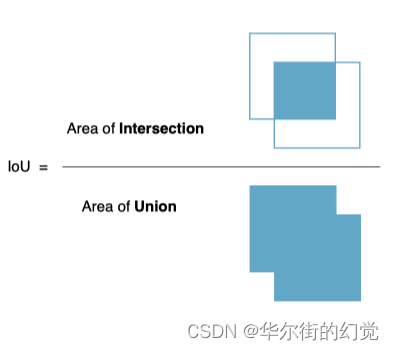
IOU是交并比 (Intersection-over-Union) 是目标检测中使用的一个概念是产生的候选框 (candidate bound) 与原标记框 (ground truth bound) 的交叠率，即它们的交集与并集的比值。最理想情况是完全重叠，即比值为1。在多目标跟踪中，用来判别跟踪框和目标检测框之间的相似度。
3.2.1 交并比
IoU是两个区域的交除以两个区域的并得出的结果。
拿到IOU后，使IOU跟一个阈值做比较，来判断跟踪框（目标）和检测框是否是同一个目标。
def iou(bb_test, bb_gt):
"""
在两个box间计算IOU
:param bb_test: box1 = [x1y1x2y2]
:param bb_gt: box2 = [x1y1x2y2]
:return: 交并⽐IOU
"""
xx1 = np.maximum(bb_test[0], bb_gt[0])
yy1 = np.maximum(bb_test[1], bb_gt[1])
xx2 = np.minimum(bb_test[2], bb_gt[2])
yy2 = np.minimum(bb_test[3], bb_gt[3])
w = np.maximum(0., xx2 - xx1)
h = np.maximum(0., yy2 - yy1)
wh = w * h
o = wh / ((bb_test[2] - bb_test[0]) * (bb_test[3] - bb_test[1]) + (bb_gt[2
bb_gt[3] - bb_gt[1]) - wh)
return o
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
3.2.2 候选框的表示形式
在该项目中候选框有两种表示形式
- [x1,y1,x2,y2] 表示左上角坐标和右下角坐标，目标检测的结果以该方式表示
- [x,y,s,r] 表示中心点坐标，s 是面积尺度，r是纵横比，卡尔曼滤波器中进行运动估计是使用该方式。
这两种方式要进行相互的转换：将候选框从坐标形式转换为中心点坐标和面积的形式
# 将左上角/右下角坐标[x1,y1,x2,y2]转换成中心点坐标[x,y,s,r]
def convert_bbox_to_z(bbox):
"""
将[x1,y1,x2,y2]形式的检测框转为滤波器的状态表示形式[x,y,s,r]。其中x，y是框的中⼼坐标，
:param bbox: [x1,y1,x2,y2] 分别是左上⻆坐标和右下⻆坐标
:return: [ x, y, s, r ] 4⾏1列，其中x,y是box中⼼位置的坐标，s是⾯积，r是纵横⽐w/h
"""
w = bbox[2] - bbox[0] # 宽
h = bbox[3] - bbox[1] # 高
x = bbox[0] + w/2. # 中心点坐标x
y = bbox[1] + w/2. # 中心点坐标y
s = w*h # 面积
r = w/float(h) # 宽高比
return np.array([x,y,s,r]).reshape(4,1) # 4行格式
# 将[x,y,s,r]转换成[x1,y1,x2,y2]
def convert_x_to_bbox(x,score=None):
"""
将[cx，cy，s，r]的⽬标框表示转为[x_min，y_min，x_max，y_max]的形式
:param x:[ x, y, s, r ],其中x,y是box中⼼位置的坐标，s是⾯积，r
:param score: 置信度
:return:[x1,y1,x2,y2],左上⻆坐标和右下⻆坐标
"""
w = np.sqrt(x[2] * x[3]) # 宽：x[2]是s是面积(w*h),x[3]是r是宽高比(w/h),二者相乘即w²,所以开方即得w
h = x[2]/w # 高
x1 = x[0] - w/2 # 左上角x
y1 = x[1] - h/2 # 左上角y
x2 = x[0] + w/2 # 右下角x
y2 = x[1] + h/2 # 右下角y
if score is None: # 若置信度为空
return np.array([x1,y1,x2,y2]).reshape(1,4)
else:
return np.array([x1,y1,x2,y2,score]).reshape(1,5)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
3.2.3 总结
- IOU的计算方法：两个区域的交 比上 两个区域的并，即为IOU
- 候选框不同表示方式之间的转换：
- [x1,y1,x2,y2] 表示左上角坐标和右下角坐标
- [x,y,s,]表示中心点坐标，s 是面积尺度，r是纵横比
3.3 卡尔曼滤波器
学习目标
- 了解filterrpy工具包
- 了解卡尔曼滤波在目标跟踪中的应用
- 知道卡尔曼滤波的原理: 预测阶段和更新阶段
3.3.1 filterrpy
FilterPy是一个实现了各种滤波器的Python模块，它实现著名的卡尔曼滤波和粒子滤波器。我们可以直接调用该库完成卡尔曼滤波器实现。其中的主要模块包括:
- filterpy.kalman
该模块主要实现了各种卡尔曼滤波器，包括常见的线性卡尔曼滤波器，扩展卡尔曼滤波器等 - filterpy.common
该模块主要提供支持实现滤波的各种辅助函数，其中计算噪声矩阵的函数，线性方程离散化的函数等 - filterpy.stats
该模块提供与滤波相关的统计函数，包括多元高斯算法，对数似然算法，PDF及协方差等 - filterpy.monte_carlo
该模块提供了马尔科夫链蒙特卡洛算法，主要用于粒子滤波
开源代码在:
https://github.com/rlabbe/filterpy/tree/master/filterpy/kalman
我们介绍下卡尔曼滤波器的实现，主要分为 预测和更新 两个阶段，在进行滤波之前，需要先进行初始化：
3.3.2 背景介绍
卡尔曼滤波 (Kalman)无论是在单目标还是多目标领域都是很常用的一种算法我们将卡尔曼滤波看做一种运动模型，用来对目标的位置进行预测，并且利用预测结果对跟踪的目标进行修正，属于自动控制理论中的一种方法。
在对视频中的目标进行跟踪时，当目标运动速度较慢时，很容易将前后两帧的目标进行关联，如下图所示：
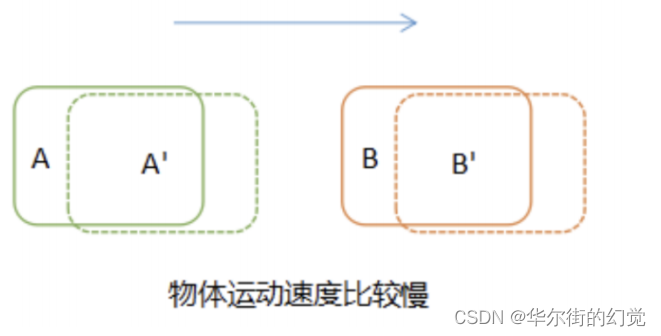
如果目标运动速度比较快，或者进行隔帧检测时，在后续帧中，目标A已运动到前一帧B所在的位置，这时再进行关联就会得到错误的结果，将A与B关联在一起。
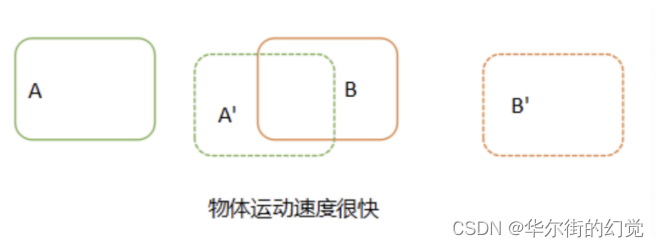
那怎么才能避免这种出现关联误差呢?我们可以在进行目标关联之前，对目标在后续帧中出现的位置进行预测，然后与预测结果进行对比关联，如下图所示：
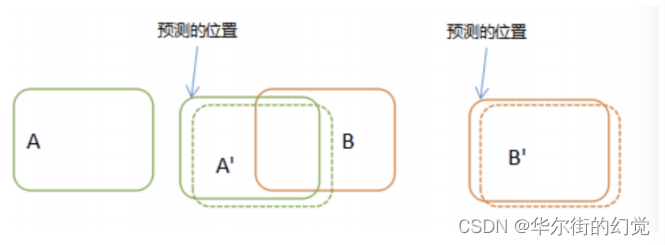
我们在对比关联之前，先预测出A和B在下一顿中的位置，然后再使用实际的检测位置与预测的位置进行对比关联，只要预测足够精确，几乎不会出现由于速度太快而存在的误差。
卡尔曼滤波就可以用来预测目标在后续帧中出现的位置，如下图所示，卡尔曼滤波器就可以根据前面五帧数据目标的位置，预测第6帧目标的位置。
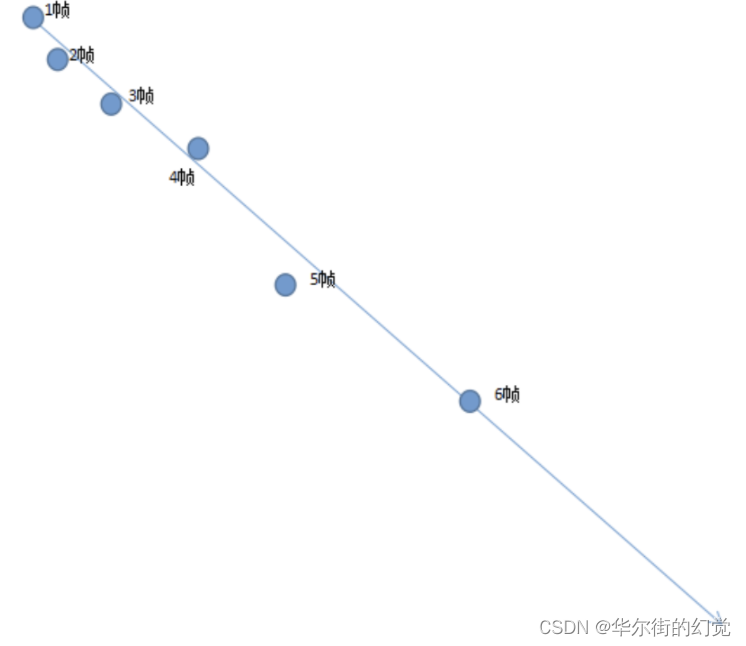
卡尔曼滤波器最大的优点是采用递归的方法来解决线性滤波的问题，它只需要当前的测量值 和 前一个周期的预测值就能够进行状态估计。由于这种递归方法不需要大量的存储空间，每一步的计算量小，计算步骤清晰，非常适合计算机处理，因此卡尔曼滤波受到了普遍的欢迎，在各种领域具有广泛的应用前景。
3.3.3 原理介绍
我们假设一个简单的场景，有一辆小车在行驶，它的速度是v，可以通过观测得到它的位置p,也就是说我们可以实时的观测小车的状态。
-
场景描述
小车在某一时刻的状态表示为一个向量
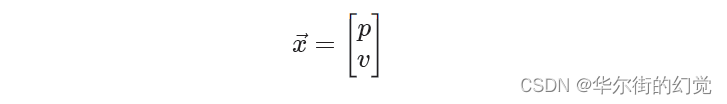
虽然我们比较确定小车此时的状态，无论是计算还是检测都会存在一定的误差，所以我们只能认为当前状态是其真实状态的一个最优估计。那么我们不妨认为当前状态服从一个高斯分布，如下图所示
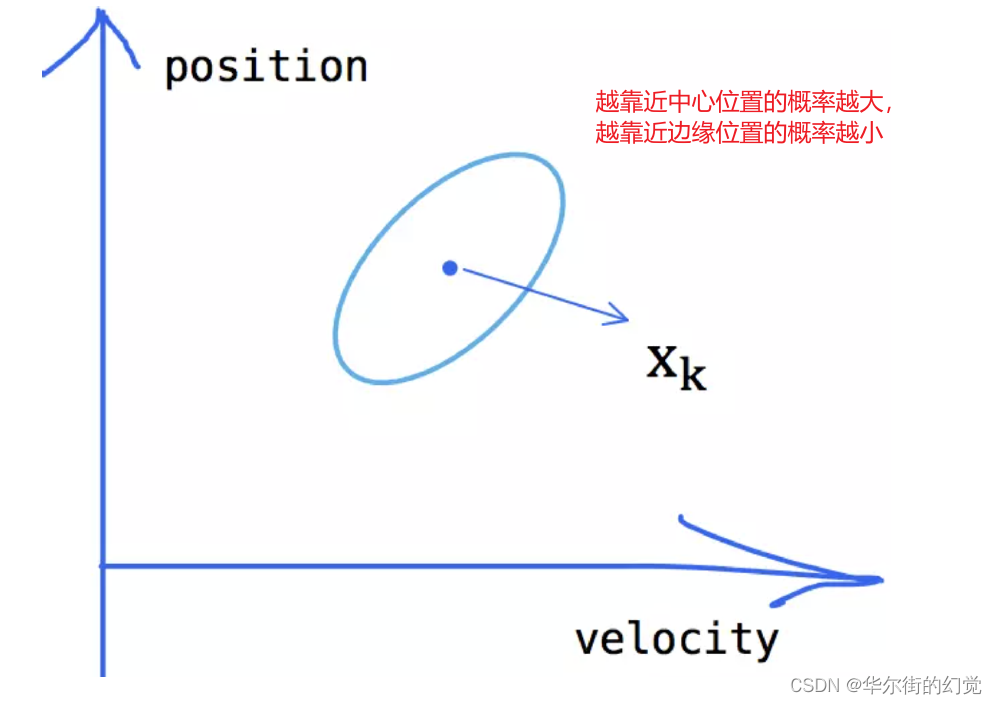
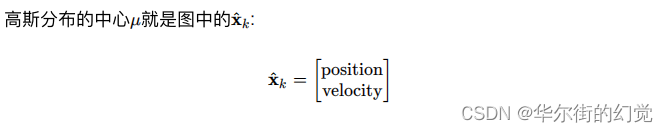
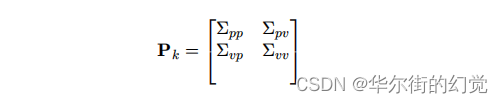
因为我们有两个变量，所以可以⽤⼀个协⽅差矩阵Pk来表示数据之间的相关性和离散程度：- pp - 位置的离散程度
- vv - 速度的离散程度
- pv/vp - 速度和位置的相关性
-
预测下⼀时刻的状态
下面我们需要通过小车的当前状态，运用一些物理学的知识来预测它的下一个状态，即通过k-1时刻的位置和速度，可以推测下一个时刻的状态为：
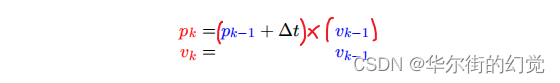
写成矩阵形式就是：
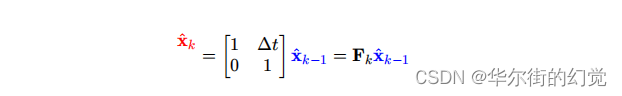
此处的Fk 就是状态转移矩阵。
系统的不确定性和相关性 可以 通过协方差矩阵描述，那根据当前协方差矩阵预测下一时刻的协方差矩阵：
在这⾥我们⽤到了协⽅差的性质：
如果x的协方差矩阵是Σ，那x乘一个矩阵A 的协方差矩阵，就是AΣAT
-
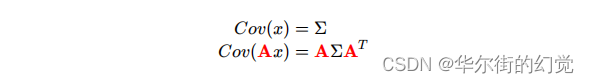
增加系统的内部控制
我们需要对小车进行控制，比如加速和减速，假设某个时刻我们施加的加速度是a，那么下一时刻的位置和速度则应该为：
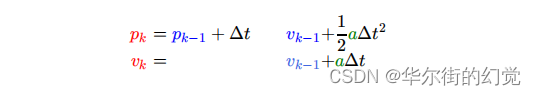
其中，Bk我们称为状态控制矩阵，而Uk称为状态控制向量，含义很明显，前者表明的是加速减速如何改变小车的状态，而后者则表明控制的力度大小和方向
-
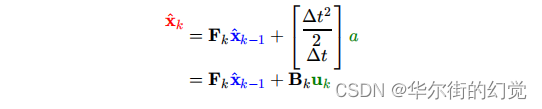
考虑系统的外部影响
外界有很多影响因素能够对小车的状态产生影响，比如说风速等，在这里我们假设外部的不确定因素对小车造成的系统状态误差wk服从高斯分布wk~ N(0, Qk)，至此我们就能得到Kalman滤波中完整的状态预测方程：
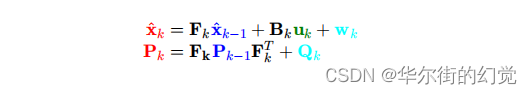一般情况下，我们假设wk为0即可，如果明确均值不为0，就不能省略了，要看实际的应用场景。 -
对观测数据的预测
前面我们通过小车的上一个状态，对它的当前状态做了预测，此时我们要考虑对于小车的状态能够观测到什么呢?小车的当前状态和观测到的数据应该具备某种特定的关系，假设这个关系通过矩阵表示为Hk，如下图所示
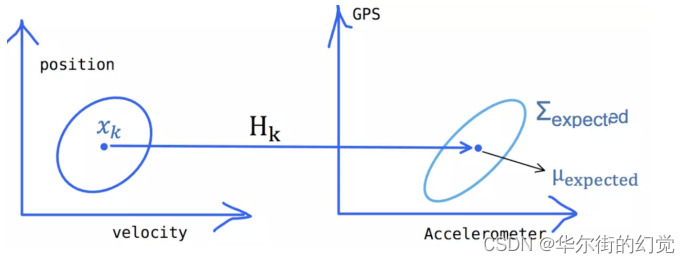
在此前对小车所做的预测状态下，我们的观测值为
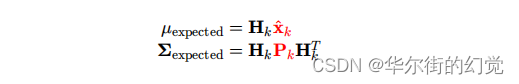
那我们就完成了对观测值的预测：
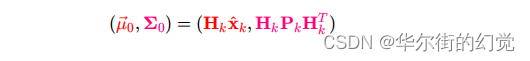
- 实际的观测结果
前⾯推测小车当前的状态，推测了我们的观测数据，但是现实和理想之间必然是存在差距的，我们预测的观测结果和实际的观测结果可能如下图所示：
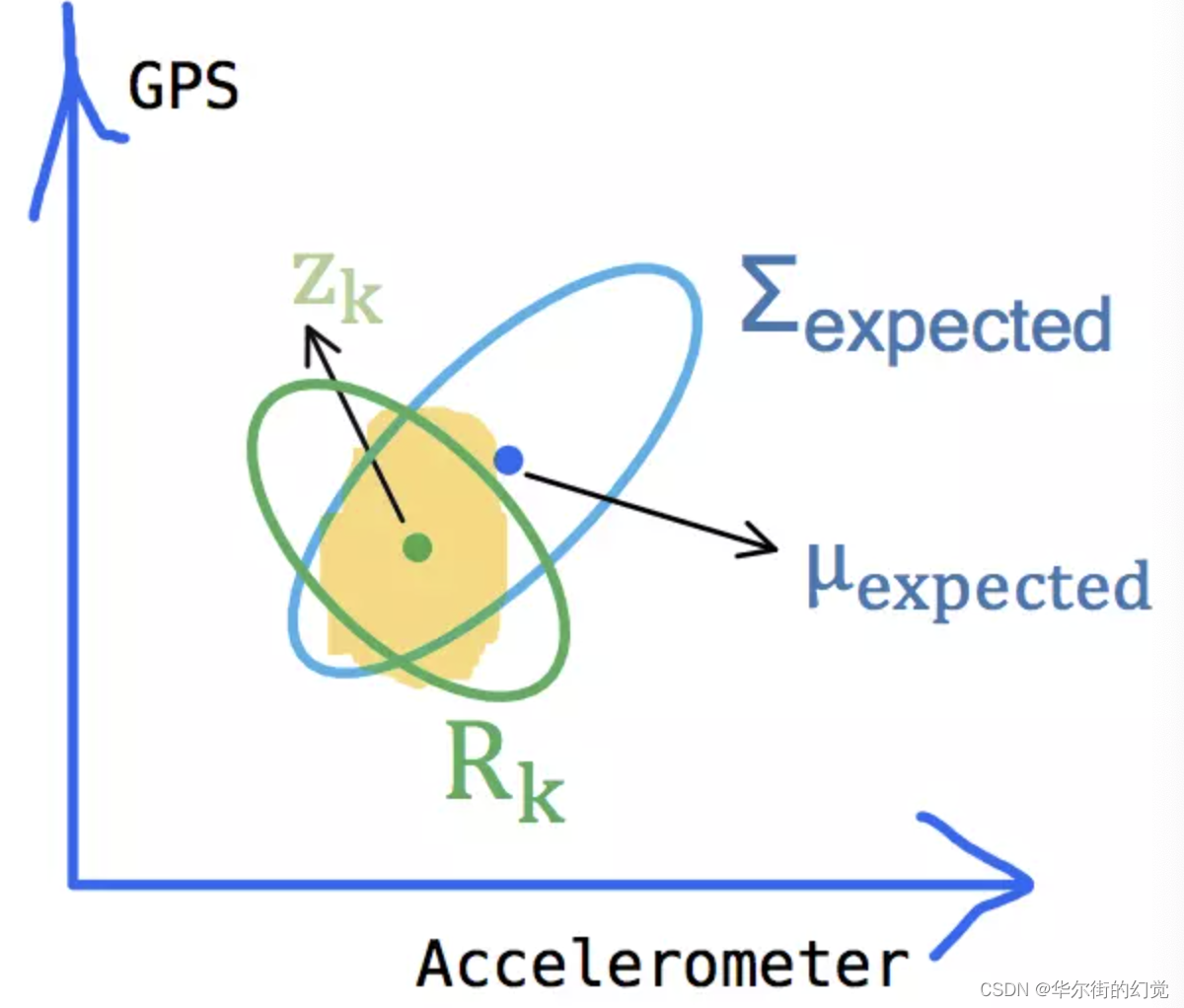
上图中的zk表示实际观测的结果，但是观测的结果肯定也是不准确的，所以我们认为其观测噪声vk是一个均值为0，协方差矩阵为Rk的高斯分布，即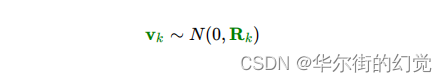
其实也就是说我们对小车的观测值服从高斯分布，Eva真实的情况应该存在以zk为椭圆心的椭圆内，即观测结果服从高斯分布:
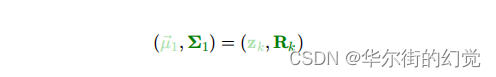
卡尔曼滤波需要做的最重要的最核心的事就是融合预测和观测的结果，充分利用两者的不确定性来得到更加准确的估计。通俗来说就是怎么从上面的两个椭圆中来得到中间淡黄色部分的高斯分布，看起来这是预测和观测高斯分布的重合部分，也就是概率比较高的部分。
- 高斯分布的乘积
对于任意两个高斯分布，将二者相乘之后还是高斯分布，我们利用高斯分布的两个特性进行求解，其一是均值处分布函数取极大值，其二是均值处分布曲线的曲率为其二阶导数，我们可以求出:
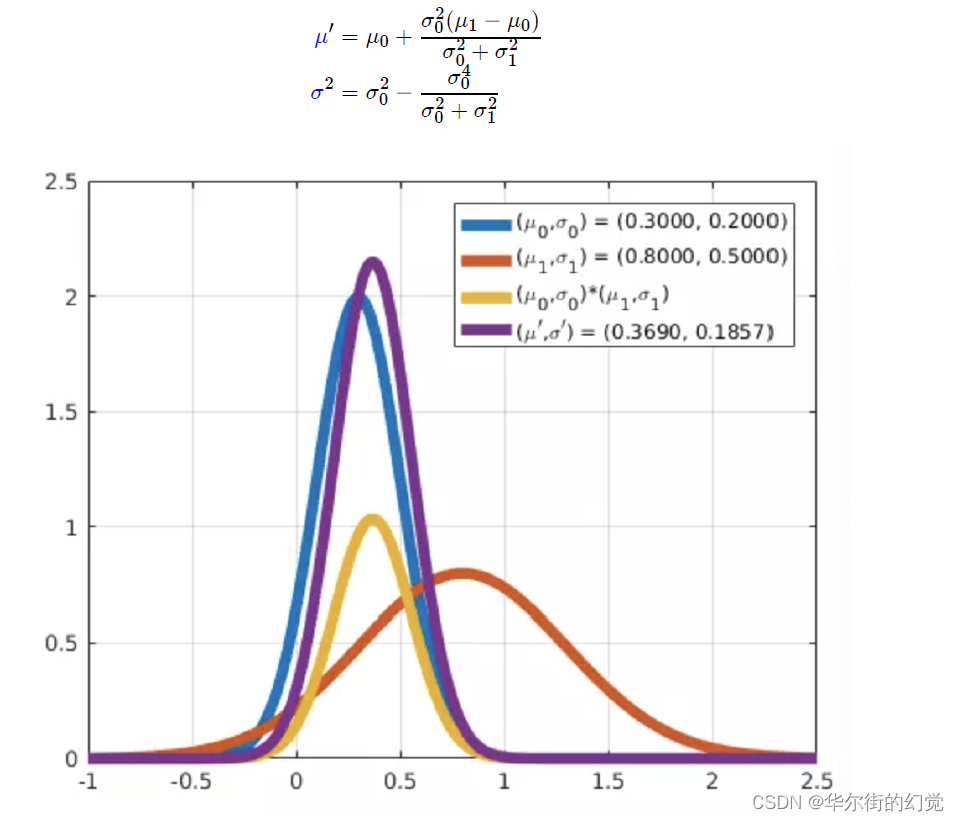
图中蓝色和橙色两个波形的直接乘积是黄色这个波形，紫色是计算了均值和方差的结果，黄色的分布可以通过紫色的波形乘上一个系数得到。
对于高阶的高斯分布
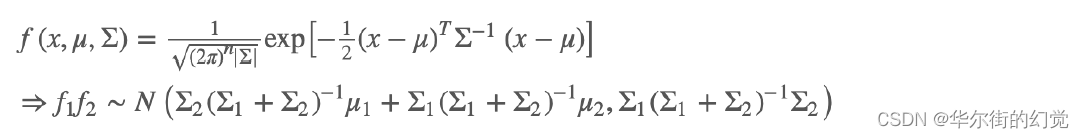
- 新的高斯分布
通过预测和观测值的⾼斯分布的乘积得到的即是卡尔曼滤波的最优估计：
在新的均值和⽅差计算公式中，我们令：
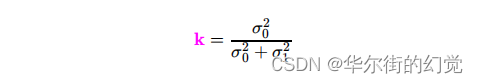
那么可以得到：
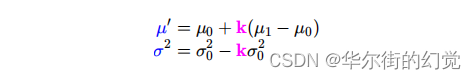
将它们写成矩阵形式就是：
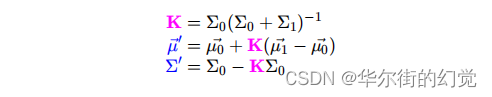
前⾯我们已经得到了预测结果和观测结果服从的两个⾼斯分布，如下：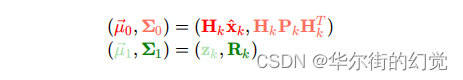
所以我们可以进⾏如下推导，来得到卡尔曼滤波对当前状态(基于预测和观测的)最优估计的计算⽅程：
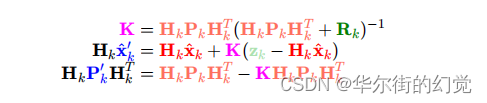
好的，两边化简下，注意 K 可以展开，于是可以得到：
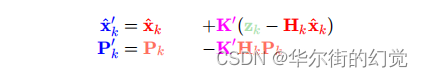
此处的K’就是卡尔曼增益：
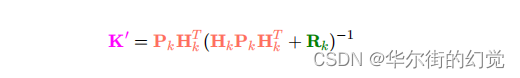
- 实际中的计算⽅法
在实际使⽤卡尔曼滤波的时候，计算的步骤⼀般为：
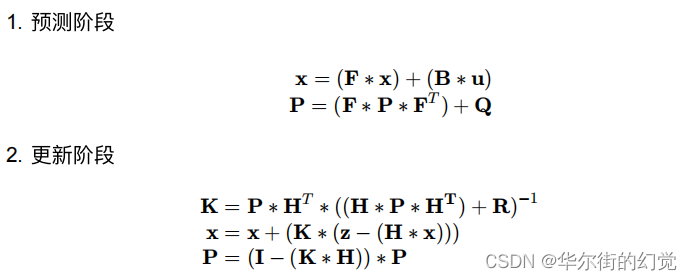
- 最重要的是，我们要时刻关注不断迭代的系统变量，分别是系统的状态：x， 其误差协⽅差矩阵：P，和卡尔曼增益：K。
- 在实际应⽤时，对 xxx 和 xxx 的选择要依据实际情况来定，可以不断调试来寻找 ⼀个最优解，也可以是可变的，只要最终效果能够更好。
3.3.4 小车案例
在利⽤卡尔曼滤波对小车的运动状态进行预测。主要流程如下所示：
- 导入相应的工具包
- 小车运动数据⽣成
- 参数初始化
- 利⽤卡尔曼滤波进⾏小车状态预测
- 可视化：观察参数的变化与结果
下⾯我们看下整个流程实现：
- 导⼊包
from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
from filterpy.kalman import KalmanFilter
- 1
- 2
- 3
- 4
- ⼩⻋运动数据⽣成
在这⾥我们假设⼩⻋作速度为1的匀速运动
# ⽣成1000个位置，从1到1000，是⼩⻋的实际位置
z = np.linspace(1,1000,1000)
# 添加噪声
mu,sigma = 0,1 # mu-期望，sigma-方差
noise = np.random.normal(mu,sigma,1000)
# ⼩⻋位置的观测值
z_nosie = z+noise
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 参数初始化
# dim_x 状态向量size,在该例中为[p,v]，即位置和速度,size=2
# dim_z 测量向量size，假设⼩⻋为匀速，速度为1，测量向量只观测位置，size=1
my_filter = KalmanFilter(dim_x=2, dim_z=1)
# 定义卡尔曼滤波中所需的参数
# x 初始状态为[0,0],即初始位置为0，速度为0.
# 这个初始值不是⾮常重要，在利⽤观测值进⾏更新迭代后会接近于真实值
my_filter.x = np.array([[0.], [0.]])
# p 协⽅差矩阵，表示状态向量内位置与速度的相关性
# 假设速度与位置没关系，协⽅差矩阵为[[1,0],[0,1]]
my_filter.P = np.array([[1., 0.], [0., 1.]])
# F 初始的状态转移矩阵，假设为匀速运动模型，可将其设为如下所示
my_filter.F = np.array([[1., 1.], [0., 1.]])
# Q 状态转移协⽅差矩阵，也就是外界噪声，
# 在该例中假设⼩⻋匀速，外界⼲扰⼩，所以我们对F⾮常确定，觉得F⼀定不会出错，所以Q设的很⼩
my_filter.Q = np.array([[0.0001, 0.], [0., 0.0001]])
# 观测矩阵 Hx = p
# 利⽤观测数据对预测进⾏更新，观测矩阵的左边⼀项不能设置成0
my_filter.H = np.array([[1, 0]])
# R 测量噪声，⽅差为1
my_filter.R = 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 卡尔曼滤波进⾏预测
# 保存卡尔曼滤波过程中的位置和速度
z_new_list = []
v_new_list = []
# 对于每⼀个观测值，进⾏⼀次卡尔曼滤波
for k in range(len(z_nosie)):
# 预测过程
my_filter.predict()
# 利⽤观测值进⾏更新
my_filter.update(z_nosie[k])
# do something with the output
x = my_filter.x
# 收集卡尔曼滤波后的速度和位置信息
z_new_list.append(x[0][0])
v_new_list.append(x[1][0])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 可视化（预测误差、滤波器参数、概率密度函数）
-
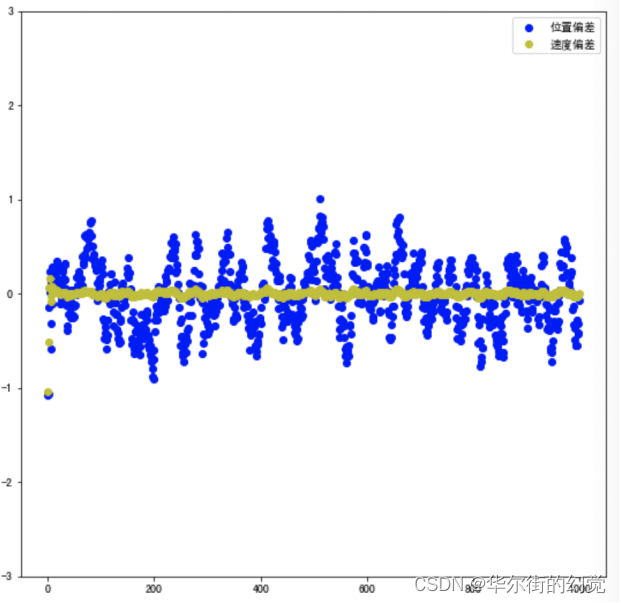
①预测误差的可视化
预测偏差 = 预测结果 - 真实结果# 位移的偏差 dif_list = [] for k in range(len(z)): dif_list.append(z_new_list[k]-z[k]) # 速度的偏差 v_dif_list = [] for k in range(len(z)): v_dif_list.append(v_new_list[k]-1) plt.figure(figsize=(20,9)) plt.subplot(1,2,1) plt.xlim(-50,1050) plt.ylim(-3.0,3.0) plt.scatter(range(len(z)),dif_list,color ='b',label = "位置偏差") plt.scatter(range(len(z)),v_dif_list,color ='y',label = "速度偏差") plt.legend()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
运⾏结果如下所示：
-
② 卡尔曼滤波器参数的变化
⾸先定义⽅法将卡尔曼滤波器的参数堆叠成⼀个矩阵，右下⻆补0，我们看⼀下参数的变化。# 定义⼀个⽅法将卡尔曼滤波器的参数堆叠成⼀个矩阵，右下⻆补0 def filter_comb(p, f, q, h, r): a = np.hstack((p, f)) b = np.array([r, 0]) b = np.vstack([h, b]) b = np.hstack((q, b)) a = np.vstack((a, b)) return a- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
P- 协方差矩阵
F- 状态转移矩阵
Q- 过程激励噪声的协方差矩阵
H - 量测矩阵
R - 测量噪声的协⽅差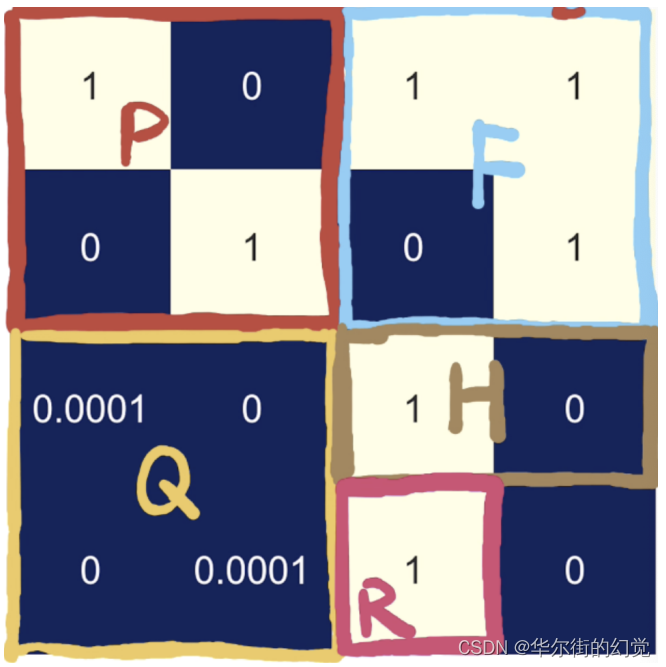
对参数变化进⾏可视化：# 保存卡尔曼滤波过程中的位置和速度 z_new_list = [] v_new_list = [] # 对于每⼀个观测值，进⾏⼀次卡尔曼滤波 for k in range(1): # 预测过程 my_filter.predict() # 利⽤观测值进⾏更新 my_filter.update(z_nosie[k]) # do something with the output x = my_filter.x # 对P、F、Q、H、R五个矩阵进行堆叠 c = filter_comb(my_filter.P,my_filter.F,my_filter.Q,my_filter.H,my_filter.R) # 绘制 plt.figure(figsize=(32,18)) sns.set(font_scale=4) #sns.heatmap(c,square=True,annot=True,xticklabels=False,yticklabels==False sns.heatmap(c,square=True,annot=True,xticklabels=False,yticklabels=False,cbar=False)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
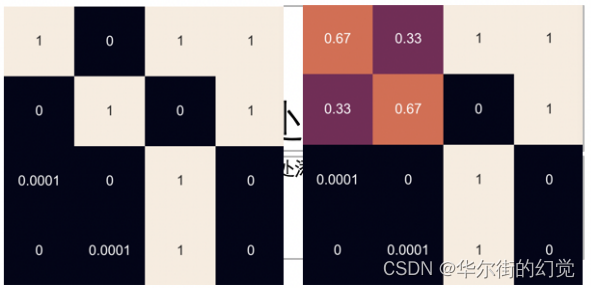
对⽐变换：从图中可以看出变化的P，其他的参数F，Q，H，R为变换。另外状态变量x和卡尔曼系数K也是变化的。
-
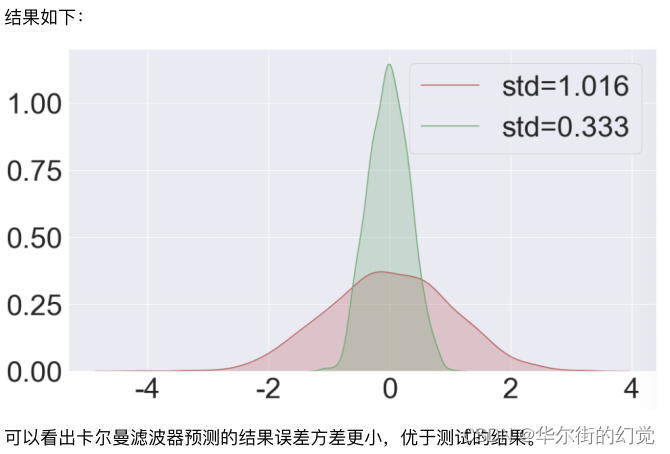
③ 概率密度函数
为了验证卡尔曼滤波的结果 优于 测量的结果，绘制预测结果误差和测量误差的概率密度函数：# ⽣成概率密度图像 z_noise_list_std = np.std(noise) z_noise_list_avg = np.mean(noise) z_filterd_list_std = np.std(dif_list) import seaborn as sns plt.figure(figsize=(16,9)) ax = sns.kdeplot(noise,shade=True,color="r",label="std=%.3f"%z_noise_list_std) ax = sns.kdeplot(dif_list,shade=True,color="g",label="std=%.3f"%z_filterd_list_std)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
-
3.3.5 总结
-
了解filterpy⼯具包
FilterPy是一个实现了各种滤波器的Python模块，它实现著名的卡尔曼滤波和粒子滤波器。直接调用该库完成卡尔曼滤波器实现 -
背景介绍
卡尔曼滤波器通过预测目标在后续帧中的位置，避免在进行目标关联时出现误差 -
卡尔曼滤波器的原理
滤波器根据上一时刻 (k-1 时刻) 的值来估计当前时刻 (k 时刻) 的状态，得到k时刻的先验估计值; 然后使用当前时刻的测量值来更正这个估计值，得到当前时刻的估计值。- 目标不确定性和相关性的度量
- 预测目标的下一时刻的状态
- 系统内部的控制和外部的影响
- 利用观测值进行修正
- 实际应用中：预测和更新两个阶段
-
卡尔曼滤波的实现过程
卡尔曼滤波器的实现，主要分为预测和更新两个阶段，在进行滤波之前，需要先进行初始化- 初始化
预先设定状态变量和观测变量维度、协方差矩阵、运动形式和转换矩阵 - 预测
对状态变量X和协方差P进行预测 - 更新
利用观测结果对卡尔曼滤波的结果进行修征
- 初始化
-
能够利用卡尔曼滤波器完成小车目标状态的预测
- 导入相应的工具包
- 小车运动数据生成： 匀速运动的小车模型
- 参数初始化：对卡尔曼滤波的参数进行初始化，包括状态变量和观测变量维度、协方差矩阵、运动形式和转换矩阵等
- 利用卡尔曼滤波进行小车状态预测：使用Filterpy工具包，调用predict和update完成小车状态的预测
- 可视化：观察参数的变化与结果
- 1.预测误差的分布：p,v
- 2.参数的变化：参数中变化的是X，P，K，不变的是F，Q，H，R
- 3.误差的概率密度函数：卡尔曼预测的结果优于测量结果
3.4 目标估计模型-卡尔曼滤波
学习⽬标
- 了解卡尔曼滤波器中的状态变量和观测输⼊
- 了解⽬标框的状态更新向量
- 了解预测边界框的估计
主要完成卡尔曼滤波器进⾏跟踪的相关内容的实现
- 初始化：卡尔曼滤波器的状态变量和观测输⼊
- 更新状态变量
- 根据状态变量预测⽬标的边界框
3.4.1 初始化
状态量x的设定是⼀个七维向量：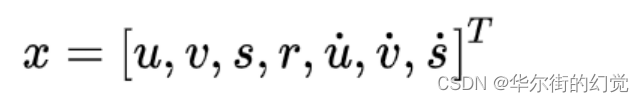
分别表示⽬标中⼼位置的x,y坐标，⾯积s和当前⽬标框的纵横⽐r，最后三个是：横向，纵向，⾯积的变化速率，其中速度部分初始化为0，其他根据观测进⾏输⼊。
初始化卡尔曼滤波器参数，7个状态变量和4个观测输⼊，运动形式和转换矩阵的确定都是基于匀速运动模型，状态转移矩阵F根据运动学公式确定：
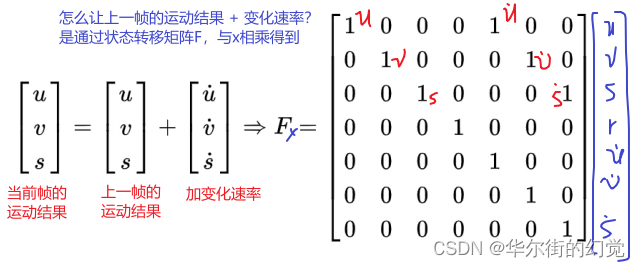
量测矩阵H是4*7的矩阵，将观测值与状态变量相对应：
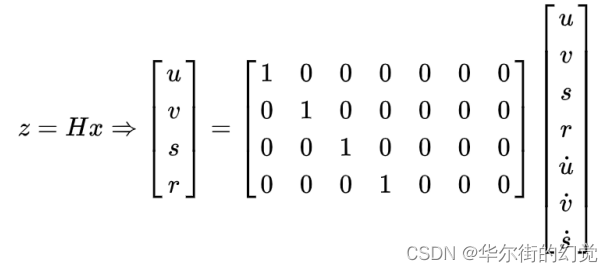
以及相应的协⽅差参数的设定，根据经验值进⾏设定。
def __init__(self, bbox):
# 定义等速模型
# 内部使⽤KalmanFilter，7个状态变量和4个观测输⼊
self.kf = KalmanFilter(dim_x=7, dim_z=4)
# F是状态变换模型，为7*7的⽅阵
self.kf.F = np.array(
[[1, 0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 1]])
# H是量测矩阵，是4*7的矩阵
self.kf.H = np.array(
[[1, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0]])
# R是测量噪声的协⽅差，即真实值与测量值差的协⽅差
self.kf.R[2:, 2:] *= 10.
# P是先验估计的协⽅差
self.kf.P[4:, 4:] *= 1000. # give high uncertainty to the unobserva
self.kf.P *= 10.
# Q是过程激励噪声的协⽅差
self.kf.Q[-1, -1] *= 0.01
self.kf.Q[4:, 4:] *= 0.01
# 状态估计
self.kf.x[:4] = convert_bbox_to_z(bbox)
# 参数的更新
self.time_since_update = 0
self.id = KalmanBoxTracker.count
KalmanBoxTracker.count += 1
self.history = []
self.hits = 0
self.hit_streak = 0
self.age = 0 # 预测的次数
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
3.4.2 更新状态变量
使⽤观测到的⽬标框，更新状态变量（前面估计的结果）
def update(self, bbox):
# 重置
self.time_since_update = 0
# 清空history
self.history = []
# hits计数加1
self.hits += 1
self.hit_streak += 1
# 根据观测结果修改内部状态x
self.kf.update(convert_bbox_to_z(bbox))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
3.4.3 进行目标框的预测
推进状态变量并返回预测的边界框结果
def predict(self):
# 推进状态变量
if (self.kf.x[6] + self.kf.x[2]) <= 0:
self.kf.x[6] *= 0.0
# 进⾏预测
self.kf.predict()
# 卡尔曼滤波的次数
self.age += 1
# 若过程中未更新过，将hit_streak置为0
if self.time_since_update > 0:
self.hit_streak = 0
self.time_since_update += 1
# 将预测结果追加到history中
self.history.append(convert_x_to_bbox(self.kf.x))
return self.history[-1]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
3.4.4 总结
- 了解初始化，卡尔曼滤波器的状态变量和观测输入
- 更新状态变量update()
- 根据状态变量预测目标的边界框predict0
============================
整个代码如下所示：
class KalmanBoxTracker(object):
count = 0
def __init__(self, bbox):
"""
初始化边界框和跟踪器
:param bbox:
"""
# 定义等速模型
# 内部使⽤KalmanFilter，7个状态变量和4个观测输⼊
self.kf = KalmanFilter(dim_x=7, dim_z=4)
# F是状态变换模型，为7*7的⽅阵
self.kf.F = np.array(
[[1, 0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 1]])
# H是量测矩阵，是4*7的矩阵
self.kf.H = np.array(
[[1, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0]])
# R是测量噪声的协⽅差，即真实值与测量值差的协⽅差
self.kf.R[2:, 2:] *= 10.
# P是先验估计的协⽅差
self.kf.P[4:, 4:] *= 1000. # give high uncertainty to the unobserva
self.kf.P *= 10.
# Q是过程激励噪声的协⽅差
self.kf.Q[-1, -1] *= 0.01
self.kf.Q[4:, 4:] *= 0.01
# 状态估计
self.kf.x[:4] = convert_bbox_to_z(bbox)
# 参数的更新
self.time_since_update = 0
self.id = KalmanBoxTracker.count
KalmanBoxTracker.count += 1
self.history = []
self.hits = 0
self.hit_streak = 0
self.age = 0 # 预测的次数
def update(self, bbox):
"""
使⽤观察到的⽬标框更新状态向量。filterpy.kalman.KalmanFilter.update 会根据观测
重置self.time_since_update，清空self.history。
:param bbox:⽬标框
:return:
"""
# 重置
self.time_since_update = 0
# 清空history
self.history = []
# hits计数加1
self.hits += 1
self.hit_streak += 1
# 根据观测结果修改内部状态x
self.kf.update(convert_bbox_to_z(bbox))
def predict(self):
"""
推进状态向量并返回预测的边界框估计。
将预测结果追加到self.history。由于 get_state 直接访问 self.kf.x，所以self.his
:return:
"""
# 推进状态变量
if (self.kf.x[6] + self.kf.x[2]) <= 0:
self.kf.x[6] *= 0.0
# 进⾏预测
self.kf.predict()
# 卡尔曼滤波的次数
self.age += 1
# 若过程中未更新过，将hit_streak置为0
if self.time_since_update > 0:
self.hit_streak = 0
self.time_since_update += 1
# 将预测结果追加到history中
self.history.append(convert_x_to_bbox(self.kf.x))
return self.history[-1]
def get_state(self):
"""
返回当前边界框估计值(转为左上角/右下角坐标)
:return:
"""
return convert_x_to_bbox(self.kf.x)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
3.5 匈牙利算法
学习目标:
- 了解匈牙利算法
- 了解KM算法
匈牙利算法 (Hungarian Agorithm) 与KM算法 (Kuhn-Munkres Algorithm) 是用来解决多目标跟踪中的数据关联问题，匈牙利算法与KM算法都是为了求解二分图的最大匹配问题。
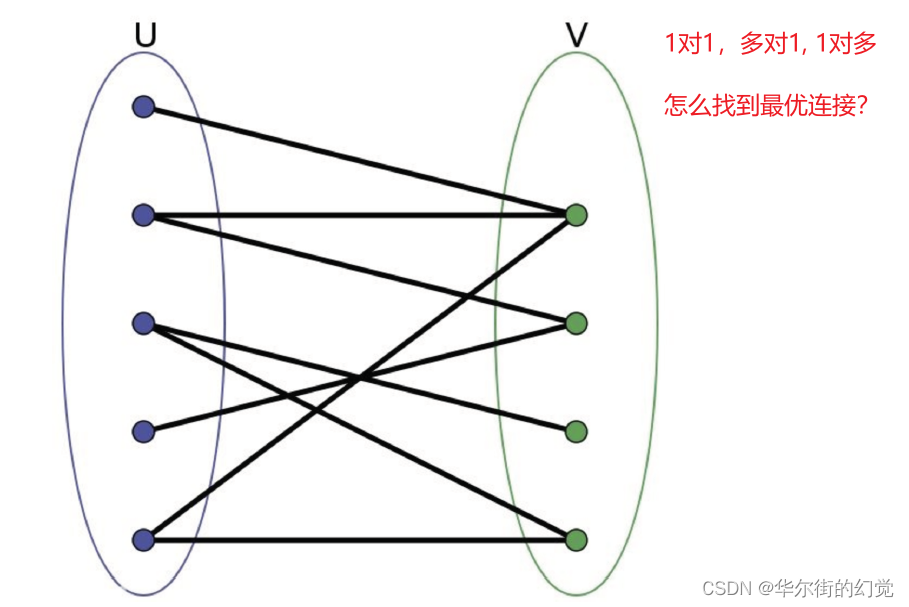
有一种很特别的图，就做二分图，那什么是二分图呢? 就是能分成两组，U,V。其中，U上的点不能相互连通，只能连去V中的点，同理，V中的点不能相互连通，只能连去U中的点。这样，就叫做二分图。
可以把二分图理解为视频中连续两帧中的所有检测框，第一顿所有检测框的集合称为U，第二帧所有检测框的集合称为V。同一帧的不同检测框不会为同一个目标所以不需要互相关联，相邻两帧的检测框需要相互联通，最终将相邻两帧的检测框尽量完美地两两匹配起来。而求解这个问题的最优解就要用到匈牙利算法或者KM算法。
3.5.1 匈牙利算法
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法。美国数学家哈罗德·库恩于1955年提出该算法。此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Denes K6nig和Jen Egervary的工作之上创建起来的。
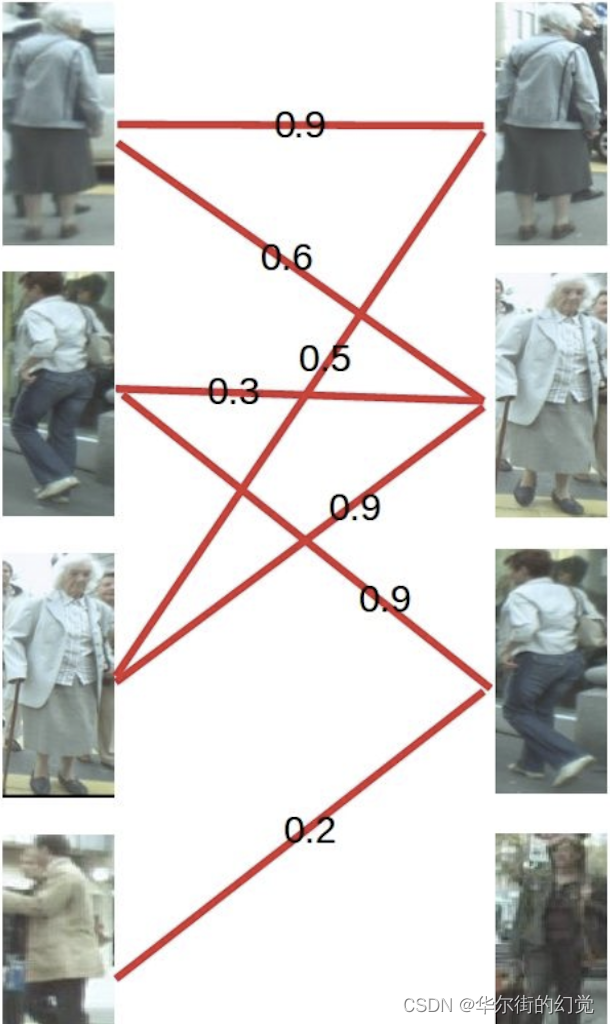
我们以目标跟踪的方法介绍匈牙利算法，以下图为例，假设左边的四张图是我们在第N帧检测到的目标 (U)，右边四张图是我们在第N+1检测到的目标 (V) 。红线连起来的图，是我们的算法认为是同一行人可能性较大的目标。由于算法并不是绝对理想的，因此并不一定会保证每张图都有一对一的匹配，一对二甚至一对多,再甚至多对多的情况都时有发生。这时我们怎么获得最终的一对一跟踪结果呢? 我们来看匈牙利算法是怎么做的。
- 第一步
首先给左1进行匹配，发现第一个与其相连的右1还未匹配，将其配对，连上一条蓝线。
- 第二步
接着匹配左2，发现与其相连的第一个目标右2还未匹配，将其配对
- 第三步
接下来是左3，发现最优先的目标右1已经匹配完成了，怎么办呢?我们给之前右1的匹配对象左1分配另一个对象。(黄色表示这条边被临时拆掉)
可以与左1匹配的第二个目标是右2，但右2也已经有了匹配对象，怎么办呢?我们再给之前右2的匹配对象左2分配另一个对象 (注意这个步骤和上面是一样的这是一个递归的过程)
此时发现左2还能匹配右3，那么之前的问题迎刃而解了，回溯回去左2对右3，左1对右2，左3对右1。
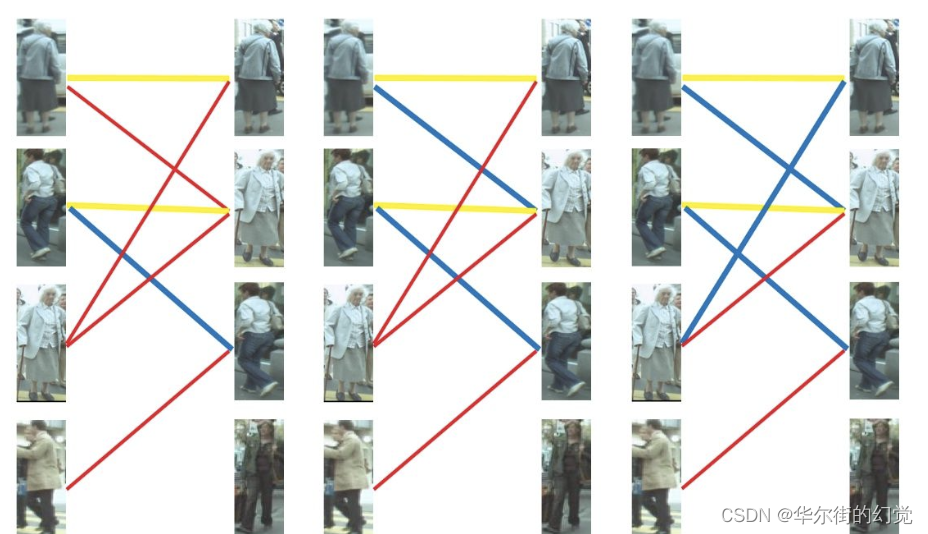
所以第三步最后的结果就是：
- 第四步
最后是左4，很遗憾，按照第三步的节奏我们没法给左4腾出来一个匹配对象，只能放弃对左4的匹配，匈牙利算法流程至此结束。蓝线就是我们最后的匹配结果。至此我们找到了这个二分图的一个最大匹配。最终的结果是我们匹配出了三对目标，由于候选的匹配目标中包含了许多错误的匹配红线(边)，所以匹配准率并不高。可见匈牙利算法对红线连接的准确率要求很高，也就是要求我们运动模型、外观模型等部件必须进行较为精准的预测，或者预设较高的闻值，只将置信度较高的边才送入匈牙利算法进行匹配，这样才能得到较好的结果。
匈牙利算法的流程大家看到了，有一个很明显的问题相信大家也发现了，按这个思路找到的最大匹配往往不是我们心中的最优。匈牙利算法将每个匹配对象的地位视为相同，在这个前提下求解最大匹配。这个和我们研究的多目标跟踪问题有些不合，因为每个匹配对象不可能是同等地位的，总有一个真实目标是我们要找的最佳匹配，而这个真实目标应该拥有更高的权重，在此基础上匹配的结果才能更贴近真实情况。
KM算法就能比较好地解决这个问题，我们下面来看看KM算法
3.5.2 KM算法
KM算法解决的是带权二分图的最优匹配问题
还是用上面的图来举例子，这次给每条连接关系加入了权重，也就是我们算法中其他模块给出的置信度分值。
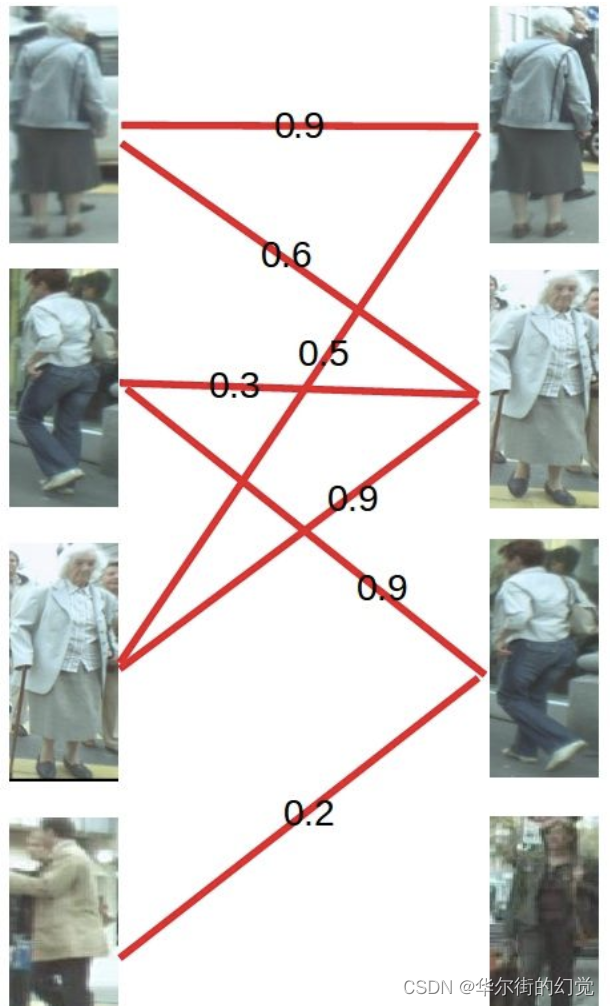
KM算法解决问题的步骤是这样的。
- 第一步
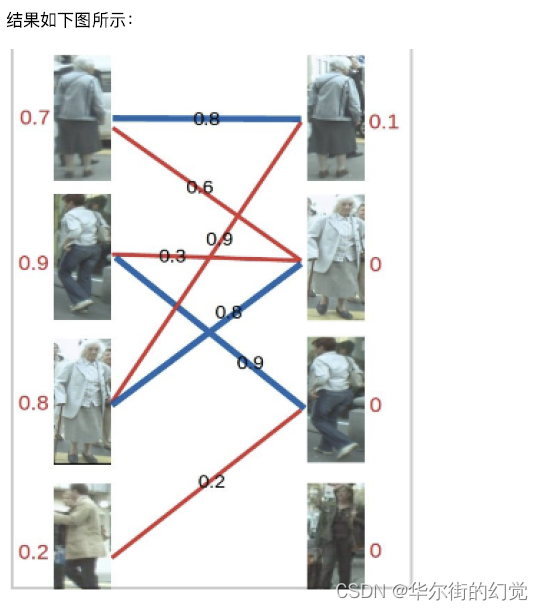
首先对每个顶点默值，称为顶标，将左边的顶点赋值为与其相连的边的最大权重，右边的顶点赋值为0。
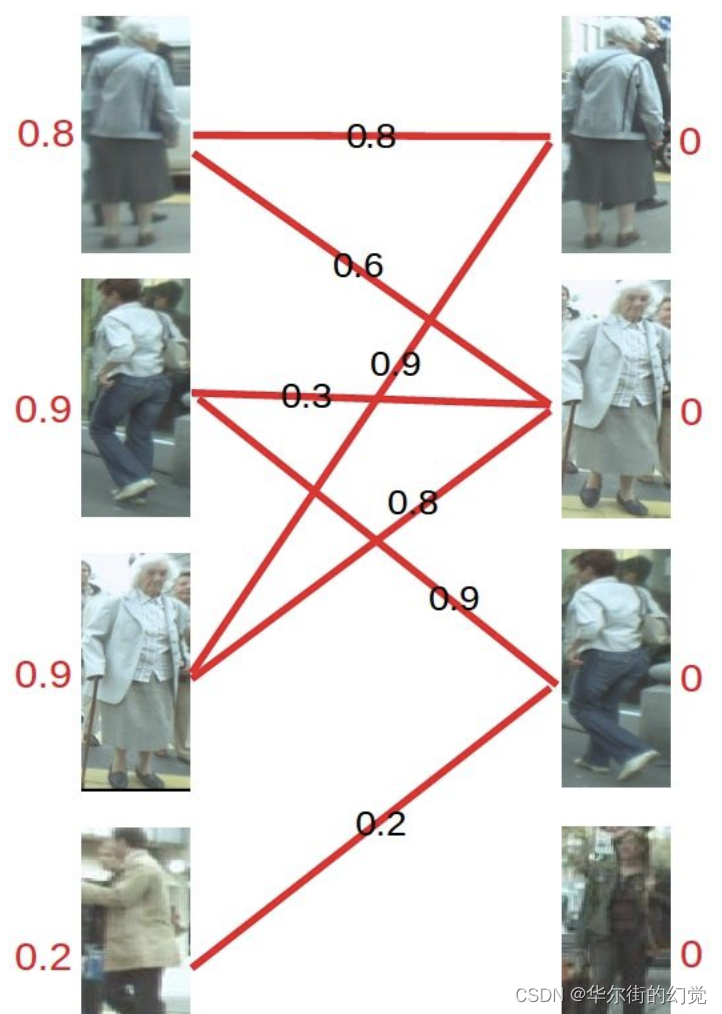
- 第二步
匹配的原则是只和权重与左边分数(顶标)相同的边进行匹配，若找不到边匹配对此条路径的所有左边顶点的顶标减d，所有右边顶点的顶标加d。参数d（超参数）我们在这里取值为0.1。
对于左1，与顶标分值相同的边先标蓝
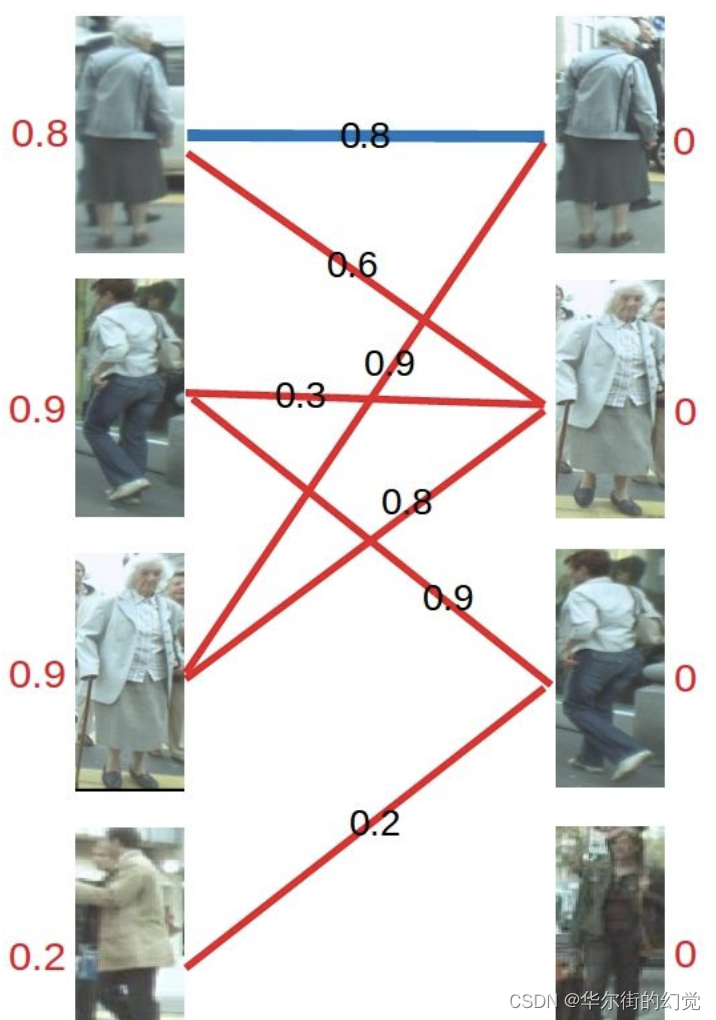
然后是左2，与顶标分值相同的边标
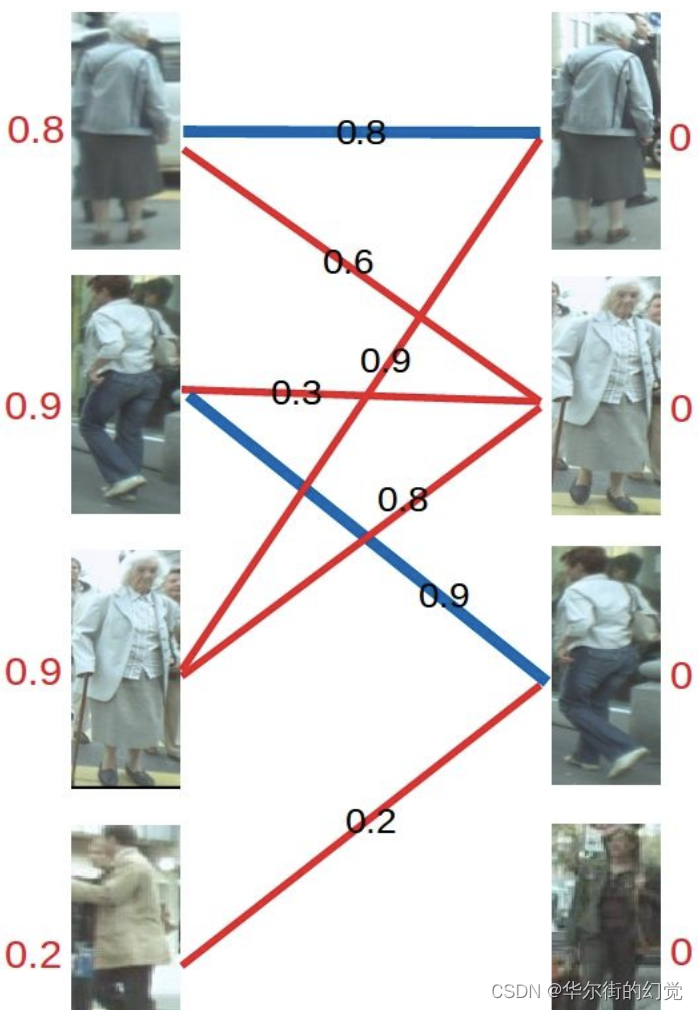
然后是左3，发现与右1已经与左1配对。首先想到让左3更换匹配对象，然而根据匹配原则，只有权值大于等于0.9+0=0.9 (左顶标加右顶标)的边能满足要求。于是左3无法换边。那左1能不能换边呢? 对于左1来说，只有权值大于等于0.8+0=0.8的边能满足要求，无法换边。此时根据KM算法，应对所有冲突的边的顶点做加减操作，令左边顶点值减0.1，右边顶点值加0.1。结果如下图所示。
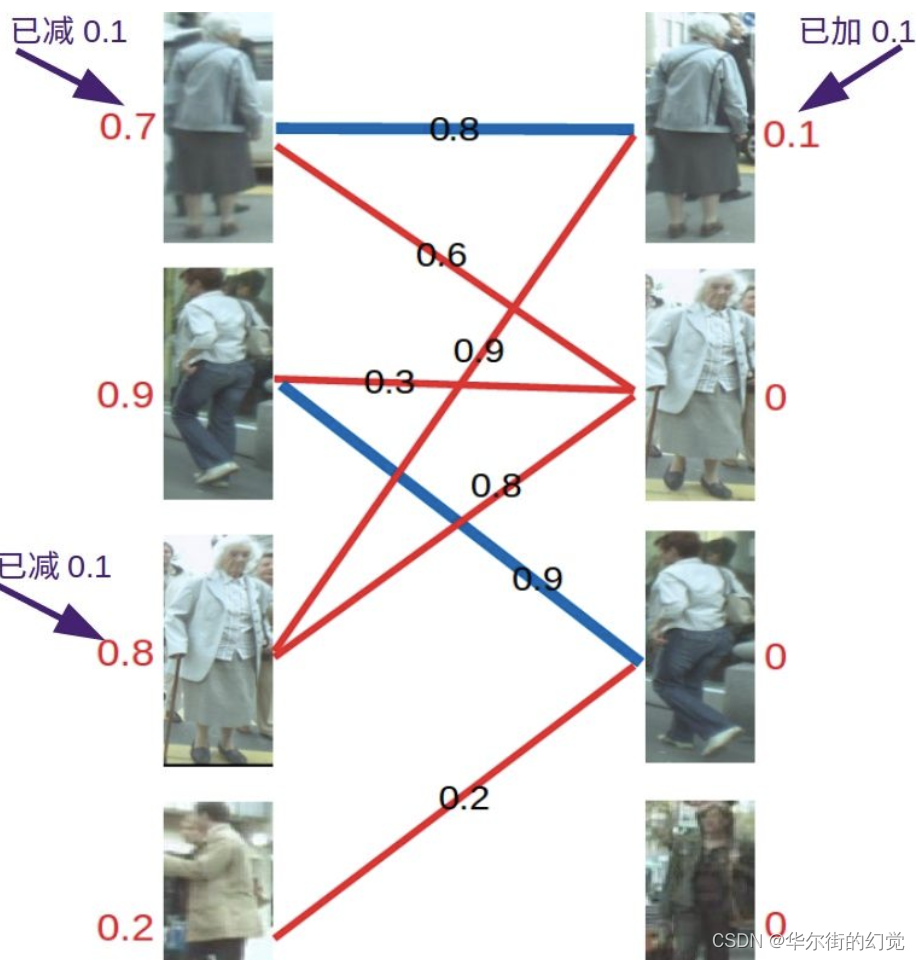再进行匹配操作，发现左3多了一条可匹配的边，因为此时左3对右2的匹配要求只需权重大于等于0.8+0即可，所以左3与右2匹配
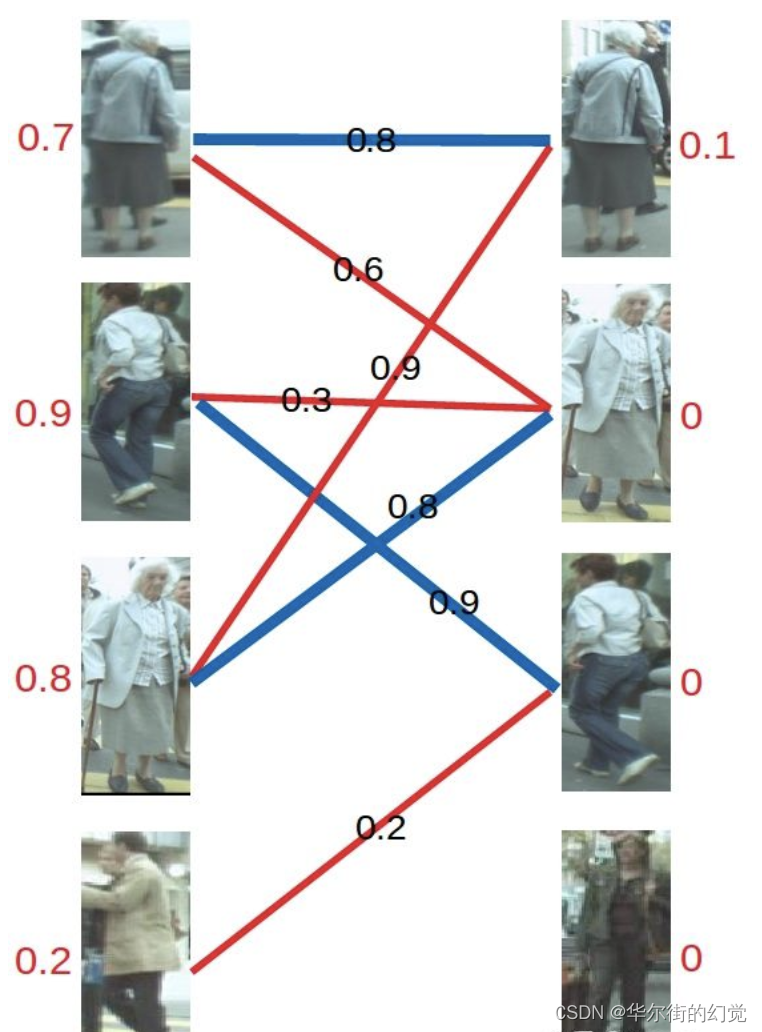最后进行左4的匹配，由于左4唯一的匹配对象右3已被左2匹配，发生冲突。进行-轮加减d操作，再匹配，左四还是匹配失败。两轮以后左4期望值降为0，放弃匹配左4。
至此KM算法流程结束，三对目标成功匹配，甚至在左三目标预测不够准确的情况下也进行了正确匹配。可见在引入了权重之后，匹配成功率大大提高。
最后还有一点值得注意，匈牙利算法得到的最大匹配并不是唯一的，预设匹配边或者匹配顺序不同等，都可能会导致有多种最大匹配情况，所以有一种替代KM算法的想法是，我们只需要用匈牙利算法找到所有的最大匹配，比较每个最大匹配的权重，再选出最大权重的最优匹配即可得到更贴近真实情况的匹配结果。但这种方法时间复杂度较高，会随着目标数越来越多，消耗的时间大大增加，实际使用中并不推荐。
3.5.3 匈牙利算法的实现
使用：
scipy.optimize.linear_sum_assignment(cost_matrix)
- 1
希望用最小代价实现匹配，所以是相似度矩阵求负号，进行线性规划
实现KM算法，其中const matrix表示代价矩阵。比如第一帧有a,b,c,d四个目标，第二顿图像有p,q,r,s四个目标，其相似度矩阵如下所示：
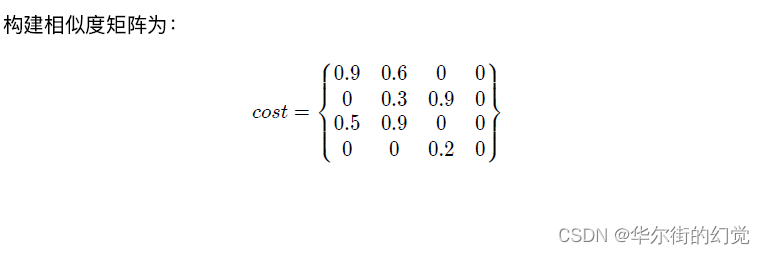
from scipy.optimize import linear_sum_assignment
import numpy as np
# 代价矩阵
cost =np.array([[0.9,0.6,0,0],[0,0.3,0.9,0],[0.5,0.9,0,0],[0,0,0.2,0]])
# 匹配结果：该⽅法的⽬的是代价最⼩，这⾥是求最⼤匹配，所以将cost取负数
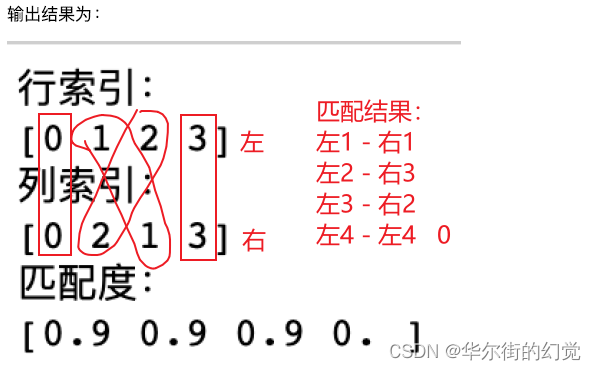
row_ind,col_ind=linear_sum_assignment(-cost)
#对应的⾏索引
print("⾏索引：\n{}".format(row_ind))
#对应⾏索引的最优指派的列索引
print("列索引：\n{}".format(col_ind))
#提取每个⾏索引的最优指派列索引所在的元素，形成数组
print("匹配度：\n{}".format(cost[row_ind,col_ind]))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
3.5.4 总结
- 匈牙利算法和KM算法是进行二分图最大匹配的算法，在目标追踪用于进行目标关联
3.6 数据关联
学习目标
- 利用匈牙利算法对目标框和检测框进行关联
主要思想：在这里我们对检测框和跟踪框进行匹配，整个流程是遍历检测框和跟踪框，并进行匹配，匹配成功的将其保留，未成功的将其删除。
该数据关联函数有3个输入和3个输出
- 3个输入
- detections:检测框
- trackers:跟踪框
- iou_threshold:IOU阈值,大于阈值即我们匹配的目标，小于阈值即没匹配成功(前后两帧的目标不是同一个)
- 3个输出
- 跟踪成功⽬标的矩阵：matchs
- 新增⽬标的矩阵：unmatched_detections
- 跟踪失败即离开画⾯的⽬标矩阵：unmatched_trackers
# 将yolo模型的检测框和卡尔曼滤波的跟踪框进行匹配
def associate_detections_to_trackers(detections, trackers, iou_threshold=0.3):
"""
将检测框bbox与卡尔曼滤波器的跟踪框进⾏关联匹配
:param detections:检测框
:param trackers:跟踪框，即跟踪⽬标
:param iou_threshold:IOU阈值,大于阈值即我们匹配的目标，小于阈值即没匹配成功(前后两帧的目标不是同一个)
:return:跟踪成功⽬标的矩阵：matchs
新增⽬标的矩阵：unmatched_detections
跟踪失败即离开画⾯的⽬标矩阵：unmatched_trackers
"""
# [Step1] 跟踪⽬标/跟踪目标数量为0，直接构造结果
if (len(trackers) == 0) or (len(detections) == 0):
return np.empty((0, 2), dtype=int), np.arange(len(detections)), np.empty((0,5),dtype=int)
# [Step2] 如何评估检测框和跟踪框的相似度-IOU
# iou 不⽀持数组计算。逐个计算两两间的交并⽐，调⽤ linear_assignment 进⾏匹配
# 创造全0数组(行-检测框的个数, 列-跟踪框的个数),存储IOU交并比矩阵
iou_matrix = np.zeros((len(detections), len(trackers)), dtype=np.float32)
# 遍历⽬标检测的bbox集合，每个检测框的标识为d
for d, det in enumerate(detections):
# 遍历跟踪框（卡尔曼滤波器预测）bbox集合，每个跟踪框标识为t
for t, trk in enumerate(trackers):
iou_matrix[d, t] = iou(det, trk) # 检测框和跟踪框的交并比
# 通过匈⽛利算法将跟踪框和检测框以[[d,t]...]的⼆维矩阵的形式存储在match_indices中
result = linear_sum_assignment(-iou_matrix) # result由行索引、列索引组成，检测框和跟踪框匹配后的行、列索引
matched_indices = np.array(list(zip(*result)))
# [Step3] 记录返回的结果
# [Step3.1] 记录未匹配的检测框
# 未匹配的检测框放⼊unmatched_detections中，表示有新的⽬标进⼊画⾯，要新增跟踪器跟踪⽬
unmatched_detections = [] # 新建空列表
for d, det in enumerate(detections):
if d not in matched_indices[:, 0]: # 没匹配成功
unmatched_detections.append(d) # 增加索引
# [Step3.2] 记录未匹配的跟踪框
# 未匹配的跟踪框放⼊unmatched_trackers中，表示⽬标离开之前的画⾯，应删除对应的跟踪器
unmatched_trackers = []
for t, trk in enumerate(trackers):
if t not in matched_indices[:, 1]:
unmatched_trackers.append(t)
# [Step3.3] 记录匹配的检测框和跟踪框
# 将匹配成功的跟踪框放⼊matches中
matches = []
for m in matched_indices:
# [低于阈值] 过滤掉IOU低的匹配，将其放⼊到unmatched_detections和unmatched_trackers
if iou_matrix[m[0], m[1]] < iou_threshold:
unmatched_detections.append(m[0])
unmatched_trackers.append(m[1])
# [大于阈值] 才算匹配成功,满⾜条件的以[[d,t]...]的形式放⼊matches中
else:
matches.append(m.reshape(1, 2))
# [Step4] 构建返回的结果
# 初始化matches,以np.array的形式返回
if len(matches) == 0:
matches = np.empty((0, 2), dtype=int)
else:
matches = np.concatenate(matches, axis=0)
return matches, np.array(unmatched_detections), np.array(unmatched_trackers)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 总结：
利⽤匈⽛利算法完成⽬标检测框和跟踪框的匹配
3.7 SORT/deepSORT
学习目标:
- 理解SORT算法的原理
- 理解DeepSORT算法的原理
上一节给大家介绍了一下多目标跟踪MOT的一些基础知识。SORT和DeepSORT是多目标跟踪中两个知名度比较高的算法。DeepSORT是原团队对SORT的改进版本。现在来解析一下SORT和DeepSORT的基本思路。
3.7.1 SORT
SORT核心是卡尔曼滤波和匈牙利匹配两个算法。流程图如下所示，可以看到整体可以拆分为两个部分，分别是匹配过程和卡尔曼预测加更新过程，都用灰色框标出来了。
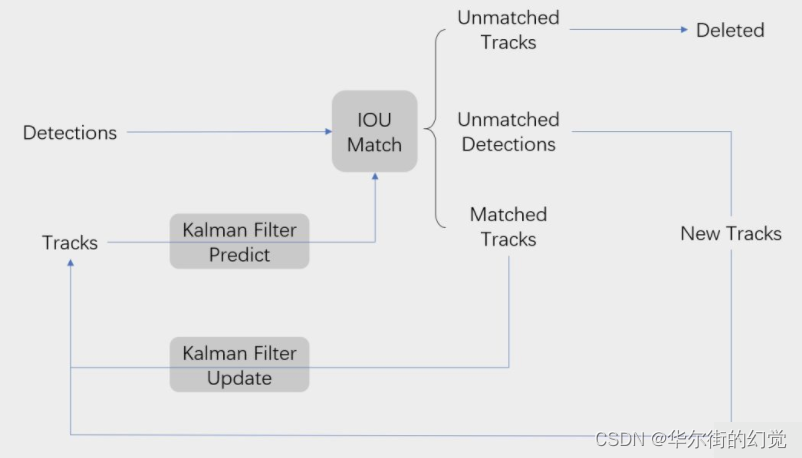
SORT算法的关键步骤:轨迹卡尔曼滤波预测一 使用匈牙利算法将预测后的tracks 和 当前帧中的detecions进行匹配(IOU匹配)，卡尔曼滤波更新
卡尔曼滤波分为两个过程：预测和更新。SORT引入了线性速度模型与卡尔曼滤波来进行位置预测，先进行位置预测然后再进行匹配。运动模型的结果可以用来预测物体的位置。
匈牙利算法解决的是一个分配问题，用IOU距离作为权重 (也叫cost矩阵)，并且当IOU小于一定数值时，不认为是同一个目标，理论基础是视频中两帧之间物体移动不会过多。在代码中选取的阙值是0.3。scipy库的linear_sum_assignment都实现了这一算法，只需要输入cost_matrix即代价矩阵就能得到最优匹配。
3.7.2 DeepSORT
DeepSORT是SORT的续作，整体框架没有大改，还是延续了卡尔曼滤波加匈牙利算法的思路，在这个基础上增加了鉴别网络Deep Association Metric（行人重识别）
下图是deepSORT流程图，和SORT基本一样，就多了级联匹配(MatchingCascade) 和新轨迹的确认 (confirmed)
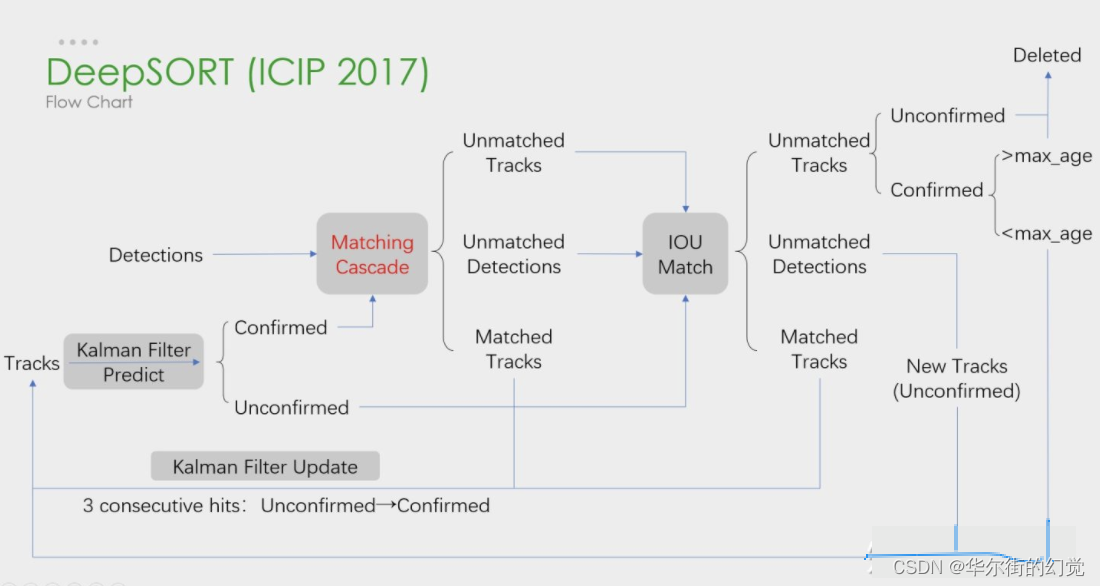DeepSORT算法的关键步骤:轨迹卡尔曼滤波预测一 使用牙利算法将预测后的tracks和当前顿中的detecions进行匹配 (级联匹配和IOU匹配)，卡尔曼滤波更新
级联匹配：
- Matched Tracks匹配到的放Tracks中
- unmatched Detections放到Unconfirmed的跟踪框中匹配
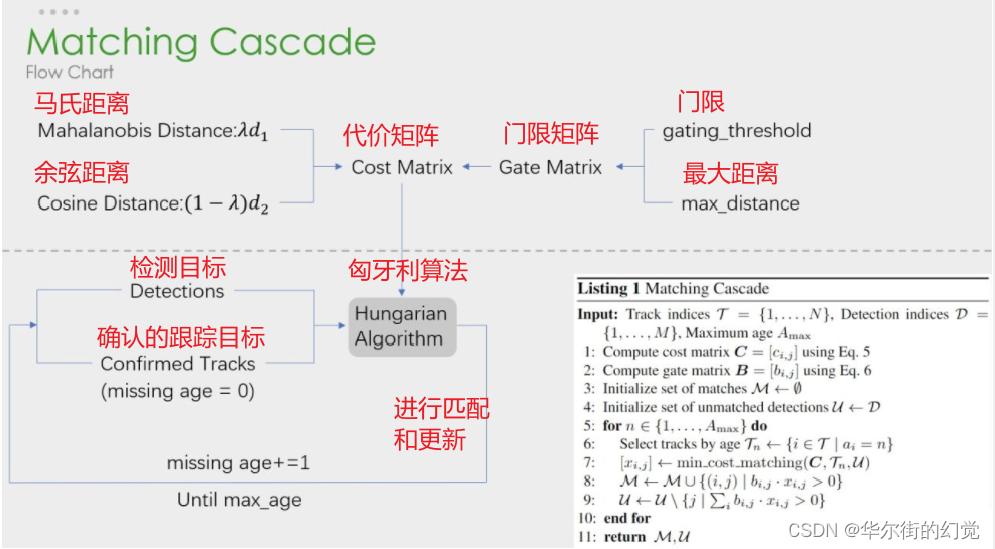
其中上半部分就是相似度估计，也就是算这个分配问题的代价函数。下半部分依旧使用匈牙利算法进行检测框和跟踪框的匹配。
3.7.3 总结
- SORT算法
SORT是利用强大的CNN检测器的检测结果来进行多目标跟踪使用基于卡尔曼滤波(Kalman filter) 与匈牙利算法 (Hungarian algorithm) 的方法来进行跟踪 - DeepSORT算法
DeepSORT是在SORT基础上进行的修改，增加了级联匹配和目标的确认，还是使用卡尔曼滤波加匈牙利算法进行目标跟踪
3.8 多目标跟踪
学习目标
- 利用sort算法完成多目标追踪
主要实现了一个多目标跟踪器，管理多个卡尔曼滤波器对象，主要包括以下内容:
- 初始化:最大检测数，目标未被检测的最大顿数
- 目标跟踪结果的更新，即跟踪成功和失败的目标的更新
- 初始化
def __init__(self, max_age=1, min_hits=3): """ 初始化：设置SORT算法的关键参数 :param max_age:最⼤检测数，当目标消失超过该数，就删除该目标 :param min_hits:最小次数，最少要超过该数，才认为该目标在跟踪当中 """ # 最⼤检测数：⽬标未被检测到的帧数，超过之后会被删 self.max_age = max_age # ⽬标命中的最⼩次数，⼩于该次数不返回 self.min_hits = min_hits # 卡尔曼跟踪器 self.trackers = [] # 帧计数 self.frame_count = 0- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 目标跟踪结果的更新:
该方法实现了SORT算法，输入是当前帧中所有物体的检测框的集合，包括目标的score，输出是当前顿标的跟踪框集合，包括目标的跟踪的id要求是即使检测框为空，也必须对每一帧调用此方法，返回一个类似的输出数组，最后一列是目标对像的id。需要注意的是，返回的目标对象数量可能与检测框的数量不同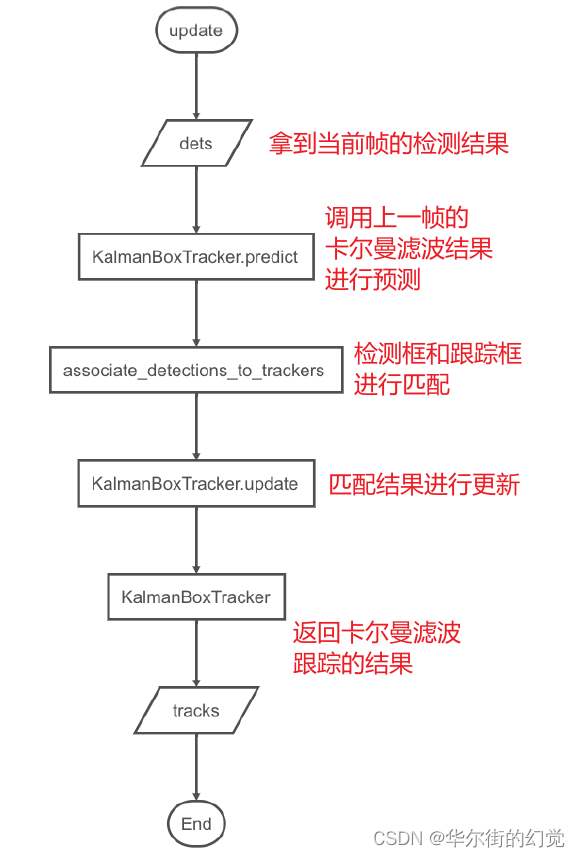
我们将上述两个⽅法封装在⼀个类中。
class Sort(object):
def __init__(self, max_age=1, min_hits=3):
"""
初始化：设置SORT算法的关键参数
:param max_age:最⼤检测数，当目标消失超过该数，就删除该目标
:param min_hits:最小次数，最少要超过该数，才认为该目标在跟踪当中
"""
# 最⼤检测数：⽬标未被检测到的帧数，超过之后会被删
self.max_age = max_age
# ⽬标命中的最⼩次数，⼩于该次数不返回
self.min_hits = min_hits
# 卡尔曼跟踪器
self.trackers = []
# 帧计数:当前处理了多少帧
self.frame_count = 0
def update(self, dets):
self.frame_count += 1 # 到了新一帧的图像
# [Step 1] 获取卡尔曼滤波的跟踪框结果
# 在当前帧逐个预测轨迹位置，记录状态异常的跟踪器索引
# 根据当前所有的卡尔曼跟踪器个数（即上⼀帧中跟踪的⽬标个数）创建⼆维数组
# ⼆维数组：⾏号为卡尔曼滤波器的标识, 列向量为跟踪框的位置和ID(坐标+ID,所以是5)
trks = np.zeros((len(self.trackers), 5)) # 存储跟踪器的预测
to_del = [] # 存储要删除的⽬标框
ret = [] # 存储要返回的追踪⽬标框
# 循环遍历卡尔曼跟踪器列表
for t, trk in enumerate(trks):
# 使⽤第t个卡尔曼跟踪器产⽣对应⽬标的跟踪框,pos是目标框的位置
pos = self.trackers[t].predict()[0]
# 遍历完成后，trk中存储了上⼀帧中跟踪的⽬标的预测跟踪框
trk[:] = [pos[0], pos[1], pos[2], pos[3], 0] # 左上角坐标2个，右下角坐标2个，置信度0
# 如果跟踪框中包含空值，则将该跟踪框添加到要删除的列表中
if np.any(np.isnan(pos)):
to_del.append(t)
# numpy.ma.masked_invalid 屏蔽出现⽆效值的数组（NaN 或 inf）
# numpy.ma.compress_rows 压缩包含掩码值的2-D 数组的整⾏，将包含掩码值的整⾏
# trks中存储了上⼀帧中跟踪的⽬标 并且 在当前帧中的预测跟踪框
trks = np.ma.compress_rows(np.ma.masked_invalid(trks))
# 逆向删除异常的跟踪器，防⽌破坏索引
for t in reversed(to_del): # 反向遍历
self.trackers.pop(t)
# [Step 2] 数据关联：利⽤匈⽛利算法对⽬标检测框和目标跟踪框进⾏关联
# 将⽬标检测框与卡尔曼滤波器预测的跟踪框关联获取跟踪成功的⽬标，新增的⽬标，离开画面的目标
matched, unmatched_dets, unmatched_trks = associate_detections_to_trackers(dets, trks)
# [Step 3] 对匹配结果的处理
# [Step 3.1]将跟踪成功的⽬标框，更新到对应的卡尔曼滤波器
for t, trk in enumerate(self.trackers):
if t not in unmatched_trks:
d = matched[np.where(matched[:, 1] == t)[0], 0]
# 使⽤观测的边界框更新状态向量
trk.update(dets[d, :][0])
# [Step 3.2]为新增的⽬标，创建新的卡尔曼滤波器对象进⾏跟踪
for i in unmatched_dets:
trk = KalmanBoxTracker(dets[i, :])
self.trackers.append(trk)
#
# ⾃后向前遍历，仅返回 (1)在当前帧出现 (2)且命中周期⼤于self.min_hits（除⾮跟踪刚开始)的跟踪结果
# 如果未命中时间大于self.max_age则删除跟踪器
# hit_streak忽略⽬标初始的若⼲帧
i = len(self.trackers)
for trk in reversed(self.trackers): # 反转遍历
# 返回当前边界框的估计值
d = trk.get_state()[0]
# 跟踪成功⽬标的box与id放⼊ret列表中
if (trk.time_since_update < 1) and \
(trk.hit_streak >= self.min_hits or self.frame_count<=self.max_age):
ret.append(np.concatenate((d, [trk.id + 1])).reshape(1, -1))
i -= 1
# 跟踪失败或离开画⾯的⽬标从卡尔曼跟踪器中删除
if trk.time_since_update > self.max_age:
self.trackers.pop(i)
# 返回当前画⾯中所有⽬标的box与id,以⼆维矩阵形式返回
if len(ret) > 0:
return np.concatenate(ret)
# 若要返回的追踪⽬标框的长度为0,,则返回空数组
return np.empty((0, 5))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
总结
了解sort进⾏多⽬标跟踪的实现
3.9 基于YoloV3的目标检测
学习目标
- 知道yoloV3的多尺度检测方法
- 知道yoloV3模型的网络结构及网络输出
- 了解yoloV3模型先验框设计的方法
- 知道yoloV3模型为什么适用于多标签的目标分类
- 熟悉利用yolo模型进行目标检测的方法
- 能够完成目标检测功能的实现
yoloV3以V1，V2为基础进行的改进，主要有: 利用多尺度特征进行目标测; 先验框更丰富; 调整了网络结构; 对象分类使用logistic代替了softmax,更适用于多标签分类任务。
3.9.1 YoloV3算法简介
YOLOv3是YOLO(You Only Look Once)系列目标检测算法中的第三版，相比之前的算法，尤其是针对小目标，精度有显著提升。
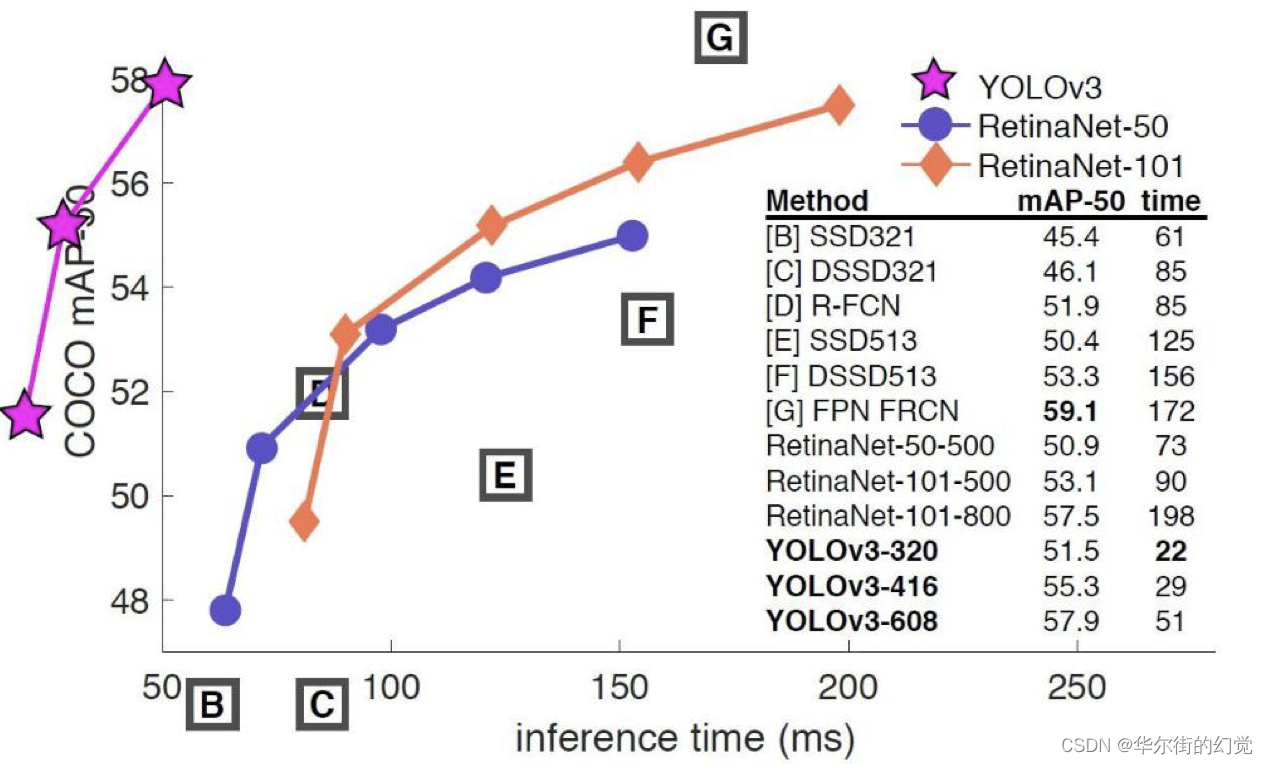
yoloV3的流程如下图所示，对于每一幅输入图像，YOLOv3会预测三个不同尺度的输出，目的是检测出不同大小的目标
- 黑框 - 图像分成很多小块
- 黄框 - 每个小块生成先验框，检测目标
- 红框 - 对特定目标，中心落在某个黑框的时候，黑框就负责检测该目标
3.9.2 多尺度检测
通常一幅图像包含各种不同的物体，并且有大有小。比较理想的是一次就可以将所有大小的物体同时检测出来。因此，网络必须具备能够“看到”不同大小的物体的能力。因为网络越深，特征图就会越小，所以网络越深小的物体也就越难检测出来。
在实际的feature map中，随着网络深度的加深，浅层的feature map中主要包含低级的信息(物体边缘，颜色，初级位置信息等)，深层的feature map中包含高等信息 (例如物体的语义信息: 狗，猫，汽车等等)。因此在不同级别的featuremap对应不同的scale，所以我们可以在不同级别的特征图中进行目标检测。如下图展示了多种scale变换的经典方法。
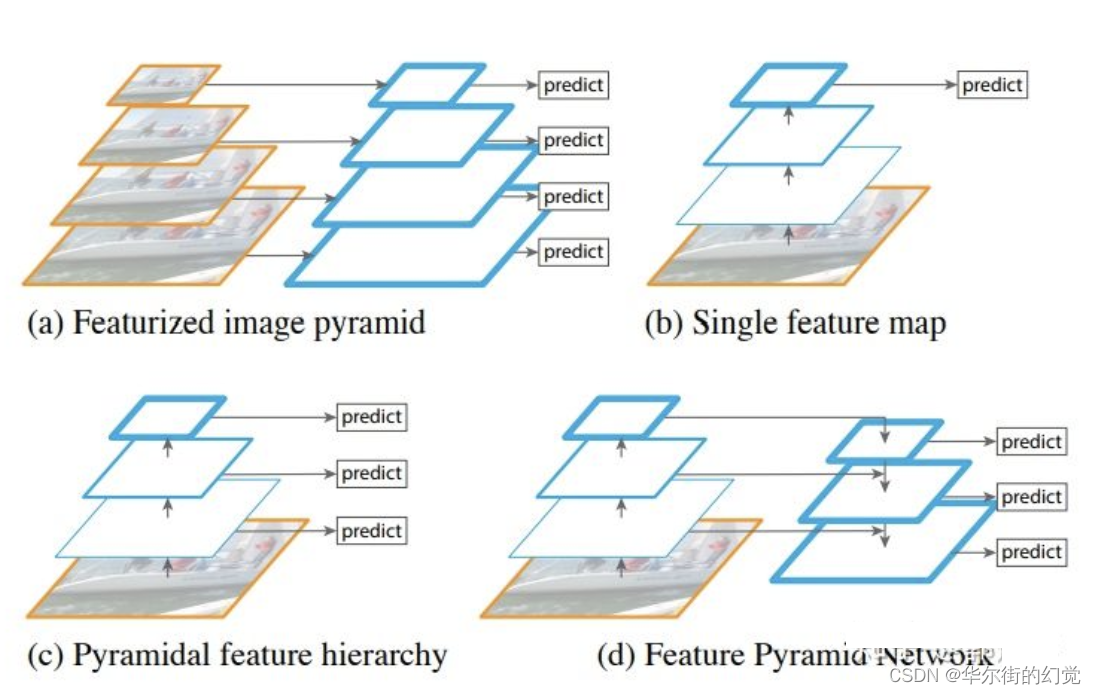(a) 这种方法首先建立图像金字塔，不同尺度的金字塔图像被输入到对应的网络当中，用于不同scale物体的检测。但这样做的结果就是每个级别的金字塔都需要进行一次处理，速度很慢，在SPPNet使用的就是这种方式
(b)检测只在最后一层feature map阶段进行，这个结构无法检测不同大小的物体
© 对不同深度的feature map分别进行目标检测。SSD中采用的便是这样的结构。这样小的物体会在浅层的feature map中被检测出来，而大的物体会在深层的feature map被检测出来，从而达到对应不同scale的物体的目的，缺点是每一个feature map获得的信息仅来源于之前的层，之后的层的特征信息无法获取并加以利用。
(d) 与©很接近，但不同的是，当前层的feature map会对未来层的feature map进行上采样，并加以利用。因为有了这样一个结构，当前的feature map就可以获得“未来”层的信息，这样的话低阶特征与高阶特征就有机融合起来了，提升检测精度。在YOLOv3中，就是采用这种方式来实现目标多尺度的变换的。
3.9.3 网络模型结构
在基本的图像特征提取方面，YOLO3采用了Darknet-53的网络结构 (含有53个卷积层)，它借鉴了残差网络ResNet的做法，在层之间设置了shortcut，来解决深层网络梯度的问题，shortcut如下图所示: 包含两个卷积层和一个shortcut connections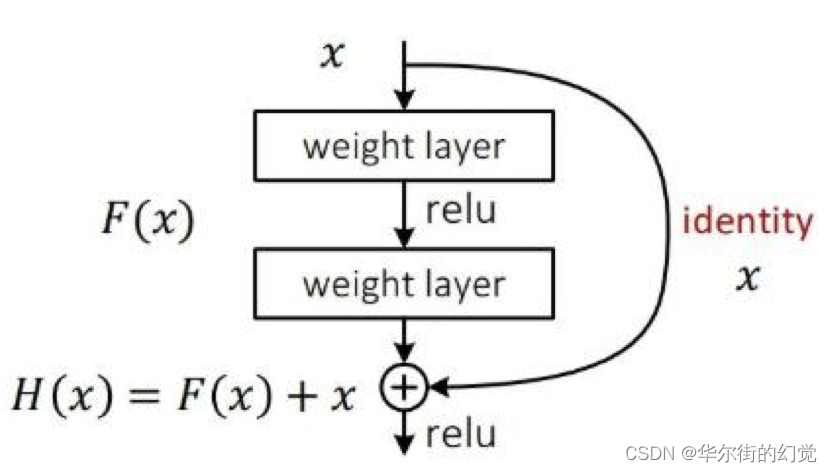
YoloV3的模型结构如下所示：
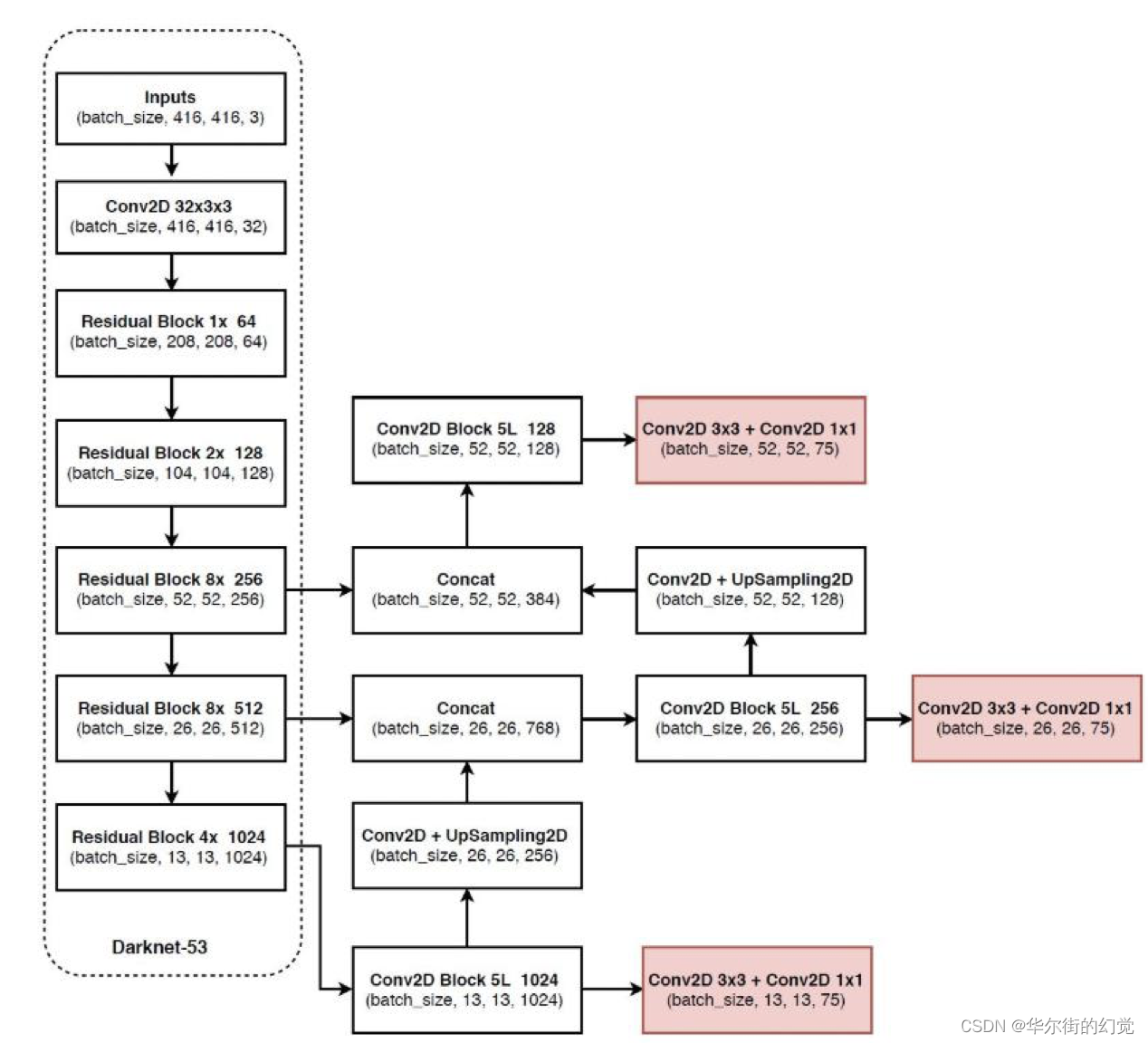
整个v3结构里面，没有池化层和全连接层，网络的下采样是通过设置卷积的stride为2来达到的，每当通过这个卷积层之后图像的尺寸就会减小到一半。残差模块中的1x，2x，8x，8x 等表示残差模块的个数。
YOLOv3的网络结构由基础特征提取网络、multi-scale特征融合层和输出层组成。
- 特征提取网络：YOLOv3使用DarkNet53作为特征提取网络:DarkNet53 基本采用了全卷积网络，用步长为2的卷积操作替代了池化层，同时添加了 Residual 单元，避免在网络层数过深时发生梯度弥散。
- 特征融合层：为了解决之前YOLO版本对小目标不敏感的问题，YOLOv3采用了3个不同尺度的特征图来进行目标检测，分别为13x13,26x26,52x52,用来检测大、中、小三种目标。特征融合层选取 DarkNet 产出的三种尺度特征图作为输入，借鉴了FPN(feature pyramid networks)的思想，通过一系列的卷积层和上采样对各尺度的特征图进行融合
- 输出层：同样使用了全卷积结构，其中最后一个卷积层的卷积核个数是255:3x(20+4+1)=75表示一个grid cell包含3个bounding box，4表示框的4个坐标信息，1表示Confidence Score，20表示VOC数据集中80个类别的概率。如果换用别的数据集，20可以更改为实际类别数量。
3.9.4 先验框
yoloV3采用K-means聚类得到先验框的尺寸，为每种尺度设定3种先验框，总共聚类出9种尺寸的先验框。
在COCO数据集这9个先验框是: (10x13)，(16x30)，(33x23)，(30x61),(62x45)，(59x119)，(116x90)，(156x198)，(373x326)。在最小的(13x13)特征图上(有最大的感受野) 应用较大的先验框(116x90)，(156x198)，(373x326)，适合检测较大的对象。中等的(26x26)特征图上 (中等感受野) 应用中等的先验框(30x61)，(62x45)，(59x119)，适合检测中等大小的对象。较大的(52x52)特征图上(较小的感受野) 应用,其中较小的先验框(10x13)，(16x30)，(33x23)，适合检测较小的对象。
直观上感受9种先验框的尺寸，下图中蓝色框为聚类得到的先验框。黄色框式ground truth，红框是对象中心点所在的网格。
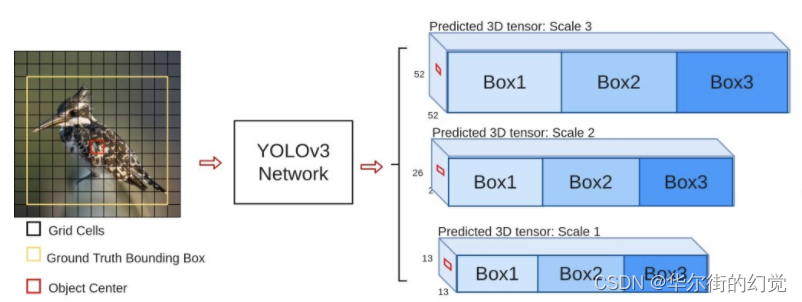
3.9.5 YoloV3模型的输⼊与输出
预测对象类别时不使用softmax，而是被替换为一个1x1的卷积层+logistic激活函数的结构。使用softmax层的时候其实已经假设每个输出仅对应某一个单个的class.但是在某些class存在重叠情况 (例如woman和person)的数据集中，使用softmax就不能使网络对数据进行很好的预测。
YoloV3的输⼊输出形式如下图所示：
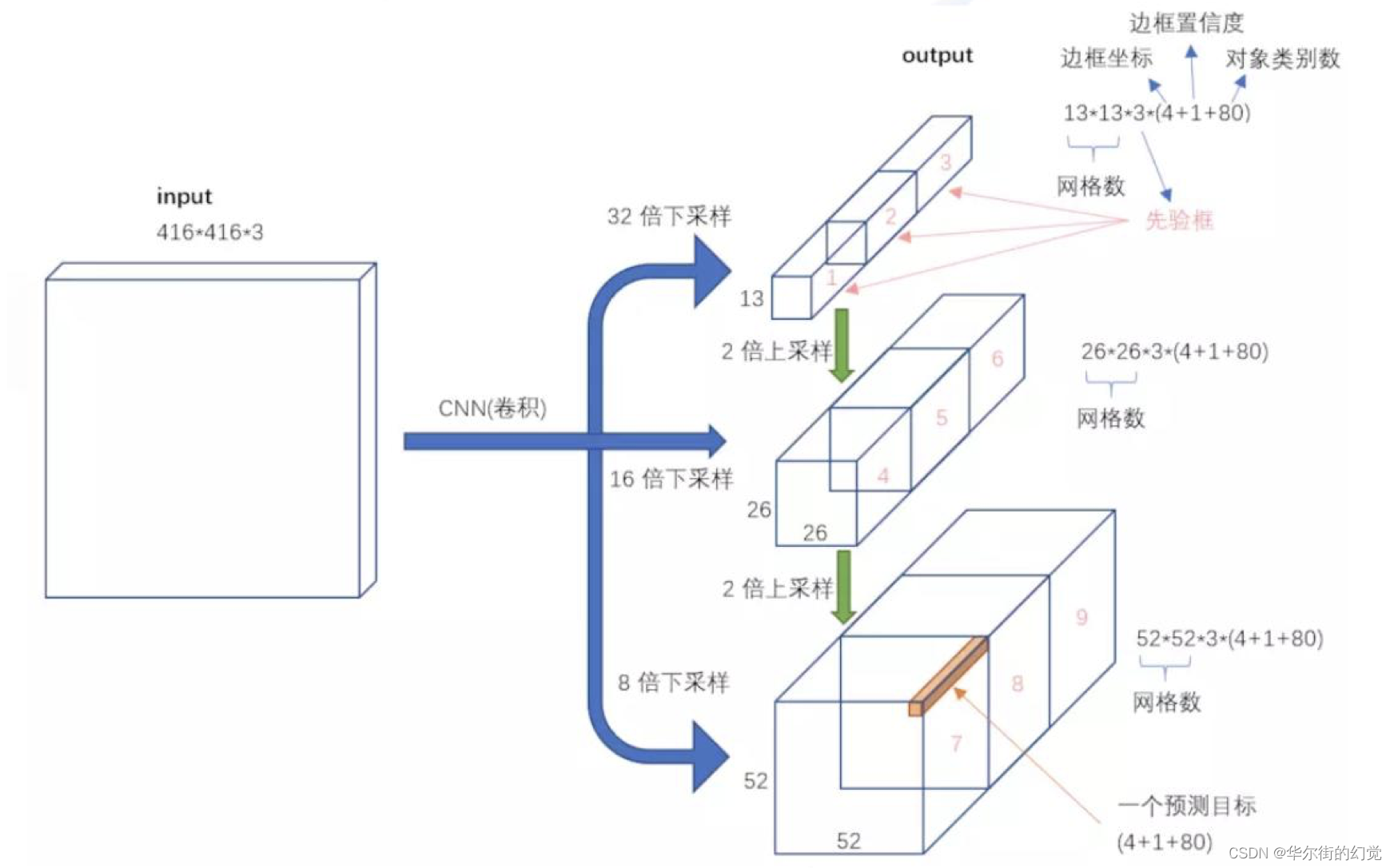
输入416x416x3的图像，通过darknet网络得到三种不同尺度的预测结果，每个尺度都对应N个通道，包含着预测的信息;
每个网格每个尺寸的anchors的预测结果。
YOLOv3共有13x13x3 + 26x26x3 + 52x52x3个预测 。每个预测对应85维，分别是4 (坐标值)、1 (置信度分数) 、80 (coco类别概率)
3.9.6 YoloV3的目标检测
在这里我们进行的目标检测是基于OPenCV的利用voloV3进行目标检测，不涉及yoloV3的模型结构、理论及训练过程，只是利用训练好的模型进行目标检测，整个流程如下:
基于OPenCV中的DNN模块
- 加载已训练好的volov3模型及其权重参数
- 将要处理的图像转换成输入到模型中的blobs
- 利用模型对目标进行检测
- 遍历检测结果
- 应用非极大值抑制
绘制最终检测结果，并存入到ndarray中，供目标追踪使用
代码如下:
-
加载yolov3模型及其权重参数
# 1.加载可以识别物体的名称，将其存放在LABELS中，⼀共有80种，在这我们只使⽤car labelsPath = "./yolo-coco/coco.names" LABELS = open(labelsPath).read().strip().split("\n") # 设置随机数种⼦，⽣成多种不同的颜⾊，当⼀个画⾯中有多个⽬标时，使⽤不同颜⾊的框将其框起来 np.random.seed(42) COLORS = np.random.randint(0, 255, size=(200, 3),dtype="uint8") # 加载已训练好的yolov3⽹络的权重和相应的配置数据 weightsPath = "./yolo-coco/yolov3.weights" configPath = "./yolo-coco/yolov3.cfg" # 加载好数据之后，开始利⽤上述数据恢复yolo神经⽹络(Darknet对应yolov3模型) net = cv2.dnn.readNetFromDarknet(configPath, weightsPath) # 获取YOLO中每⼀⽹络层的名称：['conv_0', 'bn_0', 'relu_0', 'conv_1', 'bn_1', 'relu_1','conv_2'] ln = net.getLayerNames() # 获取输出层在⽹络中的索引位置，并以列表的形式：['yolo_82', 'yolo_94', 'yolo_106'] ln = [ln[i[0] - 1] for i in net.getUnconnectedOutLayers()]- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
-
要处理的图像转换成输入到模型中的blobs
# 2. 读取图像 frame = cv2.imread("./images/car1.jpg") # 视频的宽度和⾼度，即帧尺⼨ (W, H) = (None, None) if W is None or H is None: (H, W) = frame.shape[:2] # 根据输⼊图像构造blob,利⽤OPenCV进⾏深度⽹路的计算时，⼀般将图像转换为blob形式，对图⽚进⾏预处理,包括缩放、减均值、通道变换等 # 还可以设置尺⼨，⼀般设置为在进⾏⽹络训练时的图像的⼤⼩ blob = cv2.dnn.blobFromImage(frame, 1 / 255.0, (416, 416), swapRB=True, crop=False)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
-
利⽤模型对⽬标进⾏检测
# 3.将blob输⼊到前向⽹络中，并进⾏预测 net.setInput(blob) start = time.time() # yolo前馈计算，获取边界和相应的概率 # 输出layerOutsputs介绍： # 是YOLO算法在图⽚中检测到的bbx的信息 # 由于YOLO v3有三个输出，也就是上⾯提到的['yolo_82', 'yolo_94', 'yolo_106'] # 因此layerOutsputs是⼀个⻓度为3的列表 # 其中，列表中每⼀个元素的维度是(num_detection, 85) # num_detections表示该层输出检测到bbx的个数 # 85：因为该模型在COCO数据集上训练，[5:]表示类别概率；[0:4]表示bbx的位置信息；[5]表示置信度 layerOutputs = net.forward(ln)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
-
遍历检测结果,获得检测框
# 判定每⼀个bbx的置信度是否⾜够的⾼，以及执⾏NMS算法去除冗余的bbx boxes = [] # ⽤于存放识别物体的框的信息，包括框的左上⻆横坐标x和纵坐标y以及框的⾼h和宽w confidences = [] # 表示识别⽬标是某种物体的可信度 classIDs = [] # 表示识别的⽬标归属于哪⼀类，['person', 'bicycle', 'car', 'motorbike',...] # 4. 遍历每⼀个输出层的输出 for output in layerOutputs: # 遍历某个输出层中的每⼀个⽬标 for detection in output: scores = detection[5:] # 当前⽬标属于某⼀类别的概率 classID = np.argmax(scores) # ⽬标的类别ID confidence = scores[classID] # 得到⽬标属于该类别的置信度 # 只保留置信度⼤于0.3的边界框，若图⽚质量较差，可以将置信度调低⼀点 if confidence > 0.3: # 将边界框的坐标还原⾄与原图⽚匹配，YOLO返回的是边界框的中⼼坐标以及边界框的宽度 box = detection[0:4] * np.array([W, H, W, H]) (centerX, centerY, width, height) = box.astype("int") # 使⽤ astype x = int(centerX - (width / 2)) # 计算边界框的左上⻆的横坐标 y = int(centerY - (height / 2)) # 计算边界框的左上⻆的纵坐标 # 更新检测到的⽬标框，置信度和类别ID boxes.append([x, y, int(width), int(height)]) # 将边框的信息添加到列表boxes confidences.append(float(confidence)) # 将识别出是某种物体的置信度添加到confidences classIDs.append(classID) # 将识别物体归属于哪⼀类的信息添加到列表classIDs- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
-
⾮极⼤值抑制
# 5. ⾮极⼤值抑制 idxs = cv2.dnn.NMSBoxes(boxes, confidences, 0.5, 0.3)- 1
- 2
-
最终检测结果，绘制，并存入到ndarray中，供目标追踪使用
# 6. 获得最终的检测结果 dets = [] # 存放检测框的信息，包括左上⻆横坐标，纵坐标，右下⻆横坐标，纵坐标，以及检测到的物体的置信度,用于目标跟踪 if len(idxs) > 0: # 存在检测框的话（即检测框个数⼤于0） for i in idxs.flatten(): # 循环检测出的每⼀个box # yolo模型可以识别很多⽬标，因为我们在这⾥只是识别⻋，所以只有⽬标是⻋的我们进⾏检测,其他的忽略 if LABELS[classIDs[i]] == "car": (x, y) = (boxes[i][0], boxes[i][1]) # 得到检测框的左上⻆坐标 (w, h) = (boxes[i][2], boxes[i][3]) # 得到检测框的宽和⾼ cv2.rectangle(frame, (x, y), (x+w, y+h), (0,255,0), 2) # 将⽅框绘制到画面上 dets.append([x, y, x + w, y + h, confidences[i]]) # 将检测框的信息的放入dets中 # 设置数据类型，将整型数据转换为浮点数类型，且保留⼩数点后三位 np.set_printoptions(formatter={'float': lambda x: "{0:0.3f}".format(x)}) # 将检测框数据转换为ndarray,其数据类型为浮点型 dets = np.asarray(dets) plt.imshow(frame[:,:,::-1])- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
在视频中进⾏⽬标检测：
labelsPath = "./yolo-coco/coco.names"
LABELS = open(labelsPath).read().strip().split("\n")
# 设置随机数种⼦，⽣成多种不同的颜⾊，当⼀个画⾯中有多个⽬标时，使⽤不同颜⾊的框将其框起来
np.random.seed(42)
COLORS = np.random.randint(0, 255, size=(200, 3),dtype="uint8")
# 加载已训练好的yolov3⽹络的权重和相应的配置数据
weightsPath = "./yolo-coco/yolov3.weights"
configPath = "./yolo-coco/yolov3.cfg"
# 加载好数据之后，开始利⽤上述数据恢复yolo神经⽹络
net = cv2.dnn.readNetFromDarknet(configPath, weightsPath)
# 获取YOLO中每⼀⽹络层的名称：['conv_0', 'bn_0', 'relu_0', 'conv_1', 'bn_1', 'relu_
ln = net.getLayerNames()
# 获取输出层在⽹络中的索引位置，并以列表的形式：['yolo_82', 'yolo_94', 'yolo_106']
ln = [ln[i[0] - 1] for i in net.getUnconnectedOutLayers()]
"""
视频处理类
"""
# 初始化vediocapture类，参数指定打开的视频⽂件，也可以是摄像头
vs = cv2.VideoCapture('./input/test_1.mp4')
# 视频的宽度和⾼度，即帧尺⼨
(W, H) = (None, None)
# 视频⽂件写对象
writer = None
try:
# 确定获取视频帧数的⽅式
prop = cv2.cv.CV_CAP_PROP_FRAME_COUNT if imutils.is_cv2() \
else cv2.CAP_PROP_FRAME_COUNT
# 获取视频的总帧数
total = int(vs.get(prop))
# 打印视频的帧数
print("[INFO] {} total frames in video".format(total))
except:
print("[INFO] could not determine # of frames in video")
print("[INFO] no approx. completion time can be provided")
total = -1
# 循环读取视频中的每⼀帧画⾯
while True:
# 读取帧：grabbed是bool,表示是否成功捕获帧，frame是捕获的帧
(grabbed, frame) = vs.read()
# 若未捕获帧，则退出循环
if not grabbed:
break
# 若W和H为空，则将第⼀帧画⾯的⼤⼩赋值给他
if W is None or H is None:
(H, W) = frame.shape[:2]
# 根据输⼊图像构造blob,利⽤OPenCV进⾏深度⽹路的计算时，⼀般将图像转换为blob形式，对图⽚
# 还可以设置尺⼨，⼀般设置为在进⾏⽹络训练时的图像的⼤⼩
blob = cv2.dnn.blobFromImage(frame, 1 / 255.0, (416, 416), swapRB=True, crop=False)
# 将blob输⼊到前向⽹络中
net.setInput(blob)
start = time.time()
# yolo前馈计算，获取边界和相应的概率
layerOutputs = net.forward(ln)
"""
输出layerOutsputs介绍：
是YOLO算法在图⽚中检测到的bbx的信息
由于YOLO v3有三个输出，也就是上⾯提到的['yolo_82', 'yolo_94', 'yolo_106']
因此layerOutsputs是⼀个⻓度为3的列表
其中，列表中每⼀个元素的维度是(num_detection, 85)
num_detections表示该层输出检测到bbx的个数
85：因为该模型在COCO数据集上训练，[5:]表示类别概率；[0:4]表示bbx的位置信息；[5]表示置
"""
end = time.time()
"""
下⾯对⽹络输出的bbx进⾏检查：
判定每⼀个bbx的置信度是否⾜够的⾼，以及执⾏NMS算法去除冗余的bbx
"""
boxes = [] # ⽤于存放识别物体的框的信息，包括框的左上⻆横坐标x和纵坐标y以及框的⾼h和宽
confidences = [] # 表示识别⽬标是某种物体的可信度
classIDs = [] # 表示识别的⽬标归属于哪⼀类，['person', 'bicycle', 'car', 'moto
# 遍历每⼀个输出层的输出
for output in layerOutputs:
# 遍历某个输出层中的每⼀个⽬标
for detection in output:
scores = detection[5:] # 当前⽬标属于某⼀类别的概率
"""
# scores = detection[5:] ---> [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
# 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
# 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0
# 0. 0. 0. 0. 0. 0. 0. 0.]
# scores的⼤⼩应该是1*80，因为在训练yolo模型时是80类⽬标
"""
classID = np.argmax(scores) # ⽬标的类别ID
confidence = scores[classID] # 得到⽬标属于该类别的置信度
# 只保留置信度⼤于0.3的边界框，若图⽚质量较差，可以将置信度调低⼀点
if confidence > 0.3:
# 将边界框的坐标还原⾄与原图⽚匹配，YOLO返回的是边界框的中⼼坐标以及边界框的宽度和高度
box = detection[0:4] * np.array([W, H, W, H])
(centerX, centerY, width, height) = box.astype("int") # 使⽤ astype("int")对上述
x = int(centerX - (width / 2)) # 计算边界框的左上⻆的横坐标
y = int(centerY - (height / 2)) # 计算边界框的左上⻆的纵坐标
# 更新检测到的⽬标框，置信度和类别ID
boxes.append([x, y, int(width), int(height)]) # 将边框的信息添加
confidences.append(float(confidence)) # 将识别出是某种物体的置信度
classIDs.append(classID) # 将识别物体归属于哪⼀类的信息添加到列表class
# 上⼀步中已经得到yolo的检测框，但其中会存在冗余的bbox,即⼀个⽬标对应多个检测框，所以使
# 利⽤OpenCV内置的NMS DNN模块实现即可实现⾮最⼤值抑制 ，所需要的参数是边界 框、 置信度
# 第⼀个参数是存放边界框的列表，第⼆个参数是存放置信度的列表，第三个参数是⾃⼰设置的置信度
# 返回的idxs是⼀个⼀维数组，数组中的元素是保留下来的检测框boxes的索引位置
idxs = cv2.dnn.NMSBoxes(boxes, confidences, 0.5, 0.3)
dets = [] # 存放检测框的信息，包括左上⻆横坐标，纵坐标，右下⻆横坐标，纵坐标，以及检测
if len(idxs) > 0: # 存在检测框的话（即检测框个数⼤于0）
for i in idxs.flatten(): # 循环检测出的每⼀个box
# yolo模型可以识别很多⽬标，因为我们在这⾥只是识别⻋，所以只有⽬标是⻋的我们进⾏
if LABELS[classIDs[i]] == "car":
(x, y) = (boxes[i][0], boxes[i][1]) # 得到检测框的左上⻆坐标
(w, h) = (boxes[i][2], boxes[i][3]) # 得到检测框的宽和⾼
dets.append([x, y, x + w, y + h, confidences[i]]) # 将检测框的信息放入dets中
# 设置数据类型，将整型数据转换为浮点数类型，且保留⼩数点后三位
np.set_printoptions(formatter={'float': lambda x: "{0:0.3f}".format(x)})
# 将检测框数据转换为ndarray,其数据类型为浮点型
dets = np.asarray(dets)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
3.9.7 总结
-
yoloV3的多尺度检测方法
在YOLOv3中采用FPN结构来提高对应多尺度目标检测的精度，当前的feature map利用“未来”层的信息，将低阶特征与高阶特征进行融合，提升检测精度。 -
yoloV3模型的网络结构
以darknet-53为基础，借鉴resnet的思想，在网络中加入了残差模块，利于解决深层次网络的梯度问题
整个v3结构里面，没有池化层和全连接层，只有卷积层
网络的下采样是通过设置卷积的stride为2来达到的 -
yoloV3模型先验框设计的方法
采用K-means聚类得到先验框的尺寸，为每种尺度设定3种先验框，总共聚类出9种尺寸的先验框。 -
yoloV3模型为什么适用于多标签的目标分类
因为预测对象类别时不使用softmax，而是使用logistic的输出进行预测 -
yoloV3模型的输入输出
对于416x416x3的输入图像，在每个尺度的特征图的每个网格设置3个先验框，总共有13x13x3 +26x26x3 + 52x52x3= 10647 个预测。每一个预测是一个(4+1+80)=85维向量，这个85维向量包含边框坐标 (4个数值)，边框置信度 (1个数值)，对象类别的概率 (对于COCO数据集，有80种对象) -
基于OPenCV的DNN模块利用yoloV3模型进行目标检测
- 加载已训练好的yolov3模型及其权重参数
- 将要处理的图像转换成输入到模型中的blobs
- 利用模型对目标进行检测
- 遍历检测结果，应用非极大值抑制
- 绘制最终检测结果，并存入到ndarray中，供目标追踪使用。
3.10 车流量统计
学习目标
- 了解车流量统计的方法
- 实现车流量检测
3.10.1 基于虚拟线圈法的车辆统计
基于虚拟线圈的车流量统计算法原理与交通道路上的常见的传统的物理线圈类似由于物理线圈需要埋设在路面之下，因此会有安装、维护费用高，造成路面破坏等问题，而采用基于视频的虚拟线圈的车辆计数方法完全避免了以上问题，且可以针对多个感兴趣区域进行检测。
虚拟线圈车辆计数法的原理是在采集到的交通流视频中，在需要进行车辆计数的道路或路段上设置一条或一条以上的检测线对通过车辆进行检测，从而完成计数工作。检测线的设置原则一般是在检测车道上设置一条垂直于车道线，居中的虚拟线段，通过判断其与通过车辆的相对位置的变化，完成车流量统计的工作。如下图所示，绿色的线就是虚拟检测线:
在该项目中我们进行检测的方法是，计算前后两帧图像的车辆检测框的中心点连线，若该连线与检测线相交，则计数加一，否则计数不变。那怎么判断两条线段是否相交呢?
假设有两条线段AB，CD，若AB，CD相交，我们可以确定
1.线段AB与CD所在的直线相交，即点A和点B分别在直线CD的两边
2.线段CD与AB所在的直线相交，即点C和点D分别在直线AB的两边
上面两个条件同时满足是两线段相交的充要条件，所以我们只需要证明点A和点B分别在直线CD的两边，点C和点D分别在直线AB的两边，这样便可以证明线段AB与CD相交了。
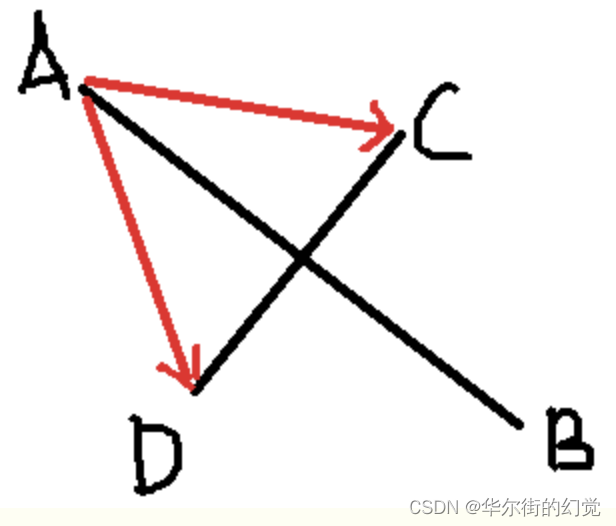
在上图中，线段AB与线段CD相交，于是我们可以得到两个向量AC，AD，C和D分别在AB的两边，向量AC在向量AB的逆时针方向，ABxAC > 0;向量AD在向量AB的顺时针方向，ABxAD < 0，两叉乘结果异号。
这样，方法就出来了：如果线段CD的两个端点C和D，与另一条线段的一个端点(A或B，只能是其中一个) 连成的向量，与向量AB做叉乘，若结果异号，表示C和D分别在直线AB的两边，若结果同号，则表示CD两点都在AB的一边，则肯定不相交。
所以我们利用叉乘的方法来判断车辆是否经过检测线
3.10.2 实现
实现车流量检测的代码如下
-
检测AB和CD两条直线是否相交
# 计算有A，B，C三点构成的向量CA，BA之间的关系， def ccw(A, B, C): return (C[1] - A[1]) * (B[0] - A[0]) > (B[1] - A[1]) * (C[0] - A[0]) # 检测AB和CD两条直线是否相交 def intersect(A, B, C, D): return ccw(A, C, D) != ccw(B, C, D) and ccw(A, B, C) != ccw(A, B, D)- 1
- 2
- 3
- 4
- 5
- 6
- 7
遍历跟踪框判断其与检测线是否相交，并进行车辆计数
# 基准线
line = [(8,150),(2560,158)]
# 车辆总数
counter = 0
#正向车道的车辆数据
counter_up = 0
#逆向车道的车辆数据
counter_down = 0
if len(boxes) > 0:
i = int(0)
# 遍历跟踪框
for box in boxes:
(x, y) = (int(box[0]), int(box[1])) # 计算跟踪框的左上⻆坐标
(w, h) = (int(box[2]), int(box[3])) # 计算跟踪框的宽和⾼
color = [int(c) for c in COLORS[indexIDs[i] % len(COLORS)]] # 对⽅框的颜⾊进
cv2.rectangle(frame, (x, y), (w, h), color, 2) # 将⽅框绘制在画⾯上
"""
根据当前帧的检测结果，与上⼀帧检测的检测结过，进⾏虚拟线圈完成⻋辆计数：⻋流量统计
"""
if indexIDs[i] in previous:
previous_box = previous[indexIDs[i]] # 获取上⼀帧识别的⽬标框
(x2, y2) = (int(previous_box[0]), int(previous_box[1])) # 获取上⼀帧画⾯的左上角坐标
(w2, h2) = (int(previous_box[2]), int(previous_box[3])) # 获取上⼀帧画⾯的宽和高
p0 = (int(x + (w - x) / 2), int(y + (h - y) / 2)) # 获取当前帧检测框的中⼼点
p1 = (int(x2 + (w2 - x2) / 2), int(y2 + (h2 - y2) / 2)) # 获取上⼀帧检测框的中心点
cv2.line(frame, p0, p1, color, 3) # 将前后两帧图像的检测结果中⼼连接起来
"""
进⾏碰撞检测-前后两帧检测框中⼼点的连线穿过基准线，则进⾏计数
:param line:基准线
:param p0-p1:构成的线
"""
if intersect(p0, p1, line[0], line[1]):
# 总计数加1
counter += 1
# 判断⾏进的⽅向
if y2 < y:
counter_down += 1 # 逆向⾏驶+1
else:
counter_up += 1 # 正向⾏驶+1
i += 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
总结
- 基于虚拟线圈的目标检测，是设置一个垂直于车道的检测线，判断跟踪车辆与检测线之间的关系，完成车辆计数
- 利用叉乘的方法来检验车辆是否与检测线相交
3.11 视频中的车流量统计
学习目标
- 了解视频中处理车流量统计的方法
前面我们已经完成了视频中车辆的检测功能，下面我们对车辆进行跟踪，并将跟踪结果绘制在视频中
主要分为以下步骤:
- 对目标进行追踪
- 绘制车辆计数结果
- 将检测结果绘制在视频中并进行保存
-
对目标进行追踪
# yolo中检测结果为0时，传⼊跟踪器中会出现错误，在这⾥判断下，未检测到⽬标时不进⾏⽬标追踪 if np.size(dets) == 0: continue else: tracks = tracker.update(dets) # 将检测结果传⼊跟踪器中，返回当前画⾯中跟踪成功,包含5个信息 # 对跟踪器返回的结果进⾏处理 boxes = [] # 存放tracks中的前四个值：⽬标框的左上⻆横纵坐标和右下⻆的横纵坐标 indexIDs = [] # 存放tracks中的最后⼀个值：置信度，⽤来作为memory中跟踪框的Key previous = memory.copy() # ⽤于存放上⼀帧的跟踪结果，⽤于碰撞检测 memory = {} # 存放当前帧⽬标的跟踪结果，⽤于碰撞检测 # 遍历跟踪结果，对参数进⾏更新 for track in tracks: boxes.append([track[0], track[1], track[2], track[3]]) # 更新⽬标框坐标信 indexIDs.append(int(track[4])) # 更新置信度信息 memory[indexIDs[-1]] = boxes[-1] # 将跟踪框以key为：置信度，value为：跟踪框坐标形式存入memory中- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
-
绘制⻋辆计数结果
# 绘制⻋辆计数的相关信息 cv2.line(frame, line[0], line[1], (0, 255, 0), 3) # 根据设置的基准线将其绘制在画⾯ cv2.putText(frame, str(counter), (30, 80), cv2.FONT_HERSHEY_DUPLEX, 3.0, (255,0,0), 3) # 绘制车辆总计数 cv2.putText(frame, str(counter_up), (130, 80), cv2.FONT_HERSHEY_DUPLEX, 3.0, (0,255,0), 3) # 绘制车辆正向⾏驶 cv2.putText(frame, str(counter_down), (230, 80), cv2.FONT_HERSHEY_DUPLEX, 3.0, (0,0,255), 3)# 绘制车辆逆向⾏驶- 1
- 2
- 3
- 4
- 5
-
将结果保存在视频中
# 未设置视频的编解码信息时，执⾏以下代码 if writer is None: # 设置编码格式 fourcc = cv2.VideoWriter_fourcc(*"mp4v") # 视频信息设置 writer = cv2.VideoWriter("./output/output.mp4",fourcc,30,(frame.shape[1], frame.shape[0]),True) # 将处理后的帧写⼊到视频中 writer.write(frame) # 显示当前帧的结果 cv2.imshow("", frame) # 按下q键退出 if cv2.waitKey(1) & 0xFF == ord('q'): break- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
总结
- 对目标进行追踪
- 绘制车辆计数的相关信息
- 将结果保存在视频中
4 车道线检测
项目简介
汽车的日益普及在给人们带来极大便利的同时，也导致了拥堵的交通路况，以及更为频发的交通事故。而自动驾驶技术的出现可以有效的缓解了此类问题，减少交通事故，提升出行效率。自动驾驶的首要任务就是准确的识别出车道线并根据车道线的指示进行行驶。
国内外检测车道线的方法主要有两类：一类是基于模型的检测方法，还有一类是基于特征的检测方法
- 基于模型的检测方法是将车道赋予一种合适的数学模型，并基于该模型对车道线进行拟合。
- 原理就是在结构化的道路上根据车道线的几何特征为车道线匹配合适的曲线模型，在采用最小二乘法，Hough变换等方法对车道线进行拟合
- 常用的数学模型有直线型、抛物线模型以及样条曲线模型。这种方法对噪0声抗干扰能力强。但也存在弊端，即一种车道线模型不能同时适应多种道路场景。
- 基于特征的检测方法是根据车道线自身的特征信息，通过边缘检测或者闽值分割将车道线的特征信息从路面区域中提取出来。
- 该方法对车道线的边缘特征要求较高，在边缘特征明显的情况下可获得较9好的结果，但对噪声很敏感，鲁棒性较差。
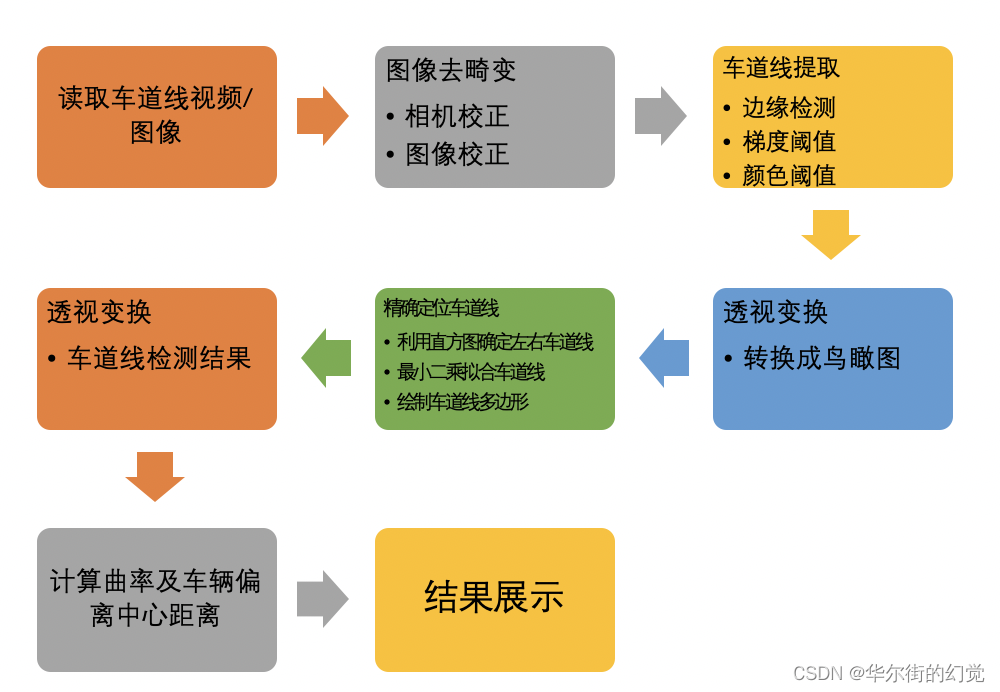
本项目针对车载相机获得的道路图像进行提取
- 首先对图像进行校正
- 利用边缘提取和颜色阈值的方法提取车道线
- 利用透视变换将图像转换为鸟瞰图
- 利用直方图统计的方法确定左右车道位置
- 并利用最小二乘法拟合车道线，并利用透视变换将检测结果绘制在图像上
- 最后计算车道线的曲率及车辆偏离车道中央的距离
流程如下图示:
4.1 相机校正
学习目标
- 了解相机的成像原理
- 了解相机标定的分类，原理和意义
- 了解图像畸变
- 知道相机标定过程中的坐标系
- 知道张氏标定法的原理及实现
- 了解双目校正
4.1.1 相机标定的意义
我们所处的世界是三维的，而照片是二维的，我们可以把相机认为是一个函数，输入量是一个场景，输出量是一幅灰度图。这个从三维到二维的过程的函数是不可逆的。
相机标定的⼀个⽬的是要找⼀个合适的数学模型，求出这个模型的参数，能够近似从三维到⼆维的过程，使这个三维到⼆维的过程的函数找到反函数。
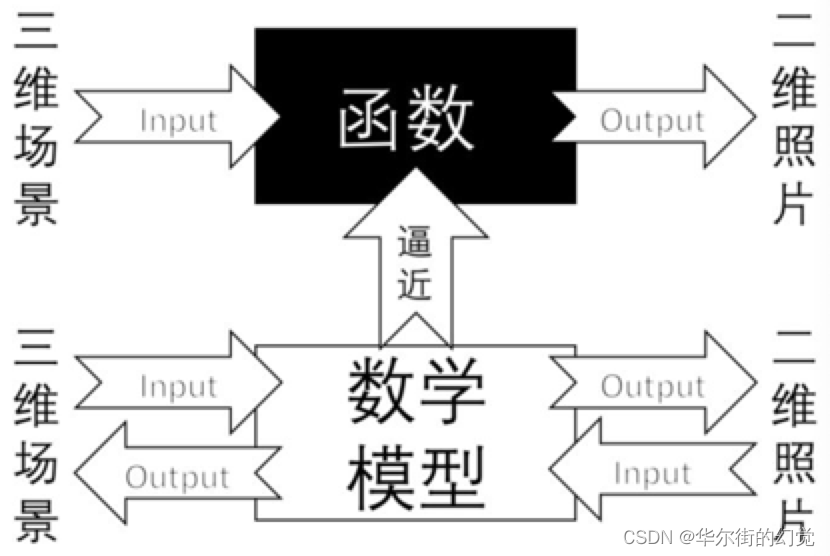
这个逼近的过程就是相机标定，我们⽤简单的数学模型来表达复杂的成像过程。
由此可知，相机标定的一个目的就是建立像素坐标系和世界坐标系之间的关系。原理是根据摄像机的模型，由已知特征点的图像坐标求解摄像机的模型参数，并求出成像的反过程，从而从图像中恢复出空间点的三维坐标，达到三维重建的目的。
另外相机标定还可以进行图像校正，由于透镜的制造精度以及组装工艺的偏差会引入畸变，导致图形失真，所以我们可以求解畸变参数，对图像进行去畸变。
4.1.2 成像原理
在介绍相机标定之前，我们首先来看下相机的成像模型。也就是，现实物体上的个点在相机采集到的图像中所在的位置是怎么确定的。我们采用的模型是针孔模型，也就是小孔成像。
小孔成像是利用了光线直线传播的原理。比如说，远处有一棵大树，而我们有个盒子，在这个盒子的对着大树的那一面上用针尖戳一个小孔。我们任选这棵大树上的任何的一个点，它都会向四周去反射无数条光线。但是因为光线是直线传播的，所以这些光线要么没有一条能进入盒子中，要么就只有一条光线是进入到这个盒子里面的。进入到盒子中的光线会在盒子里的一面上形成一个光点。这个光点跟大树上的某个点是对应的，颜色也是一致的，这就建立了一对一的关系。如果我们把感光胶片或者感光的传感器放在盒子里，就可以做成一个针孔相机来得到大树的彩色图像了。如下图所示：
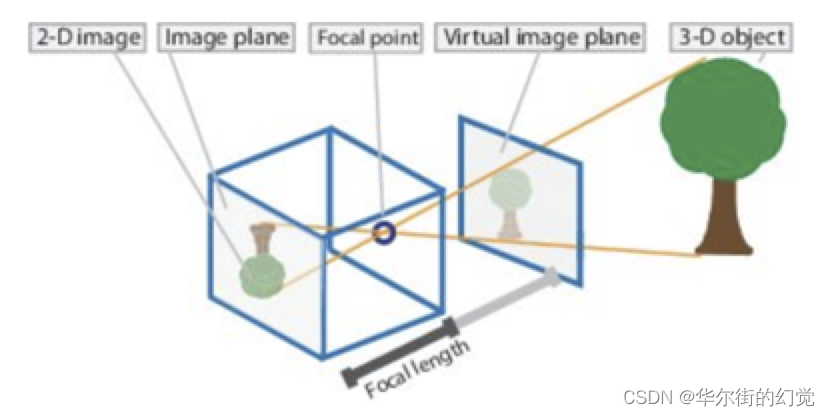
由于大树上每个点反射的无数条光线只有一条进入到盒子中，所以图像是很暗的。而加大孔径，虽然可以提高图像的亮度，却会使物体上的某一个点会反射一小束光进入到相机里。这一小束光会在感光传感器上形成一个光斑，而不是一个点;从而相机失去了物体与图像上的点的一一对应关系，进而导致图像模糊甚至无法成像。当然实际的针孔相机不可能是让每个点只有一条光线进入相机。因为光具有波粒二象性，是可以衍射的，所以很小的针孔，也会导致图像模糊。根据可见光的波长理论计算的小孔最佳直径是 0.25mm 左右，相应的光圈值大概是 f/200
所以用一个直径比针孔直径大许多的凸透镜来替代针孔。凸透镜可以把物体上的一个点所反射的那一小束通过透镜的光重新汇聚成一个点，这样，不但图像亮度增大了，而且物体和图像上点的又可以一一对应起来了。这就是我们现在常用的相机的基本工作原理。
4.1.3 相机成像模型
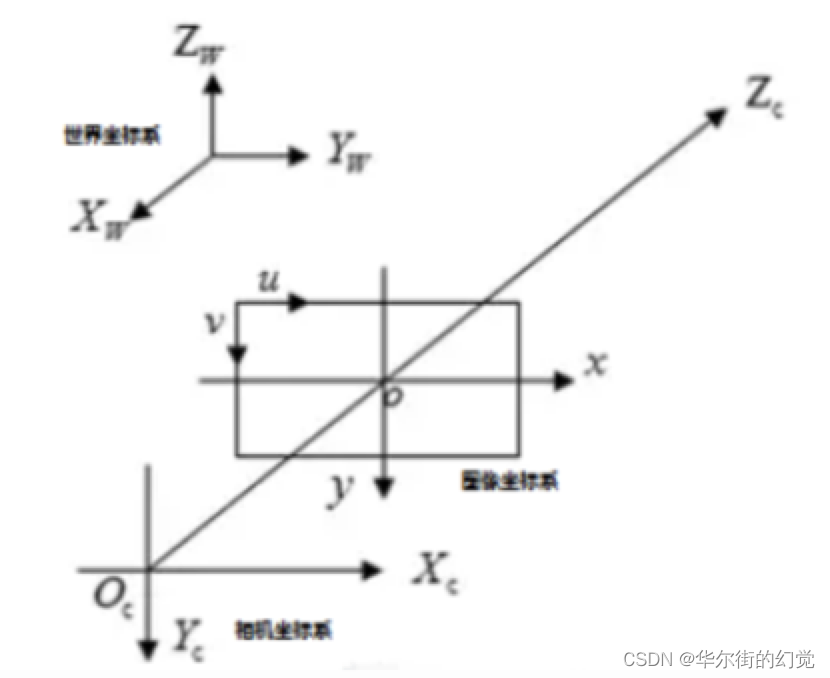
- 世界坐标系(Xw,Yw,Zw)：是目标物体位置的参考系，是为了更好的描述相机的位置创建的，世界坐标系可以根据运算方便自由放置。单位为长度单位，比如说m。在双目视觉中世界坐标系主要有三个用途:
- 标定时确定标定物的位置;
- 作为双目视觉的系统参考系，给出两个摄像机相对世界坐标系的关系，从而求出相机之间的相对关系;
- 作为重建得到三维坐标的容器，存放重建后的物体的三维坐标。世界坐标系是将看见中物体纳入运算的第一站。
- 相机坐标系(XC,YC,ZC)：是相机站在自己的角度衡量物体的坐标系。相机坐标系以相机的光心(凸透镜的中心点) 为原点，z轴与摄像机的光轴平行。拍摄的物体需要在世界坐标系下，转换为经历刚体变化转到摄像机坐标系，然后在和图像坐标系发生关系。它是图像坐标与世界坐标之间发生关系的纽带，沟通了世界上最远的距离。单位为长度单位，如mm。
- 图像坐标系(x,y)：以图像平面的中心为坐标原点，为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标。图像坐标系是用物理单位(例如毫米)表示像素在图像中的位置。
- 像素坐标系(u,v)：以图像平面的左上角顶点为原点，为了描述物体成像后的像点在数字图像上的坐标而引入，是我们真正从相机内读取到的信息所在的坐标系。像素坐标系就是以像素为单位的图像坐标系
注意:也有很多人把图像坐标系和像素坐标系合在一起，称作三大坐标系，也有人分开，称为四大坐标系。
下面我们进行一系列的变换，引入多个参数矩阵，实现从世界坐标系到像素坐标的转换。已知一个现实世界中的物体点的在世界坐标系中的坐标为 (Xw,Yw,Zw)经过相机拍摄得到图片，在图片上的像素坐标为(u,v)。假设在图像坐标系中的坐标为(x,y)，在相机坐标系中的坐标为 (Xc,Yc,Zc)。各个坐标之间的转化流程如下图所示: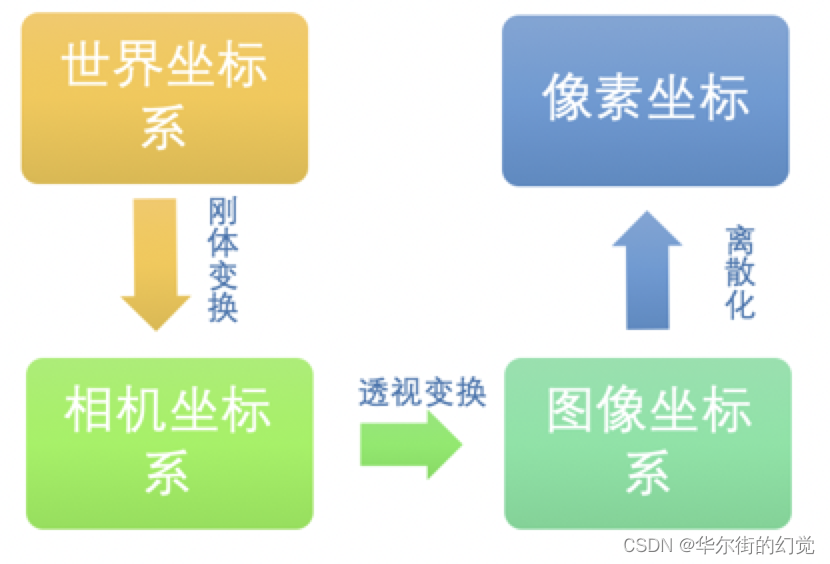
世界坐标系转换到相机坐标系时不会产生形变，所以将世界坐标系进行刚体变换就可转换为相机坐标系。三维空间中，当物体不发生形变时，而只进行旋转平移的运动，就是刚体变换。空间中的一个坐标系总可以通过刚体变换，即平移和旋转，就可以转换为另一个坐标系，如下图所示:
4.1.3.1 世界坐标系与相机坐标系之间的转换
世界坐标系转换到相机坐标系时不会产生形变，所以将世界坐标系进行刚体变换就可转换为相机坐标系。三维空间中，当物体不发生形变时，而只进行旋转平移的运动，就是刚体变换。空间中的一个坐标系总可以通过刚体变换，即平移和旋转，就可以转换为另一个坐标系，如下图所示
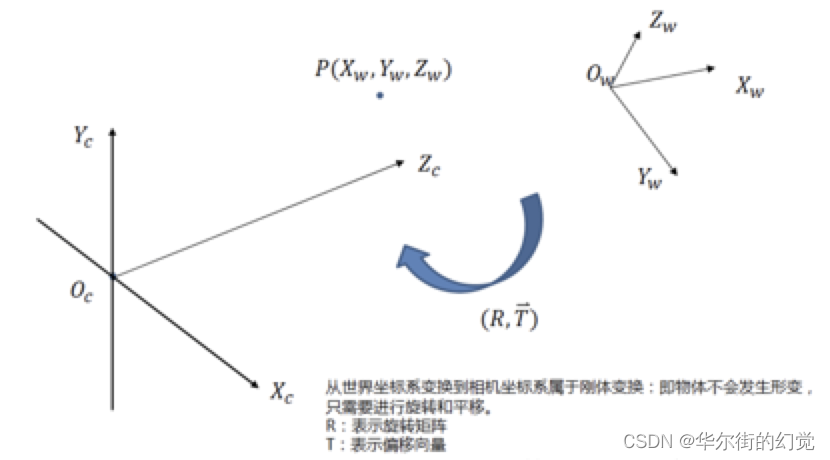两个坐标系间刚体变换的数学表达式如下所示：
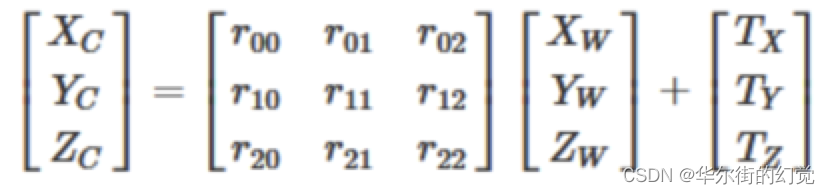可以将其写为⻬次坐标的形式：
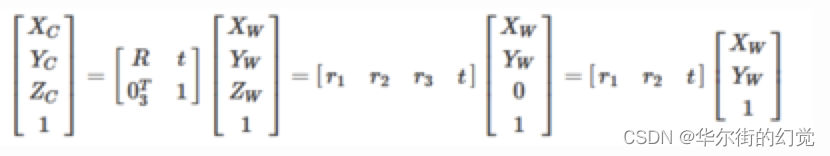
其中:XC代表摄像机坐标系，Xw代表世界坐标系。R是3*3的正交单位矩阵(即旋转矩阵，r1/r2/r3表示在x/y/z轴是旋转矩阵)，t为平移矩阵，表示可以理解为两个坐标原点之间的距离。R、与摄像机无关，所以这两个参数为摄像机的外参数(extrinsic parameter)。一般情况下，我们假定在世界坐标系中物点所在平面过世界坐标系原点且与Zw轴垂直 (也即图像平面与Xw-Yw平面重合，目的在于方便后续计算)，则Zw=0.
下面我们看下旋转矩阵的计算，现在假设坐标系沿着Z轴旋转，如下图所示:
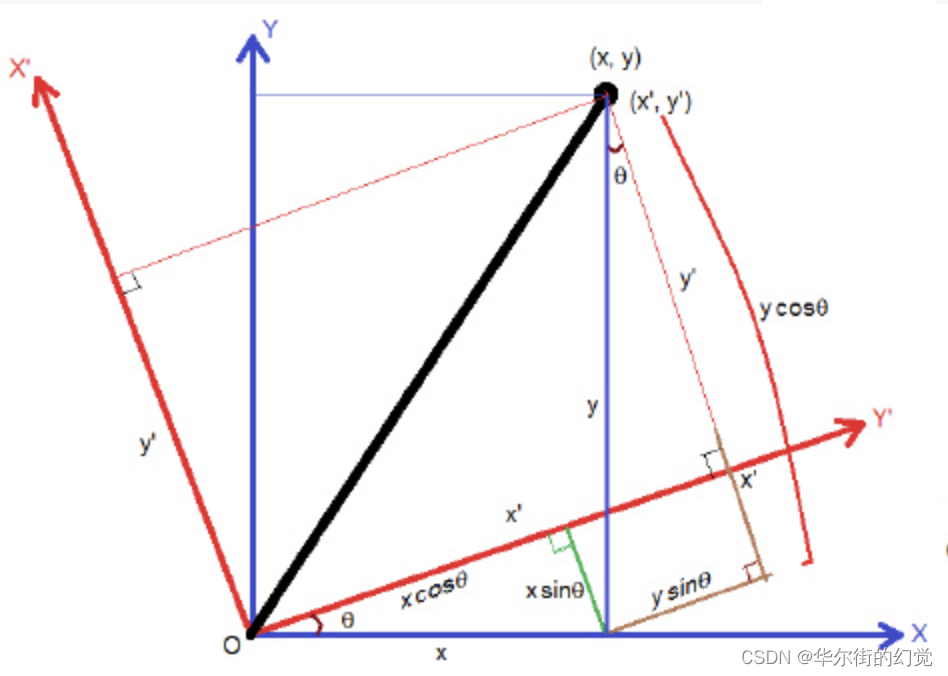则有：（假设其中x’，y’表示世界坐标系，x,y是相机坐标系）
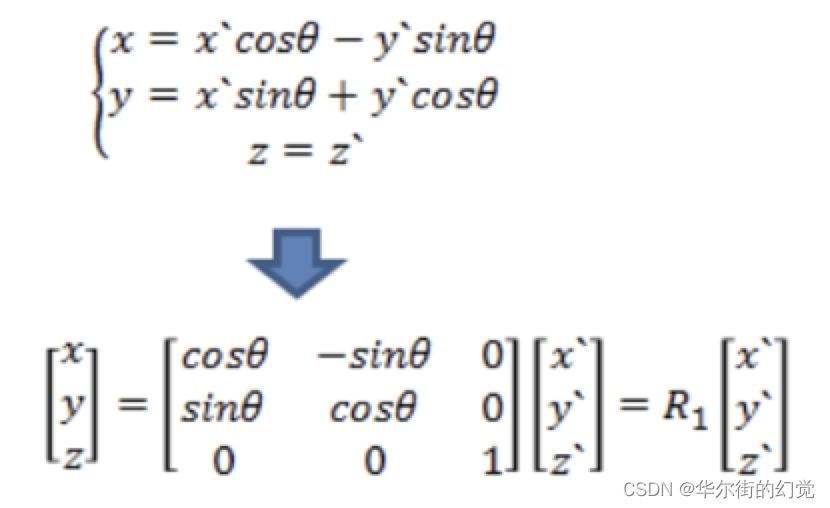同理，绕x，y轴旋转⻆度φ时，则有：
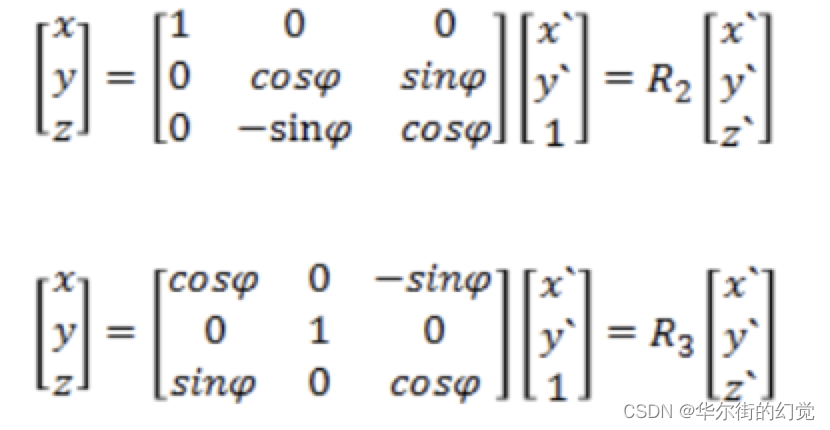所以旋转矩阵：
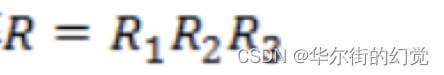
因为R受x,y,z三个⽅向上的分量的控制，所以具有三个⾃由度。
4.1.3.2 相机坐标系到图像坐标系的转换
从相机坐标系到图像坐标系，是从3d到2d的过程，属于透射投影关系：
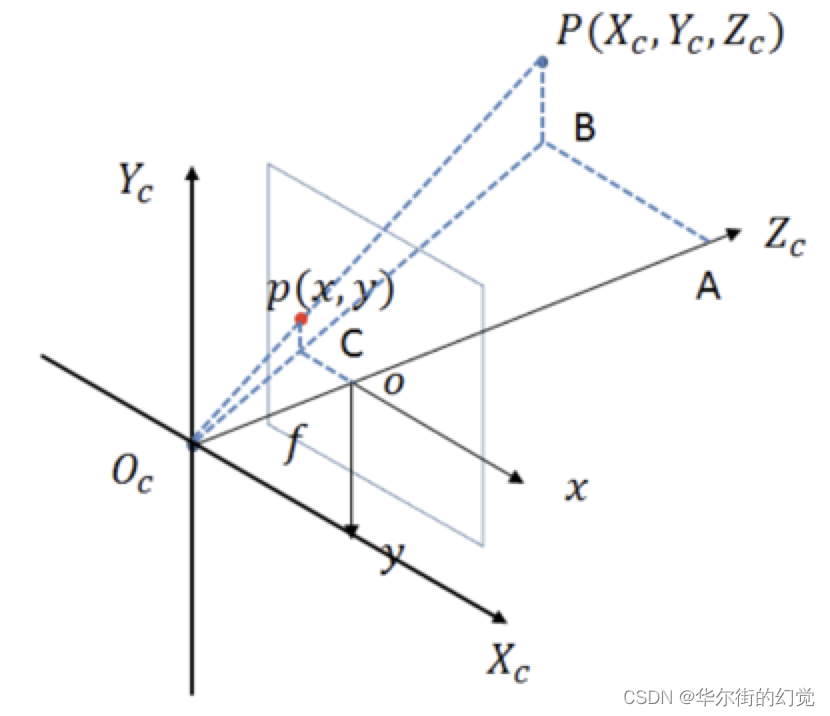如上图所示，图像坐标系为o-xy，摄像机坐标系为Oc-xcyczc。记空间点P在相机坐标系中的坐标为（Xc, Yc, Zc），在图像中的坐标是（x,y）,根据三⻆形相似定理 有：
我们把上式写成矩阵形式，并使⽤⻬次坐标，则有：
由于⻬次坐标的伸缩不变性，z [x, y, 1]T 和(x, y, 1)T 表示的是同⼀点。
4.1.3.3 图像坐标系到像素坐标系
像素坐标系和图像坐标系都在成像平⾯上，只是各⾃的原点和度量单位不⼀样。图像坐标系的原点为相机光轴与成像平⾯的交点，通常情况下是成像平⾯的中点。图像坐标系的单位是mm，属于物理单位，⽽像素坐标系的原点在图像的左上⻆，单位是pixel，也就是我们说的⼏⾏⼏列。如下图所示： 
所以这⼆者之间的转换如下：
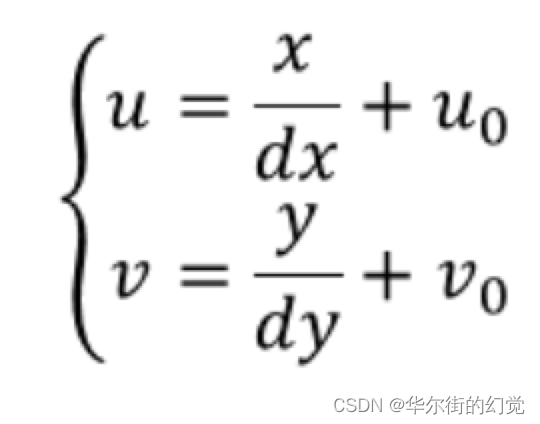
其中dx和dy表示每⼀列和每⼀⾏分别代表多少mm，即1pixel=dx mm。我们将其⽤⻬次坐标表示，并写成矩阵形式：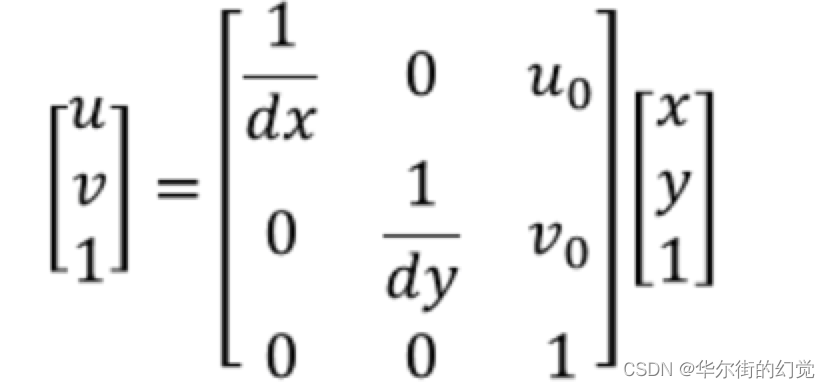
4.1.3.4 总结
我们已经介绍了各个坐标系之间的转换过程，但是我们想知道的是如何从世界坐标系转换到像素坐标系，因此我们需要把上⾯介绍到的联系起来，将三者相乘，可以把这三个过程和在⼀起，写成⼀个矩阵:
我们假设转换矩阵为P，则有：
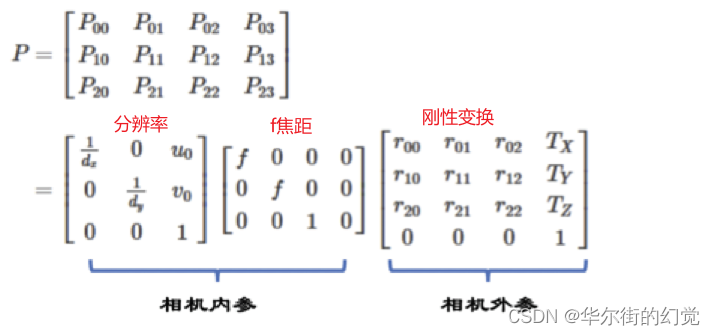
内参：（相机坐标 到 图像坐标 到像素坐标的相关参数）确定相机从三维空间到⼆维图像的投影关系，畸变系数也属于内参，我们在下⾯进⾏介绍。
外参：（世界坐标 到 相机坐标 的参数）决定相机坐标与世界坐标系之间相对位置关系，主要包括旋转和平移两部分。
4.1.4 图像畸变
我们在相机坐标系到图像坐标系变换时谈到透视投影。相机拍照时通过透镜把实物投影到像平面上，但是透镜由于制造精度以及组装工艺的偏差会引入畸变，导致原始图像的失真。因此我们需要考虑成像畸变的问题。透镜的畸变主要分为径向畸变和切向畸变两类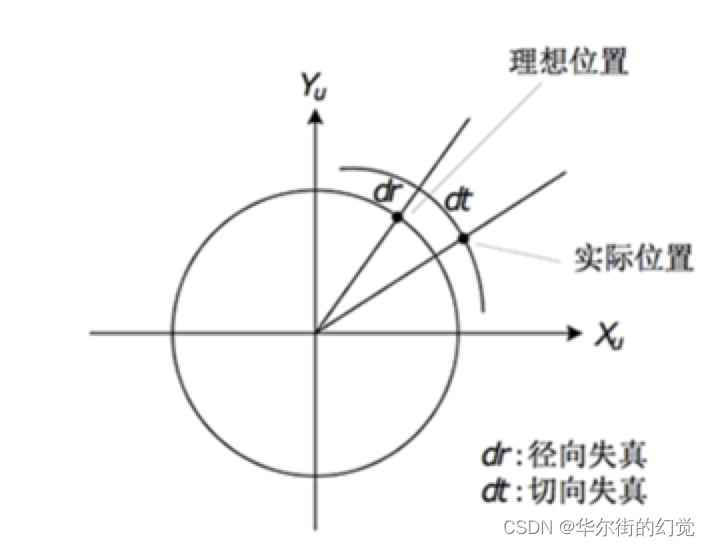
4.1.4.1 径向畸变（更多考虑）
顾名思义，径向畸变就是沿着透镜半径方向分布的畸变，产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲，这种畸变在普通的镜头中表现更加明显，径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图:(从左到右依次是:正常无畸变，桶形畸变和枕形畸变)
从上图中可以看出，径向畸变以某一个中心往外延伸，且越往外，畸变越大;显然畸变与距离成一种非线性的变换关系，可以用多项式来近似。径向畸变的数学模型可以用主点(principle point)周围的泰勒级数展开式的前几项进行描述，通常使用前两项，即k1和k2，对于畸变很大的镜头，如鱼眼镜头，可以增加使用第三项k3来进行描述，成像仪上某点根据其在径向方向上的分布位置，调节公式为:
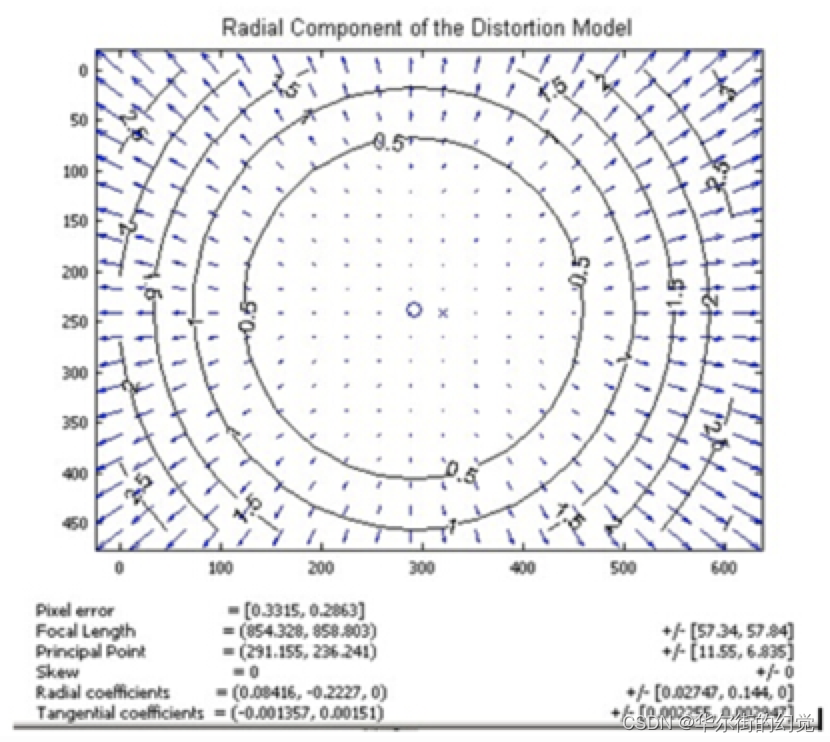
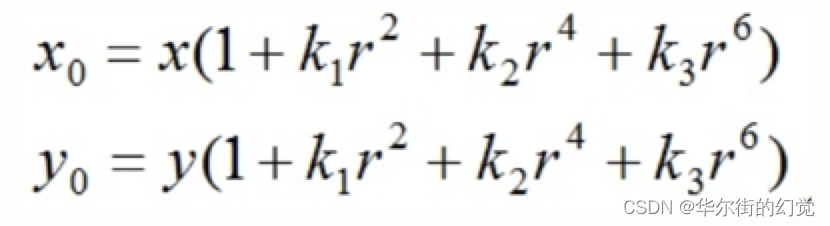式里(x0，y0)是畸变点在像平面的原始位置， (x,y)是畸变较正后新的位置下图是距离光心不同距离上的点经过透镜径向畸变后点位的偏移示意图，可以看到，距离光心越远，径向位移越大，表示畸变也越大，在光心附近，几乎没有偏移
4.1.4.2 切向畸变
切向畸变是由于透镜本身与相机传感器平面(像平面)或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。在相机传感器和镜头不平行的情况下，因为存在夹角，所以光透过镜头传到图像传感器上时，成像位置发生了变化，如下图所示：
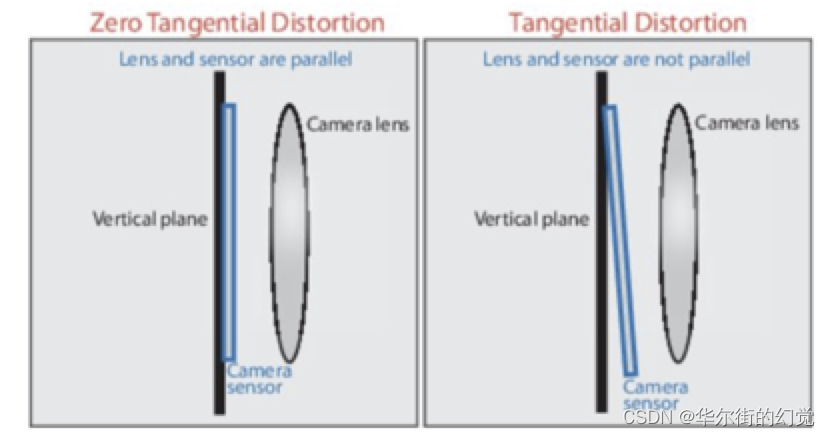畸变模型可以⽤两个额外的参数p1和p2来描述：
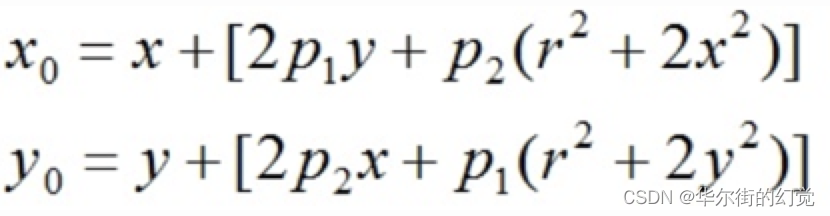下图显示某个透镜的切向畸变示意图，⼤体上畸变位移相对于左下—右上⻆的连线是对称的，这跟凸透镜与传感器之间的夹⻆有关：
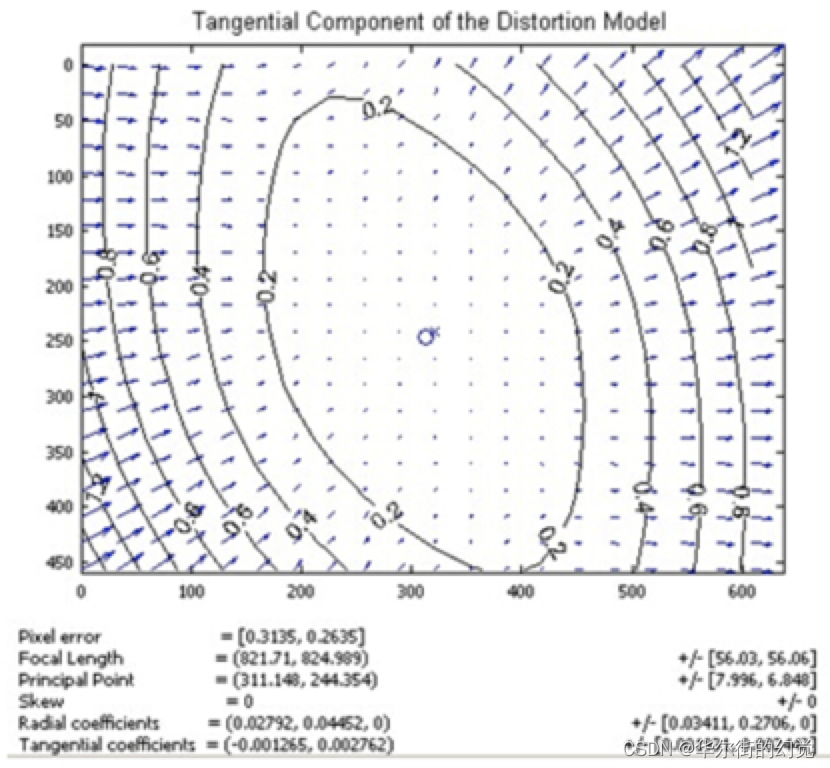
径向畸变和切向畸变模型中⼀共有5个畸变参数：k1、k2、p1、p2、k3，得到这五个参数，就可以进⾏图像的去畸变。这些都属于相机的内参。
4.1.5 相机标定的分类
相机标定方法一般分为三类，分为传统的标定算法，自标定法和基于主动视觉的标定法。分别介绍如下:
- 传统的标定算法（该项目用这个算法）：传统的相机标定算法就是基于标定物的相机标定算法，在进行相机标定时，要通过专门指定的标定物来完成，此类方法是利用标定物上构建的已确定的物点坐标和与之对应的图像点之间的联系，借助一些数学方法得到相机的内部和外部参数。它对标定物的要求有:标定物的特征部分与周围环境存在较大的差别，特征容易分辨且提取方便，标定物具有较高的稳定性也就是说它的特征不随着相机位置的变换产生畸变。常见模板有棋盘格，圆形，三角形等。
代表算法有Tsai标定法和直接线性变换法(DLT)等 - 自标定法：该算法不使用标定物，而是依靠图像点之间存在的关系，直接计算相机的参数。该算法只计算相机的内部参数的约束，不考虑相机系统的外部场景，所以方法灵活，应用范围较广，但是算法鲁棒性较差，只适合精度要求较低的场合。
- 基于主动视觉的标定法：该算法是控制相机做一些特定的动作，比如说平移旋转，得到多张图片，以此计算相机参数。使用比较广泛的有两类:一类是在二维空间中，让相机作两组纯平移运动，进而求解相机的参数，第二类是控制相机绕光心轴旋转，获得相机的参数。此类方法优点是算法简单，往往能够获得线性解，故鲁棒性较高，缺点是系统的成本高、实验设备昂贵、实验条件要求高，而且不适合于运动参数未知或无法控制的场合
3.1.6 张氏标定法
张氏标定法是张正友博士在1999年发表在国际顶级会议ICCV上的论文《FlexibleCamera Calibration By Viewing a Plane From Unknown Orientations》中，提出的一种利用平面棋盘格进行相机标定的实用方法。
该方法介于传统标定法和自标定法之间，既克服了传统标定法需要的高精度三维标定物的缺点，又解决了自标定法鲁棒性差的难题。标定过程不需要特殊的标定物只需使用一张打印出来的棋盘格，并从不同方向拍摄几组图片即可，不仅实用灵活方便，而且精度很高，鲁棒性好。因此很快被全世界广泛采用，极大的促进了三维计算机视觉从实验室走向真实世界的进程。
3.1.6.1 棋盘格数据
棋盘是一块由黑白方块间隔组成的标定板，我们用它来作为相机标定的标定物(从真实世界映射到数字图像内的对象)。之所以我们用棋盘作为标定物是因为平面棋盘模式更容易处理(相对于复杂的三维物体)，但与此同时，二维物体相对于三维物体会缺少一部分信息，于是我们会多次改变棋盘的方位来捕捉图像，以求获得更丰富的坐标信息。如下图所示，是相机在不同方向下拍摄的同一个棋盘图像。如下图所示：
3.1.6.2 单应性矩阵
张氏校正法是基于平面棋盘格的标定，首先我们介绍下两个平面中的单应性映射在计算机视觉中，单应性(Homography) 指从一个平面到另一个平面的投影映射，所以在标定物平面与图像平面之间存在单应性。
上文中我们已经得到了像素坐标系和世界坐标系下的坐标映射关系，因为标定物是平面，我们假设标定棋盘位于世界坐标中Z=0平面，然后进行单应性计算。化简前文中的公式有：
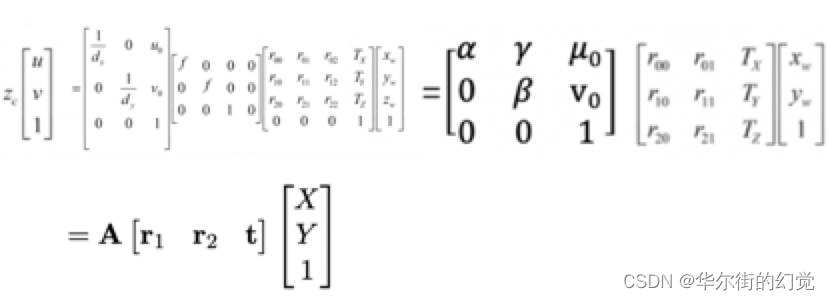
其中: u,v表示像素坐标系中的坐标，矩阵A是内参矩阵，其中a=f/dx,B=f/dy,u0,x0,Y(由于制造误差产生的两个坐标轴偏斜参数，通常很小，如果按上文中矩阵运算得到的值即为0)表示5个相机内参,r1,r2,示相机外参,xw,yw,zw 表示世界坐标系中的坐标.a,B和物理焦距f之间的关系为: a =fsx和B=fsy。其中sx=1/dx表示x方向上的1毫米长度所代表像素值，即像素/单位毫米，a,B是在相机标定中整体计算出来的。
那单应性矩阵定义为:
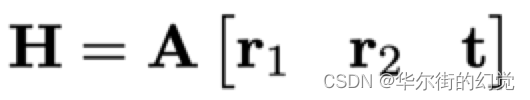代⼊上式中有：
3.1.6.3 利要约束条件求解内参矩阵
3.1.6.4 极大似然参数估计
⾸先我们回顾下极⼤似然估计：极⼤似然估计是⼀种估计总体未知参数的⽅法。它主要⽤于点估计问题。所谓点估计是指⽤⼀个估计量的观测值来估计未知参数的真值，即在参数空间中选取使得样本取得观测值的概率最⼤的参数。
3.1.7 标定流程
张氏标定就是利用一张打印的棋盘格，然后对每个角点进行标记其在像素坐标系的像素点坐标，以及在世界坐标系的坐标，张氏标定证明通过4组以上的点就可以求解出H矩阵的值，但是为了减少误差，具有更强的鲁棒性，我们一般会拍摄许多张照片，选取大量的角点进行标定。具体过程如下:
- 打印一张棋盘格标定图纸，将其贴在平面物体的表面
- 拍摄一组不同方向棋盘格的图片，可以通过移动相机来实现，也可以移动标定图片来实现。
- 对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点(角点，也就是下图中黑白棋盘交叉点，中间品红色的圆圈内就是一个角点)。我们定义打印的棋盘图纸位于世界坐标系ZW=0的平面上，世界坐标系的原点位于棋盘图纸的固定一角(比如下图中黄色点)。像素坐标系原点位于图片左上角。
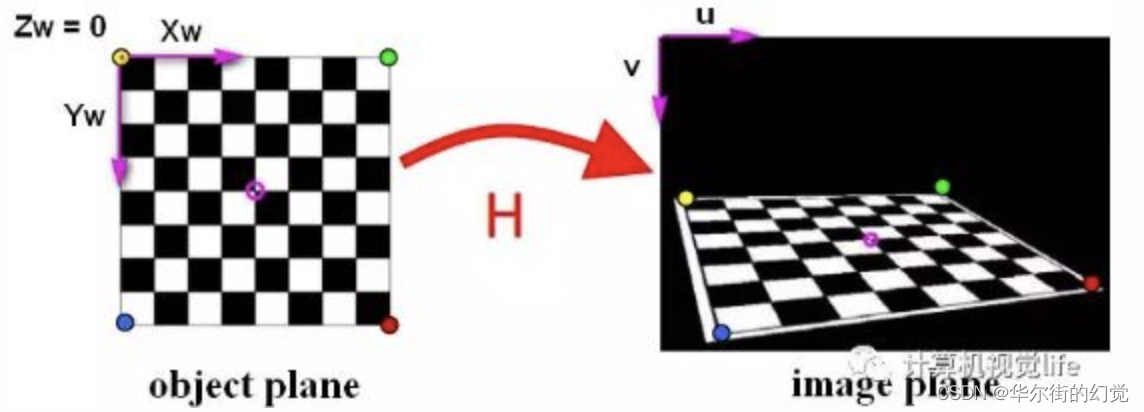
因为棋盘标定图纸中所有角点的空间坐标是已知的，这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的，如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒)，就可以根据LM等优化方法得到单应性矩阵H，进而得到相机的内参，外参等信息。
3.1.8 总结
-
相机标定的意义
建立世界坐标系和像素坐标之间的关系，可用于三维重建，图像校正等 -
成像原理
小孔成像 -
相机成像模型
- 世界坐标系:目标物体位置的参考系，是为了更好的描述相机的位置创建的
- 相机坐标系:站在相机角度的坐标系
- 图像坐标系:以图像中心为原点的坐标系
- 像素坐标系:以图像左上角为原点的坐标系
- 坐标系之间的转换：刚体变换 — 透射变换一离散化
- 内参:描述相机内部属性的参数
- 外参:决定相机坐标与世界坐标系之间相对位置关系
-
图像畸变
- 径向畸变：沿着透镜半径方向产生的畸变
- 切向畸变：透镜本身与相机传感器平面或图像平面不平行而产生
-
相机标定方法分类
传统的标定方法，自标定法，基于主动视觉的标定方法 -
张氏标定法
利用棋盘格图像对相机进行标定:单应性矩阵，利用约束条件求解内参矩阵根据内参矩阵估计外参矩阵，利用极大似然方法估计参数，优化方法:牛顿法，高斯牛顿法和LM算法标定流程:
- 打印一张棋盘格标定图纸，将其贴在平面物体的表面
- 拍摄一组不同方向棋盘格的图片，可以通过移动相机来实现，也可以移动标定图片来实现
- 对于每张拍摄的棋盘图片，检测图片中所有棋盘格的特征点
- 因为棋盘标定图纸中所有角点的空间坐标是已知的，这些角点对应在拍摄的标定图片中的角点的像素坐标也是已知的，如果我们得到这样的N>=4个匹配点对(越多计算结果越鲁棒)，就可以根据LM等优化方法得到单应性矩阵H，得到相机的内参，外参等信息。
-
双目校正
双目较正，就是利用单目校正得到每个相机的参数后，在计算两个相机之间的相对位置。
4.2 相机校正和图像校正
学习目标
- 知道相机校正API及其使用方法
- 了解图像去畸变的方法，用内参外参去畸变
4.2.1 相机标定
根据张正友校正算法，利用棋盘格数据校正对车载相机进行校正，计算其内参矩阵，外参矩阵和畸变系数。
标定的流程是：
- 准备棋盘格数据，即用于标定的图片
- 对每一张图片提取角点信息
- 在棋盘上绘制提取到的角点(非必须，只是为了显示结果)
- 利用提取的角点对相机进行标定
- 获取相机的参数信息
4.2.1.1 标定的图片
标定的图片需要使用棋盘格数据在不同位置、不同角度、不同姿态下拍摄的图片最少需要3张，当然多多益善，通常是10-20张。该项目中我们使用了20张图片，如下图所示：
把这些图⽚存放在项⽬路径中的camera_cal⽂件夹中。
4.2.1.2 相机校正
下⾯我们对相机进⾏校正，OPenCV中提供了对相机进⾏校正的代码，在本项⽬中直接使⽤opencv中的API进⾏相机的校正，如下所示：
# 1. 参数设定:定义棋盘横向和纵向的⻆点个数并指定校正图像的位置
nx = 9
ny = 6
file_paths = glob.glob("./camera_cal/calibration*.jpg")
# 2. 计算相机的内外参数及畸变系数
def cal_calibrate_params(file_paths):
object_points = [] # 三维空间中的点：3D
image_points = [] # 图像空间中的点：2d
# 2.1 ⽣成真实的交点坐标：类似(0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)的三维点
objp = np.zeros((nx * ny, 3), np.float32)
objp[:, :2] = np.mgrid[0:nx, 0:ny].T.reshape(-1, 2)
# 2.2 检测每幅图像⻆点坐标
for file_path in file_paths:
img = cv2.imread(file_path)
# 将图像转换为灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# ⾃动检测棋盘格内4个棋盘格的⻆点（2⽩2⿊的交点）
rect, corners = cv2.findChessboardCorners(gray, (nx, ny), None)
# 若检测到⻆点，则将其存储到object_points和image_points
if rect == True:
object_points.append(objp)
image_points.append(corners)
# 2.3 获取相机参数
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(object_points, image_points, gray.shape[::-1], None, None)
return ret, mtx, dist, rvecs, tvecs
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
在这⾥有⼏个API给⼤家介绍下：
-
寻找棋盘图中的棋盘⻆点
rect, corners = cv2.findChessboardCorners(image, pattern_size, flags)- 1
参数:
- Image:输入的棋盘图，必须是8位的灰度或者彩色图像
- Pattern size:棋盘图中每行每列的角点个数(内角点)
- flags:用来定义额外的滤波步骤以有助于寻找棋盘角点。所有的变量都可以单独或者以逻辑或的方式组合使用。取值主要有:
- CV_CALIB CB ADAPTIVE THRESH:使用自适应值(通过平均图像亮度计算得到)将图像转换为黑白图，而不是一个固定的阈值
- CV_CALIB CB NORMALIZE IMAGE:在利用固定值或者自适应的值进行二值化之前，先使用cvNormalizeHist来均衡化图像亮度
- CV CALIB CB FILTER QUADS:使用其他的准则 (如轮廓面积，周长，方形形状)来去除在轮廓检测阶段检测到的错误方块。
返回:
- Corners:检测到的角点
- rect: 输出是否找到角点，找到角点返回1，否则返回0
-
检测完角点之后我们可以将将测到的角点绘制在图像上，使用的API是
cv2.drawChessboardCorners(img,pattern size, corners， rect)- 1
参数:
- Img: 预绘制检测角点的图像
- pattern size:预绘制的角点的形状
- corners:角点矩阵
- rect: 表示是否所有的棋盘角点被找到，可以设置为findChessboardCorners的返回值
注意：如果发现了所有的角点，那么角点将用不同颜色绘制(每行使用单独的颜色绘制)，并且把角点以一定顺序用线连接起来，如下图所示
-
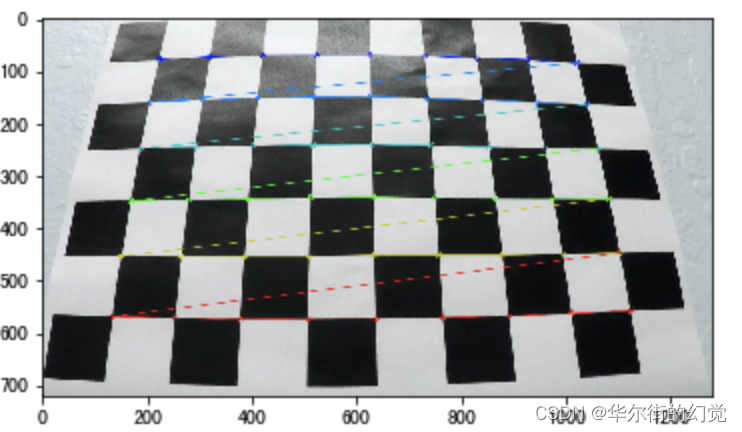
利⽤定标的结果计算内外参数
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(object_points, image_points- 1
参数:
- Object_points:世界坐标系中的点，在使用棋盘的场合，我们令z的坐标值为0，而x,y坐标用里面来度量，选用英寸单位，那么所有参数计算的结果也是用英寸表示。最简单的方式是我们定义棋盘的每一个方块为一个单位
- image points:在图像中寻找到的角点的坐标，包含object points所提供的所有
- iimage size:图像的大小，以像素为衡量单位
返回:
- ret: 返回值
- mtx相机的内参矩阵，大小为3x3的矩阵
- dist:畸变系数，为5*1大小的矢量
- rvecs: 旋转变量
- tvecs: 平移变量
4.2.1.2 图像去畸变
上⼀步中我们已经得到相机的内参及畸变系数，我们利⽤其进⾏图像的去畸变，最直接的⽅法就是调⽤opencv中的函数得到去畸变的图像：
def img_undistort(img, mtx, dist):
dst = cv2.undistort(img, mtx, dist, None, mtx)
return dst
- 1
- 2
- 3
我们看下求畸变的API:
dst = cv2.undistort(img, mtx, dist, None, mtx)
- 1
参数：
- Img: 要进⾏校正的图像
- mtx: 相机的内参
- dist: 相机的畸变系数
返回： - dst: 图像校正后的结果
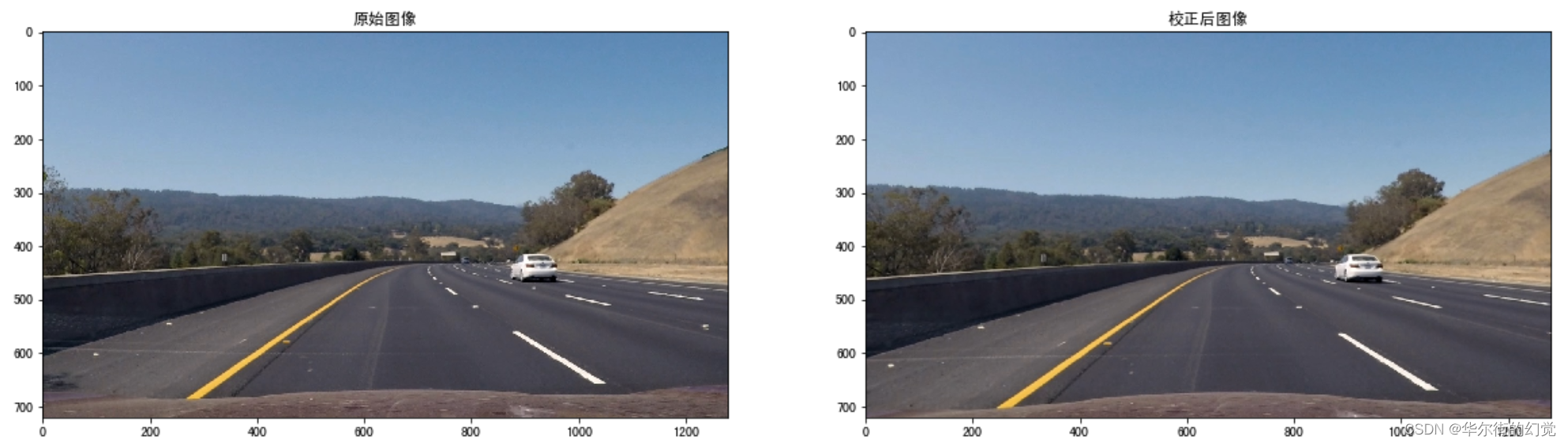
4.2.1.3 总结
- 标定的图片
不同角度和方向拍摄的棋盘格图片数据 - 相机校正
检测棋盘格数据的角点：cv2.findChessboardCorners
计算相机的内参数和外参数：cv2.calibrateCamera - 图像去畸变
cv2.undistort()
4.3 车道线提取
学习目标
- 了解HLS颜色空间
- 了解车道线提取的方法
我们基于图像的梯度和颜色特征，定位车道线的位置
在这里选用Sobel边缘提取算法，Sobel相比于Canny的优秀之处在于，它可以选择横向或纵向的边缘进行提取。从车道的拍摄图像可以看出，我们关心的正是车道线在横向上的边缘突变。OpenCV提供的cv2.Sobel()函数，将进行边缘提取后的图像做二进制图的转化，即提取到边缘的像素点显示为白色(值为1)，未提取到边缘的像素点显示为黑色(值为0)。由于只使用边缘检测，在有树木阴影覆盖的区域时，虽然能提取出车道线的大致轮廓，但会同时引入的噪声，给后续处理带来麻烦。所以在这里我们引入颜色阈值来解决这个问题
4.3.1 颜色空间
在车道线检测中，我们使用的是HSL颜色空间，其中H表示色相，即颜色，S表示饱和度，即颜色的纯度，L表示颜色的明亮程度
HSL的H(hue)分量，代表的是人眼所能感知的颜色范围，这些颜色分布在一个平面的色相环上，取值范围是0°到360°的圆心角，每个角度可以代表一种颜色。色相值的意义在于，我们可以在不改变光感的情况下，通过旋转色相环来改变颜色。在实际应用中，我们需要记住色相环上的六大主色，用作基本参照: 360°/0红、60°黄、120°绿、180°青、240°蓝、300°洋红，它们在色相环上按照60°圆心角的间隔排列：
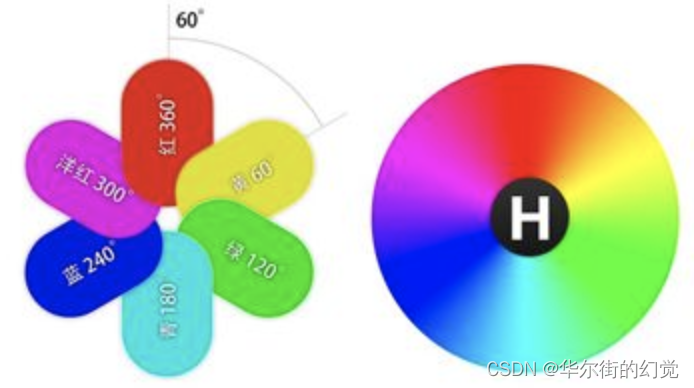HSL的S(saturation)分量，指的是⾊彩的饱和度，描述了相同⾊相、明度下⾊彩纯度的变化。数值越⼤，颜⾊中的灰⾊越少，颜⾊越鲜艳，呈现⼀种从灰度到纯⾊的变化。因为车道线是⻩⾊或⽩⾊，所以利用s通道阈值来检测车道线。
HSL的L(lightness)分量，指的是色彩的明度，作用是控制色彩的明暗变化。数值越小，色彩越暗，越接近于黑色;数值越大，色彩越亮，越接近于白色
4.3.2 车道线提取
⻋道线提取的代码如下所示：
# ⻋道线提取代码
# 颜色空间转换一》边缘检测一》颜色阈值-》合并并且使用L通道进行白的区的抑制
def pipeline(img, s_thresh=(170, 255), sx_thresh=(40, 200)):
img = np.copy(img)
#1.将图像转换为HLS⾊彩空间，并分离各个通道
hls = cv2.cvtColor(img, cv2.COLOR_RGB2HLS).astype(np.float)
h_channel = hls[:, :, 0]
l_channel = hls[:, :, 1]
s_channel = hls[:, :, 2]
#2.利⽤sobel计算x⽅向的梯度
sobelx = cv2.Sobel(l_channel, cv2.CV_64F, 1, 0)
abs_sobelx = np.absolute(sobelx)
# 将导数转换为8bit整数
scaled_sobel = np.uint8(255 * abs_sobelx / np.max(abs_sobelx))
sxbinary = np.zeros_like(scaled_sobel)
sxbinary[(scaled_sobel >= sx_thresh[0]) & (scaled_sobel <= sx_thresh[1])] = 1
# 3.对s通道进⾏阈值处理
s_binary = np.zeros_like(s_channel)
s_binary[(s_channel >= s_thresh[0]) & (s_channel <= s_thresh[1])] = 1
# 4. 将边缘检测的结果和颜⾊空间阈值的结果合并，并结合l通道的取值，确定⻋道提取的⼆值图结果
color_binary = np.zeros_like(sxbinary)
color_binary[((sxbinary == 1) | (s_binary == 1)) & (l_channel > 100)] = 1
return color_binary
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
我们来看下整个流程：
⾸先我们是把图像转换为HLS颜⾊空间，然后利⽤边缘检测和阈值的⽅法检测⻋道线，我们以下图为例，来看下检测结果：
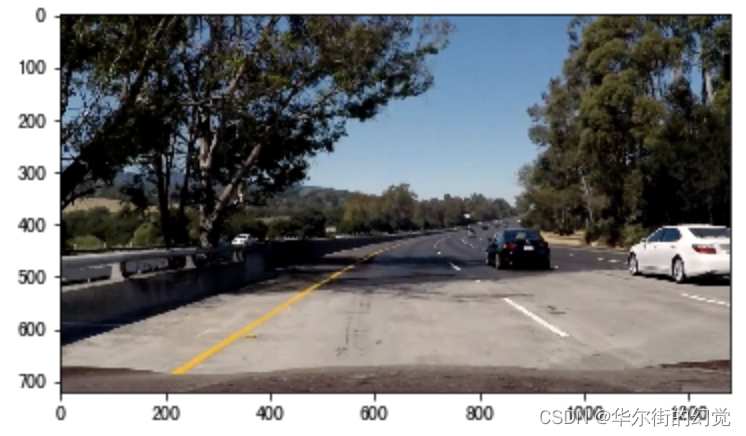
- 利⽤sobel边缘检测的结果
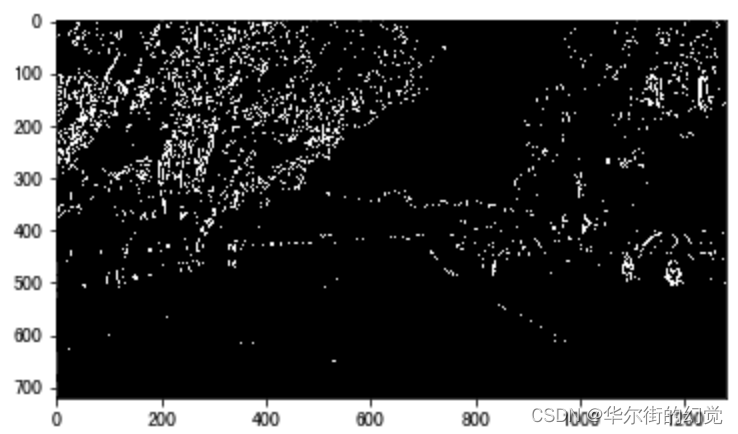
- 利⽤S通道的阈值检测结果
- 将边缘检测结果与颜⾊检测结果合并，并利⽤L通道抑制非白色的信息：
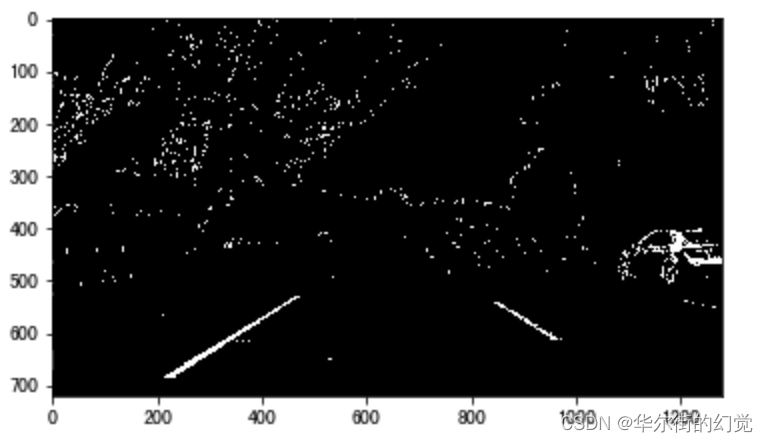
总结：
- 颜⾊空间：
HLS：⾊相，饱和度，明亮程度 - ⻋道线提取
颜⾊空间转换-》边缘检测-》颜⾊阈值-》利用L通道抑制非白色-》合并得到检测结果。
4.4 透视变换
学习⽬标
- 知道透视变换在⻋道线检测中的应⽤
为了方便后续的直方图滑窗对车道线进行准确的定位，我们在这里利用透视变换将图像转换成俯视图，也可将俯视图恢复成原有的图像，代码如下:
计算透视变换所需的参数矩阵：
def cal_perspective_params(img, points):
offset_x = 330
offset_y = 0
img_size = (img.shape[1], img.shape[0])
src = np.float32(points)
# 俯视图中四点的位置
dst = np.float32([[offset_x, offset_y], [img_size[0] - offset_x, offset_y]
[offset_x, img_size[1] - offset_y],
[img_size[0] - offset_x, img_size[1] - offset_y]
])
# 从原始图像转换为俯视图的透视变换的参数矩阵
M = cv2.getPerspectiveTransform(src, dst)
# 从俯视图转换为原始图像的透视变换参数矩阵
M_inverse = cv2.getPerspectiveTransform(dst, src)
return M, M_inverse
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
透视变换：
def img_perspect_transform(img, M):
img_size = (img.shape[1], img.shape[0])
return cv2.warpPerspective(img, M, img_size)
- 1
- 2
- 3
下面我们调用上述两个方法看下透视变换的结果:在原始图像中我们绘制道路检测的结果，然后通过透视变换转换为俯视图
img = cv2.imread("./test/straight_lines2.jpg")
img = cv2.line(img, (601, 448), (683, 448), (0, 0, 255), 3)
img = cv2.line(img, (683, 448), (1097, 717), (0, 0, 255), 3)
img = cv2.line(img, (1097, 717), (230, 717), (0, 0, 255), 3)
img = cv2.line(img, (230, 717), (601, 448), (0, 0, 255), 3)
points = [[601, 448], [683, 448], [230, 717], [1097, 717]]
M, M_inverse = cal_perspective_params(img, points)
transform_img = img_perspect_transform(img, M)
plt.figure(figsize=(20,8))
plt.subplot(1,2,1)
plt.title('原始图像')
plt.imshow(img[:,:,::-1])
plt.subplot(1,2,2)
plt.title('俯视图')
plt.imshow(transform_img[:,:,::-1])
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
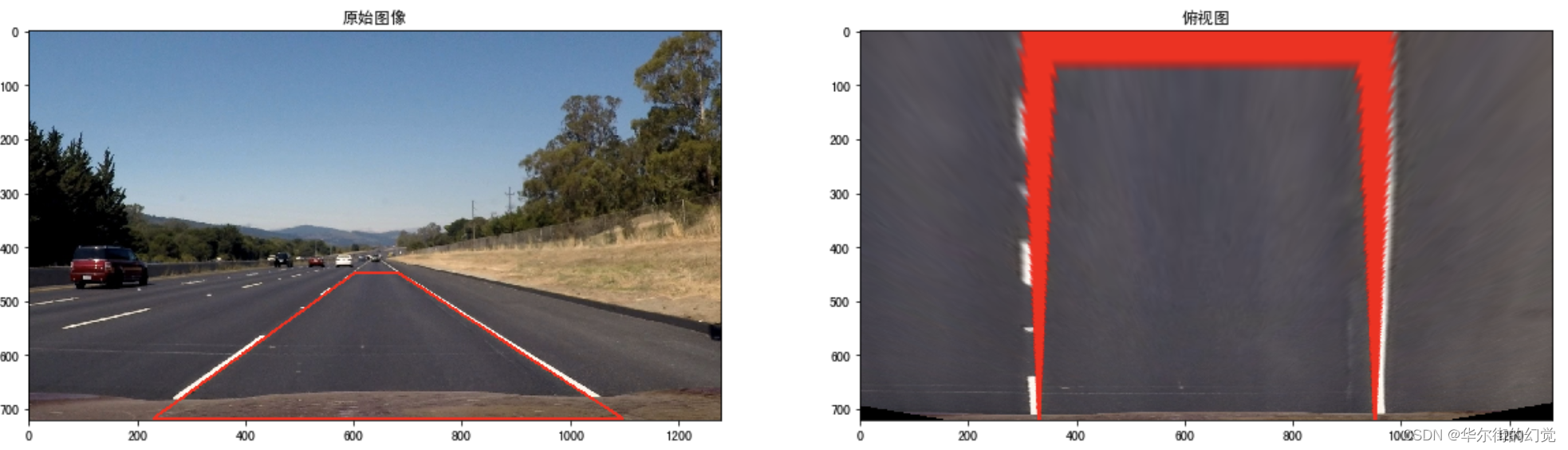
总结
透视变换将检测结果转换为俯视图。
4.5 车道线定位及拟合
学习目标
- 了解直方图确定车道线位置的思想
我们根据前面检测出的车道线信息，利用直方图和滑动窗口的方法，精确定位车道线，并进行拟合。
4.5.1 定位思想
下图是我们检测到的车道线结果
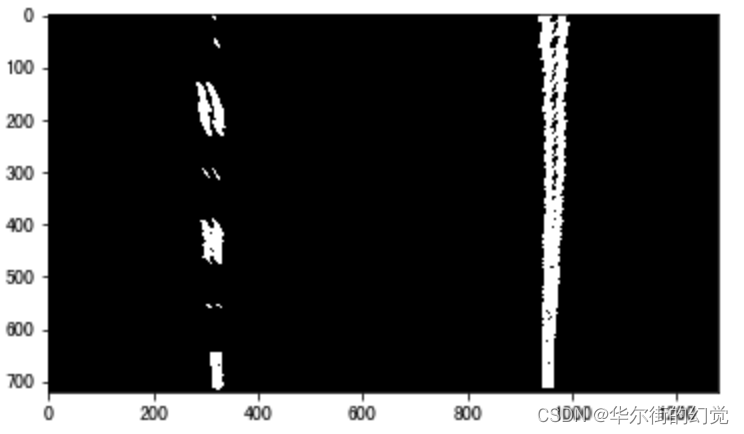
沿x轴方向统计每一列中白色像素点的个数，横坐标是图像的列数，纵坐标表示每列中白色点的数量，那么这幅图就是“直方图”，如下图所示: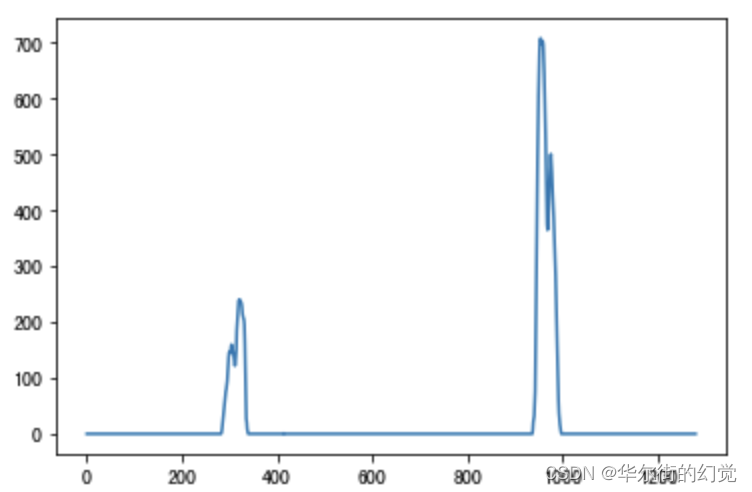
对比上述两图，可以发现直方图左半边最大值对应的列数，即为左车道线所在的位置，直方图右半边最大值对应的列数，是右车道线所在的位置。
确定左右车道线的大致位置后，使用”滑动窗口“的方法，在图中对左右车道线的点进行搜索。
滑动窗口的搜索过程：
-
设置搜索窗口大小(width和height) :一般情况下width为手工设定，height为图片大小除以设置搜索窗口数目计算得到。
-
以搜寻起始点作为当前搜索的基点，并以当前基点为中心，做一个网格化搜索。
-
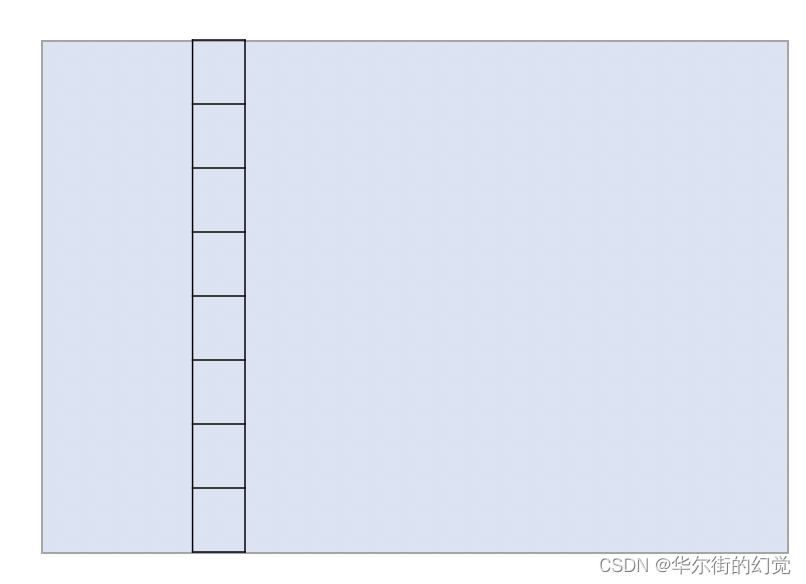
对每个搜索窗口分别做水平和垂直方向直方图统计，统计在搜索框区域内非零像素个数，并过滤掉非零像素数目小于50的框。
-
计算非零像素坐标的均值作为当前搜索框的中心，并对这些中心点做一个二阶的多项式拟合，得到当前搜寻对应的车道线曲线参数。
实现代码如下：
def cal_line_param(binary_warped):
# 1.确定左右⻋道线的位置
# 统计直⽅图
histogram = np.sum(binary_warped[:, :], axis=0)
# 在统计结果中找到左右最⼤的点的位置，作为左右⻋道检测的开始点
# 将统计结果⼀分为⼆，划分为左右两个部分，分别定位峰值位置，即为两条⻋道的搜索位置
midpoint = np.int(histogram.shape[0] / 2)
leftx_base = np.argmax(histogram[:midpoint])
rightx_base = np.argmax(histogram[midpoint:]) + midpoint
# 2.滑动窗⼝检测⻋道线
# 设置滑动窗⼝的数量，计算每⼀个窗⼝的⾼度
nwindows = 9
window_height = np.int(binary_warped.shape[0] / nwindows)
# 获取图像中不为0的点
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
# ⻋道检测的当前位置
leftx_current = leftx_base
rightx_current = rightx_base
# 设置x的检测范围，滑动窗⼝的宽度的⼀半，⼿动指定
margin = 100
# 设置最⼩像素点，阈值⽤于统计滑动窗⼝区域内的⾮零像素个数，⼩于50的窗⼝不对x的中⼼值进⾏更新
minpix = 50
# ⽤来记录搜索窗⼝中⾮零点在nonzeroy和nonzerox中的索引
left_lane_inds = []
right_lane_inds = []
# 遍历该副图像中的每⼀个窗⼝
for window in range(nwindows):
# 设置窗⼝的y的检测范围，因为图像是（⾏列）,shape[0]表示y⽅向的结果，上⾯是0
win_y_low = binary_warped.shape[0] - (window + 1) * window_height
win_y_high = binary_warped.shape[0] - window * window_height
# 左⻋道x的范围
win_xleft_low = leftx_current - margin
win_xleft_high = leftx_current + margin
# 右⻋道x的范围
win_xright_low = rightx_current - margin
win_xright_high = rightx_current + margin
# 确定⾮零点的位置x,y是否在搜索窗⼝中，将在搜索窗⼝内的x,y的索引存⼊left_lane_ind
good_left_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xleft_low) & (nonzerox < win_xleft_high)).nonzero()[0]
good_right_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xright_low) & (nonzerox < win_xright_high)).nonzero()[0]
left_lane_inds.append(good_left_inds)
right_lane_inds.append(good_right_inds)
# 如果获取的点的个数⼤于最⼩个数，则利⽤其更新滑动窗⼝在x轴的位置
if len(good_left_inds) > minpix:
leftx_current = np.int(np.mean(nonzerox[good_left_inds]))
if len(good_right_inds) > minpix:
rightx_current = np.int(np.mean(nonzerox[good_right_inds]))
# 将检测出的左右⻋道点转换为array
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
# 获取检测出的左右⻋道点在图像中的位置
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
# 3.⽤曲线拟合检测出的点,⼆次多项式拟合，返回的结果是系数
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
return left_fit, right_fit
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
⻋道线的检测的拟合结果如下图所示：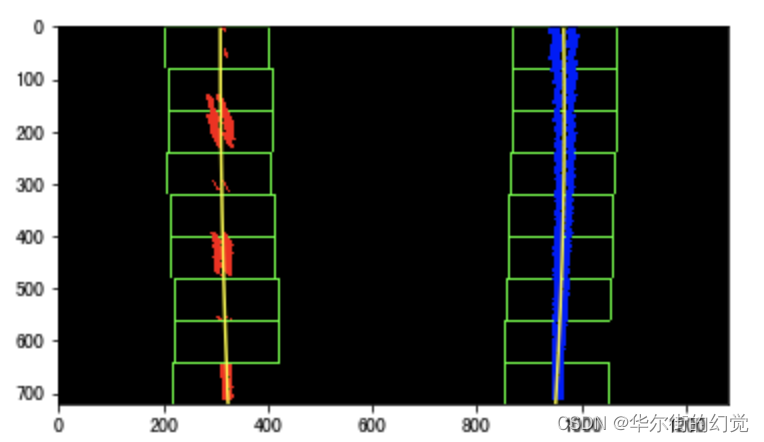
其中绿色的方框是滑动窗口的结果，中间的黄线是车道线拟合的结果下面我们将车道区域绘制处理，即在检测出的车道线中间绘制多边形，代码如下:
def fill_lane_poly(img, left_fit, right_fit):
# 获取图像的⾏数
y_max = img.shape[0]
# 设置输出图像的⼤⼩，并将⽩⾊位置设为255
out_img = np.dstack((img, img, img)) * 255
# 在拟合曲线中获取左右⻋道线的像素位置
left_points = [[left_fit[0] * y ** 2 + left_fit[1] * y + left_fit[2], y] for y in range(y_max)]
right_points = [[right_fit[0] * y ** 2 + right_fit[1] * y + right_fit[2], y] for y in range(y_max -1,-1,-1)]
# 将左右⻋道的像素点进⾏合并
line_points = np.vstack((left_points, right_points))
# 根据左右⻋道线的像素位置绘制多边形
cv2.fillPoly(out_img, np.int_([line_points]), (0, 255, 0))
return out_img
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
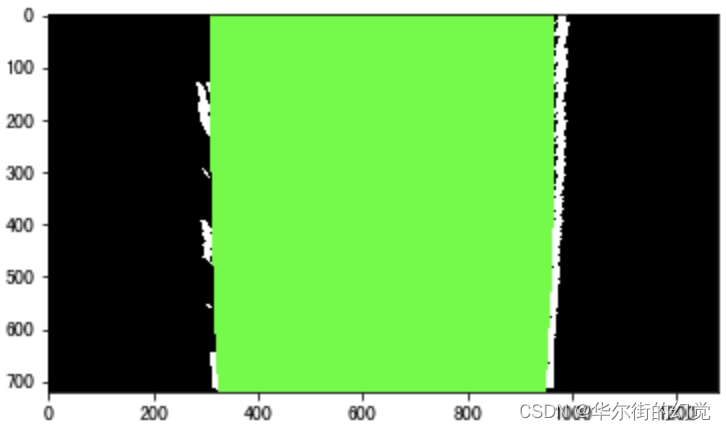
其中两个方法给大家介绍下
np.vstack:按垂直方向(行顺序) 堆叠数组构成一个新的数组np.dstack:按水平方向(列顺序) 堆叠数组构成一个新的数组
将检测出的车道逆投影到原始图像，直接调用透视变换的方法即可
transform img_inverse = img_perspect_transform(result, M inverse)
- 1
效果如下图所示
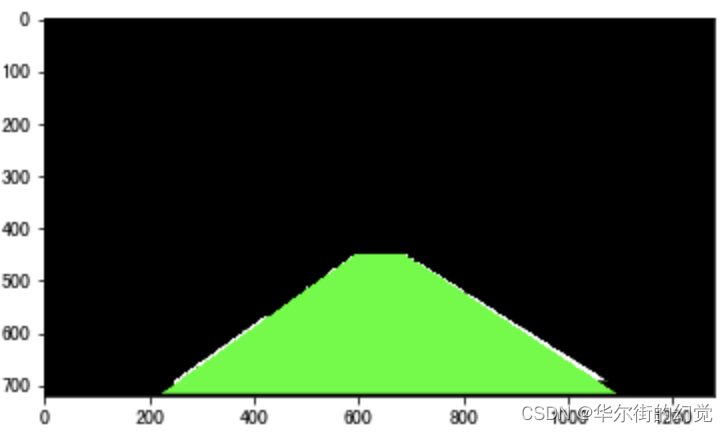
最后将其叠加在原图像上，则有：
4.6 车道曲率和中心点偏离距离计算
学习目标
- 知道车道曲率计算的方法
- 知道计算中心点偏离距离的计算
4.6.1 曲率的介绍
曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大，表示曲线的弯曲程度越大。曲率的倒数就是曲率半径
4.6.1.1 圆的曲率
下面有三个球体，网球、篮球、地球，半径越小的越容易看出是圆的，所以随着半径的增加，圆的程度就越来越弱了
我们根据上述的计算曲率半径的⽅法，代码实现如下：
def cal_radius(img, left_fit, right_fit):
# 图像中像素个数与实际中距离的⽐率
# 沿⻋⾏进的⽅向⻓度⼤概覆盖了30⽶，按照美国⾼速公路的标准，宽度为3.7⽶（经验值）
ym_per_pix = 30 / 720 # y⽅向像素个数与距离的⽐例
xm_per_pix = 3.7 / 700 # x⽅向像素个数与距离的⽐例
# 计算得到曲线上的每个点
left_y_axis = np.linspace(0, img.shape[0], img.shape[0] - 1)
left_x_axis = left_fit[0] * left_y_axis ** 2 + left_fit[1] * left_y_axis + left_fit[2]
right_y_axis = np.linspace(0, img.shape[0], img.shape[0] - 1)
right_x_axis = right_fit[0] * right_y_axis ** 2 + right_fit[1] * right_y_axis + right_fit[2]
# 获取真实环境中的曲线
left_fit_cr = np.polyfit(left_y_axis * ym_per_pix, left_x_axis * xm_per_pix,2)
right_fit_cr = np.polyfit(right_y_axis * ym_per_pix, right_x_axis * xm_per_pix,2)
# 获得真实环境中的曲线曲率
left_curverad = ((1 + (2 * left_fit_cr[0] * left_y_axis * ym_per_pix + left_fit_cr[1])**2)**1.5) \
/np.absolute(2 * left_fit_cr[0])
right_curverad = ((1 + (2 * right_fit_cr[0] * right_y_axis * ym_per_pix + right_fit_cr[1])**2)**1.5) \
/np.absolute(2 * right_fit_cr[0])
# 在图像上显示曲率
cv2.putText(img, 'Radius of Curvature = {}(m)'.format(np.mean(left_curverad)),(20,50),cv2.FONT_ITALIC,1,
(255, 255, 255), 5)
return img
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
显示效果：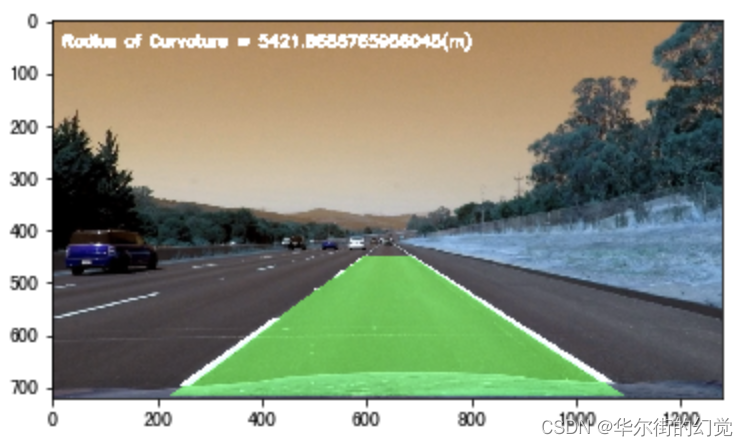
计算偏离中⼼的距离：
# 1. 定义函数计算图像的中⼼点位置
def cal_line__center(img):
undistort_img = img_undistort(img, mtx, dist)
rigin_pipline_img = pipeline(undistort_img)
transform_img = img_perspect_transform(rigin_pipline_img, M)
left_fit, right_fit = cal_line_param(transform_img)
y_max = img.shape[0]
left_x = left_fit[0] * y_max ** 2 + left_fit[1] * y_max + left_fit[2]
right_x = right_fit[0] * y_max ** 2 + right_fit[1] * y_max + right_fit[2]
return (left_x + right_x) / 2
# 2. 假设straight_lines2_line.jpg，这张图⽚是位于⻋道的中央，实际情况可以根据测量验证.
img =cv2.imread("./test/straight_lines2_line.jpg")
lane_center = cal_line__center(img)
print("⻋道的中⼼点为：{}".format(lane_center))
# 3. 计算偏离中⼼的距离
def cal_center_departure(img, left_fit, right_fit):
# 计算中⼼点
y_max = img.shape[0]
left_x = left_fit[0] * y_max ** 2 + left_fit[1] * y_max + left_fit[2]
right_x = right_fit[0] * y_max ** 2 + right_fit[1] * y_max + right_fit[2]
xm_per_pix = 3.7 / 700
center_depart = ((left_x + right_x) / 2 - lane_center) * xm_per_pix
# 在图像上显示偏移
if center_depart > 0:
cv2.putText(img, 'Vehicle is {}m right of center'.format(center_depart),(20,100),
(255, 255, 255), 5)
elif center_depart < 0:
cv2.putText(img, 'Vehicle is {}m left of center'.format(-center_depart),(20,100),
(255, 255, 255), 5)
else:
cv2.putText(img, 'Vehicle is in the center', (20, 100), cv2.FONT_ITALIC,1,(255,255,255))
return img
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
显示效果如下：
总结
- 曲率是表示曲线的弯曲程度，在这里是计算车道的弯曲程度
- 偏离中心的距离：利用已知的在中心的图像计算其他图像的偏离距离
