使用Verilog语言实现三-八译码器与八位全加器_用if语句和case语句描述3:8译码器

【1】三-八译码器

（1）三八译码器真值表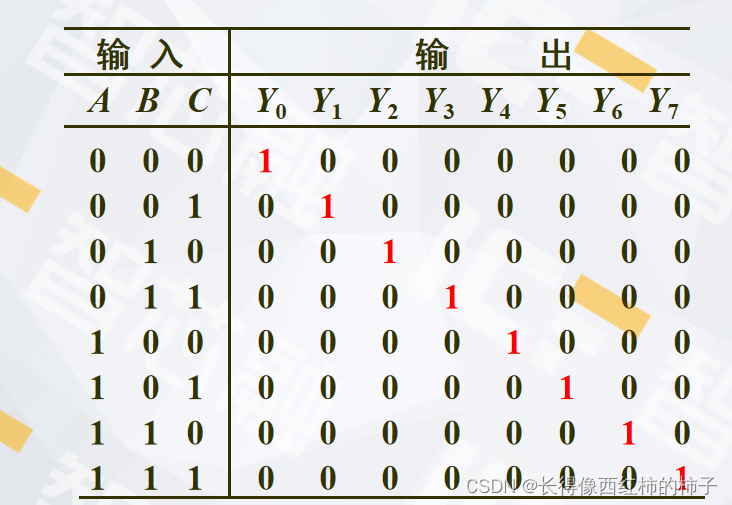

 这张真值表看着复杂，其实采用条件判断语句就能轻松解决，但也得用到“{}”的知识，例如“{}”可以将多个二进制数组合成一个，下面的方法也要用到。

（2）if..else语法

module _38(
input wire a,b,c,
output reg [7:0] out
);
always@(*)
 if({a, b, c}==3'b000)
 out=8'b0000_0001;
 else if( {a, b, c} ==3'b001)
 out=8'b0000_0010;
 else if( {a, b, c} ==3'b010)
 out=8'b0000_0100;
 else if( {a, b, c} ==3'b011)
 out=8'b0000_1000;
 else if( {a, b, c} ==3'b100)
 out=8'b0001_0000;
 else if( {a, b, c} ==3'b101)
 out=8'b0010_0000;
 else if( {a, b, c} ==3'b110)
 out=8'b0100_0000;
 else if( {a, b, c} ==3'b111)
 out=8'b1000_0000;
endmodule

 以上的是。

（3）case语法

module _38(
input wire a,b,c,
output reg [7:0] out
);
always@(*)
case({a,b,c})
    3'b000: out=8'b0000_0001;
	 3'b001: out=8'b0000_0010;
	 3'b010: out=8'b0000_0100;
	 3'b011: out=8'b0000_1000;
	 3'b100: out=8'b0001_0000;
	 3'b101: out=8'b0010_0000;
	 3'b110: out=8'b0100_0000;
	 3'b111: out=8'b1000_0000;
endcase
endmodule

 以上的是。

【2】八位全加器

（1）一位全加器

实现一位全加器有很多种方法，例如门电路法；不过我们这儿采用简化法，用自己对电路的了解来写代码。

module one_add(
input a,b,c,
output wire ben,jin
);
assign ben=a^b^c;
assign jin=(a&b)|(a&c)|(b&c);
endmodule

其中的“ben”是全加器中的本位，“jin”是全加器中的进位，“a,b,c”是三个输入。 

（2）模块使用

用一位全加器模块组合实现八位全加器

module _8add(
input [7:0] a,b,
input cin,
output [7:0] c,
output out
);
wire [7:1] tem;
one_add (a[0],b[0],cin,c[0],tem[1]),
        (a[1],b[1],tem[1],c[1],tem[2]),
		  (a[2],b[2],tem[2],c[2],tem[3]),
		  (a[3],b[3],tem[3],c[3],tem[4]),
		  (a[4],b[4],tem[4],c[4],tem[5]),
		  (a[5],b[5],tem[5],c[5],tem[6]),
		  (a[6],b[6],tem[6],c[6],tem[7]),
		  (a[7],b[7],tem[7],c[7],out);
endmodule

“a,b”为8位二进制输入，也就是相加的俩个二进制数；“cin”为从下进位的一位二进制数；“c”为相加结果输出；“out”为相加后的一位二进制进位；“tem”是为了继承每次计算后的进位并反馈给下一次的计算。

这种方法可以大幅度减少代码的篇幅，也很容易方便理解。